Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista de la Unión Matemática Argentina
Print version ISSN 0041-6932
Rev. Unión Mat. Argent. vol.50 no.1 Bahía Blanca June 2009
Exponential families of minimally non-coordinated graphs
Francisco Soulignac* and Gabriel Sueiro
Abstract. A graph G is coordinated if, for every induced subgraph H of G, the minimum number of colors that can be assigned to the cliques of H in such a way that no two cliques with non-empty intersection receive the same color is equal to the maximum number of cliques of H with a common vertex. In a previous work, coordinated graphs were characterized by minimal forbidden induced subgraphs within some classes of graphs. In this note, we present families of minimally non-coordinated graphs whose cardinality grows exponentially on the number of vertices and edges. Furthermore, we describe some ideas to generate similar families. Based on these results, it seems difficult to find a general characterization of coordinated graphs by minimal forbidden induced subgraphs.
* Partially supported by UBACyT Grant X184, Argentina and CNPq under PROSUL project Proc. 490333/2004-4, Brazil.
Let 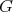 be a graph, with vertex set
be a graph, with vertex set  and edge set
and edge set  . Denote by
. Denote by 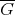 the complement of
the complement of  . Given two graphs
. Given two graphs 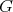 and
and 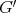 we say that
we say that 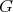 contains
contains 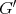 if
if 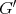 is isomorphic to an induced subgraph of
is isomorphic to an induced subgraph of 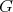 . If
. If  , we denote by
, we denote by 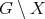 the subgraph of
the subgraph of 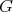 induced by
induced by 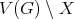 .
.
A complete set or just a complete of 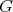 is a subset of vertices pairwise adjacent. A clique is a complete set not properly contained in any other. We may also use the term clique to refer to the corresponding complete subgraph. Let
is a subset of vertices pairwise adjacent. A clique is a complete set not properly contained in any other. We may also use the term clique to refer to the corresponding complete subgraph. Let  and
and 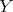 be two sets of vertices of
be two sets of vertices of  . We say that
. We say that 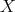 is complete to
is complete to 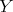 if every vertex in
if every vertex in  is adjacent to every vertex in
is adjacent to every vertex in  , and that
, and that 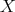 is anticomplete to
is anticomplete to 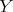 if no vertex of
if no vertex of  is adjacent to a vertex of
is adjacent to a vertex of  . A complete of three vertices is called a triangle.
. A complete of three vertices is called a triangle.
The neighborhood of a vertex  is the set
is the set 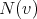 consisting of all the vertices which are adjacent to
consisting of all the vertices which are adjacent to  . The closed neighborhood of
. The closed neighborhood of  is
is ![N [v] = N (v) ∪ {v }](/img/revistas/ruma/v50n1/1a0938x.png) . A vertex of
. A vertex of 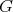 is simplicial if
is simplicial if 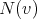 is a complete. Equivalently, a vertex is simplicial if it belongs to only one clique.
is a complete. Equivalently, a vertex is simplicial if it belongs to only one clique.
Given a graph 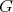 , we will denote by
, we will denote by  the set of cliques of
the set of cliques of 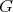 . Also, for every
. Also, for every 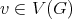 , we will denote by
, we will denote by  the set of cliques containing
the set of cliques containing  . Finally, define
. Finally, define 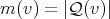 .
.
The chromatic number of a graph 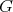 is the smallest number of colors that can be assigned to the vertices of
is the smallest number of colors that can be assigned to the vertices of 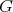 in such a way that no two adjacent vertices receive the same color, and is denoted by
in such a way that no two adjacent vertices receive the same color, and is denoted by 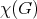 . An obvious lower bound is the maximum cardinality of the cliques of
. An obvious lower bound is the maximum cardinality of the cliques of  , the clique number of
, the clique number of  , denoted by
, denoted by 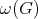 .
.
A graph  is perfect if
is perfect if  for every induced subgraph
for every induced subgraph 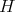 of
of  . Perfect graphs were defined by Berge in 1960 [1] and are interesting from an algorithmic point of view: while determining the chromatic number and the clique number of a graph are NP-hard problems, they are solvable in polynomial time for perfect graphs [8].
. Perfect graphs were defined by Berge in 1960 [1] and are interesting from an algorithmic point of view: while determining the chromatic number and the clique number of a graph are NP-hard problems, they are solvable in polynomial time for perfect graphs [8].
A hole is a chordless cycle of length at least  . An antihole is the complement of a hole. A hole or antihole is said to be odd if it consists of an odd number of vertices.
. An antihole is the complement of a hole. A hole or antihole is said to be odd if it consists of an odd number of vertices.
Given a graph 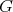 , the clique graph
, the clique graph 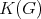 of
of 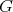 is the intersection graph of the cliques of
is the intersection graph of the cliques of 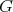 . A K-coloring of a graph
. A K-coloring of a graph  is an assignment of colors to the cliques of
is an assignment of colors to the cliques of  such that no two cliques with non-empty intersection receive the same color (equivalently, a K-coloring is a coloring of
such that no two cliques with non-empty intersection receive the same color (equivalently, a K-coloring is a coloring of 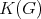 ). A Helly K-complete of a graph
). A Helly K-complete of a graph 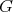 is a collection of cliques of
is a collection of cliques of 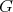 with common intersection. A Helly K-clique is a maximal Helly K-complete. The K-chromatic number and Helly K-clique number of
with common intersection. A Helly K-clique is a maximal Helly K-complete. The K-chromatic number and Helly K-clique number of  , denoted by
, denoted by  and
and 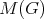 , are the sizes of a minimum K-coloring and a maximum Helly K-clique of
, are the sizes of a minimum K-coloring and a maximum Helly K-clique of 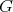 , respectively. It is easy to see by definition that
, respectively. It is easy to see by definition that 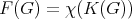 and that
and that  . Also,
. Also,  for any graph
for any graph 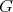 . A graph
. A graph  is coordinated if
is coordinated if 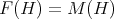 for every induced subgraph
for every induced subgraph 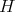 of
of 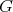 . Coordinated graphs were defined and studied in [3]. There are three main open problems concerning this class of graphs:
. Coordinated graphs were defined and studied in [3]. There are three main open problems concerning this class of graphs:
(i) find all minimal forbidden induced subgraphs for the class of coordinated graphs,
(ii) determine the computational complexity of finding the parameters  and
and 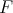 for coordinated graphs and/or some of their subclasses, and
for coordinated graphs and/or some of their subclasses, and
(iii) is there a polynomial time recognition algorithm for the class of coordinated graphs?
Recently, in [2] and [4], questions (i) and (ii) were answered partially. For question (iii), it is shown in [9] that the problem is NP-hard and it is NP-complete even when restricted to a subclass of graphs with 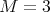 . In this note, we answer a question related to these problems, which is: how many minimally non-coordinated graphs with
. In this note, we answer a question related to these problems, which is: how many minimally non-coordinated graphs with 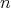 vertices and
vertices and  are there? In particular, we show (algorithmic) operations for generating a family
are there? In particular, we show (algorithmic) operations for generating a family 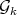 of minimally non-coordinated graphs, of size
of minimally non-coordinated graphs, of size 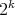 , such that every graph of the family has
, such that every graph of the family has 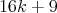 vertices and
vertices and 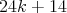 edges, for every
edges, for every  . It is not difficult to see that the operations we give are not enough for generating every minimally non-coordinated graph with
. It is not difficult to see that the operations we give are not enough for generating every minimally non-coordinated graph with  , so the question of how to generate every minimally non-coordinated graph is still open.
, so the question of how to generate every minimally non-coordinated graph is still open.
2. GENERATING NON-COORDINATED GRAPHS
It has been proved recently that perfect graphs can be characterized by two families of minimal forbidden induced subgraphs [7] and recognized in polynomial time [6].
Theorem 1 (Strong Perfect Graph Theorem [7]). Let  be a graph. Then the following are equivalent:
be a graph. Then the following are equivalent:
(i) no induced subgraph of 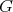 is an odd hole or an odd antihole.
is an odd hole or an odd antihole.
(ii)  is perfect.
is perfect.
Coordinated graphs are a subclass of perfect graphs [3]. Moreover, 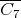 ,
, 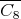 ,
,  ,
,  are minimally non-coordinated [3, 5]. Therefore,
are minimally non-coordinated [3, 5]. Therefore,  is not coordinated for all
is not coordinated for all 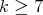 .
.
In [2, 4] and manuscript [5], partial characterizations of coordinated graphs by minimal forbidden induced subgraphs were found. In these partial characterizations, the families of minimal forbidden induced subgraphs with 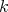 vertices have
vertices have 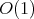 size for every
size for every  . Another partial characterization which is not difficult to prove (see [9] for a sharper result) is the following.
. Another partial characterization which is not difficult to prove (see [9] for a sharper result) is the following.
Theorem 2. Let 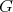 be a graph such that
be a graph such that  . Then the following are equivalent:
. Then the following are equivalent:
(i)  is perfect.
is perfect.
(ii)  does not contain odd holes.
does not contain odd holes.
(iii) 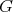 is coordinated.
is coordinated.
Corollary 3. Let 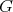 be a graph with
be a graph with  . Then
. Then 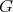 is coordinated if and only if
is coordinated if and only if 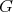 does not contain odd holes and
does not contain odd holes and  .
.
The aim of this note is to show, for every 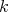 , a family of minimally non-coordinated graph of size
, a family of minimally non-coordinated graph of size  such that every graph has
such that every graph has 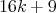 vertices and
vertices and 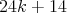 edges. In order to define our families, we are going to use exchanger and preserver graphs which were defined in [9].
edges. In order to define our families, we are going to use exchanger and preserver graphs which were defined in [9].
A graph  exchanges colors between two different vertices
exchanges colors between two different vertices  , or simply
, or simply  is an exchanger between
is an exchanger between 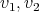 , if
, if  satisfies the following conditions:
satisfies the following conditions:
(i) No induced subgraph of  is an odd hole.
is an odd hole.
(ii)  .
.
(iii)  .
.
(iv) Every induced path between  has odd length.
has odd length.
(v) In any 3-K-coloring of  the cliques of
the cliques of  are colored with the three colors.
are colored with the three colors.
Vertices  and
and  are called connectors. Call redundant to every simplicial vertex
are called connectors. Call redundant to every simplicial vertex 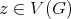 such that
such that 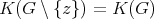 . We say that an exchanger
. We say that an exchanger  is a minimal exchanger if and only if
is a minimal exchanger if and only if  does not satisfy condition (v) for every non-redundant vertex
does not satisfy condition (v) for every non-redundant vertex  (although this is not the standard way to define minimality, this minimality is useful for "joining"
(although this is not the standard way to define minimality, this minimality is useful for "joining"  with other graphs, because redundant vertices of
with other graphs, because redundant vertices of 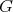 may be needed so that the cliques of
may be needed so that the cliques of 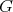 are also cliques of the joined graph). Please note that conditions (i) and (iv) are hereditary and that if
are also cliques of the joined graph). Please note that conditions (i) and (iv) are hereditary and that if 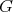 satisfies (i) and (ii) but
satisfies (i) and (ii) but 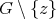 does not satisfy (ii) then, by Theorem 2 ,
does not satisfy (ii) then, by Theorem 2 , 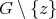 does not satisfy (v).
does not satisfy (v).
A graph 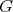 preserves colors between a set of distinct vertices
preserves colors between a set of distinct vertices  , or simply
, or simply  is a preserver between
is a preserver between  , if
, if 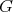 satisfies the following conditions:
satisfies the following conditions:
(i) No induced subgraph of  is an odd hole.
is an odd hole.
(ii) 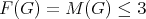 .
.
(iii)  for every
for every  .
.
(iv) Every induced path between  has odd length for all
has odd length for all 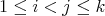 .
.
(v) In any 3-K-coloring of 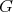 the cliques of
the cliques of 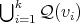 are colored with only one color.
are colored with only one color.
Vertices  are called connectors. We say that a preserver
are called connectors. We say that a preserver 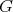 is a minimal preserver if and only if
is a minimal preserver if and only if 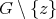 does not satisfy condition (v) for every non-redundant vertex
does not satisfy condition (v) for every non-redundant vertex  . Please note that conditions (i), (ii) and (iv) are hereditary and that condition (v) is satisfied only if condition (iii) is also satisfied.
. Please note that conditions (i), (ii) and (iv) are hereditary and that condition (v) is satisfied only if condition (iii) is also satisfied.
Let 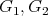 be two graphs (
be two graphs ( may be non-empty). The graph
may be non-empty). The graph 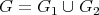 has vertex set
has vertex set  and edge set
and edge set 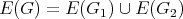 .
.
We say that graphs  are compatible when
are compatible when 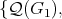


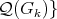 is a partition of
is a partition of 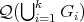 . We call them minimally compatible if they are compatible and
. We call them minimally compatible if they are compatible and 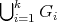 contains no redundant vertices.
contains no redundant vertices.
Theorem 4. Let 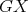 be an exchanger between
be an exchanger between  and
and  be a preserver between
be a preserver between  such that
such that 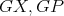 are compatible and
are compatible and 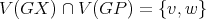 . Then
. Then 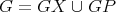 is non-coordinated. Moreover, if both
is non-coordinated. Moreover, if both 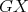 and
and 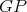 are minimal and minimally compatible then
are minimal and minimally compatible then 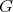 is minimally non-coordinated.
is minimally non-coordinated.
Proof. Since 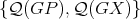 is a partition of
is a partition of 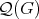 and
and 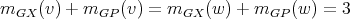 by definition, then it follows that
by definition, then it follows that 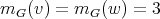 ,
, 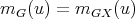 for every
for every  and
and  for every
for every 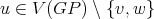 . Consequently,
. Consequently,  .
.
Suppose, contrary to our claim, that 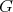 is coordinated. Then, there exists a
is coordinated. Then, there exists a 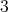 -K-coloring
-K-coloring 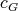 of
of 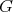 . Since the cliques of
. Since the cliques of 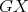 are also cliques of
are also cliques of 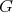 , then the K-coloring
, then the K-coloring 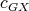 obtained by restricting the domain of
obtained by restricting the domain of  to the cliques of
to the cliques of 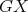 is a
is a 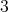 -K-coloring of
-K-coloring of 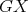 . Analogously, define
. Analogously, define 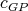 which is a
which is a  -K-coloring of
-K-coloring of 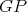 . Since
. Since 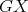 is an exchanger then there exist cliques
is an exchanger then there exist cliques  such that
such that 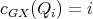 for
for  where, w.l.o.g.,
where, w.l.o.g., 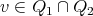 and
and 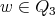 . Also, since
. Also, since 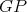 is a preserver, there exist cliques
is a preserver, there exist cliques  such that
such that 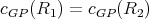 where
where 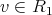 and
and 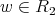 . Therefore,
. Therefore, 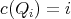 for
for 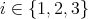 and
and 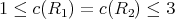 which is a contradiction because
which is a contradiction because 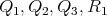 and
and 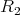 are pairwise different,
are pairwise different,  and
and 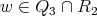 . Consequently,
. Consequently,  is a non-coordinated graph.
is a non-coordinated graph.
From now on, suppose that  and
and  are both minimal and minimally compatible. Let us see that
are both minimal and minimally compatible. Let us see that  contains no odd hole. On the contrary, suppose
contains no odd hole. On the contrary, suppose 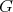 contains an odd hole
contains an odd hole 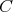 . Since neither
. Since neither 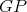 nor
nor 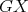 contains odd holes and
contains odd holes and 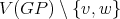 is anticomplete to
is anticomplete to 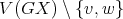 , then it follows that
, then it follows that  can be partitioned into two paths
can be partitioned into two paths 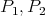 from
from  to
to  with disjoint interior and such that
with disjoint interior and such that 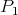 is an induced path of
is an induced path of 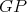 and
and  is an induced path of
is an induced path of 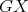 . But this is impossible, because every induced path between
. But this is impossible, because every induced path between  and
and  has odd length in both
has odd length in both  and
and  , by definition.
, by definition.
Let 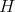 be any proper induced subgraph of
be any proper induced subgraph of 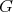 ; we have to prove that
; we have to prove that  . Since
. Since  contains no odd hole then, by Corollary 3, if
contains no odd hole then, by Corollary 3, if 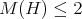 it follows that
it follows that 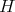 is coordinated. Thus, it suffices to prove that if
is coordinated. Thus, it suffices to prove that if  then
then 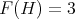 which is equivalent to prove that
which is equivalent to prove that 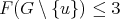 for every vertex
for every vertex 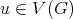 (because
(because 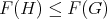 for every induced subgraph
for every induced subgraph 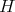 of
of 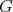 ). We divide the proof into three cases:
). We divide the proof into three cases:
Case 1:  (
( is analogous). If
is analogous). If 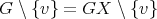 then
then  . Otherwise, let
. Otherwise, let 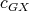 be a
be a 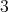 -K-coloring of
-K-coloring of  where the cliques of
where the cliques of 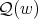 are colored using colors from the set
are colored using colors from the set 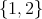 , and let
, and let 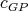 be a
be a  -K-coloring of
-K-coloring of 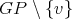 where the clique to which
where the clique to which 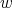 belongs has color
belongs has color 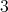 . Since
. Since 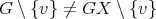 and
and 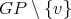 is connected it follows that the clique to which
is connected it follows that the clique to which  belongs in
belongs in 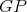 has at least one more vertex, thus it is still a clique in
has at least one more vertex, thus it is still a clique in  . Therefore
. Therefore 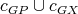 is a valid
is a valid 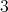 -K-coloring of
-K-coloring of 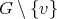 .
.
Case 2:  . Suppose first that
. Suppose first that 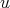 is a redundant vertex of
is a redundant vertex of 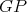 , that is,
, that is, 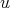 is simplicial and
is simplicial and 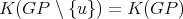 . Since
. Since 
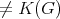 (because
(because 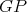 and
and 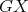 are minimally compatible) and
are minimally compatible) and  is simplicial in
is simplicial in  , then it follows that
, then it follows that 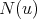 is a complete but not a clique of
is a complete but not a clique of 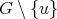 . Since
. Since  is the disjoint union of
is the disjoint union of  and
and 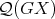 and
and 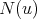 is a clique of
is a clique of 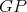 , it follows that
, it follows that  and
and 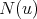 is complete in
is complete in 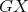 . Hence
. Hence  . Since
. Since 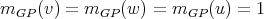 and
and  is connected, it follows that
is connected, it follows that 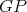 is a triangle, consequently
is a triangle, consequently 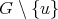

 and
and  . Now, suppose that
. Now, suppose that 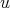 is not simplicial or
is not simplicial or 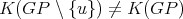 . Then,
. Then, 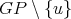 has a
has a  -K-coloring
-K-coloring 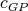 where the clique containing
where the clique containing  has color
has color 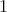 and the clique containing
and the clique containing 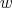 has color
has color  (because
(because 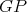 is minimal). Let
is minimal). Let  be a
be a 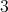 -K-coloring of
-K-coloring of 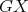 where the cliques containing
where the cliques containing  have colors
have colors 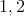 and the cliques containing
and the cliques containing 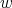 have colors
have colors  . Then
. Then 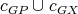 is a valid
is a valid  -K-coloring of
-K-coloring of 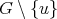 .
.
Case 3: 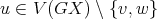 . By minimality, if
. By minimality, if 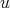 is not redundant then
is not redundant then  has a
has a 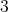 -K-coloring
-K-coloring 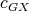 where the cliques of
where the cliques of 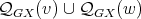 are colored with at most two colors, say
are colored with at most two colors, say 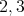 . Let
. Let  be a
be a 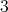 -K-coloring of
-K-coloring of  where the cliques containing
where the cliques containing  and
and  all have color
all have color  . Then
. Then 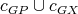 is a
is a  -K-coloring of
-K-coloring of 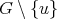 . If
. If 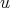 is redundant then, as before, it follows that
is redundant then, as before, it follows that ![N [u]](/img/revistas/ruma/v50n1/1a09344x.png) is the clique
is the clique 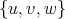 in
in 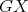 and
and 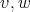 belong to a clique
belong to a clique 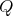 in
in  . Let
. Let 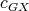 be a
be a 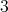 -K-coloring of
-K-coloring of 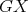 where
where 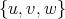 has color
has color 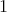 and
and 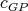 be a
be a 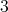 -K-coloring of
-K-coloring of  where
where  has color
has color  . Then
. Then 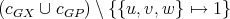 is a
is a 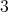 -K-coloring of
-K-coloring of 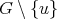 .
. 
In this section we define a recursive operator for constructing exponentially many non-isomorphic exchangers. Then we use these exchangers and one preserver to generate the exponential families, as in Section 2 . More operators for constructing exchangers and preservers are shown in the next section.
Let 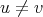 be vertices of a graph
be vertices of a graph  and
and 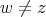 be vertices of
be vertices of 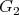 . The graph
. The graph 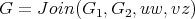 has
has 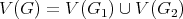 and
and  . In particular, when
. In particular, when  is an exchanger between
is an exchanger between 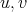 ,
, 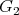 is a preserver between
is a preserver between 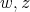 , and
, and 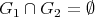 , we denote
, we denote  . Figure 2 shows examples of this operation, using graphs in Figure 1
. Figure 2 shows examples of this operation, using graphs in Figure 1

Figure 1. Preservers  and
and 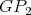 and exchanger
and exchanger 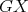 . In every graph the connectors are
. In every graph the connectors are  and
and  .
.
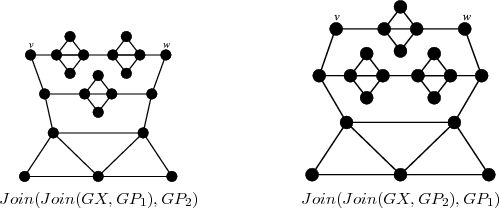
Figure 2.  and
and 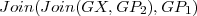 are shown. Both graphs are minimal exchangers with connectors
are shown. Both graphs are minimal exchangers with connectors  and
and 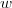 .
.
Lemma 5. Let 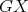 be an exchanger between
be an exchanger between 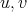 and
and 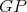 be a preserver between
be a preserver between 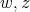 where
where 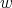 is not adjacent to
is not adjacent to  . Suppose also that
. Suppose also that 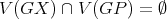 . Then
. Then  exchanges colors between
exchanges colors between 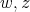 . Moreover, if both
. Moreover, if both  and
and 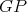 are minimal then
are minimal then 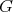 is also minimal.
is also minimal.
Proof. Arguments similar to those in Theorem 4 show that  contains no odd hole and that
contains no odd hole and that  . Also, since
. Also, since 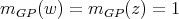 and
and 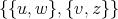 are cliques, it follows that
are cliques, it follows that  .
.
Let 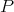 be an induced path between
be an induced path between 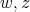 . If
. If  is also a path of
is also a path of 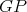 then it must have odd length. If
then it must have odd length. If  is not a path of
is not a path of  , then there must exists a subpath
, then there must exists a subpath 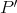 which is a path of
which is a path of 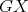 between
between 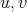 such that
such that  . Since
. Since 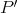 has odd length it follows that
has odd length it follows that  also has odd length.
also has odd length.
Suppose for a moment that 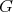 is
is 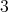 -K-colorable and let
-K-colorable and let 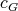 be a
be a  -K-coloring of
-K-coloring of  . Let
. Let  ,
, 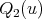 and
and 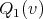 ,
, 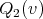 be the cliques of
be the cliques of 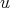 and
and  in
in 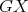 , respectively, and
, respectively, and  and
and 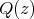 be the cliques of
be the cliques of 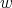 and
and  in
in 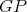 , respectively. Since
, respectively. Since 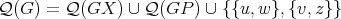 , and this union is disjoint, then it follows that the coloring
, and this union is disjoint, then it follows that the coloring 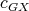 obtained by restricting the domain of
obtained by restricting the domain of 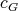 to the cliques of
to the cliques of 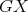 is a
is a  -K-coloring of
-K-coloring of  . Analogously, define
. Analogously, define 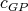 . Therefore, we may assume without loss of generality that
. Therefore, we may assume without loss of generality that 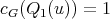 ,
,  ,
, 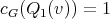 ,
, 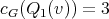 . Then
. Then 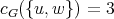 ,
,  and by definition of
and by definition of 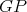 ,
, 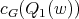

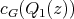
 . Hence in every 3-K-coloring of
. Hence in every 3-K-coloring of 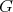 the cliques of
the cliques of 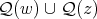 are colored with the three colors. By using the conditions derived for
are colored with the three colors. By using the conditions derived for 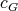 , it is easy to see that
, it is easy to see that  has at least one
has at least one 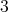 -K-coloring as supposed, thus
-K-coloring as supposed, thus  .
.
From now on, suppose  and
and 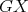 are both minimal. Let
are both minimal. Let 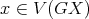 . If
. If  then
then 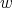 belongs to only one clique of
belongs to only one clique of 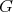 . Since
. Since 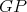 is a preserver, the clique of
is a preserver, the clique of  has the same color as one of the cliques of
has the same color as one of the cliques of  , therefore,
, therefore, 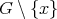 does not satisfy condition (v). The case
does not satisfy condition (v). The case  is analogous. If
is analogous. If  is redundant in
is redundant in  , then it is also redundant in
, then it is also redundant in  . If
. If 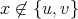 is a non-redundant vertex of
is a non-redundant vertex of 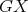 then, by minimality of
then, by minimality of 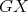 , there exists a K-coloring
, there exists a K-coloring 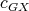 which contradicts condition (v) for
which contradicts condition (v) for  . As in Theorem 4, it is easy to combine
. As in Theorem 4, it is easy to combine 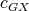 with a K-coloring of
with a K-coloring of 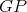 such that the coloring obtained is a K-coloring of
such that the coloring obtained is a K-coloring of 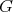 not satisfying condition (v). Similar arguments can be used to conclude the proof when
not satisfying condition (v). Similar arguments can be used to conclude the proof when 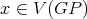 .
. 
We are now ready to show the exponential families of minimally non-coordinated graphs. Let 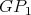 and
and 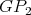 be the preserver graphs and
be the preserver graphs and  be the exchanger graph shown in Figure 1. Let
be the exchanger graph shown in Figure 1. Let 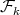 (
( ) denote the family of minimal exchangers defined by:
) denote the family of minimal exchangers defined by:
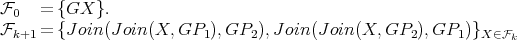
Both graphs of 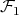 are shown in Figure 2. It is easy to see that graphs in
are shown in Figure 2. It is easy to see that graphs in  are pairwise non-isomorphic and that
are pairwise non-isomorphic and that  . Also, by construction,
. Also, by construction,  and
and 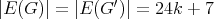 for every
for every 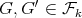 . Finally, every exchanger in
. Finally, every exchanger in 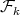 is a minimal exchanger by Lemma 5 , and is minimally compatible with
is a minimal exchanger by Lemma 5 , and is minimally compatible with 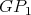 (where connectors of
(where connectors of  are identified with the connectors of the exchanger). Now, define
are identified with the connectors of the exchanger). Now, define 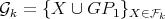 for every
for every 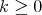 . By Theorem 4 every graph in
. By Theorem 4 every graph in 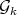 is minimally non-coordinated, that is,
is minimally non-coordinated, that is, 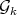 is one of the exponential families.
is one of the exponential families.
In this section we show other recursive operations for constructing exchangers and preservers. The motivation is to show how exchangers and preservers can be "joined" in a recursive manner. The proofs that these operations generate exchangers and preservers are left to the reader, and can be done in a similar way as the one in the previous section. Instead, we are going to draw sketches showing how vertices of the input graphs are tied together. The components of these sketches are shown in Figure 3 . To represent a preserver 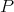 between
between 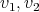 we are going to draw an oval labeled with P together with two points labeled
we are going to draw an oval labeled with P together with two points labeled 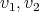 each one joined to the oval by a line. The oval represents the graph
each one joined to the oval by a line. The oval represents the graph 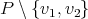 , the points represent
, the points represent  and
and 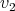 and the line between
and the line between 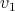 (
(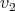 ) and the oval represents the clique of
) and the oval represents the clique of 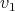 (
( ). In a similar manner, to represent an exchanger
). In a similar manner, to represent an exchanger 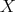 between
between 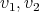 we are going to draw an oval labeled with X together with two points labeled
we are going to draw an oval labeled with X together with two points labeled  each one joined to the oval by two lines. Again, the oval represents
each one joined to the oval by two lines. Again, the oval represents 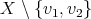 , the points represent vertices
, the points represent vertices  and the lines represent their cliques (in this case, one line of
and the lines represent their cliques (in this case, one line of 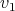 and one of
and one of  may represent the same clique). Finally, a clique with
may represent the same clique). Finally, a clique with 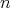 vertices is represented by an oval labeled with
vertices is represented by an oval labeled with  and
and  points outside the oval, representing each of the
points outside the oval, representing each of the 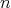 vertices. A line from one point to the oval means that the vertex belongs to the clique. Recall that a clique is a special kind of preserver, thus their vertices are also called connectors. Sometimes we also decorate the lines of the sketches with colors that represent a valid K-coloring.
vertices. A line from one point to the oval means that the vertex belongs to the clique. Recall that a clique is a special kind of preserver, thus their vertices are also called connectors. Sometimes we also decorate the lines of the sketches with colors that represent a valid K-coloring.

Figure 3. Examples of sketches. On the left there is a component for an exchanger  , in the middle there is a sketch component for a preserver
, in the middle there is a sketch component for a preserver  between
between  , and on the right there is a sketch for
, and on the right there is a sketch for 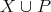 .
.
Let  be graphs which are preservers or exchangers between
be graphs which are preservers or exchangers between 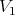 and
and 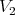 , respectively, where
, respectively, where  , and let
, and let  and
and  be sketches representing
be sketches representing  and
and 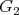 , respectively. We are going to represent the graph
, respectively. We are going to represent the graph  with a sketch formed by
with a sketch formed by  and
and 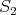 , where for every vertex
, where for every vertex  of
of 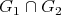 , the corresponding points of
, the corresponding points of 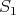 and
and 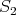 are drawn as a single point. One of such sketches is shown in Figure 3.
are drawn as a single point. One of such sketches is shown in Figure 3.
The sketches in Figure 4 represent preservers between two vertices  , the sketches in Figure 5 represent exchangers between
, the sketches in Figure 5 represent exchangers between  and the sketch in Figure 6 represents a preserver between
and the sketch in Figure 6 represents a preserver between  . If the set of graphs of a sketch
. If the set of graphs of a sketch  are minimally compatible and minimal (as preservers or exchangers) then the graph represented by
are minimally compatible and minimal (as preservers or exchangers) then the graph represented by 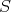 is also minimal.
is also minimal.
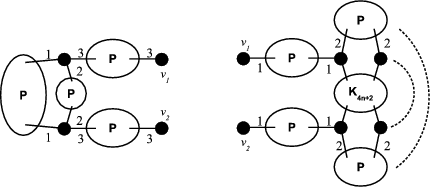
Figure 4. Two sketches of preservers between vertices 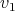 and
and 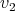 .
.
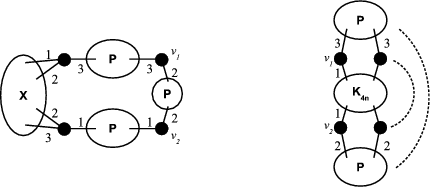
Figure 5. Two sketches of exchangers between 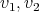 .
.
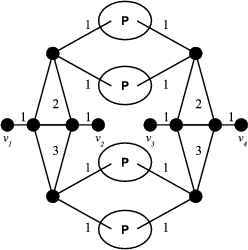
Figure 6. A sketch of a preserver between  .
.
5. CONCLUSIONS AND FURTHER REMARKS
In this note we have shown one exponential-size family of minimally non-coordinated graphs for every natural number, and several operations for building preservers and exchangers. It is not difficult to define other operations for constructing minimal preservers or exchangers in order to generate different families of minimally non-coordinated graphs. Also, adding edges to some minimally non-coordinated graph may result into another minimally non-coordinated graph. Moreover, it is not clear that preservers and exchangers are enough to define every minimally non-coordinated graph. Perhaps a set of basic graphs together with operations for generating minimally non-coordinated graphs can be defined in a more convenient way.
With all these observations it seems difficult to find a characterization of coordinated graphs by minimal forbidden induced subgraphs, even when we restrict our attention to the class of graphs with 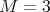 . This is in turn a complementary result to that one in [9], which states that the problem of determining whether a graph in a very restricted subclass of graphs with
. This is in turn a complementary result to that one in [9], which states that the problem of determining whether a graph in a very restricted subclass of graphs with 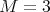 is coordinated is NP-complete.
is coordinated is NP-complete.
[1] Claude Berge. Les problèmes de coloration en théorie des graphes. Publ. Inst. Statist. Univ. Paris, 9:123-160, 1960. [ Links ]
[2] Flavia Bonomo, Maria Chudnovsky, and Guillermo Durán. Partial characterizations of clique-perfect graphs. I. Subclasses of claw-free graphs. Discrete Appl. Math., 156(7):1058-1082, 2008. [ Links ]
[3] Flavia Bonomo, Guillermo Durán, and Marina Groshaus. Coordinated graphs and clique graphs of clique-Helly perfect graphs. Util. Math., 72:175-191, 2007. [ Links ]
[4] Flavia Bonomo, Guillermo Durán, Francisco Soulignac, and Gabriel Sueiro. Partial characterizations of clique-perfect and coordinated graphs: superclasses of triangle-free graphs. Discrete Appl. Math., 2009. In press. [ Links ]
[5] Flavia Bonomo, Guillermo Durán, Francisco Soulignac, and Gabriel Sueiro. Partial characterizations of coordinated graphs: line graphs and complements of forests. Math. Methods Oper. Res., 69(2):251-270, 2009. [ Links ]
[6] Maria Chudnovsky, Gérard Cornuéjols, Xinming Liu, Paul Seymour, and Kristina Vuskovic. Recognizing Berge graphs. Combinatorica, 25(2):143-186, 2005. [ Links ]
[7] Maria Chudnovsky, Neil Robertson, Paul Seymour, and Robin Thomas. The strong perfect graph theorem. Ann. Math. (2), 164(1):51-229, 2006. [ Links ]
[8] M. Grötschel, L. Lovász, and A. Schrijver. The ellipsoid method and its consequences in combinatorial optimization. Combinatorica, 1(2):169-197, 1981. [ Links ]
[9] Francisco Soulignac and Gabriel Sueiro. Np-hardness of the recognition of coordinated graphs. Ann. Oper. Res., 169(1):17-34, 2009. [ Links ]
Francisco Soulignac
Departamento de Computación
Facultad de Ciencias Exactas y Naturales
Universidad de Buenos Aires
Ciudad de Buenos Aires, Argentina
fsoulign@dc.uba.ar
Gabriel Sueiro
Departamento de Computación
Facultad de Ciencias Exactas y Naturales
Universidad de Buenos Aires
Ciudad de Buenos Aires, Argentina
gsueiro@dc.uba.ar
Recibido: 6 de agosto de 2007
Aceptado: 10 de julio de 2008














