Serviços Personalizados
Journal
Artigo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares em
SciELO
Similares em
SciELO
Compartilhar
Revista de la Unión Matemática Argentina
versão impressa ISSN 0041-6932
Rev. Unión Mat. Argent. vol.50 no.1 Bahía Blanca jun. 2009
Weak type (1, 1) of maximal operators on metric measure spaces
Marilina Carena
Abstract. A discretization method for the study of the weak type (1, 1) for the maximal of a sequence of convolution operators on 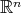 has been introduced by Miguel de Guzmán and Teresa Carrillo, by replacing the integrable functions by finite sums of Dirac deltas. Trying to extend the above mentioned result to integral operators defined on metric measure spaces, a general setting containing at once continuous, discrete and mixed contexts, a caveat comes from the result in On restricted weak type (1, 1); the discrete case (Akcoglu M.; Baxter J.; Bellow A.; Jones R., Israel J. Math. 124 (2001), 285-297). There a sequence of convolution operators in
has been introduced by Miguel de Guzmán and Teresa Carrillo, by replacing the integrable functions by finite sums of Dirac deltas. Trying to extend the above mentioned result to integral operators defined on metric measure spaces, a general setting containing at once continuous, discrete and mixed contexts, a caveat comes from the result in On restricted weak type (1, 1); the discrete case (Akcoglu M.; Baxter J.; Bellow A.; Jones R., Israel J. Math. 124 (2001), 285-297). There a sequence of convolution operators in  is constructed such that the maximal operator is of restricted weak type (1, 1), or equivalently of weak type (1, 1) over finite sums of Dirac deltas, but not of weak type (1, 1). The purpose of this note is twofold. First we prove that, in a general metric measure space with a measure that is absolutely continuous with respect to some doubling measure, the weak type (1, 1) of the maximal operator associated to a given sequence of integral operators is equivalent to the weak type (1, 1) over linear combinations of Dirac deltas with positive integer coefficients. Second, for the non-atomic case we obtain as a corollary that any of these weak type properties is equivalent to the weak type (1, 1) over finite sums of Dirac deltas supported at different points.
is constructed such that the maximal operator is of restricted weak type (1, 1), or equivalently of weak type (1, 1) over finite sums of Dirac deltas, but not of weak type (1, 1). The purpose of this note is twofold. First we prove that, in a general metric measure space with a measure that is absolutely continuous with respect to some doubling measure, the weak type (1, 1) of the maximal operator associated to a given sequence of integral operators is equivalent to the weak type (1, 1) over linear combinations of Dirac deltas with positive integer coefficients. Second, for the non-atomic case we obtain as a corollary that any of these weak type properties is equivalent to the weak type (1, 1) over finite sums of Dirac deltas supported at different points.
2000 Mathematics Subject Classification. Primary 42B25
Key words and phrases. Maximal operator; Weak type (1, 1); Dirac delta.
The author was supported by CONICET, CAI+D (UNL) and ANPCyT
The problem of determination of the weak type 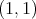 of maximal operators associated to a sequence of convolution kernels from its behavior on classes of special functions or distributions has as starting point the results of Moon in [14]. There, the weak type
of maximal operators associated to a sequence of convolution kernels from its behavior on classes of special functions or distributions has as starting point the results of Moon in [14]. There, the weak type 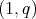 of the maximal operator associated to the convolution operators induced by a sequence of integrable kernels in
of the maximal operator associated to the convolution operators induced by a sequence of integrable kernels in 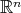 , is proved to be equivalent to the restricted weak type
, is proved to be equivalent to the restricted weak type  , with
, with  . This means that to guarantee the weak type
. This means that to guarantee the weak type  of such operator, is enough to test its action over the collection of all characteristic functions of measurable sets in
of such operator, is enough to test its action over the collection of all characteristic functions of measurable sets in 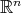 with finite measure.
with finite measure.
The next relevant step was introduced by T. Carrillo y M. de Guzmán (see [8] and [5]), where characteristic functions are substituted by Dirac deltas, again in the Euclidean space. A generalization of these results concerning the structure of the class of special functions providing the weak type 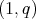 (
(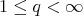 ) of such a maximal operator on
) of such a maximal operator on 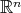 , is proved by F. Chiarenza and A. Villani in [6]. Later on, in [13], T. Menárguez y F. Soria showed how to applied the discrete approach to obtain the best constants for the weak type of maximal operator, which for the Hardy-Littlewood maximal operator is finally achieved by Melas in [10]. Extensions to weighted inequalities and for non convolution integral operators in
, is proved by F. Chiarenza and A. Villani in [6]. Later on, in [13], T. Menárguez y F. Soria showed how to applied the discrete approach to obtain the best constants for the weak type of maximal operator, which for the Hardy-Littlewood maximal operator is finally achieved by Melas in [10]. Extensions to weighted inequalities and for non convolution integral operators in  are proved by T. Menárguez (see [11] and [12]). Let us also mention some recent results by J. Aldaz and J. Varona in [4], where Dirac deltas are substituted by more general measures for convolution type operators.
are proved by T. Menárguez (see [11] and [12]). Let us also mention some recent results by J. Aldaz and J. Varona in [4], where Dirac deltas are substituted by more general measures for convolution type operators.
A natural question, taking into account the recent developments of real and harmonic analysis on metric spaces, is whether or not these results can be extended to a metric measure space, for example to a space of homogeneous type or even to non doubling settings.
Being the integers with the restriction of the usual distance and with the counting measure a space of homogeneous type, the remarkable example given by Akcoglu, Baxter, Bellow and Jones in [3] gives us the answer to our general aim: no, it is not posible to deduce the weak type of a maximal of a sequence of convolution operators on  from its weak type on Dirac deltas.
from its weak type on Dirac deltas.
These facts together leads us to at least two problems. First, if we consider non atomic metric measure spaces and sequences of integral operators with continuous kernels, we ask for the natural extension of the result in [5]. Second, in a general context containing at once discrete, continuous and mixed situations, look for small classes of functions which are enough in order to test the weak type 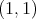 of such a maximal operator. Actually we shall solve the first problem as a corollary of our approach to the second one.
of such a maximal operator. Actually we shall solve the first problem as a corollary of our approach to the second one.
We would like to mention that the main tool for our proof is the dyadic analysis on spaces of homogeneous type started by Christ in [7].
The paper is organized as follows. In Section 2 we introduce the geometric setting and the basic properties of the dyadic families introduced by M. Christ in [7]. In Section 3 we introduce the basic properties of the kernels defining the sequence of integral operators and we state and prove the main results of this paper.
2. Dyadic sets on spaces of homogeneous type
In this section we introduce the geometric setting and we remind some properties of the "dyadic cubes" constructed by Christ. Even when the results hold on quasi-metric spaces, a theorem due to Macías an Segovia (see [9]) allows us to work on a metric setting. Let 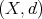 be a metric space and let
be a metric space and let 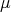 be a positive Borel measure on
be a positive Borel measure on 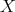 . We shall say that
. We shall say that 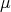 is regular on
is regular on 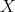 if
if
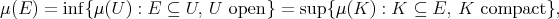
for every Borel subset  of
of 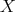 . The measure
. The measure  satisfies the doubling property on
satisfies the doubling property on  if there exists a constant
if there exists a constant  such that the inequalities
such that the inequalities

hold for every 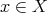 and every
and every 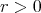 , where
, where 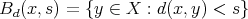 . We shall say that a metric measure space
. We shall say that a metric measure space  is a space of homogeneous type if
is a space of homogeneous type if  is a regular measure satisfying the doubling property on
is a regular measure satisfying the doubling property on  . Then if
. Then if 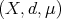 is a space of homogeneous type, the set of all the continuous functions on
is a space of homogeneous type, the set of all the continuous functions on 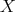 with compact support is dense in
with compact support is dense in 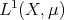 . Notice that if
. Notice that if  is a complete metric space and
is a complete metric space and 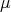 is a finite doubling measure on
is a finite doubling measure on  , then
, then 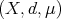 is a space of homogeneous type (see [1]).
is a space of homogeneous type (see [1]).
Given  a space of homogeneous type, let us state as a theorem the main properties of the dyadic families constructed by M. Christ in [7]. For
a space of homogeneous type, let us state as a theorem the main properties of the dyadic families constructed by M. Christ in [7]. For 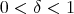 , and for each
, and for each  let
let  be a maximal
be a maximal 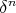 -disperse subset of
-disperse subset of 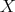 , where
, where 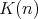 is an initial interval of natural numbers that may coincide with
is an initial interval of natural numbers that may coincide with  , and
, and  is finite for every
is finite for every 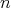 if and only if
if and only if 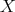 is bounded. Set
is bounded. Set 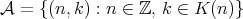 .
.
Theorem 1 (Christ). Let 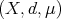 be a space of homogeneous type. Then there exist
be a space of homogeneous type. Then there exist  ,
, 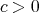 ,
, 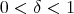 , and a family
, and a family 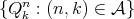 of subsets of
of subsets of 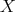 satisfying the following properties.
satisfying the following properties.
For the proof see [7] and [2]. Let us write 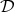 to denote the class of all "dyadic sets"
to denote the class of all "dyadic sets"  in the above theorem, i.e.
in the above theorem, i.e.

As already mentioned, in a space of homogeneous type the set of all the continuous functions with compact support is dense in 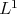 . This fact allows to prove that in this case the set of all linear combinations of characteristic functions of dyadic sets is also dense in
. This fact allows to prove that in this case the set of all linear combinations of characteristic functions of dyadic sets is also dense in  , which will be essential in the proof of the main result of this paper.
, which will be essential in the proof of the main result of this paper.
Let us start by introducing some terminology and notation. Let 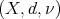 be a metric measure space, where
be a metric measure space, where  is a
is a  -finite positive Borel measure on
-finite positive Borel measure on 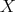 . Let us consider a sequence
. Let us consider a sequence  of kernels, where each
of kernels, where each  is a measurable function such that
is a measurable function such that  uniformly in
uniformly in  . This means that for each
. This means that for each 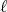 there exists
there exists  such that
such that
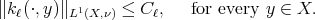
Given 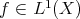 we define
we define
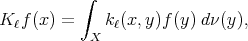
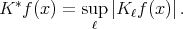
Notice that by Fubini-Tonelli's theorem, 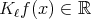 for almost every
for almost every  , and then
, and then 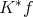 is a measurable function defined on
is a measurable function defined on 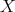 .
.
If  is a continuous function,
is a continuous function,  are different points and
are different points and  , taking
, taking
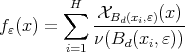
we have that

On the continuity of 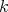 we have that
we have that 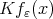 converges to
converges to 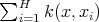 when
when  tends to zero. By the other hand,
tends to zero. By the other hand, 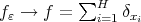 in the weak sense when
in the weak sense when  tends to zero, where
tends to zero, where 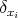 denotes the Dirac delta concentrated at the point
denotes the Dirac delta concentrated at the point  . In this sense we can consider the operator
. In this sense we can consider the operator  acting over this kind of measures
acting over this kind of measures 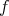 , given by
, given by
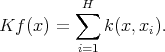
We shall say that 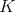 is of weak type (1,1) over finite sums of Dirac deltas (in
is of weak type (1,1) over finite sums of Dirac deltas (in  ) if there exists a constant
) if there exists a constant 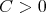 such that for each
such that for each 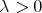 the inequality
the inequality
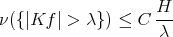
holds for every  , where
, where  are
are  different points in
different points in  .
.
Notice that 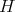 is the total variation of the measure
is the total variation of the measure 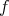 .
.
Also we shall say that the maximal operator 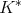 is of weak type
is of weak type  over finite sums of Dirac deltas if there exists
over finite sums of Dirac deltas if there exists 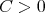 such that for every
such that for every 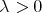 and every
and every 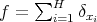 we have
we have

Let us observe that both definitions given above can be written forgetting about Dirac deltas. In particular, for the case of the maximal operator  we have that the condition
we have that the condition  for every
for every  and every
and every 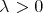 , is equivalent to say that the inequality
, is equivalent to say that the inequality
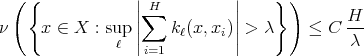
holds for every collection 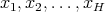 of different points in
of different points in 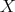 , for every
, for every 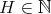 and for every
and for every 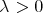 .
.
Notice finally that if each 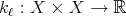 is a continuos function with compact support, Fubini-Tonelli's theorem implies that each
is a continuos function with compact support, Fubini-Tonelli's theorem implies that each 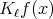 is well defined for every
is well defined for every 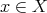 and for every
and for every 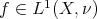 , and it is an integrable function. Moreover,
, and it is an integrable function. Moreover,  is bounded and with compact support. Then
is bounded and with compact support. Then 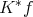 is a measurable function defined on every point of
is a measurable function defined on every point of 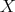 , provided that
, provided that 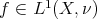 .
.
With the above definitions we are in position to state and prove the extensions of the above mentioned theorem of Miguel de Guzmán to metric measure spaces. As we already noticed, the characterization of the weak type 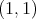 contained in that theorem is not true in general measure spaces. Actually this is the case of spaces with isolated points, even for convolution operators. In fact, K. H. Moon proves in [14] that the maximal operator associated to a sequence of convolution operators in
contained in that theorem is not true in general measure spaces. Actually this is the case of spaces with isolated points, even for convolution operators. In fact, K. H. Moon proves in [14] that the maximal operator associated to a sequence of convolution operators in 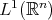 is of weak type
is of weak type 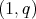 ,
, 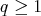 , if and only if is of restricted weak type
, if and only if is of restricted weak type  , i.e., if the weak type inequality holds for characteristic functions of sets with finite measure. A somehow surprising situation occurs when the extension of Moon's result is considered in such a simple discrete setting as is
, i.e., if the weak type inequality holds for characteristic functions of sets with finite measure. A somehow surprising situation occurs when the extension of Moon's result is considered in such a simple discrete setting as is  . In fact, in [3] the authors construct a sequence of convolution operators on
. In fact, in [3] the authors construct a sequence of convolution operators on 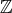 whose maximal operator is of restricted weak type
whose maximal operator is of restricted weak type 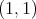 but not of weak type
but not of weak type 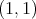 . Notice that if
. Notice that if 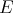 is any finite subset of
is any finite subset of 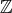 , let us say
, let us say 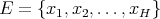 with
with 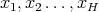 different integer numbers, we have that
different integer numbers, we have that
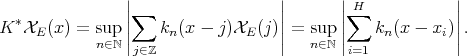
The above considerations show that a direct extension of the result of M. de Guzmán y T. Carrillo to general metric measure spaces is impossible. Nevertheless the weak type 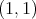 for the maximal of a given sequence of operators is equivalent to its weak type
for the maximal of a given sequence of operators is equivalent to its weak type 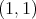 of the class of all linear combinations of Dirac deltas with positive integer coefficients. In fact our result in this direction is the following.
of the class of all linear combinations of Dirac deltas with positive integer coefficients. In fact our result in this direction is the following.
Theorem 2. Let 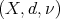 be a metric measure space, where
be a metric measure space, where  is a measure such that
is a measure such that  , with
, with 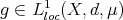 and
and 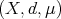 a space of homogeneous type. Let
a space of homogeneous type. Let 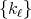 be a sequence of continuous kernels with compact support on
be a sequence of continuous kernels with compact support on  . Then
. Then 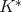 is of weak type
is of weak type 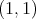 if and only if there exists a constant
if and only if there exists a constant 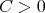 such that for every
such that for every 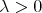 and every finite collection
and every finite collection 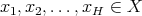 of not necessarily different points, we have
of not necessarily different points, we have
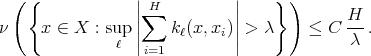
Proof. Let us start by proving that the weak type  over linear combinations of Dirac deltas with positive integer coefficients of
over linear combinations of Dirac deltas with positive integer coefficients of 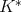 implies the weak type
implies the weak type 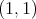 of
of 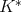 on
on 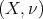 . If for a fixed natural number
. If for a fixed natural number 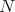 we call
we call  , then it is clear that
, then it is clear that
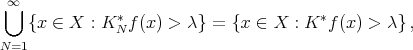
and that 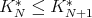 . Hence it is enough to prove that for each fixed
. Hence it is enough to prove that for each fixed 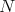 the inequality
the inequality

holds with  independent of
independent of 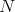 . So we take a fix
. So we take a fix 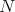 and we will show the weak type
and we will show the weak type 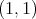 of
of 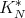 in three steps.
in three steps.
Step 1. We first prove that if  with
with 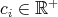 , then for every
, then for every 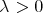 we have that
we have that
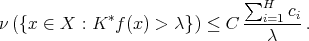
If  , we write
, we write 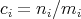 , with
, with 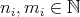 , and
, and
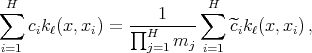
where 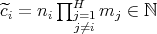 . Then, if
. Then, if  we have
we have

Now take 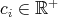 and write
and write 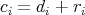 , with
, with  and
and  will be conveniently chosen later, so small as needed. Then taking
will be conveniently chosen later, so small as needed. Then taking 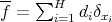 , for every
, for every  we have
we have
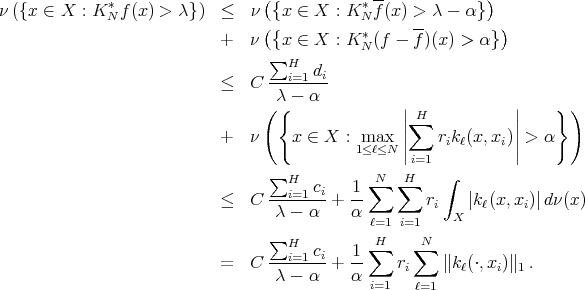
Since each  can be chosen arbitrarily small, we have
can be chosen arbitrarily small, we have
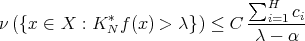
for every 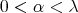 . The desired inequality follows taking limit for
. The desired inequality follows taking limit for  .
.
Step 2. We want to prove now that 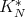 is of weak type
is of weak type 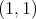 over linear combinations of characteristic functions of the dyadic sets constructed by Christ (see Section 2 ). Let
over linear combinations of characteristic functions of the dyadic sets constructed by Christ (see Section 2 ). Let  , with
, with 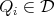 . Notice that we may assume that
. Notice that we may assume that  and that the sets
and that the sets 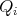 are disjoint. We want to see that for every
are disjoint. We want to see that for every 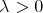 and for every function
and for every function  as above,
as above,
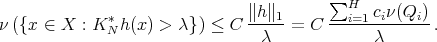
Let us observe first that if  is the given simple function, and if
is the given simple function, and if 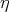 is a given positive real number, then we can write, except on a set with
is a given positive real number, then we can write, except on a set with  -measure equal to zero,
-measure equal to zero, 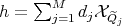 with
with  disjoint dyadic sets in
disjoint dyadic sets in 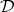 such that
such that 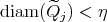 and
and 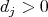 for every
for every 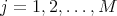 (see properties (3), (4), (6) and (8) in Theorem 1 ). Then we will keep writing
(see properties (3), (4), (6) and (8) in Theorem 1 ). Then we will keep writing 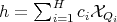 and when necessary we shall assume that the diameter of each
and when necessary we shall assume that the diameter of each 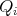 is as small as we need.
is as small as we need.
Let  where
where 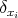 denotes the Dirac delta concentrated at
denotes the Dirac delta concentrated at 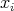 , the "center" of
, the "center" of  (see properties 2 and 3 in Theorem 1 ). For the fixed
(see properties 2 and 3 in Theorem 1 ). For the fixed  and for
and for 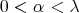 we write
we write
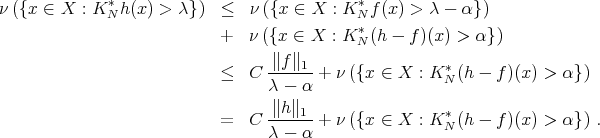
Then all we have to do is to show that the second term in the last member of the above inequalities can be made arbitrarily small by an adequate choice of the size of the dyadic sets  in the definition of the function
in the definition of the function 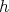 . In fact, since
. In fact, since
![| ∫ | ||∑H ∑H || |K ℓ(h - f)(x)| = || ci kℓ(x, y) d ν(y) - ciν(Qi)kℓ(x,xi)|| i=1 Qi i=1 ||∑H [∫ ∫ ]|| = || ci kℓ(x,y) dν(y) - kℓ(x,xi) dν(y) || |i=1 Qi Qi | H ∫ ∑ ≤ ci |k ℓ(x, y) - k ℓ(x,xi)| dν(y) , i=1 Qi](/img/revistas/ruma/v50n1/1a12269x.png)
we have

where  denotes the projection in the first variable of the support of
denotes the projection in the first variable of the support of 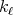 , so it is a bounded set and with finite measure. Since each
, so it is a bounded set and with finite measure. Since each 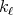 is a continuous function with compact support, given
is a continuous function with compact support, given 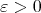 there exists
there exists  such that
such that  for every
for every 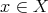 , provided that
, provided that 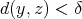 . Since we can take the diameter of each
. Since we can take the diameter of each 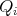 small, we conclude the proof of the Step 2.
small, we conclude the proof of the Step 2.
Step 3. From the technique of reduction to a dense subspace (see for example [8], Thm. 3.1.1) and the previous step prove we obtain the theorem in one direction.
For the converse, let us assume now that 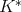 is of weak type
is of weak type 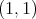 . We want to prove that
. We want to prove that 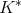 is of weak type
is of weak type  over linear combinations of Dirac deltas with positive integer coefficients. In fact, let
over linear combinations of Dirac deltas with positive integer coefficients. In fact, let 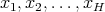 a set of different points in
a set of different points in 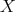 , and let
, and let  with
with  a positive integer for every
a positive integer for every  . Defining
. Defining
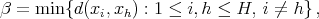
we have that  when
when  . Fix real numbers
. Fix real numbers 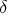 and
and  as in Christ's Theorem (Thm. 1 ), and let
as in Christ's Theorem (Thm. 1 ), and let  be a positive integer satisfying
be a positive integer satisfying 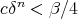 . For each
. For each 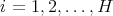 , there exists
, there exists 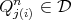 such that
such that 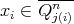 . Notice that if
. Notice that if  then
then 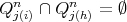 . In fact, let us suppose that there exists
. In fact, let us suppose that there exists 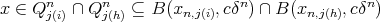 . Then
. Then
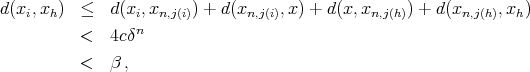
which is absurd if 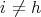 . Let us define the function
. Let us define the function  as
as

As before, fix 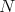 ,
, 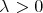 and
and  such that
such that 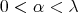 , and write
, and write
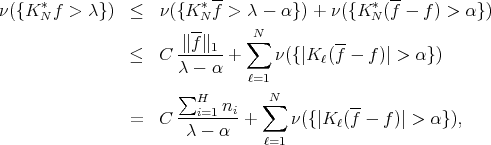
where 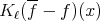 means
means
![∫ -- ∑H ni K ℓ(f - f)(x) = --(-----) n [kℓ(x,y ) - kℓ(x,xi)]dν(y ). i=1 ν Qnj(i) Qj(i)](/img/revistas/ruma/v50n1/1a12312x.png)
Hence

As in the Step 2 given 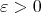 we get
we get
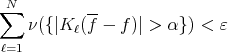
by an adequate choice for the diameter of the dyadic sets, since the each kernel  is a continuous function and we have a finite number of them. Then we have shown that
is a continuous function and we have a finite number of them. Then we have shown that
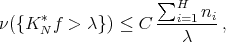
as desired.
As we already mentioned, for the non-atomic case we obtain as a corollary that the theorem of de Guzmán and Carrillo can be extended to certain metric measure spaces. More precisely, the following result state that the weak type 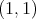 for the maximal operator of a sequence of integral operators with continuous kernels with compact support, is equivalent to the weak type
for the maximal operator of a sequence of integral operators with continuous kernels with compact support, is equivalent to the weak type 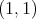 over finite sums of Dirac deltas supported at different points.
over finite sums of Dirac deltas supported at different points.
Theorem 3. Let 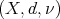 be a metric measure space without isolated points, where
be a metric measure space without isolated points, where  is a measure such that
is a measure such that 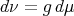 , with
, with 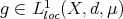 and
and  a space of homogeneous type. Let
a space of homogeneous type. Let 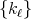 be a sequence of continuous kernels with compact support on
be a sequence of continuous kernels with compact support on 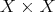 . Then
. Then 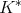 is of weak type
is of weak type 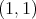 if and only if
if and only if 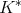 is of weak type
is of weak type 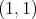 over finite sums of Dirac deltas. In other words,
over finite sums of Dirac deltas. In other words,  is of weak type
is of weak type 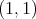 if and only if there exists a constant
if and only if there exists a constant 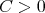 such that for every
such that for every  and every finite set
and every finite set 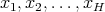 of different points in
of different points in 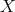 , we have
, we have
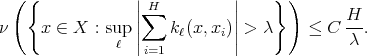
Proof. Notice that after Theorem 2 , we only have to prove that if 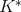 is of weak type
is of weak type  over finite sums of Dirac deltas, then it is of weak type
over finite sums of Dirac deltas, then it is of weak type 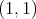 over linear combinations of Dirac deltas with positive integer coefficients. In fact, we know that there exists a constant
over linear combinations of Dirac deltas with positive integer coefficients. In fact, we know that there exists a constant 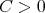 such that for every finite set
such that for every finite set  of different points and for every
of different points and for every 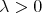 , we have
, we have

We want to see that for every finite set 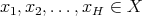 of different points and for every
of different points and for every 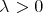 , if
, if 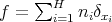 with
with 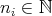 , then
, then
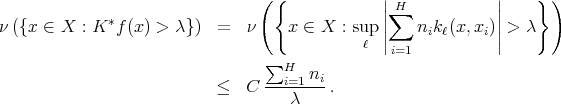
As in the proof of Theorem 2 , it will be sufficient to prove that if  is a fixed natural number, then
is a fixed natural number, then
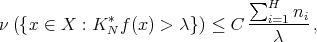
where  is independent of
is independent of 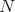 . Then let us fix
. Then let us fix 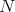 . Since
. Since 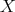 does not have isolated points, for each
does not have isolated points, for each  we can chose
we can chose 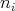 different points
different points 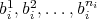 in
in 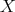 sufficiently close to
sufficiently close to  , and such that the set
, and such that the set 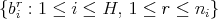 is also a collection of different points. For each fixed
is also a collection of different points. For each fixed 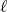 we write
we write
![∑H K ℓf(x) = nikℓ(x, xi) i=1 H n H n ∑ ∑i r ∑ ∑ i r = [k ℓ(x, xi) - kℓ(x,bi)] + kℓ(x, bi). i=1 r=1 i=1 r=1](/img/revistas/ruma/v50n1/1a12363x.png)
Hence for every  such that
such that 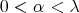 , we have
, we have
![({ | | }) * ||∑H ∑ni r || ν({x ∈ X : KN f(x) > λ}) ≤ ν x ∈ X :1m≤axℓ≤N || [kℓ(x,xi) - kℓ(x, bi)]|| > α ({ |i=1r=1 | }) ||∑H ∑ni || + ν x ∈ X : max | kℓ(x,bri)|> λ - α 1≤ ℓ≤N |i=1r=1 | = I1 + I2.](/img/revistas/ruma/v50n1/1a12366x.png)
We know that

so all we have to do is to show that given 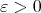 and
and  satisfying
satisfying 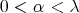 , we can chose the elements
, we can chose the elements 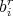 such that
such that  . In fact, let
. In fact, let
![H∑ ∑ni A ℓ(x ) = [kℓ(x,xi) - kℓ(x,bri)]. i=1 r=1](/img/revistas/ruma/v50n1/1a12373x.png)
Then

For a fixed 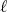 , from Chebyshev's inequality we have
, from Chebyshev's inequality we have
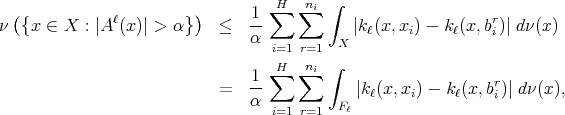
where as before 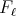 denotes the projection in the first variable of the support of
denotes the projection in the first variable of the support of  , so it is a bounded set and with finite measure. Since each
, so it is a bounded set and with finite measure. Since each 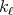 is a continuous function with compact support, given
is a continuous function with compact support, given  there exists
there exists  such that
such that 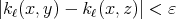 for every
for every 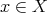 , provided that
, provided that 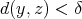 . Notice also that only a finite number of kernels
. Notice also that only a finite number of kernels 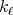 are involved, so that
are involved, so that 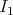 becomes small after an appropriate choice of
becomes small after an appropriate choice of 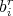 . Hence
. Hence
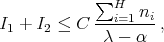
and taking  we obtain the result.
we obtain the result.
The next result of this section is devoted to relax the regularity hypothesis on 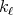 . Its proof is obtained by inspection of the proof of Theorem 2 .
. Its proof is obtained by inspection of the proof of Theorem 2 .
Theorem 4. Let 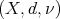 be a metric measure space, where
be a metric measure space, where  is a measure such that
is a measure such that 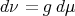 , with
, with  and
and 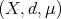 a space of homogeneous type. Let
a space of homogeneous type. Let  be a sequence of kernels such that each
be a sequence of kernels such that each 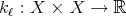 is a measurable function satisfying
is a measurable function satisfying
Then  is of weak type
is of weak type  if and only if there exists a constant
if and only if there exists a constant 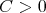 such that for every
such that for every 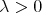 and every finite collection
and every finite collection 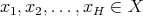 of points not necessarily different, we have
of points not necessarily different, we have
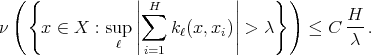
It is clear that an analogous extension of Theorem 3 can be proved.
Notice that it is possible to obtain a refined result for spaces wich are neither discrete nor purely continuous. For example, for the set

endowed with the usual distance on 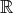 and the measure that counts on
and the measure that counts on 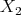 and measures lengths on
and measures lengths on  , is a space of homogeneous type (see [15]).
, is a space of homogeneous type (see [15]).
Moreover, Macías and Segovia prove in [9] that in spaces of homogeneous type the set of points with positive measure (atoms) is countable and coincides with the set of isolated points. With this characterization for the atoms we have that 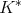 if of weak type
if of weak type 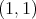 if and only if there exists a constant
if and only if there exists a constant 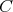 such that for every finite set
such that for every finite set 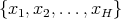 of different points in
of different points in  and for every choice of natural numbers
and for every choice of natural numbers 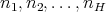 satisfying
satisfying 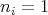 when
when 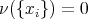 , we have that
, we have that

for every 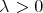 .
.
We shall finally mention that the hypotheses of the above theorems concerning continuity sometimes can be relaxed. For the basic case of Hardy-Littlewood type operator defined on a space of homogeneous type  by
by
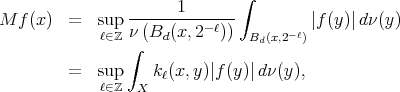
for 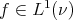 , where
, where
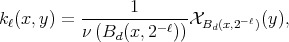
the continuity required in Theorem 2 does not hold even in Euclidean situations. On the other hand, the 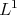 continuity required in Theorem 4 does not hold in typical spaces of homogeneous type. In fact,
continuity required in Theorem 4 does not hold in typical spaces of homogeneous type. In fact,
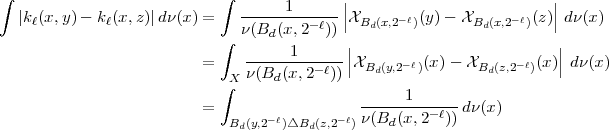 |
where  denotes the symmetric difference of the sets
denotes the symmetric difference of the sets 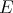 and
and 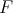 , i.e.
, i.e. 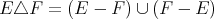 . The convergence to zero of the last integral when
. The convergence to zero of the last integral when 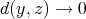 is equivalent to the convergence to zero of
is equivalent to the convergence to zero of 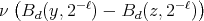 for each
for each 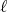 . The next example shows a non-atomic space of homogeneous type for which this property does not hold. In
. The next example shows a non-atomic space of homogeneous type for which this property does not hold. In 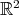 endowed with the distance
endowed with the distance 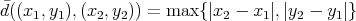 , let
, let 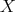 be the subset defined as
be the subset defined as

(see Figure 1) with the arc length measure 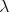 .
.

Figure 1. 
It is not difficult to see that 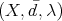 is a space of homogeneous type. Take the sequence
is a space of homogeneous type. Take the sequence  in
in  defined as
defined as 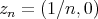 . This sequence converges to the point
. This sequence converges to the point 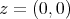 , and for each
, and for each 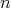 (see Figure 2), we have
(see Figure 2), we have
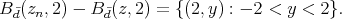

Figure 2: 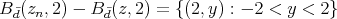
Then 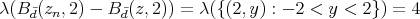 for each
for each 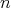 , so that
, so that 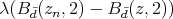 does not tend to zero when
does not tend to zero when 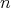 tends to infinity.
tends to infinity.
Nevertheless, the kernels 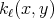 in such a general situation can be controlled by a sequence of continuous kernels. For instance consider
in such a general situation can be controlled by a sequence of continuous kernels. For instance consider
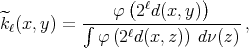
where  is the continuous function defined on the non-negative real numbers by
is the continuous function defined on the non-negative real numbers by  for every
for every  in the interval
in the interval ![[0,1 ]](/img/revistas/ruma/v50n1/1a12460x.png) ,
,  if
if  , and linear on
, and linear on ![[1,2 ]](/img/revistas/ruma/v50n1/1a12463x.png) . It is not difficult to show that each
. It is not difficult to show that each 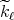 is continuous and that
is continuous and that
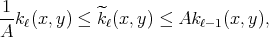
where 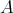 denotes the doubling constant for
denotes the doubling constant for  . Then the weak type for the maximal operator
. Then the weak type for the maximal operator 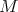 associated with the kernels
associated with the kernels 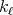 is equivalent to the weak type for the maximal operator associated with the kernels
is equivalent to the weak type for the maximal operator associated with the kernels 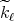 .
.
The new sequence  falls under the scope of Theorem 2 , so that the next result holds even when the kernels are not smooth.
falls under the scope of Theorem 2 , so that the next result holds even when the kernels are not smooth.
Corollary 5. Let 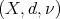 be a space of homogeneous type. Then the Hardy-Littlewood maximal function is of weak type
be a space of homogeneous type. Then the Hardy-Littlewood maximal function is of weak type 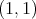 if and only if there exists a constant
if and only if there exists a constant 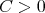 such that for every
such that for every 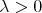 and every finite collection
and every finite collection 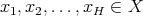 of not necessarily different points,
of not necessarily different points,
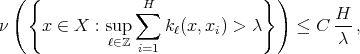
where
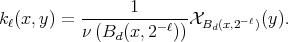
Acknowledgment. The results in this paper are part of my Doctoral Dissertation presented at the Universidad Nacional del Litoral, March 2008. I would like to express deep gratitude to my supervisors Hugo Aimar and Bibiana Iaffei for the constant support.
[1] Hugo Aimar. Distance and Measure in Analysis and PDE. Birkhäuser, Basel. Submitted for publication. [ Links ]
[2] Hugo Aimar, Ana Bernardis, and Bibiana Iaffei. Comparison of Hardy-Littlewood and dyadic maximal functions on spaces of homogeneous type. J. Math. Anal. Appl., 312(1):105-120, 2005. [ Links ]
[3] Mustafa Akcoglu, John Baxter, Alexandra Bellow, and Roger L. Jones. On restricted weak type (1, 1); the discrete case. Israel J. Math., 124:285-297, 2001. [ Links ]
[4] J. M. Aldaz and Juan L. Varona. Singular measures and convolution operators. Acta Math. Sin. (Engl. Ser.), 23(3):487-490, 2007. [ Links ]
[5] M. T. Carrillo and M. de Guzmán. Maximal convolution operators and approximations. In Functional analysis, holomorphy and approximation theory (Rio de Janeiro, 1980), volume 71 of North-Holland Math. Stud., pages 117-129. North-Holland, Amsterdam, 1982. [ Links ]
[6] Filippo Chiarenza and Alfonso Villani. Weak convergence of measures and weak type (1, q) of maximal convolution operators. Proc. Amer. Math. Soc., 97(4):609-615, 1986. [ Links ]
[7] Michael Christ. A T(b) theorem with remarks on analytic capacity and the Cauchy integral. Colloq. Math., 60/61(2):601-628, 1990. [ Links ]
[8] Miguel de Guzmán. Real variable methods in Fourier analysis, volume 46 of North-Holland Mathematics Studies. North-Holland, Amsterdam, 1981. [ Links ]
[9] Roberto A. Macías and Carlos Segovia. Lipschitz functions on spaces of homogeneous type. Adv. in Math., 33(3):257-270, 1979. [ Links ]
[10] Antonios D. Melas. The best constant for the centered Hardy-Littlewood maximal inequality. Ann. of Math. (2), 157(2):647-688, 2003. [ Links ]
[11] M. Trinidad Menárguez. On boundedness properties of certain maximal operators. Colloq. Math., 68(1):141-148, 1995. [ Links ]
[12] M. Trinidad Menárguez. Weak boundedness properties for maximal operators defined on weighted spaces. Rend. Circ. Mat. Palermo (2), 45(3):421-436, 1996. [ Links ]
[13] M. Trinidad Menárguez and Fernando Soria. Weak type (1, 1) inequalities of maximal convolution operators. Rend. Circ. Mat. Palermo (2), 41(3):342-352, 1992. [ Links ]
[14] K. H. Moon. On restricted weak type (1, 1). Proc. Amer. Math. Soc., 42:148-152, 1974. [ Links ]
[15] Liliana Nitti. Medidas que duplican y propiedades de separación métrica. Extensión de medidas con la propiedad de duplicación. Universidad Nacional del Litoral, 2003. Tesis Doctoral. [ Links ]
M. Carena
Instituto de Matemática Aplicada del Litoral (CONICET-UNL),
Departamento de Matemática(FIQ-UNL),
Universidad Nacional de Litoral,
Santa Fe, Argentina
mcarena@santafe-conicet.gov.ar
Recibido: 1 de agosto de 2008
Aceptado: 13 de octubre de 2008













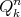 is an open subset of
is an open subset of 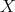 , for every
, for every 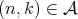 ;
;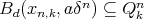 for every
for every 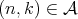 ;
;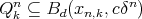 for every
for every 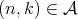 ;
; ,
, 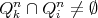 implies
implies 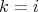 ;
; and every
and every 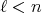 there exists a unique
there exists a unique 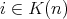 such that
such that  ;
;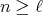 , then either
, then either 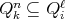 , or
, or  , for each
, for each  ,
, 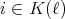 ;
;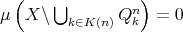 , for every
, for every 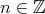 ;
;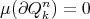 , for every
, for every 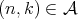 , where
, where  denotes the boundary of
denotes the boundary of 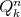 .
. , for each
, for each 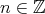 ,
,  and
and 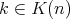 .
.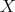 is bounded if and only if there exists
is bounded if and only if there exists 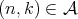 such that
such that 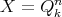 .
. 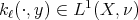 uniformly in
uniformly in 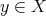 ,
,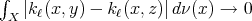 when
when  .
.
