Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Revista de la Unión Matemática Argentina
Print version ISSN 0041-6932
Rev. Unión Mat. Argent. vol.50 no.1 Bahía Blanca June 2009
Formulas for the Euler-Mascheroni constant
Pablo A. Panzone
Abstract. We give several integral representations for the Euler-Mascheroni constant using a combinatorial identity for 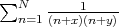 . The derivation of this combinatorial identity is done in an elemental way.
. The derivation of this combinatorial identity is done in an elemental way.
2000 Mathematics Subject Classification. 11Mxx
Key words and phrases. Euler-Mascheroni constant.
Introduction. There exist many formulas for Euler-Mascheroni constant  , see for example [7], [6]. Indeed the irrationality of
, see for example [7], [6]. Indeed the irrationality of 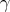 would follow from criteria given in [3] (see also [5]).
would follow from criteria given in [3] (see also [5]).
The purpose of this note is to give integral representations for 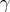 which seem to be new. As usual we write
which seem to be new. As usual we write 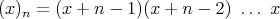 .
.
Theorem. If  ,
,  then
then
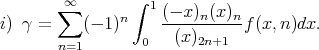

Remark 1. The formulae stated converge more rapidly than the usual definition. For example, notice that for 
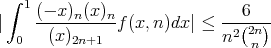
Indeed this follows form the fact that for 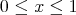 one has
one has  and
and 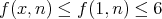 if
if  .
.
Proof. We use the following formula: if 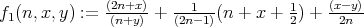 and
and  , then
, then
 | (1) |

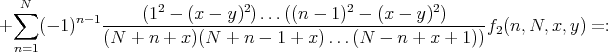

where we set 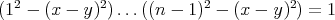 if
if 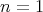 .
.
Recall the well-known representation
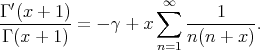 | (2) |
Notice that in (1),  as
as 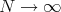 if
if 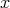 and
and 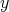 are bounded . We prove this in a moment.
are bounded . We prove this in a moment.
Now i) follows from integrating (2) from 0 to 1 and using (1) with 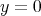 , letting
, letting 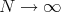 . The first formula of ii) is proved in the same way putting
. The first formula of ii) is proved in the same way putting 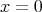 in (1).
in (1).
Now we prove (1): set  ;
;  where
where  , and define
, and define  if
if 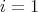 .
.
Add from 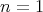 to
to 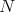 the trivial identity
the trivial identity  to get
to get
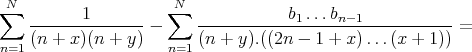
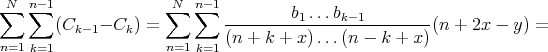 | (3) |
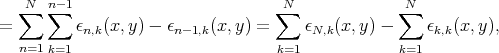
with 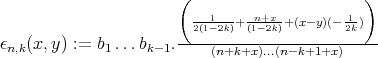 .
.
From the equality of the first expression in (3) and the last one, we obtain (1).
We now prove that if 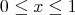 ,
, 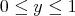 then
then 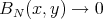 as
as  (the proof for
(the proof for 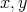 bounded is similar). Indeed in this range of
bounded is similar). Indeed in this range of 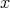 and
and 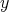 one has
one has

But 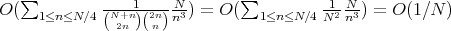 , where we have used
, where we have used  for
for 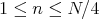 ,
, 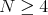 .
.
This finishes the proof of the theorem. 
A corollary of formula (1) is the following
Corollary. Let  . Set
. Set
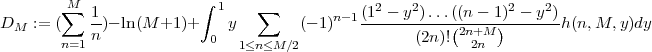
Then

Proof. From (1), letting  one gets
one gets
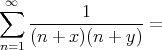

Now substitute 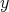 by
by 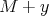 and
and  by
by  to get for
to get for 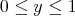
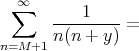
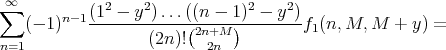
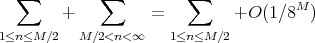
Now the corollary follows from this last formula inserted in (recall formula (2))

observing that 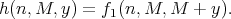

Remark 2. The corollary stated seems to give clean approximation formulas. Indeed
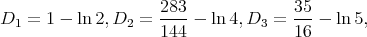
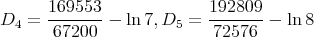
Numerically we have checked that 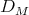 is always of the form
is always of the form 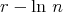 , with
, with  a rational number and
a rational number and  ,
, 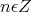 .
.
Notice that (1) or derivates of (1) give formulae for Hurwitz-Riemann's zeta function 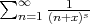 for
for  .
.
We mention without proof that formula ii) of theorem 1 is equivalent to
![∫ 1 γ = {y 3F2[1∕2,1- y,1+y; 3∕2,3∕2;- 1∕4]+ --y-- 3F2[1- y,1+y, 1+y; 3∕2,2+y;- 1∕4] 0 1 + y](/img/revistas/ruma/v50n1/1a1385x.png)
![y2 1 - ---4F3[1,1,1- y,1 + y;3∕2,2,2;- 1∕4 ]---Sinh2 (y.ArcSinh (1∕2))}dy. 4 y](/img/revistas/ruma/v50n1/1a1386x.png)
Here ![F [a ,...,a ;b ,...,b ;z] = ∑ ∞ (a1)k...(ap)k zk p q 1 p 1 q k=0 (b1)k...(bq)k k!](/img/revistas/ruma/v50n1/1a1387x.png) is the general hypergeometric function.
is the general hypergeometric function.
[1] A. J. Van der Poorten, A proof that Euler missed... Math.Intelligencer, 1 (Nr.4), 1979, 195-203. [ Links ]
[2] P. A. Panzone. Sums for Riemann's Hurwitz function II. Actas del Quinto Congreso A. Monteiro, Bahía Blanca, Universidad Nacional del Sur, 1999, 109-125. [ Links ]
[3] J. Sondow. Criteria for irrationality of Euler's Constant. Proc. Amer. Math. Soc. 131, 2003, 3335-3344. [ Links ]
[4] J. Sondow. Double integrals for Euler's constant and ln(4/p) and an analog of Hadjicostas's formula. Amer. Math. Monthly, 112, 2005, 61-65 [ Links ]
[5] J. Sondow and W. Zudilin. Euler's constant, q-logarithms, and formulas of Ramanujan and Gosper. Ramanujan J. 12, 2006, 225-244. [ Links ]
[6] X. Gourdon and P. Sebah. A collection of formulae for Euler Constant. 2003, http://numbers.computation.free.fr/Constants/Gamma/gammaFormulas.pdf. [ Links ]
[7] Eric W. Weisstein. Euler-Mascheroni Constant. From MathWorldA Wolfram Web Resource. http://mathworld.wolfram.com/Euler-MascheroniConstant.html [ Links ]
Pablo A. Panzone
Departamento e Instituto de Matemática,
Universidad Nacional del Sur,
Av. Alem 1253,
(8000) Bahía Blanca, Argentina.
ppanzone@uns.edu.ar
Recibido: 18 de octubre de 2008
Aceptado: 3 de Junio de 2009














