Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.32 n.2 Bahía Blanca abr./jun. 2002
Mass and energy balances as state-space models for aerobic batch fermentations
R. Dondo and D. Marqués
Grupo de Control de Procesos
Instituto de Desarrollo Tecnológico para la Industria Química (INTEC)
Guemes 3450 (3000) Santa Fe – Republica Argentina
e-mail: rdondo@ceride.gov.ar
Abstract — The main aim of this work is the development of mathematical models of aerobic batch fermentations for its use in estimation and control algorithms. Most batch fermentation models are empirical and simple, and do not provide interrelationships between state variables and measurements. In this work such interrelationships are obtained from mass and energy balances of the fermentation components. Since aerobic fermentations with formation of a single metabolite exhibit three degrees of freedom, three independent kinetic equations are necessary to build the state space model. Test results on the batch fermentation of xanthan gum are presented.
1. Introduction
Many publications have applied advanced control to fermentative processes carried out in continuous or fedbatch bioreactors [Wu et al. (1985); Takamatsu et al. (1985); Lim et al. (1986); San and Stephanopoulos (1986); Williams et al. (1986); Modak and Lim (1987); Agrawal et al. (1989); San and Stephanopoulos (1989); Shi et al. (1989); Harmon et al. (1989); Diener and Goldschmidt (1994); reviews by Shioya (1992) and by Shimizu (1993)]. The main obstacle for applying advanced process control to batch fermentations is the poor quality of the processes models, the relative low number of measurements, and the scarcely-known interrelationships between states and measured variables.
In batch fermentations, the main system variables can vary widely along the process. Thus, there is an opportunity for driving the manipulated variables in optimal fashion. Some publications examined the problem of determining optimal control trajectories in fermentors, considering different objective functions and control variables. Constantinides et al. (1970) presented probably the first paper that proposed the use of optimal control in batch bioreactors. Reuss (1986) presented a review on the use of optimal control in fermentative process, and only few of the reviewed works considered batch operations. In recent years, Asenjo et al. (1995) and Lee et al. (1999) presented articles on the optimal control of batch reactors, including experimental validations. In spite of the fact that trajectory optimization is a well-known technique, it has not been widely applied to fermentative processes. The reason is that optimal control results are highly dependent on the process model, and many fermentation models do not accurately represent the dynamic behavior.
Erikson et al. (1978) is one of the first publications where mass and energy balances have been used for modeling fermentations. The balances were used to derive optimal operating conditions in continuous single-cell production reactors. Roels (1980) generalized the concepts presented by Erikson et al. (1978) to other fermentations (aerobic with or without product formation and anaerobic fermentations); and outlined a scheme for building models on the basis of the available kinetic information. The relevance of macroscopic principles for modeling bioengineering systems was also discussed. Heijnen and Roels (1981) developed a slightly more complex scheme, specific to aerobic fermentations. Simple models were proposed for estimating yield coefficients on substrates with different degrees of reduction. The authors analyzed the effect of the temperature on yields and on the maintenance coefficients. Minkevich (1983) modeled the fermentation as a set of partial metabolisms, and used mass and energy balances for interrelating the partial metabolism kinetics. The influence of intracellular characteristics on the rate of physiological processes and on the culture productivity was discussed. Andrews (1989, 1993) presented a similar scheme, but with the aim of estimating macroscopic yields. Andrews (1989) discussed the limitation of yield values for the different product types.
The mentioned works show the relation between the kinetics of the intracellular processes with different levels of complexity but assuming that the intracellular reaction rates and the mass transfer mechanisms between the cells and its environment are in the steady state. Batch fermentations are time-varying processes, and we did not find any publication on the use of balances onto batch processes.
In this work, we derive a time-varying state-space model that is applicable to aerobic batch fermentations. This work is organized as follows. In section 2, statespace equations for batch fermentations are derived from a model that involves five partial metabolisms. Microscopic balances are used to calculate the relations between partial metabolisms and the net consumption of the main components. Also, macroscopic balances are used to calculate the relations between the partial metabolism rates, the variation of main component concentrations and the net flow of these components to the reactor. In section 3, these balances are combined with a simple kinetic model to derive the state space equations. In section 4, the procedure is applied to predict the evolution (consumption or production) of the gaseous components of a xanthan gum batch fermentation.
2. A state-space model for an aerobic batch fermentation
An aerobic fermentation can be seen as a set of parallel "reactions" denoted partial metabolisms. These reactions are not simple chemical reactions. The partial metabolisms either produce or consume carbon dioxide, water, oxygen, main substrate, and nitrogen source. The hydrogen involved in oxidation/reduction reactions (H+ + e-) is bound to electron carriers like NADH2 (nicotinamide adenine dinucleotides). Also, energy carriers like ATP (adenosine 5-triphosphate) transport the produced or consumed free energy.
Since fermentation models should be accurate and of the least possible complexity, the aim is to find the minimum set of differential and algebraic equations that adequately describes the process dynamics. In statespace formulation, a nonlinear model is represented by:
 | (1.a) |
| (1.b) |
where x is the state-vector, y is the vector of measurements, u is the vector of manipulated variables and p is a vector of model parameters.
In a homogeneous and constant-volume stirred-tank reactor, the balance equations are expressed as follows [Roels (1980)]:
| | (2) |
where C is a vector that represents the concentration of the main components, rC is the net conversion rate of these components, and Φ is a vector that represents the net transport rate of the system components. To be used as a state-space model, the Eq. (2) must be expressed in the form of Eq. (1). When applied to a specific fermentor, Eq. (2) provides the interrelationships between reaction rates, concentration variations, and net inlet flows. Eq. (2) represents a macroscopic balance where the microbial metabolism determines the conversion rates of the different components (rC) together with the relations between these rates. Since the microbial metabolism must obey the conservation principles, microscopic balances can be used to derive a minimum number of dynamic equations that describe the process.
In principle, microscopic balances should be applied to every fermentation component and to every element. However, considering that hundreds of components could participate in the microbial metabolism, it is necessary to limit the analysis to the so-called main components and main elements. The four main elements are C, H, O, and N, since these elements comprise about 95% of the biological mass [Roels, 1980]. The main components depend on the fermentation type, and they will be identified later for an aerobic batch fermentation with production of a single metabolite.
2.1 Microscopic balances
Figure 1 presents a model for the aerobic growth of biomass (X) using a single component as carbon and energy source (S), and an independent nitrogen source that can also contain carbon (SN). The generated metabolic component is denoted P, and CO2, H2O and O2 are components exchanged between the cells and their media. The growth is assumed to be approximately balanced, in the sense that microorganisms are able to produce exact replicas of themselves. The fermentation is modeled by five partial-metabolisms or pseudoreactions. Each pseudo-reaction is described by a stoichiometry Ei and a kinetic rate ri. This simplified description can be only explained from a stoichiometric point of view, since many biochemical reactions simultaneously participate in different partial metabolisms. The flow of main components can be subdivided according to such pseudo-reactions; and each reaction can be kinetically modeled like an integral unit [Minkevich (1983)]. This description of an aerobic fermentation, although simple, is more complete than most of the empirical models normally found in control and estimation algorithms [Constantinides et al. (1970); Wu et al. (1985); Shimizu et al.(1989)].
Fig. 1: The aerobic fermentation model as a network of partial metabolisms. (The grey boxes denote partial metabolisms that consume ATP while the white boxes denote partial metabolisms that produce ATP. The dashed arrows indicate the intracellular NADH2 flow. The continuous arrows indicate the intracellular ATP flow. The bold arrows denote exchange of main components between the biomass and its environment).
The concentration of intracellular components, ATP and NADH2, are assumed to be in the steady state [Roels (1983)]. Therefore, there is not accumulation term in their balances.
Since the element balances must be always satisfied, they represent the constraints to be met by each stoichiometry EI. The vector of main components is defined as follows:
![]()
The composition of components X, S, P, and SN is expressed by their atomic formulae CHb1Oc1Nd1, Ca2Hb2Oc2Nd2, Ca3Hb3Oc3 and Ca4Hb4Oc4Nd4 respectively (the metabolite is assumed to be a nitrogen-free component). The coefficients of the stoichiometric equations on Table 1 are expressed as the inverse of the yields (YI/J) of product I on each of the J components. The coefficients YX/ATP and YP/ATP indicate the moles of energy carriers (ATP) consumed in the anabolism and in the product metabolism respectively; and YS/ATP indicates the moles of ATP generated in the main substrate catabolism.
Table 1: Stoichiometric relations of the partial metabolisms (Ei)
The production of biomass is a process with a quantified net consumption of ATP (YX/ATP = 10.5 g X/mol ATP [Andrews (1993)]). The formation of products can either generate energy (e.g. by partial oxidation of substrates in the alcoholic fermentations) or consume energy (e.g. by generating macromolecules). The net energy demand of each reaction can be known by studying the metabolic pathways that describe the product generation [Andrews (1993)]. Apart from these processes, other numerous degradation and dissipation reactions that imply ATP consumption are also present [Minkevich (1983)]. These so-called "cellular maintenance reactions" imply a non measurable demand of ATP.
To satisfy the ATP demand for the biomass production, the metabolite production, and the cellular maintenance, a certain amount of main substrate must be oxidized. But the generated ATP (YATP/NADH2) is a function of the level of oxidative phosphorylation (P/O). This function depends on the specific metabolic oxidation pathway. Thus, the amount of oxidized main substrate must be calculated from the specific pathway function f(P/O) and from the ATP balance. The use of stoichiometric relations and balances of intracellular components (ATP and NADH2) allows to write the following relationships.
ATP balance:
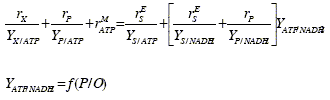 | (3) |
NADH2 balance:
 | (4) |
The consumption (or production) of main components exchanged between the cells and their media is calculated writing a mass balance for each component, as follows:
Nitrogen source consumption:
| | (5) |
Main substrate consumption:
 | (6) |
Oxygen consumption:
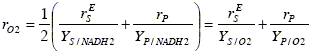 | (7) |
with YS/O2 = 2YS/NADH2; and YP/O2 = 2YP/NADH2.
Carbon dioxide production:
| | (8) |
The intracellular balances of ATP and NADH2 provide two interrelationships among the five intracellular processes. Thus, an aerobic fermentation with formation of a single metabolic product has three degrees of freedom, and the unknown rates may be obtained from the knowledge of three kinetic equations with the appropriate stoichiometric yields YI/J.
The presented model provides a fairly accurate description of an aerobic fermentation with formation of a single metabolite, and is applicable to any reactor type. However, the intracellular model parameters (P/O, rM ATP) are generally unknown and their values could change due to manipulated or non-manipulated changes in the environment.
From a macroscopic point of view and without considering intracellular components, a stoichiometry for the main substrate oxidation is obtained by adding the main substrate catabolism stoichiometry (ESE) and the oxidative phosphorilation stoichiometry for the NADH2 produced by the catabolism of the main substrate (EPO/YS/NADH2). This oxidation occurs at a rate rSE. Besides, the cellular maintenance 'reaction' consumes ATP but not main components. Thus, this reaction can be ignored in the macroscopic mass balances. For both reasons, the three independent processes that are necessary for describing the fermentation are:
• biomass growth (rX);
• metabolite production (rP); and
• main substrate oxidation (rSE).
In kinetic models of main substrate oxidation, the unknown parameters (P/O, rMATP) are usually lumped into a 'maintenance' coefficient KE that models the main substrate oxidation as a first order reaction in the biomass concentration. This assumption is common in empirical models. However, a better model for the main substrate oxidation can be obtained by reordering the ATP balance (Eq. 3), as follows:
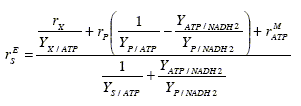 | (9) |
Since in batch reactors reaction rates rX and rP are usually time-varying, Eq. (9) shows that the main substrate oxidation is not strictly first order in the biomass concentration. Therefore, the KE parameter from a first order oxidation rate could show strong variations. In effect, when the KE coefficients of several experimental fermentations are compared [Heijnen and Roels (1981)], it is observed that their values change for similar fermentation conditions.
The assumption of a first order oxidation rate of the main substrate is only valid if the reaction rates and the mass transfer mechanisms between media and cells are in the steady state. In this case, since rX, rP, and rATPM are in the steady state and the yields are constant, then rSE is also in the steady state. However, in batch fermentations, reaction rates and mass transfer processes reach the steady state only when the metabolic activity drops to zero (i.e., at the end of the fermentation).
2.2 Macroscopic balances
The previous balance equations are independent of the kinetics and provide relationships between the rates of the different partial metabolisms and between these rates and the net consumption (or production) of main components. These relationships are also independent of the reactor type. Consider now the derivation of macroscopic relations between reaction rates, concentration of main components, and net component flows to the broth.
In aerated batch fermentors, X, P, S and SN are not transferred through the surface boundary of the vessel. Thus, the corresponding elements of the transport rate vector Φ in Eq. (2) are all zero.
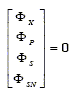 | (10) |
The oxygen concentration in the broth is considered to be in a quasi steady state because its variations are much faster than the oxygen flow transferred between the gas phase and the broth. Similarly, if the pH of the broth is constant, then the carbon dioxide concentration is also in a quasi steady state. Therefore:
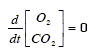 | (11) |
Thus, in aerated batch bioreactors, Eq. (2) may be written as follows:
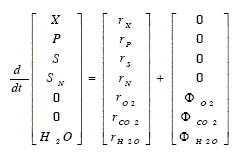 | (12) |
quation (12) indicates that the oxygen consumption rate (-rO2) and the carbon dioxide production rate (rCO2) can be obtained by measuring the oxygen transferred into the broth (-ΦO2) and the carbon dioxide transfer from the broth (ΦCO2). Except for the water, the concentration variation of the remaining main components are obtained from their formation or consumption rates.
State dynamics.
As mentioned before, rX, rP, and rSE are the three independent processes present in an aerobic fermentation with formation of a single metabolite. The dynamics of biomass growth (rX) and of metabolite production (rP) are characterized by the evolution of the biomass concentration and the metabolic product concentration. Thus, it is possible to use the following empirical equations:
 | (13) |
The main substrate oxidation is represented by:
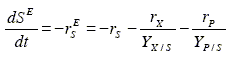 | (14) |
Note that the second equality of Eq. (14) is the Eq. (6) reordered. The state associated to this reaction is the amount of oxidized main substrate SE. Empirical expressions for rX, rP, and rS. with Eq. (14) provides the kinetics of rX, rP, and rSE and therefore complete the fermentation dynamics. Alternatively, other less usual kinetic equations together with the yields YI/J also can be used to complete the state space model.
State-measurements relations.
The theoretical relation between states and measured variables is provided by the stoichiometric coefficients. The microscopic mass balances indicate that the total consumption rate of main substrate and oxygen and the total production rate of carbon dioxide are the sum of their respective evolutions in rX, rP, and rSE (Eqs. 6, 7 and 8). The measurement of ΦO2 and ΦCO2 provides more information on the fermentation rates than on the states. Thus, it is preferable to use the cumulative oxygen consumption (∆O2(t)) and the cumulative carbon dioxide production (∆CO2(t)) at time t as measurement variables:
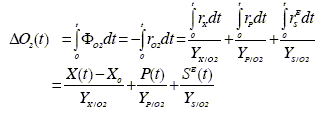 | (15.a) |
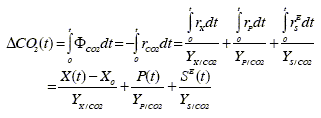 | (15.b) |
In these equations, the yield coefficients are extracted from the stoichiometric relations presented in Table 1. The yields of biomass on the other components can be exactly known only in pure cultures of a perfectly identified biomass. Therefore, their values are in general approximate, and can be estimated using some fermentation regularities, element balances and the knowledge of the broth composition [Erikson et al. (1978)].
If the main substrate and the nitrogen source concentrations are measurable, then the following equations provide relationships between the states and the two mentioned main components:
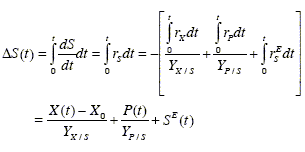 | (16.a) |
 | (16.b) |
In these expressions, X(t)-X0, P(t), and SE(t) are respectively the amounts of produced biomass, of produced metabolite, and of oxidized main substrate at time t.
Note that when the measured variables belong to the set of main components, then the stoichiometric yields allow to find linear relations between measured variables and state-variables.
2.3 Effect of the control variables and modeling of uncertainties
Batch fermentation models present the following peculiarities:
• The influence of intensive variables (pH, temperature) on the fermentation dynamics is usually expressed as empirical functions π(u) that show the dependence of the kinetic parameters π on such variables. If the intensive variables can be manipulated, then they can be used as control variables, but in this case important deviations from the empirical functions π(u) are to be expected.
• Large changes in the control variables may cause unpredictable changes in the kinetic parameters and even a variation in the structure of the dynamic model. This limits the use of empirical models that cannot quantify the physiological effects.
• Variations in the model parameters from one fermentation to another are to be expected, even when the same control police is applied.
Thus, the control variables affect the system via the kinetic parameters. Calling p(u,t) the function of the kinetic parameters with respect to the control variables u, then the batch reactor dynamics can be described through:
| | (17) |
Usually only a crude empirical function π(u) which is an approximation of the real p(u,t) is known. If an accurate knowledge of the parameter values is required, then an estimation algorithm can be used, expressing p(u,t) as follows:
| | (18) |
where ∆ π(u,t) is an unknown deviation between p(u,t) and π(u). To identify this deviation, the control variable must vary along the whole range of variation. In contrast, when the control variable is kept in a narrow interval during the whole fermentation time, then is not possible to identify ∆ π(u,t). In this case, p(u,t) can be written as follows:
| | (19) |
The sum of π (u) and the estimated value of ∆p(t) provides a better representation of p(u,t) than π(u).
3. A batch kinetic model
A common practice in batch fermentations models is to use the logistic equation for the biomass kinetics together with the Luedeking-Piret equation for the product and main substrate kinetics [Weiss and Ollis (1980)]:
|
| (20.a) |
| | (20.b) |
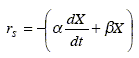 | (20.c) |
Consider the development of a state-space model that uses this set of kinetic equations. As explained in section (2.1), the biomass growth, the product formation and the main substrate oxidation describe an aerobic fermentation with production of a single metabolite. For the first two processes, Eqs. (20.a) and (20.b) can be used as dynamic models. Equation (20.c) corresponds to the total main substrate consumption (the sum of the substrate consumption in each of the three independent processes). Thus, a model for the main substrate oxidation may be obtained by subtracting Eqs. (20.a) and (20.b) divided by their respective stoichiometric yields YX/S and YP/S from Eq. (20.c). Alternatively, it can be assumed that this process is first order in the biomass concentration:
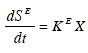 | (21) |
When empirical equations that express the kinetic parameters ( µ, XS, a, b and KE in this case) as functions of the control variables are available, these equations together with Eqs. (20.a), (20.b) and (21) constitute the dynamic model f(x, π(u)). But as explained in section 2.3, it is convenient to add a deviation term or'disturbance-parameter' to each parameter. These disturbances include the errors of the functions π (u). Thus, the process dynamics can be expressed as:
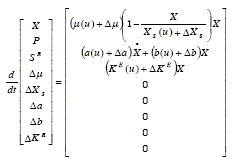 | (22) |
The uncertainty in the 'disturbance-parameters' dynamics suggests to model them as constants with a real-time state and parameter estimator estimating their values.
4. Application to the batch production of xanthan gum. Results and discussion.
Xanthan gum is an extracellular polysaccharide produced by Xanthomonas campestris. This gum has numerous applications and is produced in large quantities. The kinetic model of Eqs. (20) has been used by Weiss and Ollis (1980), Pinches and Pallent (1986) and Shu and Yang (1991) to describe the production of xanthan gum in batch fermentors. Since these authors do not provide a complete information on the main component dynamics, the model of section 2 is used to complete the fermentation description. Pons et al. (1989) developed a structured model for this fermentation and estimated the stoichiometric relations for the gum production, the catabolism of the main substrate (glucose), and the oxidative phosphorilation. The chemical formula of a "mol" of xanthan gum proposed by Pons et al. (1989) is C32.34H48.58O27.36Na1.38. The stoichiometry of xanthan gum production provides the values YP/S = 0.917 g P/g S, YP/CO2 = 34.326 g P/g CO2 and YP/O2 = 15.820 g P/g O2. Also, YS/O2 = 0.937 g S/g O2 and YS/CO2 = 0.682 g P/g CO2 are derived from the stoichiometry of the glucose oxidation. The stoichiometry of biomass production was not reported but can be estimated from some regularities of aerobic fermentations, element balances and the knowledge of the broth composition [Erikson et al. (1978)]. Then, the yields YX/S, YX/O2 and YX/CO2 can be calculated from the experimental value of YX/N.
The cellular maintenance coefficient of Eq. (21) is estimated using Eq. (14). By modelling rP and rS through Luedeking-Piret type equations, then KE results:
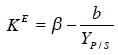 | (23) |
Kinetic expressions for rO2 and rCO2 can be calculated replacing Eqs. (20.a), (20.b), and (21) into Eqs. (7) and (8). Since rP is modeled by the Luedeking-Piret equation, then the 'calculated rates' rO2 and rCO2 will also have the same structure.
In Table 2, the resulting values of some kinetic parameters are compared with experimental values by Pinches and Pallent (1986); Pons et al. (1989); and Peters et al. (1992). As the rates rO2 and rCO2 depend on the biomass concentration, the evolution of this concentration must be simulated for driving these rates. The fermentation conditions of the cited papers and the kinetic equations used for simulating the evolution of the biomass concentration are also summarized in Table 2. Computer simulations are presented in Figs. 2 to 5. In these figures the evolution of the biomass concentration was simulated; the model-predicted evolution of the oxygen consumption (computed as explained in the previous paragraph) is compared with their simulated evolution using the experimental kinetic parameters (Eq. (15) with experimental parameters of Table 2). The predicted carbon dioxide
Table 2: Experimental and calculated values of yields and kinetic parameters for four xanthan gum fermentations carried out in batch reactors (The reported experimental values are given in normal font. The calculated values are given in Italics, and below the experimental values.)
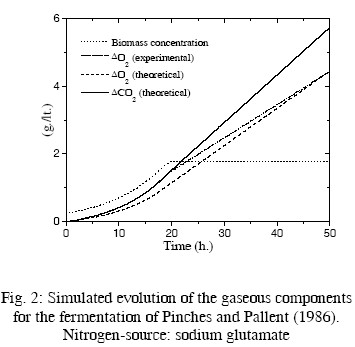
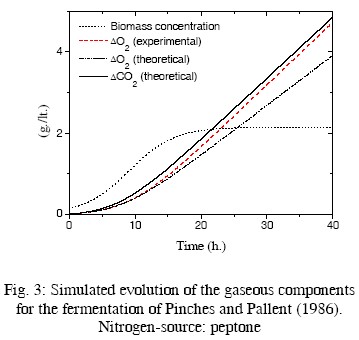
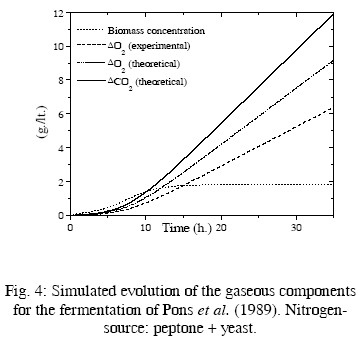
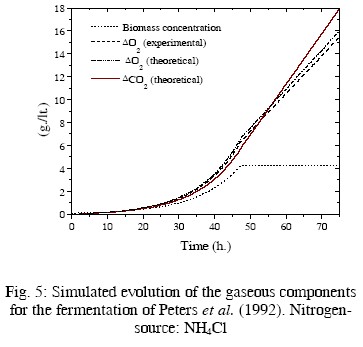
production is also presented. Unfortunately, there is not experimental information on the evolution of this main component. For the fermentation presented in Pinches and Pallent (1986) with sodium glutamate as nitrogen source, the experimental and theoretical evolution of consumed oxygen are quite similar. Interestingly, the theoretical value of c is smaller than the experimental value, while the opposite occurs with the parameter d, indicating a compensation of values. This can be attributed to errors in the graphical method used by Pinches and Pallent (1986) to identify the experimental parameters. For the fermentation of Peters et al. (1992), the agreement For the fermentations of Pinches and Pallent (1986) with peptone as nitrogen source and Pons et al. (1989), the results are not too good. Nevertheless, the differences can be explained by the possible generation of by-products from a complex nitrogen source. Some experimental information by Flores Candia (1994) supports this statement.
In summary, the agreement between the calculated and experimental parameters is acceptable, considering the large uncertainties in this process and the poor measurements of some of the key variables. The use of'disturbance-parameters' seems appropriate in this case.
5. Conclusions
A procedure was outlined for building dynamical models by combining macro and microscopic balances with available kinetic information. A model of the microbial metabolism that is based on elemental and intracellular component balances was presented. The model divides the metabolism into five partial metabolisms or pseudo-reactions. The balances allow to calculate how errors in the kinetics parameters or in the stoichiometry of a partial metabolism influence the remaining process, and also allow to calculate some of the unknown rates. This is useful in a batch process where the biomass grows in a changing environment that can generate strong kinetic disturbances. Kinetic information on fermentations is generally scarce, particularly in the case of the gaseous components interchanged between the broth and the gas phase (O2 and CO2). A procedure was proposed to derive interrelationships between these measured variables and the state variables.
As it was seen in section 2.1, in batch fermentations the main substrate oxidation rate can show considerable variations. Contrary to what is usually assumed, it was shown here that this rate is not first order in the biomass concentration.
Some modern control strategies require of dynamical models. In batch fermentations the kinetic rates are generally unreliable, and for this reason the concept of disturbance-parameters estimated via an estimation algorithm were introduced to improve the quality of the kinetic information.
The proposed procedure was applied to xanthan gum batch fermentations, and the gum production was modeled trough the Luedeking-Piret equation. The equation parameters and some stoichiometric coefficients were used to predict the oxygen consumption and the carbon dioxide production rates. A fairly good agreement with experimental data was observed.
Acknowledgments
We would like to thank Gregorio Meira for helpful and detailed comments on a draft of this paper. This work was supported by the Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET) and the Universidad Nacional del Litoral (UNL).
Nomenclature
| µ | specific biomass growth on the logistic equation (h-1) |
| α | growth associated to the specific main substrate consumptio (g substrate/g biomass). |
| β | steady specific main substrate consumption (g substrate/g biomass h ) |
| γ | growth associated to the specific carbon dioxide production (g CO2 /g biomass) |
| δ | steady specific carbon dioxide production (g CO2 /g biomass h) |
| ∆p | vector of disturbance-parameters |
| ∆CO2 | cumulative carbon dioxide production |
| ∆S | cumulative main substrate consumption |
| ∆SN | cumulative nitrogen source consumption |
| ∆O2 | cumulative oxygen consumption |
| ΦI | net flow rate of component I into the reactor (g I/L h) |
| a | growth associated specific metabolite production (g metabolite/g biomass) adenosine 5-triphosphate (energy carriers) |
| ATP | steady specific metabolite production (g metabolite/g biomass h ) |
| b | growth associated specific oxygen |
| c | consumption (g O2 /g biomass) |
| C | vector of main components concentration |
| d | steady specific oxygen consumption (g O2 /g biomass h) |
| EP | stoichiometry of the metabolite production stoichiometry of the oxidative |
| EPO | phosphorylation |
| ESE | stoichiometry of the main substrate catabolism |
| EX | stoichiometry of the biomass production vector of dynamic functions for the states |
| f(•) | vector of state -measurements relations |
| g(•) | macroscopic specific coefficient of maintenance (g main substrate/g biomass.h) |
| KE | reduced equivalents (electron carriers) |
| NADH2 | concentration of metabolic product (g metabolite/L) |
| P | vector of model parameters |
| p | level of oxidative phosphorylation (ratio |
| P/O | between ATP formed and oxygen consumed on EPO ) |
| rATPM | ATP consumption for maintenance (moles ATP/g biomass h) |
| rC | vector of conversion rates for the main components production rate of carbon dioxide (g CO2/L h) |
| rCO2 | consumption rate of the nitrogen source (g |
| rN | nitrogen source/L.h) consumption rate of oxygen (g O2/L h) |
| rO2 | production rate of metabolite (g |
| rP | Metabolite/L h) oxidative phosphorylation rate (moles |
| rPO | ATP/L.h) consumption rate of main substrate (g main |
| rS | substrate/L h) production rate of biomass (g biomass/L h) |
| rX | main substrate concentration (g main |
| S | substrate/L) concentration of nitrogen source (g Nitrogen |
| SN | source/L) vector of control variables |
| u | biomass concentration (g biomass/L) |
| X | vector of state variables |
| x | stationary biomass concentration (g biomass/L) |
| XS | vector of measurements |
| Y | stoichiometric yield of component I on |
| YI/J | component J (g I/g J) |
References:
1. Agrawal P., Koshy G. and Ramseier M. "An Algorithm for Operating a Fed-Batch Fermentor at Optimum Specific Growth Rate," Biotechnol. Bioeng. Vol. 33, 115-125 (1989).
2. Andrews G. "Estimating Cell and Product Yields," Biotechnol. Bioeng. Vol 33, 256-265 (1989).
3. Andrews G. "The Yield Equations in the Modeling and Control of Bioprocesses," Biotechnol. Bioeng. Vol 42, 549-556 (1993).
4. Asenjo J., W. Sun and J. Spencer. "Optimal Control of Batch Processes Involving Simultaneous Enzimatic and Microbial Reactions," Bioproc. Eng. 323-329 (1995)
5. Constantinides A., J. Spencer and E. Gaden. "II Optimun Temperature Profiles for Batch Penicilin Fermentation," Biotechnol. Bioeng. Vol 12, 1081- 1098 (1970).
6. Diener A. Goldschmidt B. "Suboptimal Control of Fed- Batch Bioprocesses Using Phase Properties" Journal of Biotechnology. Vol. 33, 71-85 (1994)
7. Erikson L., I. Minkevich and V. Eroshin. "Application of Mass and Energy Balance Regularities in Fermentation," Biotechnol. Bioeng. Vol 20, 1595- 1521 (1978).
8. Flores Candia J. "Metabolic Flux Distribution, Modelling and Process Optimization of Xanthan Production," Ph.D. Thesis. Technical University of Braunschweig, Germany (1997).
9. Harmon J., Lyberatos G. and Svoronos S. "A New Method for Adaptive Determination of Optimun pH and Temperature," Biotechnol. Bioeng. Vol. 33, 1419-1424 (1989).
10. Heijnen J.J. and J.A. Roels. "A Macroscopic Model Describing Yield and Maintence Relationships in Aerobic Fermentation Processes," Biotechnol. Bioeng. Vol 23, 739-763 (1981).
11. Lee J., I. Lee and Y. Park. "Optimal pH Control of Batch Processes for Production of Curdlan by Agrobacterium Species," Journal of Ind. Microbiol. and Biotech. 23, 143-148 (1999).
12. Lim H., J. Tayeb, J. Modak and P. Bonte. "Computational Algorithms for Optimal Feed Rates for a Class of Fed-batch Fermentation: Numerical Results for Penicillin and Cell Mass Production," Biotechnol. Bioeng. Vol. 28, 1408-1420 (1986).
13. Minkevich I.G. "Mass-Energy Balance for Microbial Sysntesis – Biochemical and Cultural Aspects," Biotech. Bioeng. Vol 25, 1267-1293 (1983).
14. Modak J. and Lim H. "Feedback Optimization of Fedbatch Fermentation," Biotechnol. Bioeng. Vol. 30, 528-540 (1987).
15. Peters H., Suh I., Schumpe A. and W. Deckwer. "Modeling of Batchwise Xanthan Production," Can. J. Chem. Eng. Vol 70, 742-750 (1992).
16. Pinches A. and L. Pallent. "Rate and Yield Relationships in the Production of Xanthan Gum by Batch Fermentations Using Complex and Chemically Defined Growth Media," Biotechnol. Bioeng. Vol 28, 1484-1496 (1986).
17. Pons A., C. Dussap and J. Bros. "Modelling Xanthomonas Campestris Batch Fermentation in a Bubble Column," Biotechnol. Bioeng. Vol 33, 394- 405 (1989).
18. Reuss M. Computer Control of Bioreactors. "Present Limits and Challenges for the Future. Chemical Process Control," 641-687. Elsevier Austin. (1986)
19. Roels J.A. "Application of Macroscopic Principles to Microbial Metabolism" Biotechnol. Bioeng. Vol 22, 2457-2514 (1980).
20. Roels J.A. "Energetics and Kinetics in Biotechnology," Elsevier (1983).
21. San K. and Stephanopoulos G. "The Effect of Growth Rate Delays in Substrate Inhibited Kinetics on the Optimal Profile of Fed-Batch Reactors," Biotechnol. Bioeng. Vol. 28, 356-361 (1986)
22. San K. and Stephanopoulos G. "Optimization of a Fedbatch Penicillin Fermentation. A Case of Singular Optimal Control with State Constraints," Biotechnol. Bioeng. Vol. 34, 72-78 (1989).
23. Shi Z., Shimizu K., Watanabe N. and Kobayashi T. "Adaptive On-Line Optimizing Control of Bioreactor Systems," Biotechnol. Bioeng. Vol.33, 999-1009 (1989).
24. Shimizu H., Takamatsu T, Shioya S. and K.I. Suga. "An Algorithmic Approach to Constructing the On-Line Estimation System for the Specific Growth Rate," Biotechnol. Bioeng. Vol.33, 354-364 (1989).
25. Shimizu K. "An Overview of the Control System Design of Bioreactors," Advances in Biochemical Engineering. Vol 50, 65-84 (1993).
26. Shioya S. "Optimization and Control in Fed-Batch Bioreactors," Advances in Biochemical Engineering. Vol. 46, 112-142 (1992).
27. Shu Ch. and Yang Sh. "Effects of Temperature on Cell Growth and Xanthan Production in Batch Cultures of Xanthomonas Campestris," Biotechnol. Bioeng. Vol. 35, 454-468 (1991).
28. Takamatsu T., Shioya S, Okada Y. and Kanda M. "Profile Control scheme in Baker's Yeast Fed-batch Culture," Biotechnol. Bioeng. Vol. 27, 1675-1686 (1985).
29. Weiss R. and D. Ollis. "Extracellular Microbial Polisaccharides. I Substrate , Biomass and Product Kinetic Equations for Batch Xanthan Gum Fermentation," Biotechnol. Bioeng. Vol 22, 859- 873 (1980).
30. Williams D., Yousefpour P. and E. Wellington. "Online Adaptive Control of a Fed-batch Fermentation of Sacharomyces Cerevisiae," Biotechnol. Bioeng. Vol. 28, 631-645 (1986).
31. Wu W. T., Chen K.Ch. and Chiou H.W. "On-line Optimal Control for Fed-Batch Culture of Baker's Yeast Production," Biotechnol. Bioeng. Vol. 27, 756-760 (1985). [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ]
Received: January 15, 2001.
Accepted for publication: November 21, 2001.
Recommended by Subject Editor R. Sánchez Peña.