Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.32 n.3 Bahía Blanca jul./sept. 2002
Rheological effects in roll coating of paints
F. Varela López and M. Rosen
Grupo de Medios Porosos, Facultad de Ingeniería, Universidad de Buenos Aires, Argentina
Paseo Colón 850 - C1063ACV Buenos Aires, Argentina.
fvarela@fi.uba.ar - mrosen@fi.uba.ar
Abstract — the aim of this work is the study of the problems that arise during roll coating application of paints on steel sheets. We put in evidence the particular effects due to the non-Newtonian properties of these fluids. At speeds above a certain critical value, the flow of paint through the applicator suffers a hydrodynamical instability called ribbing, which generates a patterned interface on the film applied. Threshold of instability as well as waveform of the pattern is function of rheological properties of paints as well as surface tension. Thixotropy of paints as well as shear-thinning behaviour has been determined for several industrial paints used in the steel industry, and correlated with levelling performance after application.
Keywords — coating, paint, rheology, ribbing
I. INTRODUCTION
Roll coating application is one of the most widely used technique for coating steel sheets, both in continuous or batch processes (Dussing and Michalika (1989), Samways (1989)). Since curing time must be as short as possible, and the coated sheet must overcome conformational processes after curing, the film applied must be thin (about 20 mm) compared to the one obtained by other coating techniques such as curtain or blade coating. Roll coating admits application of thin layers of paint at speeds high enough to satisfy industrial requirements.
However, this process presents operability limits given by hydrodynamical instabilities: above certain threshold, the film applied is no longer uniform, due to the presence of a cellular pattern at the surface (Pitts and Greiller (1961), Benkreira et al. (1981), Savage (1984), Rabaud and Hakim (1989)). This generates a stripped film in the direction of coating, called ‘ribbing', which may or may not be flattened by surface tension before curing, depending on rheological and interfacial properties of paints used. Industrial requirements usually make necessary to operate above this threshold, and for that reason this phenomenon is not an occasional accident but an undesired part of the process.
Among many different roll configurations, we will focus our attention on the two-roll forward roll coater (Fig. 1). Pick-up roll is made of steel and it is partially submerged in a pan filled with paint. As it moves it feeds with paint the nip between this and applicator roll. The amount of paint raised by pick-up roll is a function of roller speed, immersion depth and rheological and interfacial properties of paint. This process is well described by Benjamin et al. (1995). After paint is lifted, is forced to pass through the nip between rollers, where an important shear stress is applied, and then paint flow is splitted into two films, one on the pick-up roll, the other covering the applicator roll's surface. This latter will be the one transferred to the steel sheet, forming a reverse meniscus during application.
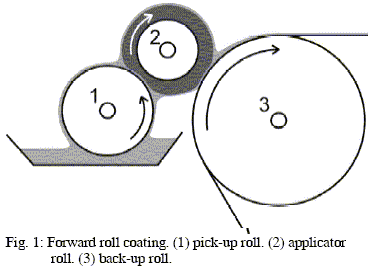
Rheological properties of liquids play an important role in this process. Greener and Middleman (1975), introduces the effect of non-Newtonian viscosity and viscoelasticity on the base flow, showing the changes on pressure gradients and on coated film thickness. Sinha and Singh (1982) also studied the base flow for this geometry. Experimental results obtained for ribbing instability showed that viscoelasticity is a destabilising effect (Bauman et al. (1982), Fernando and Glass (1988), Dontula et al. (1996), Varela López et al. (1999, 2000)). Also changes on pattern waveform are reported (Grillet et al. (1999), Pauchard et al. (1999)). These particular features put in evidence that a correct characterisation of rheological properties of paints used in industrial con text is necessary to understand its performance in this process. In the next sections we will describe some rheological properties of paints as well as the influence of these on the process of roll coating application.
II. RHEOLOGY OF PAINTS
A. Shear-dependent viscosity
Paint flow through the applicator consists of several regions of relatively low shear rates and others of extremely high shear rates. In the case of having a Newtonian fluid, a linear relationship between shear stress and shear rate is satisfied (Acheson 1990):
| | (1) |
Where tij is the stress tensor, m is the viscosity and dij is the deformation rate tensor, defined as
 | (2) |
For such a fluid, the relation between stress and rate of deformation will be the same, regardless of the intensity of the stress applied.
However, paints are known to be non-Newtonian fluids, i.e., that the relation between stress and deformation velocity is non linear
 | (3) |
![]() is the shear rate. For the case of paints, our viscosity measurements are well fitted by Carreau model over a wide range of shear rates (Byrd et. al. 1987):
is the shear rate. For the case of paints, our viscosity measurements are well fitted by Carreau model over a wide range of shear rates (Byrd et. al. 1987):
| | (4) |
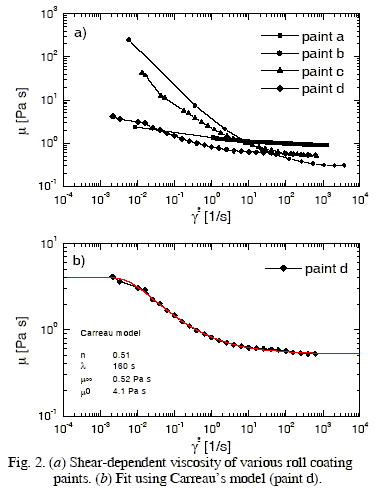
Where m¥ and m0 are the high and low shear rate viscosities respectively, l a characteristic time scale and n and exponent that describes the power-law region at intermediate shear rates. Figure 2a show the shear-dependent viscosity of several paints used in the steel industry. Figure 2b shows the fit obtained for one sample (paint d) with Carreau model. Exponent n is always less that unity in the case of paints. For that reason, viscosity is reduced by shear, and is said to be shear thinning. This behaviour is shared by most polymeric systems, regardless of its elastic properties. Relatively inelastic polymer solutions show strong shear thinning effects even al low concentrations (Zyrnsak et al. 1999).
B. Thixotropy
Paints are suspensions of solids on a polymeric network, forming structures that are highly affected by shear. When a shear stress is applied, the structure is rapidly affected and viscosity is significantly reduced. After cessation of shear, the structure is rebuild, but this process occurs in a time scale that depends on the structural properties of the system. If the application process is fast compared to this ‘rebuilding time', a memory effect on viscosity will be observable, and it will be no longer a local property but a function of the history of deformation.
Thixotropic effects have been observed in the paints we studied (Fig. 3). Transient viscosity has been measured using a cone-plate rheometer, making closed loops between two shear rates, and varying the period of measurement. The memory of deformation is put in evidence comparing the viscosities obtained on the upper and the lower part of the loop. Recovery times are significant in these systems, and thixotropic effects are noticed in the post-application process, during levelling and curing. Rather than being a problem, thixotropy allows having a low viscosity even after cessation of shear, improving levelling and overall coating quality.

From the theoretical viewpoint, thixotropy can be treated as an order-disorder phase transition induced by shear. There exist different approaches in order to analyse thixotropy: from continuum mechanics, from polymer dynamics, and a thermodynamical approach, among others. A good review can be found in Huang (1988). Huang model is well suited for the study of thixotropy in paints and inks (Huang et al. 1976). It predicts a contribution to entropy change due to molecular rearrangement:
| | (5) |
bij is a molecular rearrangement parameter, which is function of deformation rate, T the temperature, r the density and SR the contribution to entropy due to molecular rearrangement. Considering the total entropy change, and assuming a power-law dependence of bij with deformation rate, an expression for viscosity can be derived:
| | (6) |
k is related to the Equilibrium State and C to the structural breakdown rate of the system. When the recovery time occurs rapidly, the expression is simplified to a shear-dependent viscosity constant in time.
III. RIBBING INSTABILITY
Paint flow at the exit of the nip presents a free surface whose position and shape are function of bulk forces and capillary effects (Fig. 4). At speeds below a certain threshold, the meniscus is uniform in the y-direction (except near the edges of the rollers) and paint transfer produces a smooth film over the steel sheet. This critical condition on speed is dependent of rheological and interfacial properties of liquids, and can be stated in non-dimensional form via capillary number Ca, the ratio between bulk (viscous) forces and interfacial effects due to surface tension:
| | (7) |
V is roller speed, m the viscosity and s surface tension. Ca is the control parameter of this instability.

If Ca high enough, the uniform solution loses stability and a pattern appear with a definite wavelength. Amplitude a satisfies a single mode Guinzburg-Landau equation (Rabaud et al. (1990), Bellon et al. (1998), Drazin and Reid (1984)):
| | (8) |
e is the reduced critical parameter, and A is the asymptotic value of amplitude of the pattern. Figure 6 shows the evolution of A with Ca, above and below threshold Ca*. The transition is supercritical.
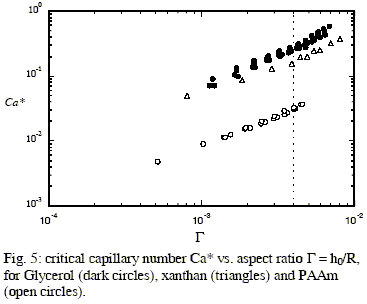
Fig. 6: Pictures of the interface below and above threshold (increasing Ca from up to down). On each picture, air is on the upper side. Minimum gap h0 is exactly located at the lower boundary of each frame. (a) Glycerol (Ca = 0.210, 0.226, 0.262, 0.425); (b) Xanthan 1000ppm (Ca = 0.076, 0.123, 0.155, 0.338); (c) PAAm 1000ppm (Ca = 0.110, 0.124, 0.154, 0.165).
The stability criterion in the case of Newtonian fluids follows from the linear analysis of the growth rate of sinusoidal perturbations. A complete treatment of this problem can be found in Savage (1984) and in Michalland (1992). In a qualitative point of view, a more simple stability criterion is the one postulated by Pitts and Greiller (1961):
| | (9) |
h0 is minimum gap and R is roll radius.
While most of the features of this instability are present in the non-Newtonian case, a series of significant differences has been observed in the case of polymeric liquids, as a function of its elasticity. Figure 5 shows the instability threshold for different polymeric liquids: xanthan in glycerol solvent, and polyacrilamide (PAAm). This one present strong viscoelastic effects at concentrations studied (0.1%). In both cases, however, the (time-independent) viscosity measured as a function of shear rate present qualitatively the same behaviour and is comparable to most commercial paints. For that reason, the results obtained for these polymeric solutions are directly related to the paint response in this process.
As can be observed, the presence of elastic effects on the fluid generates a strong reduction of critical Ca with respect to the Newtonian case, while inelastic xanthan solutions doesn't change threshold significantly. This permit concludes that elastic effects are responsible for this drop on critical conditions. A more general discussion can be found in Varela López et al (2000).
Shape of the pattern above threshold also presents a dependence on rheological properties of fluids. In Fig. 6 we also show the evolution of pattern for three different systems: a Newtonian fluid (Glycerol), xanthan (0.1%) and PAAm (0.1%). The first frame represents meniscus position at threshold, and can be noticed the difference between the elastic solution (c) and the others. This put in evidence that film thickness will be strongly affected by elasticity. Just above threshold, in all cases a sinusoidal pattern appears, according to the Guinzburg-Landau prediction. However, the pattern evolves differently towards peaked fingers (xanthan) and saw-toothed fingers (PAAm)
IV. LEVELING
As it has been stated, under normal operational conditions, the surface of the film is not uniform but stripped. A few seconds after paint is applied, it enters to the oven where curing process begin. For that reason, levelling is expected to occur under this time scale. Following Patton (1964), an estimate of levelling time for a stripped pattern can be derived:
| | (10) |
Where L is the wavelength of the stripped pattern and d the mean film thickness. tl measures the time necessary for a stripped pattern of given amplitude to flatten to a 10% of its original value. Note that not only geometrical film parameters are involved in this expression, but also physical properties of paint play an important role. Paints with relatively low surface tension and high viscosity will be harder to level than other which its viscosity is lower and its interfacial properties are more important.
While interfacial properties are more or less constant during application, viscosity is very dependent on shear rate in most industrial liquid coatings. Paint formulation makes good use of this property in order to improve quality. Viscosity of paints at low shear rate must be high enough to prevent pigment suspension to settle during storage before application (usually a period of several months), and a lower viscosity at high shear rates, during application, to reduce ribbing amplitude.
On the other hand, during levelling, it is desirable to have a low viscosity, in order to have a smoother film before curing. The stresses generated by surface tension during levelling are of the order of 1-10 Pa. The viscosity measured in paints at this level of stress is relatively high with respect to the values reached at the nip between rollers. Replacing in Eq. 1 the value of viscosity estimated for this process, levelling time is significantly overestimated. We think that the origin of this is that the time scales involved in this process are much shorter (< 20 s) than the time paint needs to regain the structure lost during application. This thixotropic effect on paints is very important, with characteristic recovery times of several minutes. For that reason, the viscosity of a paint during levelling is lower than the value obtained in quasi-stationary conditions, even if the stress acting are not very significant. For that reason, special care must be taken for the correct determination of viscosity in this process.
Another important aspect of levelling of paint films is solvent evaporation. If the fluid is evaporating, as in our case, solvent concentration is varying with time as paint dries. But since the pattern is not uniform, this process generates concentration gradients between negative and positive curvature zones. As a consequence, a surface tension gradient appears acting on the surface modifying levelling dynamics (Wilson 1993). These effects have been observed in paints under brushing application, and are reported by Wilson in the same paper. However, since curing is faster in roll coating is expected that solvent evaporation effects in levelling may be masked out by viscosity rise due to polymer entanglement.
V. CONCLUSIONS
In this work we put in evidence that roll coating application is a process where rheological and interfacial properties of paints play an important role on operability conditions. Threshold of ribbing instability dynamics are function of viscosity, and surface tension acts as a stabilising factor for instability and is the driving force for levelling.
High coating speed makes the presence of ribbing unavoidable in many cases, and getting a product of good finishing or not depends on the levelling properties of each coating. For that reason, to have a low viscosity, high surface tension liquid favours levelling. Rheology, via shear-thinning viscosity and thixotropy, combined to an efficient shear process, must generate the optimal conditions for levelling. In order to make this possible, a detailed knowledge of paint properties is necessary, added to a complete description of the flow along the process.
AKNOWLEDGEMENTS
The authors wishes to thank M. Rabaud and C. Allain for fruitful discussions on rheological aspects of ribbing instability, and to Jorge Albertelli (SIDERAR S.A.) for important remarks concerning industrial steel coating. This work has been partially financed by SIDERAR S.A. and is in the frame of ECOS n° A97E03 and PICS (CNRS-CONICET) n°561. F.V.L. has a grant from ‘Academia Nacional de Ciencias Exactas, Físicas y Naturales' of Argentina.
NOTATION
| a = | amplitude of pattern. |
| A = | equilibrium value of amplitude of pattern. |
| C = | thixotropic structural breakdown rate. |
| Ca = | capillary number. |
| Ca* = | critical capillary number. |
| dij = | ij-component of deformation velocity tensor. |
| h0 = | minimum gap between rollers. |
| k = | equilibrium structural parameter. |
| n = | rheological index |
| R = | roller radius |
| SR = | entropy contribution of rearrangement. |
| T = | temperature. |
| tl = | levelling time. |
| ui = | i-component of velocity field. |
| V = | tangential roller speed |
| xi = | coordinate on the i-direction. |
Greek letters:
| bij = | molecular rearrangement parameter. |
| d = | mean film thickness. |
| e = | reduced parameter control. |
| shear rate. | |
| G = | aspect ratio |
| l = | characteristic time scale. |
| L = | wave length of pattern |
| m = | viscosity |
| m0 = | zero-shear viscosity |
| m¥ = | infinite-shear viscosity |
| r = | density |
| s = | surface tension |
| tij = | ij-component of stress tensor. |
REFERENCES
1. Acheson, D. J., "Elementary Fluid Dynamics", Oxford (1990).
2. Bauman T., T. Sullivan and S. Middleman, "Ribbing Instability in Coating Flows: Effect of Polymer Additives", Chem. Eng. Commun. 14, 35-46 (1982).
3. Bellon, L. L. Fourtune, V. Ter Minassian and M. Rabaud, "Wave-Number Selection and Parity-Breaking Bifurcation in Directional Viscous Fingering", Phys. Rev. E 58, 565-574 (1998).
4. Benjamin, D. F., T. J. Anderson and L. E. Scriven, "Multiple Roll Systems: steady state operation", AIChE J. 41, 1045-1060 (1995).
5. Benkreira, H., M. F. Edwards and W. L. Wilkinson, "A semi-empirical model of the forward roll coating flow of Newtonian fluids", Chem. Eng. Sci., 36, 423-427 (1981).
6. Byrd, R. B., Armstrong, R. C., Hassager, O., "Dynamics of Polymeric Liquids" Vol. 1, p.171, Wiley (1987).
7. Dontula P., M. Pasquali, C. W. Macosko and L. E. Scriven, "Viscoelastic effects in forward-roll coating". Proc. XIIth Int. Congr. on Rheology, Aït-Kadi A., Dealy, J.M., James, D.F., Williams, M.C., Editors (1996).
8. Drazin, P. G. and W. H. Reid, "Hydrodynamic stability", p.272, Cambridge University Press (1982).
9. Dussing, H. and F. Michalicka, "Colour coating emphasises clean air and water", Steel Times, December (1989).
10. Fernando, R. H. and J. E. Glass, "Dynamic Uniaxial Extensional Viscosity (DUEV). Effects in Roll Application II. Polymer Blend Studies", J. Rheol. 32, 199-213 (1982).
11. Greener Y., S. Middleman, "A theory of roll coating of viscous and viscoelastic fluids". Polymer Eng. Sci. 15, 1-10 (1975).
12. Grillet, A.M., A. G. Lee, and E. S. G. Shaqfeh, "The stability of elastic fluid interfaces in coating flows", J. Fluid Mech. 399, 49-83 (1999).
13. Huang, C. R. "Characterisation of thixotropic fluids", Encyclopaedia of Fluid Mechanics, vol. 7, N. Cheremisinoff, Ed., Gulf Publishing Co. (1988).
14. Huang, C. R., W. Fabisiak and N. L. Polston, "Correlation of thixotropic parameters with application properties of latex paints", presented at the 7th International congress on rheology, Gothenburg, Sweden (1976).
15. Michalland, S. "Etude des differents régimes dynamiques de l'instabilité de l'imprimeur", Thèse Université Paris VI (1992).
16. Patton, T. C. "Paint Flow and Pigment Dispersion", J. Wiley and Son (1964).
17. Pauchard, L. F. Varela López, M. Rosen, C. Allain, P. Perrot and M. Rabaud, "On the Effects of Non-Newtonian Fluids Above the Ribbing Instability", Proceedings of the 3rd European Coating Symposium, Erlangen, F. Durst, Ed. (1999).
18. Pitts, E. and J. Greiller, "The flow of thin liquid films between rollers", J. Fluid Mech. 11, 33-50 (1961)
19. Rabaud, M. and V. Hakim, "Shape of stationary and travelling cells in the printer's instability", Proceedings of the 3rd International Workshop on instabilities and non-equilibrium structures, Valparaíso, Chile, E. Tirapegui, W. Zeller, Eds., Kluwer Academic Publishers (1989).
20. Rabaud, M., S. Michalland et Y. Couder, "Dynamical Regimes of Directional Viscous Fingering: Spatio temporal Chaos and Waves Propagation", Phys. Rev. Lett. 64, 184 (1990).
21. Samways, N. L., "Armco's 86-in. hot strip mill and coating facilities at the Middletown works", Iron and Steel Eng., April (1989).
22. Savage, M. D, "Mathematical model for the onset of ribbing", AIChE J. 30, 999-1002 (1984).
23. Sinha, P. and C. Singh, "Lubrication of a cylinder on a plane with a non-Newtonian fluid considering cavitation", Trans. ASME, 104, 168-172 (1982).
24. Varela López, F., L. Pauchard, M. Rosen, and M. Rabaud, "Non-Newtonian effects on Ribbing Instability Threshold", submitted to J. Non-Newtonian Fluid Mech. (2000).
25. Varela López, F., L. Pauchard, M. Rosen, and M. Rabaud, "Threshold of Ribbing Instability with Non-Newtonian Fluids", Proceedings of the 3rd European Coating Symposium, Erlangen, F. Durst, Ed. (1999).
26. Wilson, S. K., "The levelling of paint films", IMA J. App. Math. 50, 149-166 (1993).
27. Zyrnsak, M. A., D. V. Boger and V. Tirtaatmadja, "Steady shear and dynamic rheological properties of xanthan gum solutions in viscous solvents", J. Rheol. 43, 627-650 (1999). [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ]
Received: June 15, 2001.
Accepted for publication: December 15, 2001.
Recommended by Subject Editor E. Dvorkin.














