Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Latin American applied research
Print version ISSN 0327-0793
Lat. Am. appl. res. vol.32 no.3 Bahía Blanca July/Sept. 2002
On the modelling of liquid steel processes
M B. Goldschmit*, S. P. Ferro, R. J.Príncipe and A. H. Coppola Owen
Center for Industrial Research, FUDETEC, Córdoba 320, 1054 Buenos Aires, Argentina
*sidgld@siderca.com
Abstract — An iterative (k-L)-predictor / (e )- corrector algorithm that models turbulent flow was developed in previous publications. In this paper, the 3D finite element turbulent model was used to analyze the liquid steel movement produced by gravity force, inert gas stirring or electromagnetic force stirring.
Keywords — turbulence model, continuous casting process, k-e turbulent model, industrial fluid dynamic applications.
I. INTRODUCTION
During the steel manufacturing liquid steel goes through a set of vessels. These vessels are:
- Ladle: where the addition of alloys takes place.
- Tundish: where the liquid steel is distributed among the different lines, and the inclusions are removed by flotation.
- Nozzles: which connect different vessels (ladletundish; tundish-mold).
- Mold: where the steel solidifies taking the final shape.
In these vessels it is important to keep the liquid steel in continuous movement to avoid the cooling and solidification in non convenient places.
The liquid steel can be moved by three different mechanisms in the steelmaking process:
- The gravity force: tundish, submerged entry nozzle, mold.
- The injection of an inert gas: ladle, mold.
- The electromagnetic forces: ladle, tundish, mold.
In this paper we show an example of a numerical model of each mechanism used to move the liquid steel
II. TURBULENCE MODEL
Considering viscous incompressible flow, isothermal flow, constant density (r), constant laminar viscosity (m), buoyancy force (Fb) external forces (Fe) and a turbulence k-e model (k: is the turbulent kinetic energy, e is the turbulent kinetic energy dissipation rate), the following equations are solved:
| | (1) |
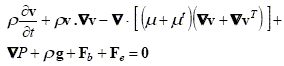 | (2) |
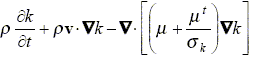 | (3) |
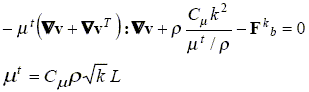 | (4) |
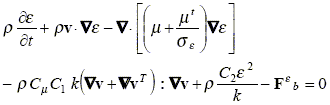 | (5) |
 | (6) |
where v is the time averaged velocity; P is the time averaged pressure; mt is the turbulent viscosity; g is the gravity force; Fk b is the correction of k-transport equation by the buoyancy forces; Fe b is the correction of e-transport equation by the buoyancy forces; L is the mixing length; and the typical constants of k-e model of Launder and Spalding (1974) are Cm = 0.09 , C1 = 1.44 , C2 = 1.92 , sk = 1.0 and se = 1.0.
To solve these equations we use:
- A standard isoparametric finite element discretization for v , k and e.
- Penalization of pressure (Zienkiewicz and Taylor, 2000).
- A Streamline Upwind Petrov Ga lerkin technique (Brooks and Hughes, 1982).
- Trapezoidal rule for time dependent problems (Zienkiewicz and Taylor, 2000).
- A k-L predictor / (e) corrector iterative algorithm (Goldschmit and Cavaliere, 1995, 1997).
- Wall functions as boundary conditions (Príncipe and Goldschmit, 1999).
III. MOVEMENT BY GRAVITATORY FORCE
The movement of liquid steel along the continuous caster is driven by gravity. The quality of the steel and the productivity of the caster depend strongly on the characteristics of the flow of steel through the different vessels of the caster (tundish, submerged entry nozzle, mold). In particular, it is important to know the behavior of the free surface of the liquid steel in these vessels.
A. Pseudoconcentration method
When solving flow problems with a free surface, the location of the interface is also an unknown to be determined as part of the solution. In this work, the pseudoconcentration technique is used to model the flow of a fluid with a free surface. This method solves equations (1)-(6) without buoyancy and external forces (Fb = Fe = Fk b = Fe b = 0) inside an extended domain. This domain includes the volume occupied by the liquid and an extra volume which is filled with a "pseudofluid". The free surface of the fluid is supposed to stay inside this fixed domain along the whole numerical simu lation. To track the free surface, a new variable, C, is introduced. This variable (called pseudoconcentration) satisfies the following equation,
| | (7) |
which is solved using isoparametric finite elements with Streamline Upwind Petrov Galerkin technique (Zienkiewicz and Taylor, 2000).
An arbitrary value of the pseudoconcentration Cc is defined as follows:
- C(x,t) > Cc if x is in the filled region
- C(x,t) < Cc if x is in the empty region
- C(x,t) = Cc if x is in the free surface
The initial value of C, is set according to the initial position of the free surface. Then, the value of C for each time is determined by equation (7) and the position of the free surface is given by those x such that C(x,t) = Cc.
Equations (1)-(6) are solved using the real material properties (viscosity, density, etc..) of the fluid in the filled region and certain artificial properties (the"properties of the pseudofluid") in the empty region. Pseudofluid properties are generally taken low enough, not to affect the dynamics of the real fluid.
It is important to note that the method of pseudoconcentrations prescribes the position of the free surface by the equation C(x,t) = Cc. Then, any position of the free surface may be represented by different pseudoconentration distributions.
In order to prevent numerical errors due to the presence of strong gradients of pseudoconcentration inside the domain, the pseudoconcentration C(x,t) must be a smooth function of position. A smooth initial condition is imposed on the whole domain. To keep the smoothness of C(x,t) , the distribution of pseudoconcentration is re-calculated in each time step (after updating the position of the free surface) with the following equation,
![]()
Where d is the distance to the free surface and s is an arbitrary constant (s = 0.015 in our simulations).
B. Mold problem
As an example of fluid flow driven by gravity with free surfaces, the flow inside a mold is considered. Figure 1 shows a 2D scheme of a slab caster mold with a submerged entry nozzle (SEN).

In order to compare results with experimental measurements, the flow inside a water model mold is simulated with the following parameters,
| - Width of the mold, W | 457 mm |
| - Modeled length of the mold | 686 mm |
| - Inmersion depth of the SEN | 150 mm |
| - SEN diameter, D | 19.5 mm |
| - SEN angle | 20 ° |
| - Speed at SEN entrance, Uo | 780/1340 mm/seg |
Uniform vertical velocity is applied at the SEN entrance as boundary condition. The values of the turbulent variables are kin = aU02 and ein = kin3/2 / (D/2). For the constant a, the value a = 0.00425 is chosen. This value corresponds to tubes and is usually employed in SENs. Wall functions are used to prescribe boundary conditions for velocity and turbulent variables on the rigid walls of the mold and the SEN. On the symmetry line all variables are kept free, except for the normal component of the velocity which is set to zero.
No boundary conditions are imposed on the upper limit of the domain (which is occupied by the pseudo fluid). In the lower limit of the domain the hydrostatic pressure is applied. This takes into account the fact that the fluid is not falling freely but is partially retained by the solidified steel. Pseudoconcentration needs to be imposed at the SEN entrance and eventually (if the fluid is entering the domain) at the lower and upper limits of the domain.
C. Results
Results of numerical model are compared with experimental measurements of the velocity and position of the free surface presented in literature (Panaras et al., 1998; Anagstopoulos and Bergeles, 1999).
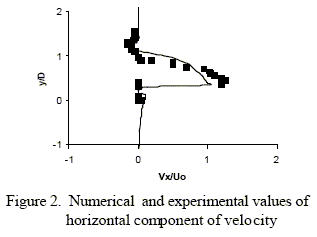
Figure 2 shows the horizontal component of the velocity, Vx, along a vertical line placed at 15 mm from the symmetry line. The figure shows numerical results of the above described method (line) and experimental points (squares). The vertical co-ordinate (y) is measured upwards from the bottom of the SEN. The comparison is repeated in Fig. 3 for the vertical component of the velocity Vy. Both figures correspond to Uo = 780 mm/s.

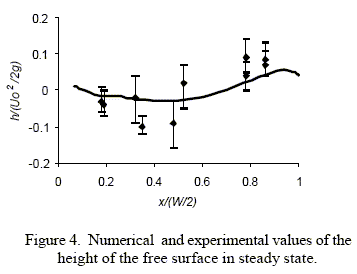
In Fig. 4, the height h of the steady state free surface obtained by numerical computations is compared with experimental results. In this case Uo = 1340 mm/s.
IV. MOVEMENT BY INJECTION OF AN INERT GAS
The stirring of liquid steel contained in a ladle is an example of a flow driven by inert gas injection.
The ladles are near-cylindrical vessels (radius, R » 2 - 3 m; height, H » 2 - 4 m) that contain liquid steel and a surface slag layer (0.1 - 0.4 m) to avoid the reoxidation of steel. In order to obtain a quick chemical and thermal homogenization it is essential to predict where it is convenient to place the gas injection nozzle and to determine the ideal gas flow rate (Qg).
A general scheme of liquid steel movement caused by injection of inert gas in the ladle is shown in Fig. 5.
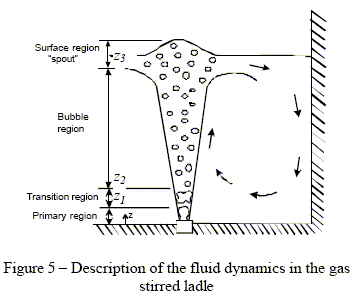
Gas is injected into the liquid steel through a porous nozzle where bubbles are formed; the bubbles rise in the liquid and break up into smaller bubbles and determine two zones:
Two-phase plume zone :
- Primary or momentum region where the flow is governed by inertia forces.
- Transition region where the gas loses its kinetic energy and disintegrates in small bubbles.
- Bubble region where the bubbles rise by the effect of density difference between the gas and liquid steel.
- Surface region, it is the zone closest to the surface.
The primary and transition region in the plume occupy a very small volume of the industrial ladle ( Z2 » 1 to 3 mm; Koria, 1993). Therefore, the buoyancy forces control the fluid dynamics in this zone.
Recirculation zone: it is formed outside the plume zone.
In this work the plume zone is treated as a pseudoone phase (Grevet et al. , 1982; Mazumdar and Guthrie, 1985, 1993) with a lower density
| | (8) |
and the recirculation zone is treated as liquid steel (r = rl); where a is the gas fraction, rg is the gas density and rl is the liquid density. The gas fraction is estimated according to the drift flux model (Mazumdar and Guthrie, 1993) as,
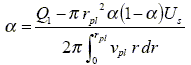 | (9) |
| | (10) |
| | (11) |
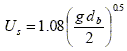 | (12) |

where  ; Tl and Tg are the liquid and gas temperatures [°K]; Patm is the atmospheric pressure [N/m2]; do is the injection orifice diameter [m]; z is the height coordinate of the point; and, Q0 = Q1(z=0).
; Tl and Tg are the liquid and gas temperatures [°K]; Patm is the atmospheric pressure [N/m2]; do is the injection orifice diameter [m]; z is the height coordinate of the point; and, Q0 = Q1(z=0).
In the steady state Navier Stokes equation (2), r g=0 ; Fe = 0 and the buoyancy forces are
| | (15) |
The corrections of the steady state k-transport (3) and e- transport (5) equations Fkb and Feb introduced in our reference Goldschmit and Coppola Owen (in press) to model the buoyancy effect produced by a change of gas fraction in the direction of gravity are
| | (16) |
| | (17) |
A. Validation of the quasi single phase model with a (k-L)-predictor / (e )-corrector turbulent model
In the Table 1 and Fig. 6 we show the result of our numerical model and different water model experiments published in the bibliography

A good agreement is observed between our numerical results and the experimental results.
B. An industrial application
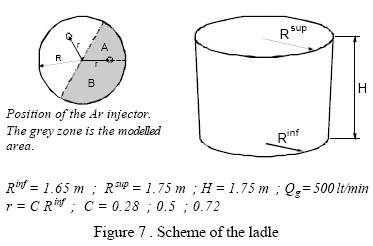
We use our numerical method to find the best positions of the inert gas injector in a ladle. One of these parametric studies analyses the fluid dynamics obtained with two injectors separated by a 120° angle with three radial positions. In Figs. 7 and 8 we show a scheme of the ladle and the velocity distribution in the liquid steel, respectively.
- For the radial injection position r = 0.28 Rinf the liquid steel rises in zone A and goes down in zone B.
- For the radial injection position r = 0.5 Rinf the liquid steel goes down in zone B. In zone A a recirculation is formed in the upper part of the ladle.
- For the radial injection position r = 0.72 Rinf the flow is similar to r = 0.5 Rinf being the recirculation in the zone A deeper.

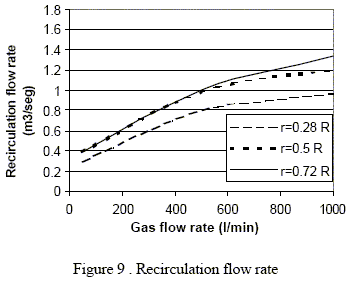
The recirculation flow rate is defined as the total amount of liquid flowing upward or downward through the horizontal mid-plane (Turkoglu and Farouk, 1991). In Fig. 9 we show the recirculation flow as function of the Ar flow rate in each injector of the ladle. The recirculation flow rate increases with the radial position of the injector. The difference between C = 0.28 and C = 0.5 is greater than the difference between C = 0.5 and C = 0.72.
V. MOVEMENT BY ELECTROMAGNETIC FORCES
In this section we describe the stirring of the liquid steel that flows in the continuous casting round mold by the application of an external electromagnetic force. Such a force is obtained by a time dependent electromagnetic field produced by a set of coils connected in pairs. The electromagnetic force can be evaluated as
| | (18) |
where J is the current density and B is the magnetic induction. The current density depends on the steel movement through the constitutive relation
| | (19) |
where v is the steel velocity and s is the electric conductivity. In the second term of the above equation we can see a coupling with the steel motion. However this coupling can be neglected when the magnetic Reynolds number, defined as
| | (20) |
where m is the molecular viscosity and L a characteristic length of the problem, is much smaller than 1 (Moffatt, 1991).
We present results for bar diameter of 0.145 m. In this case the Reynolds magnetic number is 0.03, then the above approximation can be done. The electromagnetic force has been calculated by the CINI' s physics department using a 3D finite element model to solve Maxwell equations (Maldovan et al., 2000; Robiglio et al., 1999). Using this result we solve the k-e model equations (1) to (6) in steady state conditions with Fe as external force and Fb = Fbk = Fbe = g = 0.
The y-Cartesian and the azimuthal electromagnetic force comp onents for a 0.l45 m diameter bar are shown in Fig. 10. It can be seen that this force will produce a rotational movement of the liquid steel.
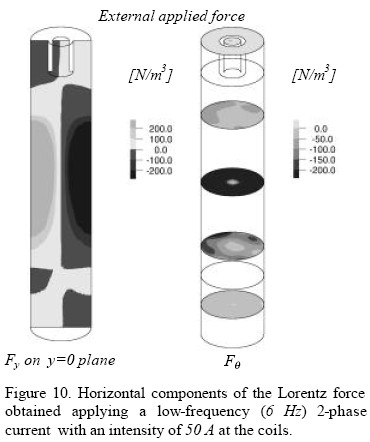
The azimuthal component of the velocity field without electromagnetic stirring and with 6 Hz and 50 A is shown in the Fig. 11. As it can be seen there, there is a rotational movement of the fluid when it is stirred electromagneticaly. Without stirring no azimuthal velocity comp onent is obtained.

In Fig. 12 we present the velocity modulus along a vertical line from the meniscus to the bottom of the computational domain (which is far above the bottom of the mold) with the current intensity as a parameter. This line is located in the external radio, outside the boundary layer. The azimuthal velocity is maximum there, as can be seen in the Fig. 11. In that way we have a measure of the influence of the current intensity on the velocity field.
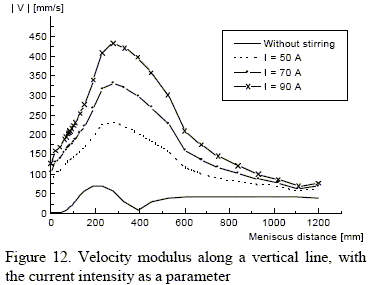
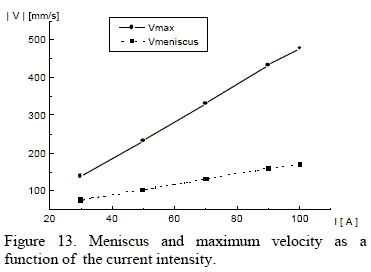
As it is indicated by Shah and More (1982) a minimum value of 250 mm/s for the velocity modulus is needed in order to improve the solidification structure. On the other hand, high velocities in the meniscus area (liquid steel free surface) can cause surface problems on the bar. Some tests carried out in SIDERCA led to an optimal value for the current intensity. With this model we can predict the maximum meniscus velocity, which was found to be around 150 mm/s (Robiglio et al. 1999). In the Fig. 13 we plot the maximum velocity modulus and the meniscus velocity, taken from the line used above. In that way we can evaluate the current intensity we can apply in order to have meniscus velocities lower than this limit. In the example shown in Fig. 13 the maximum acceptable current is about 83 A.
III. CONCLUSIONS
The numerical method allows us to obtain a better understanding of the steel making process.
Numerical results were validated with plant and water model experimental measurements. Then, a good estimation of the fluid dynamics of liquid steel is expected under more general situations where direct measurements are difficult and expensive.
Faced upon these conditions, numerical methods turn out to be a useful tool in the analysis and optimization of liquid steel processes.
ACKNOWLEDGEMENTS
The authors would like to thank Dr. E. N. Dvorkin for his continuous support in numerical methods and Dr. A. Pignotti for giving us the numerical results of the electromagnetic model.
This research was supported by SIDERCA (Campana, Argentina), SIDERAR (San Nicolas, Argentina), SIDOR (Puerto Ordaz, Venezuela), TAMSA (Veracruz, Mexico) and DALMINE (Dalmine, Italy).
REFERENCES
1. Anagbo P.E., and J.K. Brimacombe, "Plume Characteristics and Liquid Circulation in Gas Injection Through a Porous Plug", Metallurgical and Materials Transactions B, 21, 637-648, (1990).
2. Anagstopoulos J. and Bergeles G., "Three-Dimensional Modeling of the Flow and the interface Surface in a Continuous Casting Mold Model", Metallurgical and Material Transactions B, 30B, 1095-1105, (1999)
3. Brooks A.N., and T.J.R. Hughes, "Streamline upwind Petrov-Galerkin formulations for convection dominated flows with particular emphasis on the incompressible Navier-Stokes equation", Comp. Meth. Appl. Mech. Engrg., 32, 199-259, (1982).
4. Goldschmit, M.B., and M.A. Cavaliere, "Modelling of turbulent recirculating flows via an iterative (k-L)- predictor / (e)-corrector scheme", Applied Mechanics Review,48, 11, (1995).
5. Goldschmit, M.B., and M.A. Cavaliere, "An iterative (k-L)-predictor / (e)-corrector algorithm for solving (k-e) turbulent models ", Engineering Computations, 14, 4, 441-455, (1997).
6. Goldschmit M.B., and H. Coppola Owen, "Numerical modeling of gas stirred ladles", Ironmaking and Steelmaking, 28, 4, 337-341, (2001).
7. Grevet J.H., J. Szekely and N. El Kaddah, "An experimental and theoretical study of gas bubble driven circulation systems", Int. J. Heat and Mass Transfer, 25, 487-497, (1982).
8. Johansen S.T. , and F. Boysan, "Fluid dynamics in bubble stirred ladles. Part II: Mathematical modeling", Metallurgical and Materials Transactions B, 19, 755-764, (1988).
9. Koria S.C., "Principles and applications of gas injection in steelmaking practice", Scandinavian Metallurgy, 22, 271-279, (1993).
10. Launder B.E., and D.B. Spalding, "The numerical computation of turbulent flows", Comp. Meth. in Appl. Mech. And Engrg., 3, 269-289, (1974).
11. Maldovan M., J. Príncipe, G. Sánchez, A. Pignotti, and M. Goldschmit, "Numerical modelling of continuous casting of rounds with electromagnetic stirring", European Congress on Computational Methods in Applied Sciences and Engineering, ECCOMAS 2000, Barcelona, España, (2000).
12. Mazumdar D., and R.I.L. Guthrie, "Hydrodinamic modeling of some gas injection procedures in ladles metallurgy operations", Metallurgical and Materials Transactions B, 16, 83-90, (1985).
13. Mazumdar D., and R.I.L. Guthrie, "On mathematical models and numerical solutions of gas stirred ladle systems", Appl. Mathe. Modelling, 17, 255-262, (1993).
14. Moffatt H.K., "Electromagnetic Stirring", Phys. Fluids A 3, 1336-1343, (1991).
15. Panaras G.A., Theodorakakos A., and Bergeles G., "Numerical investigation of the Free Surface in a Continuous Steel Casting Mold Model", Metallurgical and Material Transactions B, 29B,1117-1126, (1998).
16. Príncipe R.J., and M.B. Goldschmit, "Las condiciones de contorno sobre la pared en el modelado de flujo turbulento", Proc. VI Congreso Argentino de Mecánica Computacional, MECOM'99, Mendoza, Argentina, (1999).
17. Robiglio F., A. Campos, J. Paiuk, M. Maldovan, J. Principe, A. Pignotti and M. Goldschmit, "Diseño y modelado numérico del EMS en SIDERCA", 12° Seminario de Acería del IAS y 2° Encuentro de la Sección Argentina de la Iron and Steel Society, Buenos Aires - Argentina, (1999).
18. Shah N.A., and J.J.More, "A review of the effects of electromagnetic stirring (EMS) in continuously cast steel", Iron&Steelmaking, 31-36, October (1982).
19. Turkoglu H., and B. Farouk, "Mixing time and liquid circulation rate in steelmaking ladles with vertical gas injection", ISIJ International, 31, 1371-1380, (1991).
20. Zienkiewicz O.C. , and R.L. Taylor, The Finite Element Method.(5th. Edition), Mc Graw Hill, London (2000). [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ] [ Links ]
Received: July 15, 2001.
Accepted for publication: December 15, 2001.
Recommended by Subject Editor E. Dvorkin.














