Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.33 n.2 Bahía Blanca abr./jun. 2003
Emulsion copolymerization of acrylonitrile and butadiene in an industrial reactor. Mathematical modeling, estimation, and control of polymer quality variables on the basis of calorimetric measurements
J. R. Vega, L. M. Gugliotta and G. R. Meira
INTEC (Universidad Nacional del Litoral - CONICET), 3000 Santa Fe, Argentina lgug@intec.unl.edu.ar
Abstract- An industrial emulsion copolymerization of acrylonitrile and butadiene carried out in a batch (or semibatch) reactor for the production of nitrile rubber (NBR) is investigated. The effect of variable amounts of deactivating impurities on the predictions of a global polymerization model is analyzed; and the advantages of using the model predictions in combination with on-line calorimetric measurements are shown. The adjusted polymerization model allows to adequately monitor main quality variables of the process, such as: monomer conversion, average copolymer composition, average molecular weights, and degree of branching. The semibatch addition of the comonomers and/or the chain transfer agent along the reaction was investigated with the aim of controlling the polymer quality characteristics and increasing the productivity. It is possible to obtain a uniform-composition copolymer with pre-specified profiles of the average molecular weights or the degrees of branching. Furthermore, the NBR productivity can be increased by about 5%, without deteriorating the final copolymer quality with respect to that produced in the more conventional batch operation.
Keywords- Emulsion Copolymerization. NBR. Mathematical Model. Calorimetric Estimations. Polymer Quality Control.
I. INTRODUCTION
The emulsion copolymerization of acrylonitrile (A) and butadiene (B) for the production of NBR is investigated with the aim of estimating the evolution of the main reaction variables and of improving the rubber quality. Such quality is determined by the average values of the copolymer composition, the molecular weights, and the degrees of branching.
Several NBR grades are produced via the "cold" emulsion polymerization process, that mainly differ in their copolymer composition and average molecular weights (Kirk and Othmer, 1981). Batch reactors are generally employed, but semibatch reactors and trains of continuous stirred-tank reactors are also used. Even though NBR has been produced through the emulsion process for more than 50 years, many scientific aspects of its synthesis and characterization still remain unknown.
In general, the polymer quality is improved when the copolymer composition is kept constant along the reaction, and when the levels of branching and cross-linking are maintained below certain values. The degrees of branching and gel contents are normally limited by keeping the monomer conversion below 80%. The most common NBR grade (BJLT), contains a global mass fraction of A of approximately 35%. This value is close to the azeotropic composition (38%), and therefore a small compositional drift is produced under a batch operation. In contrast, other NBR grades with mass fractions of A between 15–34%, exhibit decreasing compositions along the reaction, while increasing composition profiles are observed for global compositions over 38%. The molecular weights are limited by including a chain transfer agent (CTA) or "modifier" in the reaction recipe (Ambler, 1973).
In the standard practice, NBR processes are monitored from on-line reaction temperature measurements in combination with off-line measurements of conversion, copolymer composition, and Mooney viscosity. The presence of varying amounts of impurities like oxygen in the reaction system determines that relatively large batch-to-batch variations are observed. Two global mathematical models for the emulsion copolymerization of A and B have been presented (Dubé et al., 1996; Vega et al., 1997). In Rodríguez et al. (2002) a detailed mathematical model is presented that allows to estimate the molecular weight distributions of each generated branched topology and of the NBR produced along the reaction. Such models are incapable of predicting the real evolution of the NBR process variables in the presence of unknown amounts of reactive impurities. The model predictions can be considerably improved if the conversion is on-line measured or estimated, by using for example gas chromatography, densitometry, Raman spectroscopy or reaction calorimetry.
For the emulsion copolymerization of A and B, the estimation of polymer quality variables (monomer conversion, copolymer composition, molecular weights, and degree of branching) on the basis of energy measurements in combination with a simplified polymerization model has been investigated by Gugliotta et al. (1999). More recently, the control of the molecular structure by addition of monomer or CTA along the reaction has also been considered (Vega et al., 2002).
In this work, three different topics related to the industrial NBR process are considered: 1) the effect of unknown amounts of reactive impurities on quality variables; 2) the advantage of employing on-line calorimetric measurements to predict the evolution of the main process variables, even in the presence of deactivating impurities; and 3) the possibility of increasing the polymer productivity while simultaneously controlling the polymer quality variables along the reaction. To these effects, a previously-developed mathematical model is employed.
II. THE INDUSTRIAL REACTOR AND THE COPOLYMERIZATION MODEL
The industrial reactor (Pecom Energía, S.A., Argentina) is schematically represented in Fig. 1. It consists of a 21000 dm3 stirred tank, where polymerizations are carried out at a controlled temperature of about 10° C. A propane-propylene refrigerant mixture circulates through an internal set of vertical tubes laid out to perform as reactor baffles. The reaction heat is mainly removed by the evaporated refrigerant, that is manipulated in an external control loop to maintain constant the reaction temperature. A second control loop manipulates the refrigerant make-up stream to maintain the liquid refrigerant level in the accumulator. Semibatch additions of A and CTA are used for control purposes. Even though not considered, the addition of any other reagent could be included.
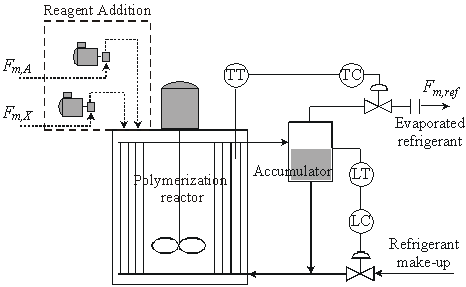
Figure 1. The investigated industrial reactor.
A previously-developed mathematical model (Vega et al., 1997) allows to simulate the semibatch emulsion process. Such model is subdivided into three sections: a) a basic module that calculates the evolution of the gravimetric monomer conversion, xg, the average copolymer composition (or mass fraction of polymerized A in the accumulated polymer), ![]() , the total number of polymer particles, Np, the average number of free radicals per particle,
, the total number of polymer particles, Np, the average number of free radicals per particle, ![]() , the mass fraction of polymer produced in the aqueous phase, and the reagent concentrations in all three phases; b) a particle size module that determines the distribution of particle volumes; and c) a molecular weight module that estimates the number-average and weight-average molecular weights,
, the mass fraction of polymer produced in the aqueous phase, and the reagent concentrations in all three phases; b) a particle size module that determines the distribution of particle volumes; and c) a molecular weight module that estimates the number-average and weight-average molecular weights, ![]() and
and ![]() , and the average number of tri- and tetrafunctional branches per molecule,
, and the average number of tri- and tetrafunctional branches per molecule, ![]() and
and ![]() . The model includes the effect of specific reactive impurities such as oxygen (incorporated with all reagents) and vinyl-acetylene (present in monomer B). In the aqueous phase, oxygen deactivates primary radicals and oxidizes ferrous ions, and in the polymer phase it deactivates polymeric radicals. Those reactions produce the inhibition and/or retardation of the copolymerization reaction, that are observed as a change in the conversion profile (or in the heat rate). The vinyl-acetylene is a "polymerizable" impurity that is incorporated into the polymer molecule inducing branching, thus producing changes in the average molecular weights and branching profiles, but in principle without modifying the conversion evolution. The model was previously adjusted to several batch experiments, and its parameters are reported in Rodríguez et al. (2002) and Vega et al. (2002).
. The model includes the effect of specific reactive impurities such as oxygen (incorporated with all reagents) and vinyl-acetylene (present in monomer B). In the aqueous phase, oxygen deactivates primary radicals and oxidizes ferrous ions, and in the polymer phase it deactivates polymeric radicals. Those reactions produce the inhibition and/or retardation of the copolymerization reaction, that are observed as a change in the conversion profile (or in the heat rate). The vinyl-acetylene is a "polymerizable" impurity that is incorporated into the polymer molecule inducing branching, thus producing changes in the average molecular weights and branching profiles, but in principle without modifying the conversion evolution. The model was previously adjusted to several batch experiments, and its parameters are reported in Rodríguez et al. (2002) and Vega et al. (2002).
In Table 1, two batch industrial recipes (identified as experiments E1 and E2) for producing BJLT grade NBR at 10° C are presented. For the plant operation, the main reagents were first emulsified and cooled to the reaction temperature, and then the initiator was load to start the polymerizations.
Table 1. The Applied Recipes

a diisobutyl hydroperoxide; b intermediate initiator addition (0.075 Kg at t=600 min.); c tert-dodecyl mercaptan.
For the experiment E2, the following variables were on-line measured at a sampling time D t = 2 min: the reaction temperature, Tr; the ambient temperature, Ta; the stirring power, Ws; and the evaporated refrigerant mass flow, Fm,ref . Latex samples were withdrawn along the copolymerizations, and the following variables were off-line measured (see symbols in Fig. 2 and 5): xg, by gravimetry following the ASTM B 1417-80; the (unswollen) number average particle diameter, ![]() , by scanning electron microscopy and UV-vis turbidimetry (Llosent et al., 1996); Np from measurements of xg and
, by scanning electron microscopy and UV-vis turbidimetry (Llosent et al., 1996); Np from measurements of xg and ![]() ;
; ![]() , through the Kjeldahl method; and
, through the Kjeldahl method; and ![]() ,
, ![]() , and
, and ![]() , by size exclusion chromatography with a differential refractrometer and an on-line viscometer. A second indirect estimation of
, by size exclusion chromatography with a differential refractrometer and an on-line viscometer. A second indirect estimation of ![]() (indicated by squares in Fig. 5d) was obtained from
(indicated by squares in Fig. 5d) was obtained from ![]() and
and ![]() , through the following analytical correlation (Small, 1975):
, through the following analytical correlation (Small, 1975): ![]() = 0.5
= 0.5 ![]() /
/![]() - 1.
- 1.
In practice, and for nearly identical recipes and conditions, relatively large batch-to-batch differences in polymerization rates are normally observed. This can be explained by the presence of varying amounts of deactivating impurities (e.g., oxygen) that inevitably contaminate the initial load and inlet flows. To compensate for reduced polymerization rates, intermediate initiator injections are frequently applied.
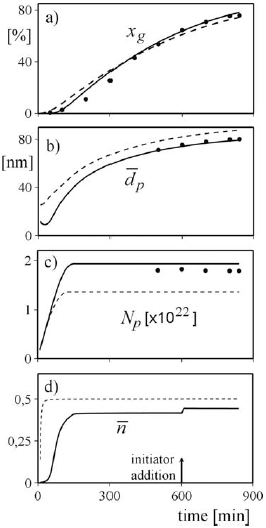
Figure 2. The batch experiment E1. Measured variables (in dots) and model predictions. a) gravimetric conversion; b) number-average particle diameter; c) number of polymer particles; d) average-number of radicals per particle (In dashed lines the O2-free case is represented.)
To illustrate the contribution of oxygen on the model predictions in the experiment E1, Fig. 2 compares model simulation results assuming: i) the absence of oxygen (in dashed lines) and ii) an initial O2 concentration of about 9 ´ 10-4 mol/dm3 (in continuous trace). The presence of oxygen delays the start of the polymerization and distorts the whole conversion profile, but the final conversion results slightly higher than in the O2-free case (Fig. 2a). This may be explained by the fact that the decrease in the polymerization rate due to the reduced ![]() by deactivation (Fig. 2d), is more than compensated by the increase in Np as a consequence of a modified initial nucleation stage (Fig. 2c). The reduction in the polymerization rate per particle is observed in the lower average particle diameters (Fig. 2b). An intermediate initiator addition was applied (to compensate for the presence of O2) after the nucleation period had finished, and for this reason only a step change in
by deactivation (Fig. 2d), is more than compensated by the increase in Np as a consequence of a modified initial nucleation stage (Fig. 2c). The reduction in the polymerization rate per particle is observed in the lower average particle diameters (Fig. 2b). An intermediate initiator addition was applied (to compensate for the presence of O2) after the nucleation period had finished, and for this reason only a step change in ![]() was observed (Fig. 2d).
was observed (Fig. 2d).
From previous results it is observed that, unless the amount of deactivating impurities was adequately measured or estimated, model predictions are normally erroneous. However, with the help of "on-line" calorimetric measurements, the conversion profile estimation could be considerably improved and specific models for calculating Np and ![]() would not be required. Figure 3 shows the evolution of the reaction heat rate, Qr, obtained along two different batch experiments (E2 and E3) with similar initial loads. After the initial nucleation period, that corresponds to a fast growth in Qr, a slight decrease of the heat rate is expected; and this is the behavior observed for experiment E2. However, a more pronounced reduction of Qr, with a minimum at t @ 380 min, is observed for the experiment E3, possibly due to a relatively high level of deactivating impurities. (To increase the polymerization rate in E3, an intermediate initiator addition was applied.). Since deactivating impurities directly reduce the reaction heat rate, then the "on-line" Qr measurements allow to adequately estimate the total monomer conversion.
would not be required. Figure 3 shows the evolution of the reaction heat rate, Qr, obtained along two different batch experiments (E2 and E3) with similar initial loads. After the initial nucleation period, that corresponds to a fast growth in Qr, a slight decrease of the heat rate is expected; and this is the behavior observed for experiment E2. However, a more pronounced reduction of Qr, with a minimum at t @ 380 min, is observed for the experiment E3, possibly due to a relatively high level of deactivating impurities. (To increase the polymerization rate in E3, an intermediate initiator addition was applied.). Since deactivating impurities directly reduce the reaction heat rate, then the "on-line" Qr measurements allow to adequately estimate the total monomer conversion.
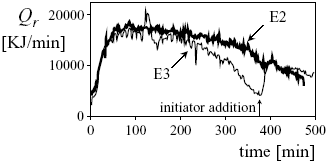
Figure 3. The reaction heat-rate evolutions for two experiments (E2 and E3) with similar initial loads.
The estimation and control of polymer quality variables on the basis of calorimetric measurements will now be considered. To this effect, the general block diagram of Fig. 4a) is proposed. The process computer includes both the estimation and control algorithms. The polymerization system is affected by undesired perturbations (e.g., reactive impurities). From "on-line" non-invasive measured variables (i.e., temperatures and feed rates) combined with a simplified model of the emulsion copolymerization, an open-loop estimator was developed, with the aim of predicting: i) the main polymer quality variables; and ii) some intermediate reaction variables (e.g., monomer and CTA concentrations in the polymer particles, phase volumes, and total moles of free radicals). Then, from such estimated variables, control strategies can be proposed to determine the feed profiles of monomers and/or CTA, that are required to produce pre-specified profiles of the polymer quality variables. In what follows, a more detailed description of the proposed estimation and control policies will be presented.
III. ON-LINE ESTIMATION OF POLYMER QUALITY VARIABLES
Consider now the block diagram of Fig. 4b), that corresponds to a detailed version of the open-loop estimator block of Fig. 4a). For the copolymerization monitoring on the basis of calorimetric measured variables, first the reaction heat rate must be estimated. In the case of a semibatch operation, Qr can be calculated through the following discrete energy balance:
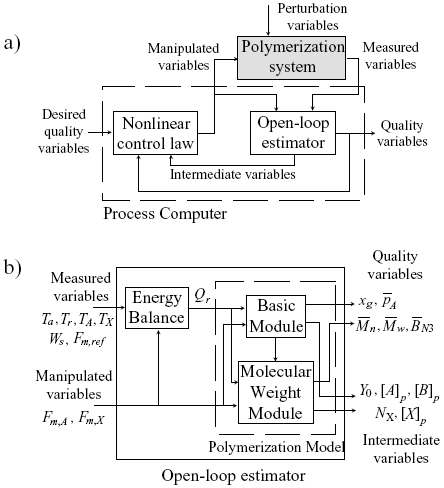
Figure 4. a) General scheme proposed for the estimation and control of polymer quality variables. b) Block diagram proposed for the open-loop estimation on the basis of calorimetric measurements.
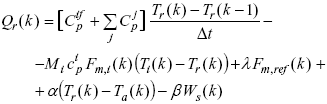 | (1) |
where the first term on the r.h.s. of Eqn. (1) represents the heat accumulated in the internal fittings (e.g., baffles and stirrer) and in the reaction mass; the second term is the heat flow due to the reagent addition (A or X); the third term is the heat flow removed by the refrigerant; the fourth term is the heat flow lost into the environment through the reactor insulator; and the last term is the heat flow introduced by the stirring. Also, ![]() is the heat capacity of the internal fittings; Mi,
is the heat capacity of the internal fittings; Mi, ![]() , Fm,i, and Ti are respectively the molecular weight, the specific heat, the mass flow rate, and the temperature of the added reagent i (i = A, X); mj is the mass of component j (j = A, B, X, water, copolymer);
, Fm,i, and Ti are respectively the molecular weight, the specific heat, the mass flow rate, and the temperature of the added reagent i (i = A, X); mj is the mass of component j (j = A, B, X, water, copolymer); ![]() (=
(=![]() ) is the heat capacity of component j; k (=t/D t) is the discrete time; l is the "effective" latent heat of vaporization of the propane-propylene refrigerant; and a , b are previously determined constants.
) is the heat capacity of component j; k (=t/D t) is the discrete time; l is the "effective" latent heat of vaporization of the propane-propylene refrigerant; and a , b are previously determined constants.
From the calculated evolution of Qr, the main reaction variables (polymer quality and intermediate) are estimated by using a simplified polymerization model (which does not require mathematical expressions for calculating Np and ![]() ). Two estimation levels are considered. In the simpler one, the gravimetric conversion and the copolymer composition are calculated from the basic module. To this effect the following parameters are required: enthalpies of homopolymerization of monomers A and B; reactivity ratios of A and B, rA and rB; and monomer partition coefficients. In the more complex level,
). Two estimation levels are considered. In the simpler one, the gravimetric conversion and the copolymer composition are calculated from the basic module. To this effect the following parameters are required: enthalpies of homopolymerization of monomers A and B; reactivity ratios of A and B, rA and rB; and monomer partition coefficients. In the more complex level, ![]() ,
, ![]() , and
, and ![]() are calculated from the molecular weight module, that requires some intermediate variables calculated in the basic module. In this case, the following extra parameters must be known: constants of propagation, transfer to the monomer, transfer to the CTA, transfer to the polymer, and CTA partition coefficients. The numerical algorithm involved in the estimator include a set of nonlinear difference equations, but they are not here presented for space reasons and can be consulted in Gugliotta et al. (1999) and Vega et al. (2002).
are calculated from the molecular weight module, that requires some intermediate variables calculated in the basic module. In this case, the following extra parameters must be known: constants of propagation, transfer to the monomer, transfer to the CTA, transfer to the polymer, and CTA partition coefficients. The numerical algorithm involved in the estimator include a set of nonlinear difference equations, but they are not here presented for space reasons and can be consulted in Gugliotta et al. (1999) and Vega et al. (2002).
The results obtained from the open-loop estimator for the experiment E2 are indicated in Fig. 5. The quality variable estimations are presented in Fig. 5a-d); while the estimation of some intermediate variables, like the volume of monomer phase, Vm, the total moles of free radicals, Y0, the monomer concentrations in the polymer particles, [A]p and [B]p, and the CTA concentration in the polymer particles, [X]p, are represented in Fig. 5e,f).
In Fig. 5a), an almost direct proportionality between Qr and Fm,ref is observed; thus indicating that the third term of Eqn. (1) is considerably larger than any of the others. In Fig. 5b), the conversion and copolymer composition estimates are compared with the corresponding "off-line" measurements, and a good agreement is observed. The initial comonomers ratio is somewhat below the azeotropic composition, an for this reason a decreasing ![]() profile is observed. In Fig. 5c,d), the estimates of average molecular weights and trifunctional branching are compared with the experimental values. The variation of
profile is observed. In Fig. 5c,d), the estimates of average molecular weights and trifunctional branching are compared with the experimental values. The variation of ![]() is moderate and this is a consequence of an almost constant ratio between the rate of propagation and the rate of chain transfer to the CTA. The branching reactions increase with conversion; and this explains the increasing profiles of
is moderate and this is a consequence of an almost constant ratio between the rate of propagation and the rate of chain transfer to the CTA. The branching reactions increase with conversion; and this explains the increasing profiles of ![]() , and
, and ![]() .
.
From Fig. 5e,f), it is noted that: i) the oscillations in Y0 are a result of the noise in Qr; ii) the second interval of the emulsion polymerization finishes at t @ 270 min., when the monomer phase volume falls to zero; iii) the concentration of comonomers in the polymer phase are relatively constant while the monomer phase is still present, and thereafter they both decrease; and iv) the concentration of CTA in the polymer phase decreases monotonically along the reaction.

Figure 5. The batch experiment E2. a) Measured refrigerant mass flow, and estimated reaction heat rate; b) gravimetric conversion and copolymer composition; c) average molecular weights; d) average degree of branching; e) monomer phase volume and total moles of radicals; and f) monomer and CTA concentrations in the polymer particles. (Quality measured variables are indicated by symbols).
IV. SIMULATED CLOSED-LOOP CONTROL OF POLYMER QUALITY AND INCREASE OF PRODUCTIVITY
Reconsider now the block diagram of Fig. 4a) with the aim of controlling the polymer quality variables. The semibatch addition of A is adopted to control ![]() , and the manipulation of X is considered to independently control
, and the manipulation of X is considered to independently control ![]() or
or ![]() . The control of
. The control of ![]() will not be considered because it remains practically self-controlled under the batch operation (see Fig. 5c). To simulate the polymerization system, the global mathematical model by Vega et al. (1997) was used. The required feed profiles were calculated by numerical inversion of the simplified polymerization model, where Y0 is directly estimated from Qr.
will not be considered because it remains practically self-controlled under the batch operation (see Fig. 5c). To simulate the polymerization system, the global mathematical model by Vega et al. (1997) was used. The required feed profiles were calculated by numerical inversion of the simplified polymerization model, where Y0 is directly estimated from Qr.
In what follows, the problems of controlling copolymer composition, weight-average molecular weight, and branching degree are considered.

Figure 6. The proposed strategies for controlling: a) the copolymer composition through a model-based policy, and b) the average degree of branching through a P+D algorithm.
A. Model-Based Control of Copolymer Composition
Figure 6a) shows the calculation scheme for the control of the copolymer composition. The strategy aims at producing a copolymer with a constant and pre-specified mass fraction of A, ![]() = 0.35. From the basic module of the simplified polymerization model, a (discrete) nonlinear control law that calculates the required mass flow profile of A, Fm,A, was derived:
= 0.35. From the basic module of the simplified polymerization model, a (discrete) nonlinear control law that calculates the required mass flow profile of A, Fm,A, was derived:
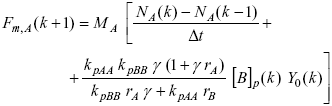 | (2) |
where MA is the molecular weight of monomer A; NA are the moles of unreacted A; kpAA, kpBB are the homopropagation rate constants for A, B; and g (=[A]p0/[B]p0) is the ratio of the comonomer concentration in the polymer particles at the beginning of the reaction, which can be calculated from ![]() (Gugliotta et al., 1995). For its numerical implementation, Eqn. (2) requires the three following estimated states: NA, [B]p, and Y0, calculated by the open-loop estimator. The initial load of A required to obtain
(Gugliotta et al., 1995). For its numerical implementation, Eqn. (2) requires the three following estimated states: NA, [B]p, and Y0, calculated by the open-loop estimator. The initial load of A required to obtain ![]() at the reaction start resulted NA0=1681 Kg, and it was calculated employing the expressions presented in Vega et al. (2002). All other initial loads coincided with those employed in the experiment E2. In Fig. 7a), the required Fm,A, calculated through the proposed algorithm is presented. Fig. 7b) shows that according to the simulations it is indeed possible to obtain a copolymer of uniform composition. For comparison, the batch evolutions corresponding to the experiment E2 are also included. Even though not shown, under copolymer composition control the final NBR exhibits lower values of polydispersity and degree of branching with respect to the batch, with negligible effects on the profiles of conversion and number-average molecular weight.
at the reaction start resulted NA0=1681 Kg, and it was calculated employing the expressions presented in Vega et al. (2002). All other initial loads coincided with those employed in the experiment E2. In Fig. 7a), the required Fm,A, calculated through the proposed algorithm is presented. Fig. 7b) shows that according to the simulations it is indeed possible to obtain a copolymer of uniform composition. For comparison, the batch evolutions corresponding to the experiment E2 are also included. Even though not shown, under copolymer composition control the final NBR exhibits lower values of polydispersity and degree of branching with respect to the batch, with negligible effects on the profiles of conversion and number-average molecular weight.
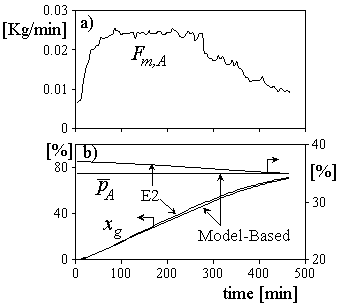
Figure 7. The simulated copolymer composition control. a) Required mass flow of A; b) conversion and copolymer composition. (The simulated batch experiment E2 is also shown.)
B. Model-Based Control of the Weight Average Molecular Weight
This control strategy aims at producing a polymer with a uniform ![]() =
= ![]() = 200000 g/mol. From the simplified polymerization model, a (discrete) nonlinear control law that calculates the required mass flow profile of X, Fm,X, was derived (its calculation scheme is not presented for the sake of space):
= 200000 g/mol. From the simplified polymerization model, a (discrete) nonlinear control law that calculates the required mass flow profile of X, Fm,X, was derived (its calculation scheme is not presented for the sake of space):
 | (3) |
where MX is the molecular weight of the CTA, NX represents the moles of CTA, kp is the pseudo-rate constant of propagation, CX is the ratio between the pseudo-rate constant of transfer to the CTA and kp; and ![]() is the required concentration of CTA in the polymer particles to produce the desired molecular weight. Except for the initial charge of CTA (NX0 = 22.8 Kg), that was calculated employing a similar procedure to that presented in Gugliotta et al. (2001), all other initial conditions coincided with the batch experiment E2. The required CTA profile, Fm,X, is shown in Fig. 8a). It rapidly increases after depletion of the monomer droplets at t @ 270 min. Fig. 8b) indicates that it is indeed possible to produce the required flat profile of
is the required concentration of CTA in the polymer particles to produce the desired molecular weight. Except for the initial charge of CTA (NX0 = 22.8 Kg), that was calculated employing a similar procedure to that presented in Gugliotta et al. (2001), all other initial conditions coincided with the batch experiment E2. The required CTA profile, Fm,X, is shown in Fig. 8a). It rapidly increases after depletion of the monomer droplets at t @ 270 min. Fig. 8b) indicates that it is indeed possible to produce the required flat profile of ![]() . For comparison, the batch evolutions corresponding to the experiment E2 are also included. The evolutions of xg and
. For comparison, the batch evolutions corresponding to the experiment E2 are also included. The evolutions of xg and ![]() almost coincide with the corresponding batch evolutions, and for this reason they are not reproduced here. The average molecular weights and the average degree of branching are represented in Fig. 8b,c). The final
almost coincide with the corresponding batch evolutions, and for this reason they are not reproduced here. The average molecular weights and the average degree of branching are represented in Fig. 8b,c). The final ![]() is lower than in the batch E2, but the polydispersity is slightly higher.
is lower than in the batch E2, but the polydispersity is slightly higher.

Figure 8. The simulated control of weight-average molecular weight (a-c) and degree of branching (d-f). a), d) Required mass flow of X; b), e) average molecular weights; c), f) average number of tri-functional branches per molecule (The simulated batch experiment E2 is also shown.)
C. Proportional-derivative Control of the Degree of Branching
For the control of ![]() a fixed value of this variable cannot be specified without seriously affecting the other quality variables. Instead, a trajectory with an increasing desired value
a fixed value of this variable cannot be specified without seriously affecting the other quality variables. Instead, a trajectory with an increasing desired value![]() has to be chosen. For the present simulation study, the linear variation presented in Fig. 8f) was selected for
has to be chosen. For the present simulation study, the linear variation presented in Fig. 8f) was selected for ![]() . In this case, a proportional-derivative (P+D) algorithm was selected, because the model-based control law produces important deviations in the presence of measurement noise (Vega et al., 2002). Fig. 6b) shows the adopted calculation scheme for the control of
. In this case, a proportional-derivative (P+D) algorithm was selected, because the model-based control law produces important deviations in the presence of measurement noise (Vega et al., 2002). Fig. 6b) shows the adopted calculation scheme for the control of ![]() . From the simplified polymerization model an estimation of
. From the simplified polymerization model an estimation of ![]() is obtained. This estimated value is compared to the desired one, and on the basis of that difference (or error) the (discrete) P+D controller allows to calculate the required mass flow profile of X, Fm,X. All the initial conditions were adopted identical to the batch E2. The required CTA profile is shown in Fig. 8d); and again the CTA mass flow must be rapidly increased after disappearance of monomer droplets. When compared to the batch E2, the final
is obtained. This estimated value is compared to the desired one, and on the basis of that difference (or error) the (discrete) P+D controller allows to calculate the required mass flow profile of X, Fm,X. All the initial conditions were adopted identical to the batch E2. The required CTA profile is shown in Fig. 8d); and again the CTA mass flow must be rapidly increased after disappearance of monomer droplets. When compared to the batch E2, the final ![]() and average molecular weights adopted lower values.
and average molecular weights adopted lower values.
D. Increase of Conversion without affecting the Quality Variables
Reconsider now the previously-described strategies, but with the aim of also increasing the final conversion without deteriorating the polymer quality obtained in the batch operation. To this effect, higher initiator loads (WI) are employed with respect to the batch E2 (WI,batch). In Table 2, the simulated initiator load ratios, WI / WI,batch, and the final NBR properties obtained under each control strategy are presented. With composition control, it is possible to increase the global conversion by about 3%, and simultaneously improve the rubber quality (constant composition and reduced polydispersity). Even though not shown, the final conversion can be increased by about 5% with respect to the batch by adding A at a constant feed rate. However, this produces a polymer with an increasing ![]() profile (i.e., inverted with respect to the batch case). With
profile (i.e., inverted with respect to the batch case). With ![]() control, the monomer conversion can be increased by about 6%, while
control, the monomer conversion can be increased by about 6%, while ![]() remains unaffected. However, the final rubber exhibits a lower
remains unaffected. However, the final rubber exhibits a lower ![]() and a larger polidispersity with respect to the batch. Similarly, the control of
and a larger polidispersity with respect to the batch. Similarly, the control of ![]() allows to increase the final conversion and simultaneously reduce the degree of branching, but at the cost of lowering the average molecular weights.
allows to increase the final conversion and simultaneously reduce the degree of branching, but at the cost of lowering the average molecular weights.
V. CONCLUSIONS
In the industrial emulsion NBR process the presence of variable amounts of deactivating impurities distorts the conversion and reaction heat rate profiles, thus producing important batch-to-batch variations. In particular, the oxygen affects the number of particles and the average number of radicals per particle, which in turn produce changes in the particle diameter and conversion evolutions.
The use of "on-line" calorimetric measurements enables to drastically reduce batch-to-batch changes, because they allow to accurately estimate the monomer conversion along the reaction. Conversion is a key system variable, in the sense that it determines the evolution of most other polymer quality variables. Thus, good conversion estimates in combination with a representative simplified model ensure reasonable open-loop estimates of the polymer quality, even though in practice they are unobservable from energy measurements.
Table 2. Final NBR properties with increased conversions (Simulation results)

Simulation results show that it is possible to produce: i) a uniform composition copolymer with the conversion increased by approximately 3%, without deteriorating the final polymer quality; ii) a polymer of an almost constant ![]() with the conversion increased by about 6%, but with
with the conversion increased by about 6%, but with ![]() reduced by about 10%; and iii) a polymer with a linear trajectory of
reduced by about 10%; and iii) a polymer with a linear trajectory of ![]() at an increased conversion but with a higher polydispersity.
at an increased conversion but with a higher polydispersity.
Uncertainties in the initial loads and/or in the model parameters lead to erroneous estimates of the polymer quality variables, when open-loop estimators based on calorimetric measurements are used. Polymerizing and branching impurities (e.g., vinyl-acetylene), do practically not change the conversion profile; and for this reason, they can not be detected by calorimetric measurements. However, such impurities seriously affect the weight-average molecular weight and the degree of branching. In practice, when any of previous situations appears, additional "on-line" measurements are required to adequately estimate and control the polymer quality variables.
Notation
A, B = acrylonitrile, butadiene.
![]() ,
, ![]() = average number of tri- and tetra-functional branches per molecule (dimensionless).
= average number of tri- and tetra-functional branches per molecule (dimensionless).
![]() = specific heat of reagent i (i = A, B, X, copolymer, and water) (KJ/Kg C).
= specific heat of reagent i (i = A, B, X, copolymer, and water) (KJ/Kg C).
![]() = heat capacity of the internal fittings (KJ/C).
= heat capacity of the internal fittings (KJ/C).
![]() = heat capacity of reagent i (i = A, B, X, copolymer, and water) (KJ/C).
= heat capacity of reagent i (i = A, B, X, copolymer, and water) (KJ/C).
CX = ratio between the pseudo-rate constant of transfer to the CTA and the pseudo-rate constant of propagation (dimensionless).
![]() = number average particle diameter (nm).
= number average particle diameter (nm).
Fm,i = mass flow of reagent i (i = A, X) (Kg/min.).
Fm,ref = refrigerant mass flow (Kg/min.).
[i]p = concentration of species i (i = A, B, X) in the polymer phase (mol/dm3).
k = (t/D t) = discrete time (dimensionless).
kp = pseudo-rate constant of propagation in the polymer phase (dm3/mol min.).
kpAA, kpBB = homopropagation rate constants in the polymer phase (dm3/mol min.).
MA = 53.06 g/mol = molecular weight of A.
MB = 54.09 g/mol = molecular weight of B.
mi = mass of reagent i (i = A, B, copolymer, water, and initiator) (Kg).
![]() ,
, ![]() = number- and weight-average molecular weights (g/mol).
= number- and weight-average molecular weights (g/mol).
MX = 202.4 g/mol = molecular weight of X.
Ni = moles of reagent i (i = A, B, X) (mol).
Np = total number of polymer particles (dimensionless).
![]() = average number of free radical per particle (dimensionless).
= average number of free radical per particle (dimensionless).
![]() = average mass fraction of polymerized A in the copolymer (dimensionless).
= average mass fraction of polymerized A in the copolymer (dimensionless).
Qr = reaction heat rate (KJ/min.).
rA, rB = reactivity ratios of A and B (dimensionless).
t = time (min.).
Ta = ambient temperature (C).
Ti = inlet temperature of reagent i (i = A, X) (C).
Tr = reaction temperature (C).
Vm, Vp = volumes of monomer phase and polymer phase (dm3).
Ws = stirring power (KJ/min.).
xg = gravimetric conversion (dimensionless).
X = chain transfer agent.
Y0 = total moles of free radicals (moles).
Greek Symbols
a = global heat transfer coefficient for the heat lost into the environment (J/C min.).
b = stirring heat coefficient (dimensionless).
g = constant defined as [A]p0/[B]p0 (dimensionless).
l = "effective" latent heat of vaporization of the refrigerant (a propane-propylene mixture) (J/g).
D t = time interval between two consecutive measurements (min.).
Superscripts
0 = indicates initial load or initial value.
d = indicates desired value (or set point).
Acknowledgments
We are grateful to Pecom Energía S. A. (Argentina) for providing us with the experimental data and samples. We also thank CONICET, SeCTIP, and Universidad Nacional del Litoral for the financial support.
REFERENCES
Ambler, M.R. , "Studies on the Nature of Multiple Glass Transitions in Low Acrylonitrile, Butadiene-Acrylonitrile Rubbers", J. Polym. Sci., Polym. Chem. Ed., 11, 1505 (1973). [ Links ]
Dubé, M.A., A. Penlidis, R.K. Mutha and W.R. Cluett, "Mathematical Modeling of Emulsion Copolymerization of Acrylonitrile/Butadiene", Ind. Eng. Chem. Res., 35, 4434-4448 (1996). [ Links ]
Gugliotta, L.M., J.R. Leiza, M. Arotçarena, P.D. Armitage and J.M. Asua, "Copolymer Composition Control in Unseeded Emulsion Polymerization using Calorimetric Data", Ind. Eng. Chem. Res., 34, 3899 (1995). [ Links ]
Gugliotta, L.M., J.R. Vega, C.E. Antonione and G.R. Meira, "Emulsion Copolymerization of Acrylonitrile and Butadiene in an Industrial Batch Reactor. Estimation of Conversion and Polymer Quality from On-Line Energy Measurements", Polym. React. Eng., 7, 4, 531-552 (1999). [ Links ]
Gugliotta, L.M., A. Salazar, J.R. Vega and G.R. Meira, "Emulsion Polymerization of Styrene. Use of n-nonyl Mercaptan for Molecular Weight Control", Polymer, 42, 2719-2726 (2001). [ Links ]
Kirk, R.E. and D.F. Othmer, Encyclopedia of Chemical Technology. 3rd. Ed., 1, 427-442, New York (1981). [ Links ]
Llosent, M.A., L.M. Gugliotta, and G.R. Meira, "Particle Size Distribution of SBR and NBR Latexes by UV-Vis Turbidimetry Near the Rayleigh Region", Rub. Chem. Tech., 69, 4, 696-712 (1996). [ Links ]
Rodríguez, V.I., D.A. Estenoz, L.M. Gugliotta and G.R. Meira, "Emulsion Copolymerization of Acrylonitrile and Butadiene. Calculation of the Detailed Macromolecular Structure", Int. J. Polym. Mat. (in press) (2002). [ Links ]
Small P., "Long Chain Branching in Polymers", Adv. Polym. Sci., 18, 1- 64 (1975). [ Links ]
Vega, J.R., L.M. Gugliotta, R.O. Bielsa, M.C. Brandolini and G.R. Meira, "Emulsion Copolymerization of Acrylonitrile and Butadiene. Mathematical Model of an Industrial Reactor", Ind. Eng. Chem. Res., 36, 1238-1246 (1997). [ Links ]
Vega, J.R., L.M. Gugliotta, and G.R. Meira, "Emulsion Copolymerization of Acrylonitrile and Butadiene. Semi-Batch Strategies for Controlling Molecular Structure on the Basis of Calorimetric Measurements", Polym. React. Eng., 10, 1&2, 59-82 (2002). [ Links ]
Received: September 16, 2001.
Accepted for publication: August 14, 2002.
Recommended by Guest Editors: J. Cerdá, S. Díaz y A. Bandoni.














