Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.33 n.2 Bahía Blanca abr./jun. 2003
Optimal design of stable processes
A. M. Blanco and J. A. Bandoni
Planta Piloto de Ingeniería Química - PLAPIQUI (UNS-CONICET)
Camino La Carrindanga Km. 7, 8000 Bahía Blanca, ARGENTINA
e-mail: abandoni@plapiqui.edu.ar
Abstract—Open loop dynamic stability is a major feature of operability. An optimization approach for open loop stable process design is presented. It is based on Lyapunovs stability theory and formulated as an eigenvalue optimization problem. The resultant non-linear semi-definite programming problem is reformulated into an interior-point / logarithmic-barrier- transformation programming problem. The proposed methodology is applied to the design of a three states stirred tank reactor.
Keywords—Optimization. Process Design and Stable Design.
I. INTRODUCTION
The interaction between process design and process operability is an active research area. Design for operability is necessary because the sought of steady state economic optimality only, may lead to designs with poor operational features. Several approaches have been proposed to carry out such an interaction. In terms of philosophies it can be mentioned (Lewin, 1999) the use of heuristics, the operability measures approach and the complete integration of design and operability. The first approach is mostly based on experience and is widely applied in conceptual design (Douglas, 1988).
Operability measures describe particular operability features and are applied as screening tools to evaluate alternative designs. Controllability and resiliency measures (Barton et al., 1991), relative gain array, singular value indices, etc., are the most relevant within this category. Finally, integration between design and operability stands for the explicit inclusion of operability elements within the process design formulation. This is clearly the most ambitious approach both from a modeling and resolution point of view. Luyben and Floudas (1994), for example, proposed a multi objective optimization approach between economics and some controllability index. Mohideen et al. (1996) posed and solved a design plus a control system (feedback PI) superstructure. Besides its inherent difficulties, the trend of design is in the sense of integration.
Operability is a wide concept, which involves optimality, dynamics, flexibility in the face of uncertainty, risk, environmental concern, etc. As pointed out by Wolff et al. (1994), open loop stability and optimality are major properties of operability, and should be considered simultaneously at the design stage. Economic optimality is a natural objective in chemical process design. Open loop dynamic stability is an issue of paramount importance, which should be ensured by proper design. It is the purpose of this contribution to present an integrated approach to design / operability, which explicitly considers economic optimality and open loop dynamic stability. Within the framework of Lyapunovs stability analysis, the design formulation with dynamic stability constraint on the steady state operating point is posed as an eigenvalue optimization problem. The proposed approach is first introduced with a simple motivating example and then applied to the meaningful jacketed exothermic stirred tank reactor (CSTR). A considerable effort has been devoted to the study of the dynamics, in particular the stability issue, of the CSTR (Russo and Bequette, 1995). Lyapunovs stability theory has been applied mostly as an analysis tool in such studies. Kokossis and Floudas (1994) presented a systematic methodology applicable to the optimal design of stable process systems focused on complex reaction networks synthesis. They propose an iterative matrix measure relaxation algorithm in order to ensure that the system jacobian matrix is Hurwitz and hence local stability of the resulting design. Within the same philosophy, an alternative approach, based on Lyapunov direct method from a design point of view, is proposed in this work.
II. LYAPUNOV´S STABILITY THEORY
In the present section, most relevant issues of Lyapunov´s Stability Theory are outlined. See, for example, Vidyasagar (1993) for a complete analysis.
For the general non-linear system ![]() , stability of the equilibrium point
, stability of the equilibrium point ![]() has local meaning. For asymptotic local dynamic stability we understand the existence of a certain neighborhood around the equilibrium point within which asymptotically stable trajectories originate. This means that any trajectory starting inside this "domain of attraction" (Fig. 1) approaches the equilibrium point as time increases. We are not interested at the moment in the shape or size of such a region but just on its existence. Consider the free, autonomous system:
has local meaning. For asymptotic local dynamic stability we understand the existence of a certain neighborhood around the equilibrium point within which asymptotically stable trajectories originate. This means that any trajectory starting inside this "domain of attraction" (Fig. 1) approaches the equilibrium point as time increases. We are not interested at the moment in the shape or size of such a region but just on its existence. Consider the free, autonomous system:
![]() ,
, ![]() (1)
(1)
By linearizing around the origin we have, ![]() , where
, where ![]() . Then, it can be proved (Vidyasagar, 1993) that 0 is an exponentially stable local equilibrium of (1) if all eigenvalues of A have negative real parts (if A is a Hurwitz matrix). Moreover, the quadratic form
. Then, it can be proved (Vidyasagar, 1993) that 0 is an exponentially stable local equilibrium of (1) if all eigenvalues of A have negative real parts (if A is a Hurwitz matrix). Moreover, the quadratic form ![]() (which resembles an energy function) is a suitable Lyapunov function for system (1) (which means that A is a Hurwitz matrix) if P is a real, symmetric positive definite matrix and
(which resembles an energy function) is a suitable Lyapunov function for system (1) (which means that A is a Hurwitz matrix) if P is a real, symmetric positive definite matrix and ![]() (energy function derivative with respect to time), verifies that Q is also real, symmetric and positive definite.
(energy function derivative with respect to time), verifies that Q is also real, symmetric and positive definite.
Matrices A, P and Q are related through Lyapunovs matrix equality:
![]() (2)
(2)
Usual practice is to chose matrix Q to be a positive definite symmetric matrix (in general the identity matrix). Then, provided A, Lyapunov equation (2) is solved for P, also symmetric. If P is positive definite then A is a Hurwitz matrix.

Figure 1: Domain of attraction
III. EIGENVALUE OPTIMIZATION
Eigenvalue optimization arises when the elements of a matrix A depend on an amount of variables, say x, and the values of such variables are desired to be the solution of an optimization problem involving the eigenvalues of A(x) as objective functions or constraints. Our particular interest in eigenvalue optimization is related to the contents of the previous section where the connections between eigenvalues and system dynamics (mostly the stability issue) are apparent. It is the purpose of this section to provide a brief overview of the most relevant topics about eigenvalue optimization. For a comprehensive survey on the subject see Lewis and Overton (1996). The main difficulty arising in eigenvalue optimization problems is the potential coalescence of eigenvalues. The eigenvalues of a matrix with differentiable elements (smooth in the optimization variables) are themselves non-differentiable (non-smooth) at the points where coalescence occurs. It is also frequent that the optimization objective tends to make the eigenvalues coalesce at the solutions (Overton, 1992). Then it is necessary to develop specialized optimization methods to overcome this difficulty. An amount of well-developed theory is available for the case of eigenvalue optimization of symmetric matrices depending linearly on the optimization variables and subject to linear inequalities and to Linear Matrix Inequalities (LMIs).
A LMI has the form F(y)>0, where F is a symmetric matrix whose elements depend linearly on y and >0 stands for positive definiteness condition. LMIs theory and applications is an active research field. A classic reference on the subject is Boyd et al. (1994). The general non-linear unsymmetric case has been far less boarded although some meaningful results have been obtained in the field of structural design (Ringertz, 1997). This contribution is an attempt to apply some of those results in the chemical engineering area. Most of the eigenvalue optimization theory has been developed for real, symmetric matrices. It is known that such matrices have real eigenvalues. Unsymmetric matrices, on the other hand, have complex eigenvalues in general. It is possible, however, to translate the constraint on the real part of the eigenvalues of a real unsymmetric matrix (say A) to be negative, into a positive definiteness condition on a real symmetric matrix (P) through Lyapunovs matrix equality (2). Since it is a sufficient and necessary condition for a real symmetric matrix to be positive definite, its eigenvalues to be positive, the condition on the eigenvalues of the "difficult" unsymmetric matrix A is translated into another condition on the eigenvalues of the "not-so-difficult" symmetric matrix P. In order to avoid the potential non-smoothness arising in eigenvalue optimization, interior-point / logarithmic-barrier-transformation techniques have been successfully applied (Ringertz, 1997). For a comprehensive reference of interior-point optimization, see Fiacco and McCormick (1990). Making use of logarithmic and matrix determinant properties, it will be shown that the potentially non-smooth constraints on the eigenvalues of matrix P may be expressed in terms of the determinant of matrix P, which is a smooth function of the optimization variables.
IV. PROBLEM FORMULATION
The basic general problem of (steady state) design may be posed as a constrained, non-linear, optimization-programming problem (NLP). Stability is considered, according to the results of section 2, by constraining the dynamic system jacobian matrix A to be Hurwitz:
 | (3) |
Here, y is the vector of optimization variables. In general, F (y) is an economic type objective function, h(y) is the set of equality constraints (mass and energy steady-state balances, geometric and equilibria relationships, etc.) and g(y) is the set of inequalities (operational and design constraints). l i stands for eigenvalue. Such a problem may be non-smooth because of the eigenvalue constraints (Ringertz, 1997), considering that h(y) and g(y) are themselves smooth. In order to avoid the difficulties of solving problem (3), the stability issue is considered by adding Lyapunovs equation (2) to the steady state model of the system and requiring positive definiteness on symmetric matrix P=[pij] (or equivalently but better posed numerically on P-1). Matrix Q is chosen to be symmetric and positive definite (usually Q = I):
 | (4) |
The above is a non-linear semi-definite programming problem because of the positive definiteness requirement on matrix P-1, that implies that l i(P-1)>0, i=1, .., n, then:
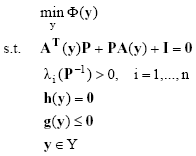 | (5) |
Such problems may be efficiently tackled via interior-point methods. In terms of a logarithmic barrier transformation, problem (5) is reformulated as (Ringertz, 1997):
 | (6) |
since
![]() =
= ![]() = log(det(P-1)) = -log(det(P)), provided that positive definiteness on matrix P is verified. The solution of (6) converges to that of (5) for a decreasing sequence of barrier parameters {m k} as m k ® 0. The above ideas are illustrated through a simple example presented in Kokossis and Floudas (1994).
= log(det(P-1)) = -log(det(P)), provided that positive definiteness on matrix P is verified. The solution of (6) converges to that of (5) for a decreasing sequence of barrier parameters {m k} as m k ® 0. The above ideas are illustrated through a simple example presented in Kokossis and Floudas (1994).
Motivating Example
Consider the optimization problem:
z = min x22
associated with the dynamic system:
![]()
![]()
and variable constraints:
![]()
![]()
![]()
x1 and x2 are the state variables and p is a design parameter. The classic steady state formulation would be:
z = min x22
s.t.
0 = x12 + x22 - 1
0 = x12 + x2 - 4p
![]()
![]()
![]()
whose solution is z* = 0, x1* = -1, x2* = 0 and p* = 0.25. The jacobian matrix of the dynamic system is A = [aij]:
![]()
This matrix is not Hurwitz at the solution, (l 1(A) =-2 and l 2(A) = 1), hence the system is unstable. In order to consider the stability issue, the model is formulated as (6):
![]()
s.t.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
The solution of the above problem is z*=0.258, x1*=-0.861, x2*=0.508 and p* = 0.312. As expected the system is stable since l 1(A) = -0.683 and l 2(A)=-0.040.
V. CHEMICAL ENGINEERING EXAMPLE
From Devia and Luyben (1978), the dynamics of a typical CSTR in which an homogeneous, exothermic, first order, A® B reaction is taking place, is described by the following set of equations (Fig. 2):
 | (7) |
 | (8) |
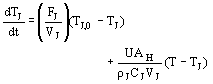 | (9) |
The following constraints also hold because of design and operational reasons:
HR = 2DR (10)
| (11) |
| (12) |
VJ = 0.25 VR (13)
In this model, feed and product streams are at a constant rate. Reactor volume was assumed constant, as well as all physical properties. Metal walls of reactor, jacket and agitator were neglected. Perfect mixing was assumed in the reactor and in the jacket. The reactor is a vertical cylindrical vessel with a height to diameter ratio of two.

Figure 2: Three states CSTR
For simplicity sake, the volume of the cooling jacket is considered to be a fraction (quarter) of the volume of the reactor. In the general case, however, this relation is nonlinear in nature. The following bounds on the variables were considered for optimization purposes, ![]() ,
, ![]() ,
, ![]() and
and ![]() . The Jacobian matrix elements are reported in the appendix. Since heat transfer area is related to the square of the diameter, and reactor volume is related to the cubic of the diameter, certain designs may result unstable if enough heat-transfer capacity per unit volume is not achieved, as reported in Devia and Luyben (1978) for a number of cases. In order to generate stable designs, an economic type objective function is optimized, subject to the (steady state) model of the CSTR (7)-(13) and the Lyapunovs equation (2) for Q = I (which provides six single equations) as required by (6). A total cost objective function to be minimized has been considered:
. The Jacobian matrix elements are reported in the appendix. Since heat transfer area is related to the square of the diameter, and reactor volume is related to the cubic of the diameter, certain designs may result unstable if enough heat-transfer capacity per unit volume is not achieved, as reported in Devia and Luyben (1978) for a number of cases. In order to generate stable designs, an economic type objective function is optimized, subject to the (steady state) model of the CSTR (7)-(13) and the Lyapunovs equation (2) for Q = I (which provides six single equations) as required by (6). A total cost objective function to be minimized has been considered:
Cost = 1917 DR1.066 HR0.802 + 120 FJ
The objective involves capital and operability costs and is intended to represent typical total cost nonlinearities. The parameters are rather arbitrary and have to do with cost of manufacturing the jacketed vessel in the first term and with the cost of the cooling fluid in the second. Productivity is not explicitly considered in the objective function since output reactant concentration is restricted to be low and then high conversion is achieved in the reactor. The design problem was solved for increasing reactor feed flow rates, F, from 50 cu. ft./ h to 150 cu. ft./h, and the numerical data of Table 1. The proposed formulation was implemented in GAMS / MINOS5 modeling language (Brooke et al., 1996) and the optimization results are reported in Table 2. Such designs are open loop stable, since the corresponding jacobian matrices are Hurwitz.
Table 1: System data


VI. ALGORITHMICS
As already commented, the determinant of matrix P being positive is not a sufficient condition for matrix P being positive definite. Along the optimization process it may happen that the determinant becomes zero or negative (undetermining the logarithm and producing a runtime error), or remains positive but not verifying matrix P positive definiteness. In order to cope with such situations, Ringertz (1997) recommends to check matrix P positive definiteness before evaluating the objective function in each iteration. If violation occurs backtracking should be performed in the line-search until feasibility is achieved (consider that feasibility in the starting point is required in interior point techniques). For the general case, an algorithm that checks positive definiteness on P in each iteration (by evaluating its eigenvalues, for example) and the step-length parameter in line-search reduced until positive definiteness condition is achieved may be applied. In this work, the described interior-point / logarithmic-barrier-transformation problem, both for the motivating example and for the CSTR, has been solved with standard NLP solvers and positive definiteness of matrix P checked only at the solution. Such an pproach worked satisfactorily here due to the small size and not very involved dynamics of the systems but it is not expected to perform successfully for larger and more complex models. In such cases, the aforementioned algorithm or alternative formulations should be applied.
VII. CONCLUSIONS
Two major operability properties have been considered in the present contribution: open loop stability and optimality. Stability in a Lyapunov sense is explicitly considered within the design formulation, arising an interior-point / logarithmic-barrier- transformation optimization problem. Such an integrated approach leads to an inherently locally stable design as result of the optimization. Some other outstanding operability features as flexibility, i. e. system ability to cope with uncertainty, and controllability and switchability, properties related to dynamic response quality between operating states, should be also considered within the process design formulation. Future work will cover these topics.
Notation
A: jacobian matrix
A: reactant
AH: heat transfer area
B: product
CA: reactant concentration in reactor liquid
CA,0: reactant concentration in feed stream
CJ: heat capacity of jacket water
Cp: heat capacity of reactor liquid
E: activation energy
f: general deviation function vector
F: feed rate
FJ: jacket cooling water rate
P: Lyapunovs theorem matrix
Q: Lyapunovs theorem matrix
R: perfect gas constant
T: temperature of the reactor
TJ: jacket cooling water temperature
TJ,0: inlet cooling water temperature
T0: feed temperature
t: time
U: overall heat transfer coefficient
V: Lyapunov function
VR: reactor volume
VJ: jacket volume
x: general deviation state vector
a : pre-exponential factor
r : density of reactor liquid
r J: density of cooling water
D HR: heat of reaction
l i: eigenvalue
Appendix: Jacobian matrix elements of CSTR

REFERENCES
Barton, G. W., W. K. Chan and J. D. Perkins, "Interaction Between Process Design and Process Control: The role of Open-loop Indicators", J. Proc. Cont. 1 (may), 161-170 (1991). [ Links ]
Boyd, S., L. E. Ghaoui, E. Feron and V. Balakrishnan, Linear Matrix Inequalities in System and Control Theory, SIAM Philadelphia (1994). [ Links ]
Brooke, A., D. Kendrick and A. Meeraus; GAMS Release 2.25 (1996) [ Links ]
Devia, N. and W. L. Luyben, "Reactors: size versus stability", Hydrocarbon Processing June 1978; 119-122 (1978). [ Links ]
Douglas, M., Conceptual Design of Chemical Processes, McGraw-Hill (1988) [ Links ]
Fiacco, A. V. and G. P. MacCormick, Nonlinear Programming, volume 4 of Classics in Applied Mathematics; SIAM, Philadelphia (1990). [ Links ]
Kokossis, A. C. and C. A. Floudas, "Stability in Optimal Design: Synthesis of complex Reactor Networks", AIChE J. 40, 849-861 (1994). [ Links ]
Lewin, D. R., "Interaction of Design and Control", presented at the 7th IEEE Mediterranean conference on control and automation, Haifa (1999). [ Links ]
Lewis, A. S. and M. L. Overton, "Eigenvalue Optimization", Acta Numerica; Cambridge University Press, 149-190 (1996) [ Links ]
Luyben, M. L. and C. A. Floudas, "Analyzing the Interaction of Design and Control-1. A Multi-objective Framework and Application to Binary Distillation Synthesis", Comp. Chem. Eng. 18, 933-969 (1994). [ Links ]
Mohideen, M. J., J. D. Perkins and E. N. Pistikopoulos, "Optimal Design of Dynamic Systems under Uncertainty", AIChE J. 42, 2251-2272 (1996). [ Links ]
Overton, M., "Large-Scale Optimization of Eigenvalues" SIAM J Optimization 2, 88-120 (1992). [ Links ]
Ringertz, U. T., "Eigenvalues in Optimum Structural Design", in Proceedings of an IMA Workshop on Large-Scale Optimisation (A. R. Conn, L. T. Biegler, T. F. Coleman and F. Santosa, eds.) Part I, 135-149 (1997). [ Links ]
Russo, L. P. and B. W. Bequette, "Impact of Process Design on the Multiplicity Behavior of a Jacketed Exothermic CSTR", AIChE J. 41, 135-147 (1995). [ Links ]
Vidyasagar, M., Non-linear Systems Analysis, Prentice-Hall (1993). [ Links ]
Wolff, E. A., J. D. Perkins and S. Skogestad, ESCAPE 4 Proceedings, 95-102 (1994). [ Links ]
Received: September 16, 2001.
Accepted for publication: August 28, 2002.
Recommended by Guest Editors J. Cerdá and S. Díaz.














