Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.33 n.2 Bahía Blanca abr./jun. 2003
An optimal approach to the multiple-depot heterogeneous vehicle routing problem with time window and capacity constraints
R. Dondo, C. A. Méndez and J. Cerdá
INTEC (UNL - CONICET)
Güemes 3450 - 3000 Santa Fe - ARGENTINA
jcerda@intec.unl.edu.ar
Abstract. The vehicle routing problem (VRP) has become a crucial industrial issue for its impact on product distribution costs. Though quite important in practice, the time-constrained version of the VRP accounting for several types of vehicles and m- depots, called the extended VRP with time windows (m-VRPTW), has received less attention. Since it is an NP-hard problem, most of the current approaches to m-VRPTW are heuristic, thus providing good but not necessarily optimal solutions. This work presents a novel MILP mathematical framework for the m-depot heterogeneous-fleet VRPTW problem. The new optimization approach permits to find both the optimal vehicle route/schedule and the fleet size by choosing the best set of preceding nodes for each pick-up point. To get a significant reduction on the problem size to tackle larger m-VRPTW problems, some elimination rules have been embedded in the MILP framework. When applied to a pair of examples, it was observed a remarkable saving in computer costs with regards to prior VRPTW optimization methods.
Keywords: VRPTW. MILP Formulation. Soft/Hard Time Windows.
I. INTRODUCTION
In recent years, vehicle routing problems (VRP) have received much attention due to the importance of selecting efficient distribution strategies. Surveys on VRP problems can be found in Bodin et al. (1983) and Desrosiers et al. (1995). Vehicle routing problems with time windows (VRPTW) have recently become an area of intensive research since time windows naturally arise from realistic considerations and their impact on the optimal solution must be taken into account. Similarly to VRP, VRPTW problems are NP-hard too. Exact algorithms developed for solving VRPTW are described in Kolen et al. (1987), Desrochers et al. (1992) and Fisher et al. (1997). Though heuristic techniques still remain as the unique tool available for solving very large-scale VRP, optimization methods are becoming more effective to deal with problems of moderate size. Nevertheless, traditional optimizing formulations still require an exceptionally large number of variables and constraints to represent real routing problems. In order to widen the scope for optimizing approaches, this work introduces a new MILP formulation for the m-depot VRPTW problem, also called m-VRPTW, based on a continuous time domain representation and a separate handling of vehicle assignment and node sequencing decisions.
II. PROBLEM FORMULATION
Let the road network be described by {I, P, A} with I = {i1, i2, ..., in} denoting the set of nodes or customers, and P = {p1, p2, ..., pl}representing the set of depots where the vehicles V = {v1, v2, ..., vm} are housed. Nodes and depots are connected through a network of minimum cost arcs A = {dij / i,j Î (I È P)}. Each node represents a client that has a non-negative commodity production pri to be picked up and transported to a depot pÎ P. There is a matrix of unit routing costs C = {cijv} and a matrix of vehicle speeds G = {g ijv} associated to the set A. Each node has its time window [ai, bi], where ai is the earliest arrival time and bi is the latest visiting time. The service time on node i by vehicle v is (tfi + pri / rv), where tfi is the fixed stop time on node i and rv is the loading rate of goods on vehicle v. The solution to the problem must comply the following constraints: (i) each route starts and ends on the same depot; (ii) each node belongs to exactly one route; (iii) the total amount of commodity assigned to vehicle v must never exceed its capacity qv ; (iv) the duration of the trip for any vehicle v should be shorter than the maximum allowed routing time tvvmax; (v) the node i should be serviced within the time window [ai, bi]. The problem goal is to minimize the total cost of providing pickup service to every node. Three types of costs are considered in the objective function: fixed costs for using vehicles, traveling costs along the selected routes and penalty costs fining soft time-window and maximum routing time constraints violations.
III. THE MATHEMATICAL MODEL
Assignment of nodes to vehicles
Each node must belong to exactly one tour.
| | (1) |
Assignment of vehicles to depots
Each vehicle can at most be assigned to a single depot.
| | (2) |
Capacity constraints
The total amount of commodity to be picked up by vehicle v must not exceed its capacity qv.
| | (3) |
Minimum routing cost for visiting node i
The routing cost from the starting depot p to node i by the assigned vehicle v takes a minimum value if one makes the trip all the way through the least cost route dpi connecting depot p to node i.
 | (4) |
Relationship between visiting costs for nodes (i,j)
The routing cost from the starting depot to node j by the assigned vehicle v must never be lower than the cost of visiting node i if both nodes are on the same tour (Yiv = Yjv = 1) and node i is visited earlier (Sij = 1). Otherwise, the reverse statement will be true. A value of MC equal to 1.2-1.3 times the maximum routing time tvvmax multiplied by both the average vehicle speed and the average unit traveling cost is adopted.
| | (5.a) |
 | (5.b) |
Overall routing cost for used vehicle v
The overall traveling cost for the tour assigned to the used vehicle v must never be lower than the cost of visiting any particular node i on the tour plus the cost of returning from i to the starting depot p through the minimum cost route dip.
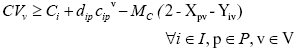 | (6) |
Minimum visiting time for node i
The visiting time for node i by the assigned vehicle v takes a minimum value if one makes the trip all the way through the least cost route dpi connecting depot p to node i.
 | (7) |
Relationship between visiting times for nodes (i,j)
The time at which node j is visited by the assigned vehicle v must never be lower than the visiting time for node i if both nodes are on the same tour (Yiv = Yjv = 1) and node i is visited earlier (Sij = 1). Otherwise, the reverse statement will be true. A value for the parameter MT equal to the maximum routing time tvvmax multiplied by a factor close to 1 (» 1.1 to1.2) is adopted.
| | (8.a) |
 | (8.b) |
Overall routing time for used vehicle v
The overall routing time for the used vehicle v must never be lower than the visiting time for a particular node i on the tour plus both the loading time and the return time from i to the starting depot p through the minimum cost route dip.
 | (9) |
Time constraint violations due to early arrivals
![]() (10)
(10)
Time constraint violation due to late arrivals
![]() (11)
(11)
Routing time constraint violation
![]() (12)
(12)
Objective function
 | (13) |
Assignment constraints (1) and (2) together with routing constraints (4)-(6) define the feasible space for the traditional VRP. Timing constraints are considered through visiting time constraints (7)-(9) and the time constraint violations (10)-(12). No sub-tour breaking constraints are necessary. The major features of the proposed mathematical formulation are: (i) the use of a continuous representation for both the time domain and the routing cost domain; (ii) the separate handling of vehicle assignment and node sequencing decisions through different sets of binary variables; (iii) the definition of 0-1 sequencing variables based on the concept of generalized predecessor. A comparative analysis of computational requirements for solving Example 1 using either the proposed model or the classical slot-based m-VRPTW formulation (Bodin et al., 1983) is made in the next Section.
IV. EXAMPLE 1
Production at 10 nodes must be picked-up and transported to a processing plant P, with a fleet of at most 2 vehicles housed on P. Problem data are summarized in Table 1. Maximum routing time and
time windows are all considered as hard constraints by setting D a, D b and D Tv all equal to zero in eqns. (10) to (12) .
Only traveling costs were included in the objective function. Fixed costs are also considered in Example 2. The best solution for Example 1 is shown in Table 2. Model sizes and computational requirements for this approach and the traditional m-VRPTW formulation (Bodin et al., 1983) are compared in Table 3. It can be noted that the number of binary variables in the proposed MILP approach is reduced by more than three times and, consequently, the required CPU time decreases by a factor of 7.5.
Table 1. Data for Example 1
Table 2. Optimal solution for Example 1
V. ELIMINATION RULES FOR DISCARDING NON-OPTIMAL ROUTES
Though the proposed approach sharply reduces the problem size, VRP type problems are combinatorial. Nevertheless, problem data can be used to cut down the problem size. To this purpose, exact time window-based elimination rules and distance-based heuristic rules are presented.
A. Time window-based elimination rules
- If one vehicle cannot service a pair of nodes without violating time windows constraints, then two different vehicles must be assigned to service such nodes. Mathematically this condition is expressed as follows:  | (14) |
Therefore (Yjv + Yiv £ 1) and the vehicle v can service the node i or the node j but not both. Thus, for any pair of nodes { i,j} satisfying condition (14), constraints (5.a)-(5.b) and (8.a)-(8.b) can be eliminated. Moreover, the sequencing variable Sij is no longer needed.
- Let us suppose that nodes i and j are assigned to the same vehicle v and the sum of the earliest arrival time to node i (ai) plus the travel time between such nodes, including the service time at node i, is higher than the latest arrival time to node j. Then, node i cannot be visited before node j and Sij = 0 if both nodes are on the same tour. Consequently, the sequencing variable Sij can be eliminated from the problem formulation.  | (15) |
Thus, inequalities (5.a) and (8.a) can be dropped from the model while constraints (5.b) and (8.b) reduce themselves to eqns. (16) and (17), respectively.
 | (16) |
| | (17) |
 | (18) |
Thus, constraints (5.b) and (8.b) can be dropped from the model and inequalities (5.a) and (8.a) reduce to:
| | (19) |
| (20) |
B. Distance-based heuristic rules
- Two far away nodes cannot be assigned to the same vehicle because it would lead to very high travelling costs, and possible violations of the routing time constraint. This condition can be stated as follows: ![]() (21)
(21)
where dmax is a model parameter selected by the user. Since (Yjv + Yiv £ 1), then constraints (5.a)-(5.b) and (8.a)-(8.b) can be eliminated. The value of dmax should be carefully chosen in such a way that a significant number of non-optimal routes could be eliminated without removing the optimum from the problem feasible region.
- A node i cannot be assigned to a far away depot. Then, the vehicle assigned to node i cannot be allocated to a depot that is far away from node i. This heuristic conditionally restricts the set of potential depots for a vehicle accounting for the route assigned to it. This condition can be so written: ![]() (22)
(22)
Then, constraints (4), (6), (7) and (9) can be eliminated.
C. The multi-heuristic case
Since the simultaneous use of several rules can either eliminate the problem optimal solution or generate redundant constraints of the type Yiv + Yjv £ 1, the heuristics must sequentially be applied in a hierarchical way. Distance-based heuristics must first be enforced before using the exact time window-based elimination rules, since the former ones remove routes from the problem formulation while the others just take away and/or simplify sequencing constraints.
VI. EXAMPLE 2
Example 1 is revisited to now regard time-windows and maximum routing time as soft constraints that may be violated. Such violations will be penalized and, consequently, the objective function (13) is being adopted. In order to generate routing time constraint violations, the maximum allowed routing time was reduced to tvvmax = 3.0. Table 4 presents the new optimal solution. In turn, Table 3 shows the problem size and the computational requirement with/without applying distance-based and time window-based elimination rules.
It can be observed a significant reduction in the CPU time with regards to the classical formulation by a factor larger than 500 without using elimination rules and by 10,000 times with elimination rules. Savings in 0-1 variables and in CPU time are mostly brought about by the exact TW-based elimination rules. The distance-based heuristic rules cut the CPU time down by half but the optimal solution is still found (see Table 4).
Table 3. Computational requirements and models sizes for Examples 1 & 2
Table 4. Optimal solution for Example 2
VII. CONCLUSIONS
A novel continuous-time MILP formulation for the VRPTW problem based on the generalized precedence notion has been developed. In the proposed approach, a node precedes another one on the route if it is visited earlier by the same vehicle, but not necessarily immediately before. This allows to separately treating assignment and sequencin decisions through different sets of 0-1 variables. By so doing, a remarkable saving in binary variables is obtained. The proposed model is also capable of handling hard and soft time window constraints. The use of exact time window-based elimination permits to get an important additional reduction in the number of sequencing variables and constraints. Numerical experiments show very encouraging results.
NOMENCLATURE
Sets
![]()
Parameters

Variables

REFERENCES
Bodin, L., Golden, B., Assad, A., Ball, M., "Routing and Scheduling of Vehicles and Crews: The State of the Art", Comput. & Oper. Res., 10. 2, 62-212 (1983). [ Links ]
Desrochers, M., Desrosiers, J., Solomon, M., "A New Optimization Algorithm for Vehicle Routing Problem With Time Windows", Oper. Res., 40, 342-354 (1992). [ Links ]
Desrosiers, J., Dumas, Y., Solomon, M., Soumis, F., "Time Constrained Routing and Scheduling". Handbook in Operations Research and Management Science, 8 Network Routing, 35-139. North-Holland, Amsterdam (1995). [ Links ]
Fisher, M., Jornsten, K., Madsen, O., "Vehicle Routing With Time Windows: Two Optimization Algorithms", Oper. Res., 45, 488-495 (1997). [ Links ]
ILOG OPL Studio 2.1., User´s Manual. ILOG S.A. France (1999). [ Links ]
Kolen, A., Rinnoy, K. A., Trienkens, H., "Vehicle Routing With Time Windows", Oper. Res., 35, 266-273 (1987). [ Links ]
Received: September 16, 2001.
Accepted for publication: September 17, 2002.
Recommended by Guest Editors S. Díaz and A. Bandoni.














