Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.33 n.3 Bahía Blanca jul./sept. 2003
Regional risk associated with the transport of hazardous materials
L. Nardini1, L. Aparicio2, A. Bandoni3 and S. M. Tonelli4 *
1 CIC – FUNDASUR (Fundación del Sur para el Desarrollo Tecnológico)
2 FUNDASUR – APELL Bahía Blanca
3 PLAPIQUI (Planta Piloto de Ingeniería Química)/CONICET
4 PLAPIQUI/CONICET – FUNDASUR
PLAPIQUI, Camino "La Carrindanga" Km 7 (8000) Bahía Blanca, Argentina
FUNDASUR, 12 de Octubre 1842, (8000) Bahía Blanca, Argentina
{lnardini, laparicio, abandoni, stonelli}@plapiqui.edu.ar
Abstract ¾ An increasing concern over the level of risk associated with hazardous materials transportation has led international efforts to focus on risk assessment at regional level. Following this trend, the aim of this work is to review the latest procedures for analysing the regional risks resulting from hazardous materials transportation by means of road and rail. In particular, two methodologies are reviewed and discussed, a method recently developed at Swiss Federal Institute of Technology [1] and the strategy outlined by CCPS [2]. The extent of these methodologies has been explored in order to find their advantages and disadvantages.
As a case study this paper considers the transport of methanol from its production site to the port where it is going to be stored, obtaining risk results using at least one of the above mentioned methodologies.
Keywords ¾ Risk Analysis. Hazardous Materials. Transport.
* To whom all correspondence should be addressed
I. INTRODUCTION
Assessing the risk of a region implies the use of a complex methodology, requiring information about hazards to health and environment. In particular, special attention has to be paid to potential risks arisen from the transport of hazardous materials (HAZMAT) through large territorial areas which, in some cases, are heavily populated.
Actual or potential incidents in transport and distribution of hazardous substances could result in death or injury to people, property damage, or damage to the biophysical environment, through the effects of fire, explosion or toxicity. An increasing number of transportation accidents involving dangerous substances have occurred world–wide, giving place to major awareness in government, industry and community in topics that have to do with safety management of hazardous materials transportation.
Transportation Risk Analysis (TRA) is quite similar to risk analysis in fixed facilities and makes it possible to manage and control transport risks by determining the most sensitive parameters as well as to identify and evaluate risk reduction strategies and alternatives. TRA can be conducted on a qualitative or quantitative basis calculating relative or absolute risk indexes, depending on both the information available and the purpose of the study. The present paper will focus on methodologies developed to perform quantitative studies.
In this scope, the methodology recently developed at Swiss Federal Institute of Technology (Nicolet-Monnier and Gheorghe, 1996) and the strategy outlined by CCPS (1995) are studied, leading to the estimation of individual and societal risk. The main procedural steps related to quantitative risk analysis for transportation systems are supported by the foregoing developed methods for fixed installations. Special attention is also given to how to gather local information and to estimate coefficients that reflect the conditions prevailing in the region considered in the case study presented.
II. CCPS METHODOLOGY
To perform a TRA analysis, CCPS suggests some basic steps to take into account all the representative factors that affect the risk over a route where it is being transported a certain amount of a hazardous substance: 1) Movement Description; 2) Hazards or Initiating Events Identification; 3) Incident Enumeration; 4) Selection of Significant Scenarios; 5) Consequence Estimation; 6) Likelihood Estimation; 7) Risk Estimation; 8) Utilisation of Results.
A. Route Segmentation and Frequency Analysis
The way characteristics (population density, weather conditions, topography, accident frequencies, etc.) could vary very much from point to point, so the route should be divided in sections having similar features. This helps to assign the proper conditions to each portion of route, making the study more rigorous.
The global chance of release is calculated separately for the various sections of the route and later, probabilities are assigned to each proposed scenario considering if routes are over urban, suburban or rural areas.
The frequency of overall release over a railroad section is calculated as follows:
RFtrain = TAR x LS x NC x DP x RP (1)
For truck release frequencies, it is used:
RFtruck = AR x LS + NIR x OH (2)
The second term in the last equation represents incidents that come from events not initiated by accidents. A fault analysis (e.g. HAZOP techniques) should be made to identify potential sources of equipment damages and releases, i.e. mechanical failures, corrosion, human errors, bad maintenance, etc.
B. TRA Consequence Analysis
Consequence analyses can be made nowadays with specific software, which include different source, dispersion and effect models in their structure. All possible scenarios must be defined, which include information about the material release and the conditions at which it is being transported, the type of rupture and the characteristics of the route section (rural or urban, weather conditions, etc).
Depending on the objective of the specific work, a damage criterion has to be fixed, i.e. people death, severe injuries, property damages, etc., so the correspondent radiation, overpressure and toxic levels are used. The simulation result will be the distance where exposed people will suffer the consequences determined by the criterion selected. Then, the quantity of people involved in each of the analysed scenarios (calculated as % of people affected) can be determined by vulnerability studies.
C. Risk Calculation
Different measures of risk are defined according to the way that magnitude and likelihood of damages are related to each other. The most common indexes are:
Individual risk: considers the risk to an individual who may be in the effect zone of an incident or set of incidents. This index can be drawn as individual risk contours, average individual risk plots, etc.. The size of the incident, in terms of the number of people impacted by a single event, does not affect individual risk.
Societal risk: estimates the risk to a group of people located in the effect zone of an incident or set of incidents, normally is represented by the Frequency-Number (F-N) curve.
III. BUWAL METHODOLOGY
This methodology has been applied to specific cases in Switzerland, but its outlines could be helpful to analyse the risks in transport movements in other countries, considering their own features.
A. Estimation of Transport Accidents Probabilities
As in the previous methodology, the route is segmented to consider the variation of the characteristics along each way section. The frequency of representative scenarios is determined for each road section as:
Fs = ADT x 365 x HTS x AR x SDH x RSC x RRP x RRI x RSS (3)
Frequencies of railroad representative incident scenarios are calculated as:
Fs = YDG x AR x PD x RRI x RSS (4)
where PD= 4 (nDG / nG)
B. Estimation of Consequences and Risk Calculation
Results obtained from Section II.B and outlines for risk indexes calculation in Section II.C can be used in the framework of this methodology to estimate the regional risk level.
C. Comparison of alternate routes
BUWAL methodology outlines a short-cut approach useful when two alternate routes want to be compared for the same product and quantity transportation, or when two different cargoes must be compared for the same route.
The probable number of fatalities from the passage of a tank/wagon carrying a load L along the entire length of the route can be calculated, for both modes of transport, as:
SIL S i Pai Di (5)
where SIL = S j p rj2 Psj
For any given load, it is possible to compare the relative safety of two alternative routes by examining Pai Di. Thus, smaller values of this term indicate safer transport operations. For any given route, the safety of two alternate cargoes can be compare by observing SIL As in the previous case, the smaller the safer.
IV. CASE STUDY
A. Description
This case involves a weekly movement of 10800 m3 of methanol through an approximate 700 km-length route. A traditional risk analysis was made for the cases of road and rail transport, calculating risk indexes.
Information of train movements is extracted from real operation (216 wagons/week). A similar weekly movement was ideated for road transport (324 trucks/week), according to real rail tanks and standard truck tanks characteristics summarised in Table 1.
Route sections were defined based on population densities and weather conditions. Both routes have similar layout, so an equal segmentation was assumed for road and railroad transport (see Table 2). Geographical locations are sketched in Fig. 1.
Table 1. Substance and Tanks Characteristics

Fig 1. Road and Rail Routes Segmentation
Table 2. Segmentation of Routes

B. Hazardous Materials Accidents Statistics
Analysis of historical data is the most suitable information for a TRA. Thus, to gather real accident frequencies concerning the region being analysed, the National Transport Regulatory Commission (CNRT) was consulted, but due to the small quantity of major accidents registered, estimation of accident rates is not statistically valid and can lead to wrong evaluations. For this reason international information was consulted.
Calculations were based on the following data from Italy and The Netherlandss statistics (Nicolet-Monnier and Gheorghe, 1996, Mazzarotta, 2001, Gataola, 2001):
Train Incidents: 4.3 x 10-7 accidents/train-km-yr.
A percentage of 13,6% corresponds to releases of dangerous goods; and over this value, 90% leads to a continuous release and 10% to loss of the entire contents.
Truck Incidents: 4.0 x 10-8 accidents/truck-km-yr.
A percentage of 13.8% corresponds to releases of hazardous materials; a 97% leads to a continuous release and 3% to loss of the entire contents.
The above values lead to think of trucks as safer means of transport than trains. Nevertheless, this does not necessarily imply that road transport is safer, since, in order to risk evaluation, not only incident frequencies have to be considered but also incident consequences.
C. Selection of Scenarios
To select representative scenarios, the following characteristics were assumed:
- The substance under scope is flammable (UFL= 360000 ppm, LFL=73000 ppm) and has a certain level of toxicity, so consequences of fire, dispersion and explosion events were considered (CCPS, 2000).
- Two basic scenarios were analysed: a continuous loss of 1% of contents per minute and a total release.
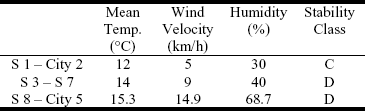
- Routes were divided in three parts, and three different weather conditions were assigned, one for each part. For the last portion, corresponding to the area of Bahía Blanca and previous cities, the most characteristic weather condition was extracted from a special study made for this region a few years ago. If possible, the worst atmospheric condition should be taken into account to make the study conservative.
Table 3. Most Characteristic Weather Conditions
- Only derailments and collisions were considered for train and truck accidents respectively. Non-accident initiated incidents were not considered due to lack of information in this field (HAZOP techniques or similar studies should be necessary to complement this and to identify potential sources of damages).
- Derailment of one wagon per train per accident was considered, avoiding the possibility of domino effect.
- Incident outcomes considered in this analysis were generated by means of an event tree for each release case.
D. Consequence Calculation
Levels of radiation, toxic concentration and overpressure were determined for two different criteria: fatalities (F) and severe damages (SD) to exposed people. The values assumed are: toxicity concentration F=25000 ppm and SD=2500 ppm; radiation F=37.5 kW/m2 and SD=12.5 kW/m2; overpressure F=2.23 atm. and SD=2.11 atm.
The commercial software SuperChems (Little, 1997) was used to perform the consequence analysis. Distances obtained from this analysis were utilised as radii to determine the hazard areas for each scenario. The possible outcomes for both continuos and total releases resulted to be Early and Late Pool Fire, Flashfire, and Toxic Dispersion. Explosion was finally not considered because, the consequence analysis proved that overpressure levels for fatalities and severe damages were not reached. In order to estimate social risk, a 100% of affected people was considered, i.e. all people in the hazard area were "touched" by the effects.
The consequences for rail transport, for both criteria, were more severe than for road transport. These results were expected because rail tank contains a larger amount of product.
E. Results
CCPS and BUWAL methodologies were implemented in order to determine different risk indices for the case proposed. The second one could not be strictly applied because of lack of dissociated information (e.g., RRP, RSS, RRI, etc.). Observing the terms of the expressions for frequency estimations it can be seen that, associating factors, the same results and units can be obtained for both methodologies. With the available information at this stage, equal accident frequencies were obtained by the mentioned methods.
Consequence results were combined with the accident frequency to obtain different risk measures:
Societal Risk: The Frequency-Number (F-N) curves were considered in representation of societal risk. These curves plot cumulative frequency versus a number of fatalities and give a picture of the overall risk along each route. Each risk estimate is calculated by summing the frequencies for all incident outcome cases (Fi) that yield an indicated number of fatalities (N) or greater (Ni³ N) . This can be expressed as:
FN = S i Fi (6)
Figures 2 and 3 show the calculated F-N curves for both rail and road routes outlines, considering fatalities and severe damages criteria. These results are compared with the limits imposed to the social risk related to road and rail hazardous materials transportation (ACDS, 1991). The upper line is the tolerability line. Risks above this line are regarded as intolerable. The bottom line is the negligible risk line and risks below it are regarded as negligible. Risks located between the upper line and an intermediate line (called the scrutiny line) may be unjustifiable and require further study. It is important to point out that these limits only correspond to risks associated to fatalities; thus, curves representing severe damages should not be compared to these lines.
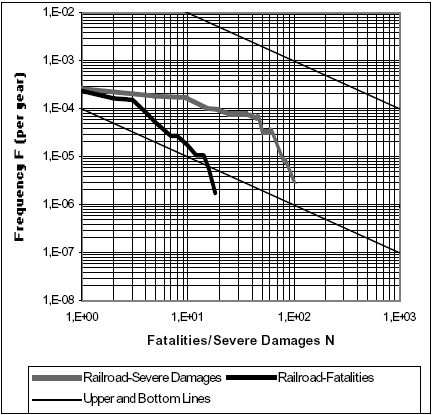
Fig. 2. F-N Curves for Methanol Railroad Transportation
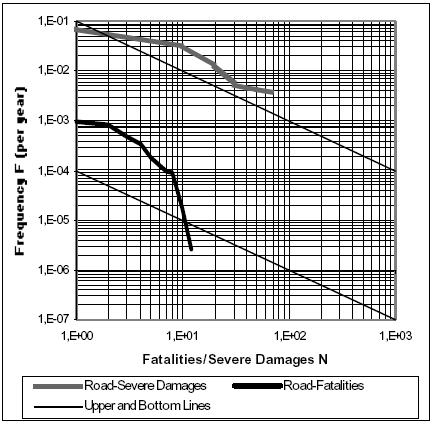
Fig. 3. F-N Curves for Methanol Road Transportation
Individual Risk: Results obtained for calculation of individual risk indexes are shown using the average individual risk (AIR) and individual risk profiles (IRP).
For AIR calculations, the products of each frequency/consequence pair are summed and the result is divided by the total population of concern:
AIR = S in Fi . Ni / PT (7)
where n represents the number of scenarios.
IRP representations consist in a graphic where x axis corresponds to the distance from the source, and y axis is assigned to the cumulative frequency of scenarios which effects reach the considered x distance.
In AIR estimations the total population of concern was calculated over the overall length of route. For each section, the maximum distance related to the worst scenario was multiplied by two (to consider both sides of the route) and by the corresponding population density. These results were summed to yield the total population of concern.
The average individual risk results, based only on fatalities, are: 1.858 10-7/yr for railroad transport and 7.783 10-7/yr for road transport.

Fig. 4. IRPs for Railroad Transportation

Fig. 5. IRPs for Road Transportation
IRPs were calculated for each section both for rail and road transportation. The three most relevant sections (City 1, City 3 and City 5) were selected, and their individual risk profiles plotted. It is important to notice that the selected sections differ in the weather conditions assumed for consequence calculation, as well as in their length and population density, but all of them correspond to an urban area.
The two sets of curves generated by means of this analysis are shown in Fig. 4 and 5, for rail and road transport, respectively. In these figures it can be observed that beyond certain distances from de source, the lines corresponding to different sections are interrupted. This is because there are no scenarios with effects exceeding that distance.
A specific level of 1x10-6 /yr is considered as "broadly acceptable" (Lees, 1996) and was used to compare individual risks.
V. CONCLUSIONS
Comparing both methodologies and assuming all the required information is available, BUWAL Methodology seems to be more rigorous, as shown in accidents frequency expressions where factors are more specific than those in CCPS expressions. Nevertheless, so detailed information is not easily available, even in developed countries such as Canada, USA and European Union, making this characteristic a relative advantage.
In these two TRA methodologies, as in all those related to risk analysis, it was found a strong dependence between results and parameters. Thus, if decisions must be taken about alternate routes or modes of transport, emergency planning, etc., local information must be used in order to obtain results as realistic as possible.
For the case study analysed in this work, the same results were virtually obtained for BUWAL and CCPS methodologies. This is because due to the lack of dissociated information required for BUWAL it was necessary to combine terms in accident frequency expressions and it resulted to be, jointly, a similar equation as for CCPS.
Accident frequency was estimated from international data since the gathered local information (consulted to CNRT) was not statistically valid. Therefore, values obtained from Italy and The Netherlands were used in the analysis.
With respect to the alternate means of transport, results prove that rail transport is safer than road transport, as expected. It should be highlighted again the importance of the risk indices evaluation as a combination of scenario consequences and probabilities of occurrence, because the independent analysis of them could lead to incorrect conclusions. This fact can be observed in results informed in Sections IV.B and IV.D.
F-N curves show that for both criteria, fatality and severe damage, rail transportation is safer than road. This is due to the frequency at which incidents with a certain number of affected people occur is rather lower for trains than for trucks. As risk values change basically according to accident indexes, special attention must be paid in its calculation. Besides, consistency between railroad and road accident indexes information is essential when these two transport means are being compared, i.e. both from local or both from international source.
Comparing the curves obtained with the upper and bottom line of the acceptable and unacceptable limits, Fig. 2 demonstrate that for this particular case, rail transportation risk curve falls into the region considered as tolerable, moreover, it is rather far from the intolerable space. By the other hand, in Fig. 3 the fatality curve is almost in the middle of the tolerable region, but closer to the upper line than curve that corresponds for train transport.
Moreover, both AIR and the IRPs also prove that the train is the safest option. Acceptable AIRs values were obtained, less than 1.10-6 /yr. IRPs show that a person living 50 m. from the accident source is almost completely out of danger and, as expected, being closer to the source involves a higher risk.
NOTATION
ADT: Average Daily Traffic (total vehicles/day-km).
AR: Accidents Rate
(year-km)-1 in Equation (2);
(vehicle-km)-1 in Equation (3);
(rail wagons-km)-1 in Equation (4).
CNRT: National Transport Regulatory Commission.
DP: Derailment Probability (dimensionless).
Di: Population density in section i (inhabitants/km2).
Fi: Frequency of incident outcome case i (year-1).
FN: Frequency of all incident outcome cases affecting N or more people (year-1).
Fs: Scenarios Frequencies (km-year)-1.
HTS: Heavy Traffic Share based on Average Daily Traffic (dimensionless).
LFL: Lower Flammability Level.
LS: Length of Section (km).
nDG: Number of Wagons transporting Dangerous Goods.
nG: Average Number of Wagons in the train.
NC: Number of cars shipped per train.
NIR: Non-accident Incidents Rate (hr-1).
OH: Number of Operating Hours (hr/year).
PD: Probability of Derailment or Collision (dimensionless).
Pai: Probability of the tanker of being involved in an accident in section i (dimensionless).
Psj: Probability of scenario js occurrence (dimensionless).
PT: Total Population of concern (inhabitants).
rj: Effect radius of scenario j (km).
RF: Release Frequency (year-1).
RP: Release Probability (dimensionless).
RRI: Release or Ignition Probability (dimensionless).
RRP: Probability of relevant products applicable to representative incident scenarios (dimensionless).
RSC: Probability of presence of Hazardous Materials (dimensionless).
RSS: Probability of Severe Consequences Scenarios (dimensionless).
SIL: Severity Index for a specific load L.
SDH: Ratio of Dangerous Goods traffic based on the Heavy Traffic (dimensionless).
TAR: Train Accident Rate (year-km-car)-1.
UFL: Upper Flammability Level.
YDG: Yearly average number of Goods trains transporting Dangerous goods (rail wagons/year).
Acknowledgements
Authors are grateful to Mr. Julio Giambelluca for providing useful information, and also wish to acknowledge the financial support received by CONICET, FUNDASUR and APELL-Bahía Blanca.
REFERENCES
1. ACDS Advisory Committee on Transport of Dangerous Substances. Transport Hazard Report. (1991). [ Links ]
2. CCPS "Guidelines for Chemical Transportation Risk Analysis". AIChE. New York. (1995). [ Links ]
3. CCPS "Guidelines for Chemical Process Quantitative Risk Analysis". AIChE. New York. (2000). [ Links ]
4. Gataola, E., "Why are Transport-Risk Analyses Wrong? - Part I", Proc. ESREL 2001, Torino, Italy, 71-78 (2001). [ Links ]
5. INDEC National Census 1991. (1991). [ Links ]
6. Lees, Frank P. "Loss Prevention in the Process Industries: Hazard Identification, Assessment and Control." Second Edition. Butterworth-Heinemann. (1996). [ Links ]
7. Little, A.D., "SuperChems User´s Guide". Massachusetts. USA. (1997). [ Links ]
8. Mazzarotta, B., "Risk Reduction when Transporting Dangerous Goods: Road or Rail?", Proc. ESREL 2001, Torino, Italy, 637-644 (2001). [ Links ]
9. Nicolet-Monnier, M. & Gheorghe, A. "Quantitative Risk Assessment of Hazardous Materials Transport Systems". Kluwer Academic Publishers. The Netherlands. (1996). [ Links ]














