Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.33 n.3 Bahía Blanca jul./sept. 2003
Phase equilibria for quaternary mixtures in esterification reaction systems
E. A. Campanella* and B. A. Mandagaran
Instituto de Desarrollo Tecnológico para la Industria Química
(Universidad Nacional del Litoral – CONICET)
Güemes 3450 – 3000 Santa Fe – Argentina
tquique@ceride.gov.ar
Abstract ¾ This paper examines the effect of the simultaneous chemical and phase equilibrium on the conceptual design of reactive distillation processes. Esterification of acetic acid with methanol, ethanol and butanol are examined. Using commercial software, azeotropic points, residue curve maps and distillation line diagrams having been calculated. The analyzed systems have showed different behavior when phase equilibrium parameters and chemical equilibrium constants are changed. The methyl acetate system does not change the topological features of residue curve maps and distillation line diagrams. The ethyl acetate system and the butyl acetate system change the topological features of the graphs when different chemical equilibrium constants are used.
Keywords ¾ Phase Equilibrium. Chemical Equilibrium. Reactive Systems. Esterification. Reactive Distillation.
* Author to whom correspondence should be addressed.
I. INTRODUCTION
In the last decade, reactive distillation has become an important alternative to the usual reaction separation processes. Agreda et al. (1990), Doherty and Buzad (1992) have described the advantages of reactive distillation in industrial applications. Other authors have considered different aspects of the reactive distillation. In particular, Doherty (Barbosa and Doherty 1988a, 1988b; Okasinski and Doherty, 1997, Chadda et al., 2000) has examined the most relevant aspects of reactive distillation for the design of distillation sequences and columns. The first step of almost all design methods is an analysis of feasibility where residue curve maps or distillation line diagrams are very useful. An important point in analyzing reactive distillation feasibility is the influence of the chemical reaction and the phase equilibrium on residue curve maps and distillation line diagrams. The effect of property inaccuracies on process design has been reported earlier by Streich and Kistenmacher (1979), Nelson et al. (1983) and Hernandez et al. (1984). Studies that are more recent have analyzed the effect of model (Mandagarán et al., 1999) and of thermodynamic data (Whiting et al., 1999) on calculated process performance. Okasinski and Doherty (1997) explored the effect of the reaction equilibrium constant on the existence and location of reactive azeotropes for chemical equilibrium systems with a single chemical reaction. However, the combined effect of phase equilibrium and chemical equilibrium on reactive distillation have not been analyzed.
In this work, we present calculations to study the effect of phase and chemical equilibria on residue curve maps and distillation line diagrams for three esterification systems: methyl acetate, ethyl acetate and butyl acetate.
II. Calculation Description
In a residue curve map or in a distillation line diagram, pure component boiling points and azeotropic points are nodes (stables or unstables) or saddle points that set the topological feature of the graph. In this work, non-reactive systems are examined through residue curve maps, and reactive systems are looked through distillation line diagrams. The two graphs are necessary since reactive distillation is normally a sequence that involves separation with and without reaction.
The non-reactive azeotropy conditions are the equality of molar fraction for each component in the vapor phase and in the liquid phase. At a reactive azeotrope, the change in composition due to reaction is compensated by the change in composition due to phase equilibrium, and so a constant boiling mixture is achieved. For the esterification systems in this work (four component mixture involving one independent reaction) a convenient way to represent the reactive azeotropy condition is (Ung and Doherty, 1995).
Xi = Yi, i = 1,...,3 (1)
where Xi and Yi are a set of transformed mole fraction variables in the liquid phase and vapor phase respectively. The transformed mole fractions for acetic acid (AA), the alcohol (OH), the ester (AC) and water (W) are given as
XAA = xAA + xAC (2)
YAA = yAA + yAC (2')
XOH = xOH + xAC (3)
YOH = yOH + yAC (3')
XW = xW - xAC (4)
YW = yW - yAC (4')
where the x and y are the actual mole fractions of component i in the liquid and vapor phases. At a reactive azeotrope, both phase and reaction equilibrium conditions must be satisfied. The thermodynamic definition of the reaction equilibrium constant is given by
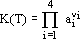 | (5) |
ai = xi gi, i = 1,....4 (6)
where ai is the activity of component i in the liquid phase and gi is the activity coefficient.
In this work the calculations were done in two stages: first we found the azeotropic points, and second we built the residue curve map or the distillation lines diagram. To do the calculation we have used commercial software: DISTIL and HYSYS (Hyprotech, 2001). We wrote using the Macro Language Editor of HYSYS two programs. The azeotropic points, in particular the reactive azeotropes, were calculated with one of those programs. The other program built the distillation line diagram in EXCEL. After picking up a set of equilibrium phase parameters and a chemical equilibrium constant we changed theirs values and examined the different graphs comparing their topological features. The changes that we did were in the order of the experimental uncertainties.
III. RESULTS AND DISCUSSION
Three esterification systems have been studied: a system without reactive azeotrope (methyl acetate), a system with a homogeneous reactive azeotrope (ethyl acetate), and a system with a heterogeneous reactive azeotrope (the butyl acetate). In this work, we present results using the UNIQUAC (Prausnitz et al., 1999) model for the activity coefficients. We also did calculations using WILSON (Prausnitz et al., 1999) and NRTL (Prausnitz et al., 1999) obtaining identical results that with UNIQUAC. Vapor phase behavior was model using the virial equation of state (Hayden-OConnell, 1975). The model equations used are listed in the Appendix A.
A. Methyl acetate system
The esterification of acetic acid (AA) with methanol (MeOH) produces methyl acetate (MA) and water (W) as shown in the equation
C2H4O2 + CH4O = C3H6O2 + H2O (7)
The system is assumed isobaric at atmospheric pressure and the thermodynamic properties are listed in Table 1. The non-reactive system has four pure components and two minimum-boiling homogeneous azeotropes: (W-MA) and (MeOH-MA). All those points are marked in Figure 1. The plot shows a few residue curves to indicate the existence of only one distillation region. On the other hand Figure 2, where the composition space in chemical equilibrium is represented in the transformed coordinates of Ung and Doherty ( 1995), displays a few distillation lines for the reactive system. The chemical equilibrium constant varies over a range of values (10 to 50) as determined experimentally by Song et al. (1998) and Pöpken et al. (2000). Figure 2 shows distillation lines using Pöpken et al. data for the equilibrium constant. We have used UNIQUAC parameters from HYSYS and they are shown in Table 1. Those parameters gave good agreement against selected experimental data: below 0.015 for absolute error in vapor molar fraction, 1.00 for absolute error in temperature in the binary systems, below 0.04 for absolute error in vapor molar fraction, 2.00 for absolute error in temperature in the ternary systems and in the quaternary system (without reaction). As shown in Figure 2 the methyl acetate system lacks a reactive azeotrope. Figure 1 and 2 show that there is only one distillation region in both systems: reactive and non-reactive. As we changed the UNIQUAC parameters and the chemical equilibrium constant the topological features of the distillation line diagram and the residue curve map did not change.
The UNIQUAC parameters were changed in a way that represents experimental uncertainty. The two binary systems that exhibit azeotropic behavior were chosen and two different sets of experiments were used for each binary system to get the UNIQUAC binary parameters. For the chemical equilibrium constant two additional values were chosen to represent the experimental uncertainty. In summary, we introduced three factors (water-methyl acetate vapor-liquid data, methanol-methyl acetate vapor-liquid data, chemical equilibrium constant) to determine their effect on the non-reactive residue curves and on the reactive distillation lines. Each factor was considered at two levels (+ and -) and we combined them in a factorial way representing nine combinations including the original setting. Table 2 presents the calculated non-reactive azeotropes using only one level for the chemical equilibrium constant. Results with the other level for the constant are similar. Calculations did not show the presence of a reactive azeotrope in any factor combination. From Table 2 it is possible to see that all the factor combinations gives the same behavior that the one shown in Figure 1 and 2 belonging to the original parameter setting. For any combination of vapor-liquid binary parameters and chemical equilibrium constant, there is only one distillation region for the non-reactive and reactive system, and there is very little difference between the calculated azeotropes.
Table 1. Thermodynamic data for the methyl acetate system.
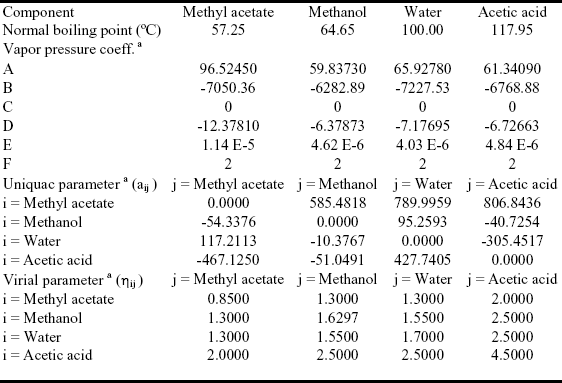
a) see Appendix A.
Table 2. Results for the methyl acetate system.
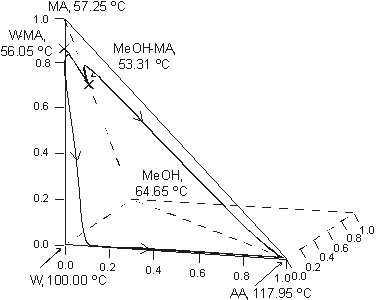
Fig. 1. Residue curve map for the methylacetate system. AA, acetic acid; MeOH, methanol; MA, methylacetate; W, water.
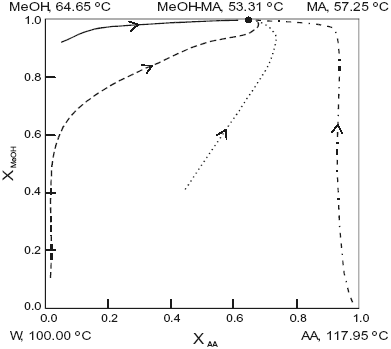
Fig. 2. Distillation line diagram for the esterification of methanol. Ln K = 1.367 + 682 / T (K). AA, acetic acid; MeOH, methanol; MA, methylacetate; W, water. Xi , transformed compositions (eqn.2 and 3).
B. Ethyl acetate system
The esterification of acetic acid (AA) with ethanol (EtOH) produces ethyl acetate (EA) and water (W) as shown in the equation
C2H4O2 + C2H6O = C4H8O2 + H2O (8)
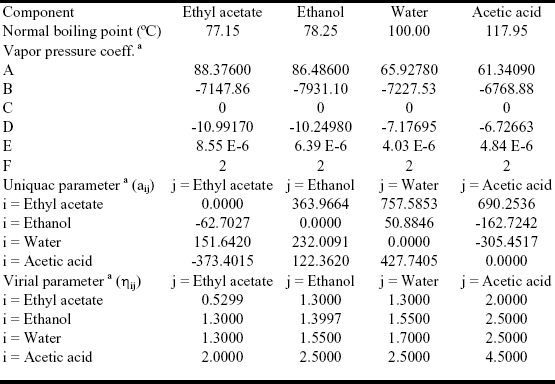
The system is assumed isobaric at atmospheric pressure and the thermodynamic properties are listed in Table 3. The non-reactive system has four pure component, two minimun-boiling homogeneous azeotropes: (W-EtOH) and (EtOH-EA), one minimun-boiling heterogeneous azeotrope (W-EA), one minimun-boiling heterogeneous ternary azeotrope (EtOH-EA-W). All those points are marked in Figure 3. The plot shows a few residues curves to indicate the existence of only one distillation region. The distillation lines of the reactive system is presented in Figure 4, a few lines are drawn. Okasinski and Doherty (1997) reported a wide range of chemical equilibrium constant values (0.25 to 14.5). We have used a chemical equilibrium constant of 13.4 as reported by Kang et al. (1992), and UNIQUAC parameters from HYSYS (Table 3). Those parameters gave a reasonable agreement against selected experimental data: below 0.02 for absolute error in vapor molar fraction, below 0.5 for absolute error in temperature for the binary systems (with exception of water-ethylacetate with 0.07 and 2.15); below 0.015 in vapor molar fraction and 1.3 in temperature for the W-EA-EtOH ternary system; and the correct shape for the binary and ternary liquid-liquid equilibria. Figure 4 shows that the system has no reactive azeotrope and only one distillation region. The existence of the reactive azeotrope is depending of the value of the chemical equilibrium constant, but it is not depending of the values of the phase equilibrium parameters.
As in the methyl acetate system we changed UNIQUAC parameters, here to take in account not only the experimental uncertainty but to consider also a different kind of data. We considered ternary vapor-liquid equilibrium for the water-ethylacetate-ethanol system at two levels belonging to two different sets of experimental data. This factor, ternary information, proved to be a major influence. As the ternary data involve binary parameters for all the binary systems of the ternary mixture, the calculated azeotropes, liquid-liquid equilibria, distillation lines and residue curves changed. The non-reactive system displayed two distillation regions and a reactive azeotrope appeared rising the distillation region to two when the reaction was considered. Table 4 presents the calculated non-reactive and reactive azeotropes when two factors, EtOH-EA vapor-liquid equilibrium and chemical equilibrium constant, were studied at two levels (+ and -).
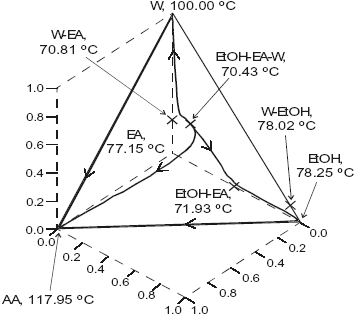
Fig. 3. Residue curve map for the ethylacetate system. AA, acetic acid; EtOH, ethanol; EA, ethylacetate; W, water.
Table 3. Thermodynamic data for the ethyl acetate system.
a) see Appendix A.
Table 4. Results for the ethyl acetate system.
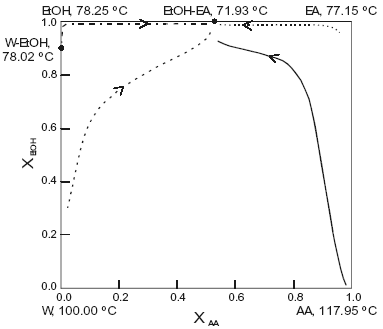
Fig. 4. Distillation line diagram for the esterification of ethanol. AA, acetic acid; EtOH, ethanol; EA, ethylacetate; W, water. Xi , transformed compositions (eqn.2 and 3).
As seen from the table the EtOH-EA factor does not change anything, on the contrary the chemical equilibrium constant factor allows the presence of a reactive azeotrope changing the topological features of the distillation line diagram with two distillation regions.
C. Butyl acetate system
The esterification of acetic acid (AA) with n-butanol (BuOH) produces butyl acetate (BA) and water (W) as shown in the equation
C2H4O2+C4H10O=C6H12O2+H2O (9)
The system is assumed isobaric at atmospheric pressure and the thermodynamic properties are listed in Table 5. The non-reactive system has four pure components, one minimum-boiling homogeneous binary azeotrope (BuOH-BA), two minimun-boiling heterogeneous binary azeotropes (W-BuOH) and (W-BA), one maximun-boiling homogeneous binary azeotrope (AA-BuOH), one intermediate-boiling homogeneous ternary azeotrope (BuOH-AA-BA) and one minimun-boiling heterogeneous ternary azeotrope (W-BuOH-BA). These points are marked in Figure 5. The plot shows a few residue curves to indicate the existence of two distillation region. In one of them, residue curves start at the heterogeneous W-BuOH-BA ternary azeotrope and end at the AA-BuOH binary azeotrope. In the other region, residue curves start at the same ternary azeotrope and end at the pure butyl acetate. On the other hand, Figure 6 displays a distillation line diagram using the transformed coordinates for the reactive system. We used a chemical equilibrium constant of 12.5 as reported by Venimadhavan et al. (1999), and UNIQUAC parameters from HYSYS (Table 5). Those parameters gave a good agreement against selected experimental data: below 0.025 for the absolute error in vapor molar fraction, 1.00 for the absolute error in temperature in the binary systems and the correct shape for the binary and ternary liquid-liquid equilibria. Figure 6 shows that the system has a reactive azeotrope. A quaternary reactive azeotrope appeared between the W-BuOH azeotrope and the W-BuOH-BA azeotrope inside the two liquid phase zone. Then, the azeotrope is a heterogeneous reactive azeotrope and a stable node of the diagram where all distillation lines end. The plot shows two distillation regions, one starting at pure butyl acetate and the other at pure butanol. The two regions are due to the existence of the BuOH-BA binary azeotrope. When we changed the UNIQUAC parameters and the chemical equilibrium constant, the topological features of the distillation line diagram changed.
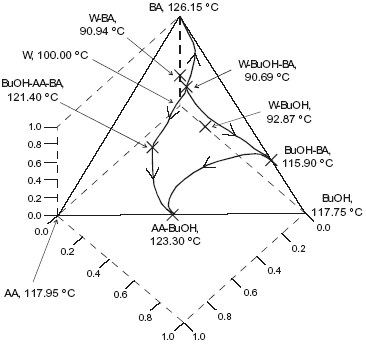
Fig. 5. Residue curve map for the butylacetate system. AA, acetic acid; BuOH, n-butanol; BA, butylacetate; W, water.
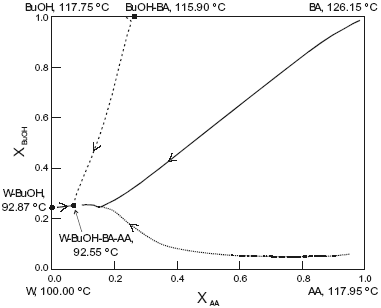
Fig. 6. Distillation line diagram for the esterification of n-butanol. AA, acetic acid; BuOH, n-butanol; BA, butylacetate; W, water. Xi , transformed compositions (eqn.2 and 3).
Table 5. Thermodynamic data for the n-butyl acetate system.
Table 6. Results for the n-butyl acetate system.
Changes of uniquac binary parameters were introduced to consider the uncertainty in the heterogeneous W-BuOH binary azeotrope. As in the other systems, we have considered two levels (+ and -) for the UNIQUAC parameters and two levels (+ and -) for chemical equilibrium constant. Table 6 summarizes azeotrope calculations. It is possible to see that, when the chemical equilibrium constant has a value of six, the reactive azeotrope disappeared changing the topological features of the distillation line diagram. The changes in the two levels of the W-BuOH binary azeotrope did not modify the topological features of the residue curve map.
IV. CONCLUSIONS
In this work we have presented a simple analysis to see the effect of phase equilibria through activity coefficient model parameters and chemical equilibrium constant on the conceptual design of reactive distillation. The analysis is founded in azeotropic point determination, in residue curve map and distillation line diagram construction. The calculations were done using algorithms based in commercial software. The analyzed systems have shown different behavior when we changed UNIQUAC parameters and chemical equilibrium constants: the methyl acetate system does not change its topological features, the ethyl acetate system and the butyl acetate system change their topological features when different chemical equilibrium constants are used.
APPENDIX A. MODEL EQUATIONS.
A.1 Vapor pressure equation.
To model the temperature dependence of Pvap (T), a modified Antoine equation was used.
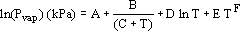 | (A - 1) |
The values of the coefficients A, B, C, D, E, F used in calculations are given in Tables 1, 3 and 5.
A.2 UNIQUAC equation.
To model liquid phase behavior, the UNIQUAC activity coefficient was used.
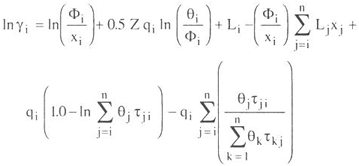 | (A - 2) | ||
| Lj = 0.5 Z (rj - qj) - rj + 1 | (A - 3) | ||
 | , | 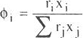 | (A - 4) |
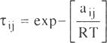 | (A - 5) | ||
where gi is the activity coefficient of component i, xi is the mole fraction of component i, T is the temperature, n is the total number of components, qi and ri are the area and volume parameters, Z the coordination number is set to 10.
The values of the energy parameters aij in cal/mol used in calculations are given in Tables 1, 3, and 5.
A.3 Virial equation.
To model vapor phase behavior, the Hayden-OConnell second virial equation was used. The chemical contribution of the equation is
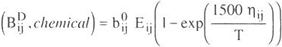 | (A - 6) |
with
 | (A - 7) |
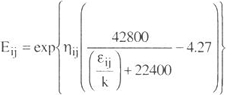 | (A - 8) |
where b0ij and eij / k are an equivalent hard-sphere volume and an energy parameter, hij is an association parameter for pure interactions and a solvation parameter for unlike interactions. The values of hij are given in Tables 1, 3 and 5.
NOTATION
| aij | UNIQUAC energy parameter |
| a | activity |
| K | chemical equilibrium constant |
| T | temperature |
| x | liquid mole fraction |
| X | transformed liquid mole fraction |
| y | vapor mole fraction |
| Y | transformed vapor mole fraction |
Greek letters
| hij | second virial association parameter |
| g | activity coefficient |
| v | stoichiometric coefficient |
Subscripts
| AA | acetic acid |
| AC | ester |
| i | component i |
| OH | alcohol |
| W | water |
Acknowledgements
The authors are thankful for the financial aid received from CONICET, UNL and ANPCyT.
REFERENCES
1. Agreda, V.H., Parin, L.H., Heise, W.H., "High purity methyl acetate via reactive distillation", Chem. Eng. Progr., 86, 40-46 (1990). [ Links ]
2. Barbosa, D., Doherty, M., "Design and minimun-reflux calculations for single-feed multicomponent reactive columns", Chem. Engng. Sci., 43, 1523-1537 (1988a). [ Links ]
3. Barbosa, D., Doherty, M., "Design and minimun-reflux calculations for double-feed multicomponent reactive columns", Chem. Engng. Sci., 43, 2377-2389 (1988b). [ Links ]
4. Chadda, N., Malone, M., Doherty, M., "Feasible products for kinetically controlled reactive distillation of ternary mixtures", AICHE J., 46, 923-936 (2000). [ Links ]
5. Doherty, M., Buzad, G., "Reactive distillation by design", Trans IchemE. W., 70 A, 448-458 (1992). [ Links ]
6. Gmehling, J., Onken, U., "Vapor-liquid equilibrium data collection", DECHEMA Chemistry Data Series, V. I, Part 1, DECHEMA, Frankfurt (1977a). [ Links ]
7. Gmehling, J., Onken, U., "Vapor-liquid equilibrium data collection", DECHEMA Chemistry Data Series,V. I, Part 2a, DECHEMA, Frankfurt (1977b). [ Links ]
8. Hernandez, M.R., Gani, R., Romagnoli, J.A., Brignole E.A, "The Prediction of Properties and its Influences on the Design and Modeling of Superfractionators", Proc. Second Int. Conf. on Foundations of Computer Aided Process Design (A.W. Westerberg and H.H. Chien Eds.) CACHE Pub, 709-740 (1984). [ Links ]
9. Hyprotech Ltd., HYSYS.Plant Dynamic Simulator, Optional modules: DISTIL (2001). [ Links ]
10. Kang, Y., Lee, Y., Lee, W., "Vapor-liquid equilibria with chemical reaction equilibrium - systems containing acetic acid, ethyl alcohol, water and ethyl acetate", J. Chem. Eng. Japan, 25, 649-655 (1992). [ Links ]
11. Lecat, M., "Tables azeotropiques", Monograph lauteur, Bruxelles (1949). [ Links ]
12. Mandagarán, B.A., Parodi, C.A., Campanella, E.A., "Azeotropic Distillation: Effect of the Thermodynamic Model", Latin American Applied Research, 29, 63-72 (1999). [ Links ]
13. Nelson, A.R., Olson, J.H., Sandler S.I, "Sensitivity of Distillation process Design and Operation to VLE Data", Ind. Eng. Chem. Process Des. Dev., 22, 547-552 (1983). [ Links ]
14. Okasinski, M., Doherty, M., "Thermodynamic behavior of reactive azeotropes", AIChE J., 43, 2227-2238 (1997). [ Links ]
15. Pöpken, T., Götze, L., Gmehling, J., "Reaction kinetics and chemical equilibrium of homogeneously and heterogeneously catalyzed acetic acid esterification with methanol and methyl acetate hydrolysis", Chem. Eng. Chem. Res., 39, 2601-2611 (2000). [ Links ]
16. Prausnitz, J., Lichtenthaler, R., Gomes de Azevedo, E., Molecular thermodynamics of fluid-phase equilibria, 3rd ed , Prentice Hall PTR, New Jersey (1999). [ Links ]
17. Song, W., Venimadhavan, G., Manning, J., Malone, M., Doherty, M., "Measurement of residue curve maps and heterogeneous kinetics in methyl acetate synthesis", Ind. Eng. Chem. Res., 37, 1917-1928 (1998). [ Links ]
18. Streich, M., Kistenmacher, H., "Properties Inaccuracies Influence Low Temperature Designs", Hydrocarbon Process, 59, 237-241 (1979). [ Links ]
19. Sugiyama, K., Saka, K., Kagaku Kogaku, 33, 470 (1969). [ Links ]
20. Ung, S., Doherty, M., "Theory of phase equilibria in multireaction systems", Chem. Engng. Sci., 50, 3201-3216 (1995). [ Links ]
21. Venimadhavan, G., Malone, M., Doherty, M., "A novel distillate policy for batch reactive distillation with application to the production of butyl acetate", Ind. Eng. Chem. Res., 38, 714-722 (1999). [ Links ]
22. Whiting, W.B., Vasquez, V.R., Meerschaert, M.M., "Techniques for Assessing the Effects of Uncertainties in Thermodynamic Models and Data", Fluid Phase Equilibria, 158-160, 627-641 (1999). [ Links ]














