Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.33 n.3 Bahía Blanca jul./sept. 2003
Superheated steam drying of parsley: a fixed bed model for predicting drying performance
M. A. Martinello1, M. A. Mattea1 and G. Crapiste2
1 Facultad de Ingeniería - Universidad Nacional de Río Cuarto
Ruta 36 - Km 601 - 5800 Río Cuarto - Argentina
mmartinello@ing.unrc.edu.ar
2 PLAPIQUI (Universidad Nacional del Sur – CONICET)
La Carrindanga, Km. 7 - C.C. 717 - 8000 Bahía Blanca – Argentina
Abstract ¾ Superheated steam drying technique has been known for a long time, but its application to food drying has received little attention. In this work, superheated steam was applied to dry fresh parsley (Petroselinum Cripsum). A mathematical model to simulate this drying process was developed by using mass and energy conservation equations for solid and steam phases. The resulting partial differential equation system was solved by means of a finite difference method. Software Matlab 5.3 for Windows was used for programming the algorithm. The development of the drying kinetics equation, required in the model, was based on thin layer experimental results. The simulation model was used to analyze the influence of different variables (bed height, operating pressure, steam velocity and steam temperature) on solid moisture content, as well as on solid and steam temperature profiles along the bed. Experimental determinations in a fixed bed arrangement were done at different operating pressures (0.07-0.17 kgf/cm2), steam temperatures (70-100oC), steam velocities (5-12 m/sec.) and bed heights (thin layer, 2 cm and 10 cm). Solid temperature at the top of the bed and average solid moisture content were measured as drying proceeded. An acceptable agreement between experimental and theoretical average solid moisture contents was obtained.
Keywords ¾ Parsley Drying. Superheated Steam. Fixed Bed.
I. INTRODUCTION
The principle of drying with superheated steam has been known for a long time and its industrial utilization increased significantly in the last years. Superheated steam drying presents potential benefits, although it is necessary to analyze the convenience of its application for a particular product. Besides the energy saving and environmental benefits, the oxygen-free atmosphere appears to improve product quality by retarding some deterioration reactions. Under-atmospheric pressures are often required with foodstuffs, which are sensitive to high temperatures due to denaturalization reactions. Several research works have been presented in the literature about the application of superheated steam drying for different solid materials and drier types, but references to drying of foodstuffs are relatively scarce (Akao, 1983; Nomura and Hydo, 1985; Denventer and Heijmans, 2000; Elustondo, 2001).
Solid drying in a packed bed circulated by a gaseous thermal agent is a complex, non-steady state process in which fundamental transfer phenomena appear simultaneously. Different fixed bed models have been developed for air drying, but there are a few references about fixed bed drying using superheated steam (Khan et al., 1991; Wimmersted and Hager, 1996; Elustondo, 2001).
A fundamental information required in dryer modeling is the drying kinetics. Several works related to steam drying kinetics have been reported, most of them for porous inorganic materials (Perre et al., 1993; Shibata and Ide, 1991; Wimmersted et al., 1997; Cenkowski et al., 1996; Daurelle et al. ,1998; Topin et al., 1999; Hager et al., 2000; Elustondo, 2001).
The main objectives of the present work were to obtain an adequate drying kinetics expression for superheated steam drying of parsley from thin layer drying experimental data, and to develop a fixed bed model for superheated steam drying of vegetables that allows to analyze the influence of different process variables.
II. EXPERIMENTAL
Fresh parsley (85-87% w.b. moisture content), bought at a local market, was dehydrated in a pilot plant steam dryer (Elustondo, 2001). The experimental device consists of an insulated drying chamber connected to a vacuum pump. The solid is placed in a perforated bottom basket. The steam is heated by an electrical resistance and conveyed through the solid bed by a fan. The equipment is provided with an automated steam temperature control, a velocity controller connected to the fan motor, a pressure gauge, and a thermocouple for solid temperature measurement.
Experiments were performed under different operating pressures, P (0.07-0.17kgf/cm2), steam temperatures, Tv (70-100oC), steam velocities, v (5-12 m/sec.), and bed heights, L (thin layer, 2 cm and 10 cm). The experimental determinations provided the total weight of the packed bed and solid temperature at the top of the bed, for different times, as drying proceeded. Experiments in a thin layer arrangement were carried out in order to obtain the drying curves (solid moisture content vs. time) for different drying conditions, which were used in the estimation of the kinetic equation parameters.
III. MODELING
A. Drying Kinetics
Drying of foodstuffs involves several transport mechanisms so that drying behavior can be influenced by a large number of variables. The mechanisms involved in the drying process are heat transfer from the external drying medium to the solid surface combined with heat transfer within the material; and mass transfer from the interior of the solid to its surface, followed by external mass transport to the surroundings. One or more mechanisms can control the drying rate, depending on the solid characteristics and the drying agent conditions. No constant drying rate period is observed when drying hygroscopic materials (solids where the water exerts a vapor pressure lower than the saturation pressure) or when the process is internally controlled. In drying with superheated steam, the rate of vapor transport from the solid interface is not limited by mass transfer resistance, and thus the rate of evaporation from the surface is heat transfer controlled (Khan et al., 1991; Wimmerstedt and Hager, 1996).
A single generalized model that includes all pertinent transport mechanism inside the solid and the external heat transfer is proposed (Strumillo and Tadeuz, 1986). The time derivative of solid moisture content in dry basis is given by:
 (1)
(1)
K is the drying rate coefficient that can be represented as follows:
K = k nwc (2)
where k is a relative drying coefficient depending on material parameters, and nwc is the theoretical drying rate in the constant rate period that depends on drying conditions only:
nwc = hv (Tv - Tsat) / l (3)
Here Tv is the steam temperature and Tsat is the saturation temperature at the operation pressure. The heat transfer coefficient, hv, was calculated by using correlations from the literature (Khan et al., 1991):
hv = a(kv / lp)(Cpvmv / kv)l (rvvlp / mv)m (4)
Steam properties were considered constant, except for steam density which was calculated by using the ideal gas law. With these assumptions Eqn. 4 can be written as:
hv = a1 (P v / Tv)m (5)
As an approximation, equilibrium solid moisture contents, Xe, obtained from measurements in humid air can be used for steam drying applications. Water activity, aw, is calculated as the ratio between the operating pressure and the saturation pressure at the steam temperature (Wimmersted and Hager, 1996). In this work, equilibrium isotherm data for parsley (Alcalá et al., 1995) were fitted to the GAB equation to obtain:
 | (6) |
| c1=10.52 k=1.05 m0=3.55 |
By introducing Eqns. (2), (3) and (5) into Eqn. (1), the following expression was obtained:
 (7)
(7)
Model parameters were determined by linear fitting using the experimental data for thin layer, resulting in b=0.046 (kg/kgss min), m=0.4683 and n=0.9051. In this equation v is in [m/sec.] , Tv in [oC] and P in [kgf/cm2].
Drying rate, nw, required in the fixed bed model, is obtained by using Eqn. (7) in the drying rate definition:
 (8)
(8)
B. Fixed Bed Model
The fixed bed model developed in this work is based on plug flow and external heat transfer considerations. The following non-dimensional variables were defined:
Ts*=(Ts-Tven)/DT; Tv*=(Tv-Tven)/ DT;
X*=X/Xin ; G*=G/Gen;
t*= t/tR; z*=z/L
where Ts is the solid temperature, G the steam flux and DT=Tsin –Tven. The subscripts in and en means initial conditions and entrance values respectively.
The governing equations considered in the model are the mass and energy balances for the solid phase (parsley) and the fluid phase (steam):
 | (9) |
 | (10) |
 | (11) |
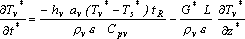 | (12) |
The boundary conditions are:
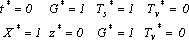 | (13) |
The solution of the proposed model was accomplished by using a finite difference technique. The software used for programming the algorithm was Matlab 5.3 for Windows.
IV. RESULTS
The obtained drying kinetic equation allows the prediction of operative variables influence in solid drying rate. It was found that higher steam temperatures and velocities produce higher drying rates, although they are limited by mechanical and product quality considerations. On the other hand, there is an optimum value of pressure that gives a maximum drying rate (see Fig. 1, Fig.2 and Fig.3).
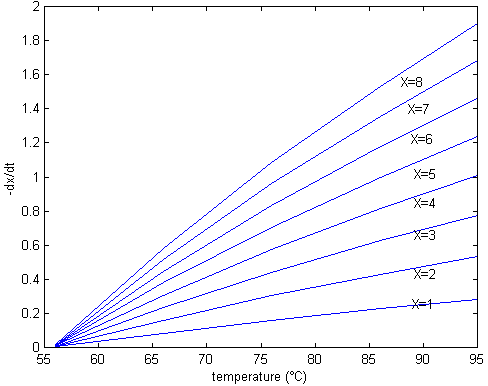
Fig. 1. Influence of steam temperature in drying rate.

Fig. 2. Influence of steam velocity in drying rate.
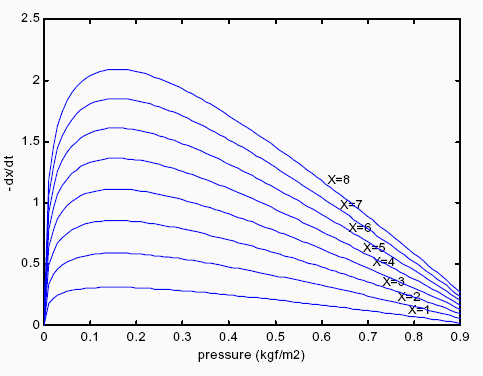
Fig. 3. Influence of pressure in drying rate.
The influence of operative variables, such as pressure, bed height, steam temperature and velocity, in solid moisture content, can be analyzed by using the developed fixed bed model. For instance, the influence of bed height in the average solid moisture content, Xav*, as a function of drying time can be observed in Fig. 4. Experimental results are presented in the same figure.
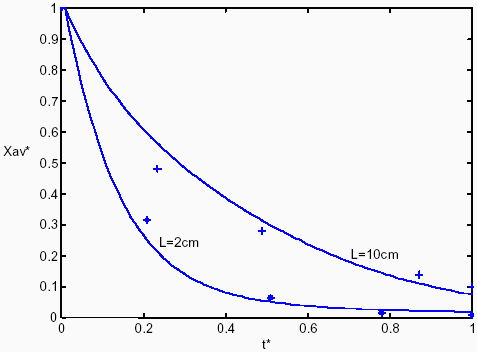
Fig. 4. Bed average solid moisture content. P=0.08 kgf/cm2 , Tven =100oC, v=12 m/sec.
The fixed bed program also allows the calculation of temperatures, moisture content and steam flow profiles along the bed and their variation with drying time (see Fig. 5, Fig. 6, Fig.7 and Fig. 8).
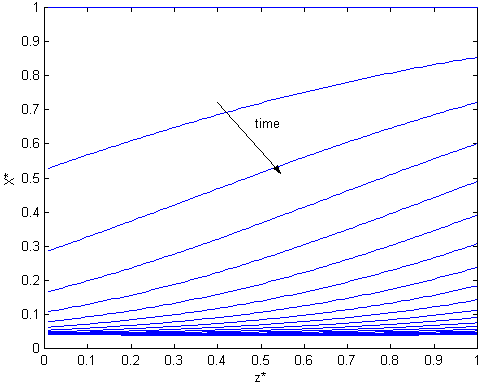
Fig. 5. Solid moisture content profiles along the bed. P=0.08 kgf/cm2 , Tven =100oC, v=12 m/sec, L=2 cm.
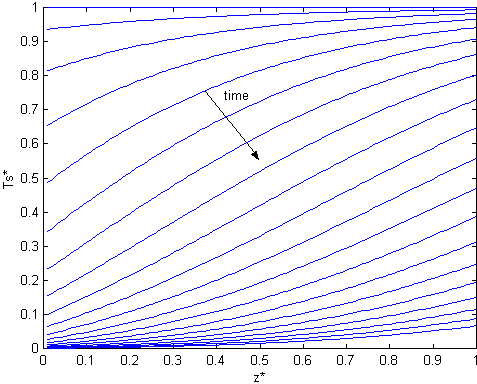
Fig. 6. Solid temperature profiles along the bed. P=0.08 kgf/cm2 , Tven =100oC, v=12 m/sec, L=2 cm.

Fig. 7. Steam temperature profiles along the bed. P=0.08 kgf/cm2 , Tven =100oC, v=12 m/sec, L=2 cm.
Bed height shows a considerable influence in drying rate: as bed height increases drying rate is slower and the required time to get the desired final solid moisture content increases.
This higher residence time can affect product quality. It has been observed experimentally that there is an important bed resistance to steam flow, thus the bed height increment is limited.

Fig. 8. Steam flux profiles along the bed. P=0.08 kgf/cm2 , Tven =100oC, v=12 m/sec, L=2 cm.
V. CONCLUSIONS
A useful tool for steam drying performance prediction has been obtained for an application not much explored, such as vegetable drying under vacuum conditions. Steam drying characteristics of parsley can be analyzed by using the obtained kinetic equation. Simulation results allow getting important conclusions about the influence of different variables in the fixed bed drier performance. Drying rate increases with steam temperature and velocity, decreases with bed height, and has an optimum with operating pressure.
Nomenclature
| av | specific direct heat and mass transfer area, m2/m3 |
| aW | water activity |
| Cp | specific heat, Kcal/kg ºC |
| G | steam Flux, kg/m2 sec |
| hv | film heat transfer coefficient, Kcal/m2 sec ºC |
| L | bed height, m |
| lp | particle dimension |
| Mw | steam molecular weight, kmol/kg |
| P | pressure, kgf/cm2 |
| R | ideal gas constant |
| t | time, sec. |
| T | temperature, oC |
| tR | residence time: L/v, sec. |
| v | steam velocity, m/sec. |
| X | solid moisture content, d.b. |
| z | axial coordinate, m |
Greek symbols
| e | bed porosity |
| l | heat of vaporization, Kcal/kg |
| r | density, kg/m3 |
Subscripts
| av | average |
| v | steam |
| s | solid |
| ss | dry solid |
| e | equilibrium |
| in | initial |
| en | entrance |
REFERENCES
1. Akao, T., Applications of Pressurized Superheated Steam to Food Processing. Chemical Engineering Symposium Series I, The Society of Chemical Engineers Japan 13, 239-268 (1983). [ Links ]
2. Alcalá, M., Gómez, R., Espejo, J., Esteba, M., Marcos, A., Isotermas de Adsorción de Humedad de Algunas Especias Desecadas, Alimentaria Enero 95, 53-59 (1995). [ Links ]
3. Cenkowski, S., Bulley, N. R. and Fontaine, C.M., Dynamics of Drying Bentonite in Superheated Steam and Air as a Model Food System, Can. Agric. Eng. 38 4, 305-310 (1996). [ Links ]
4. Daurelle, J.V., Topin, F. and Occelli, R., Modelling of Coupled Heat and Mass Transfer with Phase Change in a Porous Medium: Application to Superheated Steam Drying, Num. Heat Transfer Part A 33, 39-63 (1998). [ Links ]
5. Deventer, H. C. and Heijmans, R. M. H., Drying with Superheated Steam, Proceeding of the International Drying Symposium 2000. Holland (2000). [ Links ]
6. Elustondo, D. M., Deshidratación de Productos Frutihortícolas con Vapor Sobrecalentado, Doctoral Thesis, PLAPIQUI, Universidad Nacional del Sur, Argentina (2001). [ Links ]
7. Hager, J., Wimmwersted, R. and Whitaker, S., Steam Drying of Porous Spheres: Theory and Experiments, Chem. Eng. Sci. 55, 1675-1698 (2000). [ Links ]
8. Khan, J.A., Beasley, D.E. and Bulent, A., Evaporation from a Packed Bed of Porous Particles into Superheated Vapor, Int. J. Heat Mass Transfer 34 1, 267-280 (1991). [ Links ]
9. Nomura, T. and Hydo, T., Behavior of Inversion Point Temperature and New Applications of Superheated Vapor Drying, Drying85, 517-521 (1985). [ Links ]
10. Perre, P., Moser, M. and Martin, M., Advances in Transport Phenomena during Convective Drying with Superheated Steam and Moist Air, Int. J. Heat Mass Transfer 36 11, 2725-2746 (1993). [ Links ]
11. Shibata, H. and Ide, M., Superheated Steam Drying of Sintered Spheres of Glass Beds under Vacuum, Drying Technol. 9 3, 657-675 (1991). [ Links ]
12. Strumillo, S. and Tadeuz, K., Drying Principles Applications and Design, Gordon and Breach Science Pub., 39-64 (1986). [ Links ]
13. Topin, F., Rahli, O. and Tadrist, L., Experimental and Numerical Analysis of Drying of Particles in Superheated Steam, J. Porous Media 2-3, 205-229 (1999). [ Links ]
14. Wimmerstedt, R. and Hager, J., Steam Drying: Modelling and Applications, Drying Technol. 14 5, 1099-1119 (1996). [ Links ]
15. Wimmerstedt, R., Hager, J. and Hermansson, R., Modelling Steam Drying of a Single Porous Ceramic Sphere: Experiments and Simulations, Chem. Eng.Sci. 52, 1253-1264 (1997). [ Links ]














