Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.33 n.4 Bahía Blanca oct./dic. 2003
On-line estimation of communication time delay in a robotic teleoperation system
C. E. García1, J. F. Postigo2, A. Castro2, R. Carelli2 and B. Kuchen2
1 Departamento de Automática, Ingeniería Electrónica e Informática, Universidad Politécnica de Madrid
José Gutierrez Abascal 2, 28006, Madrid, Spain.
e-mail: {cgarcia@etsii.upm.es}
2 Instituto de Automática, Universidad Nacional de San Juan.
Av. Libertador San Martín (oeste) 1109. J5400ARL. San Juan, Argentina.
e-mail: {cgarcia; jpostigo; acastro; rcarelli; bkuchen}@inaut.unsj.edu.ar.
Abstract ¾ An estimation technique to compute on-line the communication time-delay in a robotic teleoperation system is presented. The proposed algorithm is based on the concept of correlation function and time-delay estimation. The estimation is obtained with an additional signal injected through the communication channel, that is correlated to another signal (of the same kind) generated at the remote station. This way, the correlation function is computed along with its maximum which, multiplied by the sampling time, will result in the desired time delay. Simulation results show the improvement of the teleoperation system performance when using both the communication time delay compensation structure and the time delay estimator. Finally, a comparison between the proposed algorithm and Matlab's xcorr function to compute time delay is performed.
Keywords ¾ Automatic Control. Time Delay Estimation. Compensation Structure. Telerobotic System. Hybrid Position-Force Control.
I. INTRODUCTION
In recent years, several experiments have proved that the execution time needed by a human operator to do a task with a robotic teleoperation system, is significantly dependent on the communication time delay, on the task complexity and on the control structure of the system. In 1965, Ferrel verified that the human operator can adapt his/her motions using a so called "move and wait" strategy so as to prevent destabilising the robot teleoperation system and other associated problems (Ferrel, W. R., 1965). With this control strategy, the operator performs a discrete motion command, then he/she stops and waits (round-trip delay time) for the confirmation that the control action has been followed by the remote robot manipulator or by the remote mobile robot. After this, the operator sends another discrete reference command, and the control cycle repeats itself. The control strategy thus keeps working.
Experimental results in the last two decades, have shown the problems of communication time delays in teleoperation systems (Sheridan, 1993). Hence, much effort has been put on designing control structures capable of compensating communication time delays, though, as for today, no approach can prevent their effects completely. Predictor displays areis an alternative approach to solve some of the problems caused by time delay. Whith this technique, a cursor or other visual pointer is generated by a computer and they are forward time-extrapolated. This helps the human operator predict what will happen in the remote system upon sending a certain reference command from the local station.
If the force is backfed, when time delays are present, the problem is worsened. In 1963, Ferrel proved that it is unacceptable to backfeed continuously the remote sensed force to the same hand with which the operator is manipulating the local hand-controller in a robotic teleoperation system (Ferrel, W. R., 1963). This is due to the time delay in the feedback loop imposing a non-expected perturbation on the human operator´s hand, which he/she cannot ignore, thus provoking instability in the entire teleoperation process. If a visual display were available, the human operator could ignore the perturbation and, in this case, he/she could apply the move and wait strategy or some kind of supervision strategy to avoid system instability.
In previous works (García et al., 2000a; García et. al. 2000b), a time delay compensation approach was presented. This approach was a Smith- Ppredictor based compensation method (Marshall, 1979). Smith- Ppredictor's method calls for a good model of the system part that lacks a time delay, because this part of the model will be part of the control loop.
As mentioned above, the presence of time delay in data transmission between local and remote stations is a particularly important problem to solve in robotic teleoperation, for it can cause instability in the entire system. If this time delay is variable, this problem worsens up because the proposed control structures do not account for time-delay variation. Hence, aiming at obtaining a control structure for broader applications, we have included in the proposed compensation structure an algorithm for estimating the time delay and its subsequent updating.
The paper is organized as follows. Section II briefly reviews the model of the robot teleoperation system. Section III shows in detail the algorithm for on-line time delay estimation. Simulation results are described in Section IV. Finally, Section V summarizses the paper and presents the main conclusions of the work.
II. MODEL OF THE ROBOT TELEOPERATION SYSTEM
In the local station of the robot teleoperation system, the simplified human operator model is regarded as one of the main components. The model considers both the local manipulator and a linearized replica of the remote station. This replica, a part of the proposed compensation structure, is in charge of compensating the communication time-delay between both stations of the teleoperation system.
Sutton (1992), addresses several human operator models for different real-time applications. The model of the human operator used in this work is a linear one, defined by;
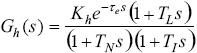 | , (1) |
where Kh is the gain constant of the human operator, te is the reaction time delay of the operator, TL is the operator lead time constant, TN is the neuromuscular lag time constant, whereas TI is the operator lag time constant. The lead and lag time constants are related to the adaptability of the human operator to different dynamical models, according to the task being executed.
The local manipulator's linear model along with its PD local controller is,
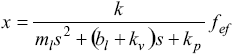 | , (2) |
where k is the gain of the local manipulator–controller closed loop, fef is the total force exerted by the human operator on the local manipulator, kv and kp are PD controller gains; ml and blare the local manipulator's inertia and friction coefficients, respectively, and x is the position of the local manipulator in Cartesian coordinates. The proposed compensation control structure based on the Smith's predictor design can be found in a previous work (García et al., 2000a). The structure is model-based; therefore, the system performance will depend on how precisely the model is known. The replica of the remote station placed at the local station improves the teleoperation system performance, avoiding overshoots in its time response (García et al., 2000a). Figure 1 shows a scheme of the proposed local station for the teleoperation system.
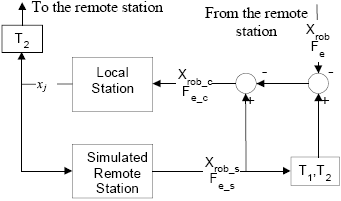
Figure 1: Scheme of the local station.
In Fig. 1, xj is the reference signal sent by the human operator to the remote station, xrob and Fe are the position and interaction force signals being backfed from the remote station to the local station, respectively; xrob_s and Fe_s are the estimates of the signals xrob y Fe respectively; xreb_c y Fe_c are the compensated signals that are sent to the human operator. T1 y T2 are the time delays of the data and visual signals, respectively.
The model of the simulated remote station is linear, since the remote manipulator model (a two-dof-robot manipulator) is assumed to be known, a PD controller plus inverse dynamics and an impedance loop was used for its control.
As previously mentioned for the local station, the remote station is also made up of two parts: the real robotic manipulator and the environment where the task is being carried out. It also includes a local station model that performs as a predictor for reference signals that are commanded from the local station. To make viable the above, it is necessary to pre-program the task.
The dynamical robot manipulator model in Cartesian coordinates is presented in Eq.(3). In this model, the robot is interacting with the environment;
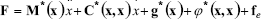 , (3)
, (3)
where 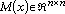 is the inertia manipulator matrix, with
is the inertia manipulator matrix, with 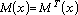 and
and 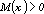 ;
; 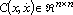 is the centrifugal-and-Coriolis-forces matrix;
is the centrifugal-and-Coriolis-forces matrix; 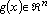 is the vector of gravitational force or torques,
is the vector of gravitational force or torques, 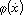 is the friction force,
is the friction force, 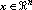 is the vector of Cartesian positions and fe is the interaction force between the manipulator's end-effector and the environment. The control law that was implemented is an impedance robust control, aiming at improving the teleoperation system performance against uncertainties in the dynamic parameters of the robot manipulator. It was described in (Postigo, J. F., et al., 1994), as:
is the vector of Cartesian positions and fe is the interaction force between the manipulator's end-effector and the environment. The control law that was implemented is an impedance robust control, aiming at improving the teleoperation system performance against uncertainties in the dynamic parameters of the robot manipulator. It was described in (Postigo, J. F., et al., 1994), as:
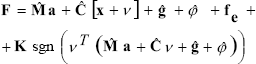 | (4) |
where 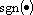 is the sign function and;
is the sign function and;
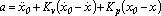 (5)
(5)
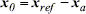 (6)
(6)
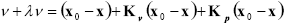 (7)
(7)
Here, 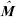 ,
, 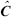 ,
, 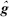 and
and 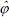 have the same structure as M, C, g and j respectively, though with parameters estimates. Kv and Kp are positive definite gain matrices. K is a diagonal gain matrix. xa is the correction to be done on the position commanded by the human operator, whenever needed in the interaction with the environment. The correction is based on the impedance concept (Hogan, N., 1985). xref is the reference position sent by the operator to the remote robot and x is the robot's actual position.
have the same structure as M, C, g and j respectively, though with parameters estimates. Kv and Kp are positive definite gain matrices. K is a diagonal gain matrix. xa is the correction to be done on the position commanded by the human operator, whenever needed in the interaction with the environment. The correction is based on the impedance concept (Hogan, N., 1985). xref is the reference position sent by the operator to the remote robot and x is the robot's actual position.
The simulated local station is linear and the command estimation given by the simulated operator is,
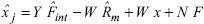 (8)
(8)
with,
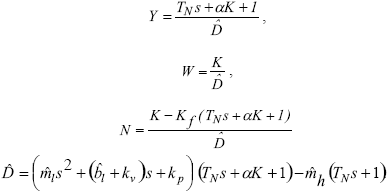 .
.
Finally, the command received by the remote robot is,
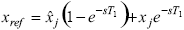 (9)
(9)
Figure 2 shows a block diagram of the remote station implemented for the robot teleoperation system.
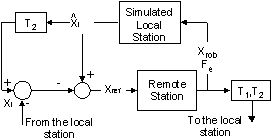
Figure 2: Scheme of the Remote Station.
III. ON-LINE ESTIMATION OF THE COMMUNICATION TIME DELAY
One of the most important problems to face when doing robot teleoperation tasks with position/force feedback is the communication time delay between remote and local stations (and viceversa). This implies a time delay in signal and data transmission between both stations that can cause instability in the teleoperation system. If this time delay is variable, the problem is even worse since most control strategies proposed in the literature, do not take into account for this variation (García et al., 2000a). Simulation results (see Section IV) have shown that the performance of the proposed control structure becomes poor if time delay varies beyond 20% of the considered real value. Since the real time delay of the complete system is 1.9 seconds, a 20% variation about this value would yield a total time delay of 2.28 seconds, that is 0.34 seconds over the nominal value. If dedicated communication channels are being used, this 20% variation may be too much, but for other means, such as Internet, this variaton is insignificant. Therefore, with the objective of proposing a control structure for a broader use, an algorithm to estimate the time delay and its later update was included in the implemented compensation strategy (García et al., 2000a). The algorithm used for on-line estimation of the communication time delay is based on the correlation function concept (Kuchen and Carelli, 1983).
Let us assume that it is necessary to estimate the time delay on the reference commands sent from the local station to the remote station of the teleoperation system. To achieve this, an additional signal (a sine signal, for example) is injected into the communication channel. This signal is correlated with another similar sine signal generated at the remote station and, to obtain this, there must be a synchronization between both signals (Assandri, 2000). It is clear that the sine signal, sent along with the reference commands of the human operator, will be affected by the time delay. Therefore, after correlating both functions and calculating the maximum value of the correlation function, the obtained result is multiplied by the sampling time. This yields the estimate of the communication time delay between the local and the remote stations. Figure 3 depicts a block diagram of the teleoperation system, including the time delay compensation structure and the estimator. It also shows the blocks used to generate the auxiliary signal which estimates the time delay.
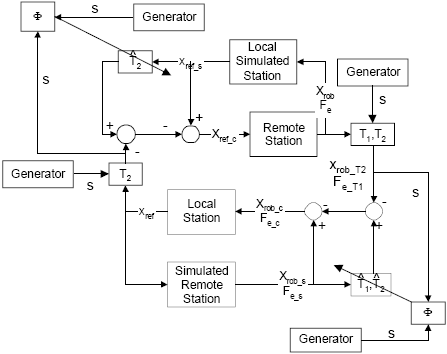
Figure 3: General structure of the teleoperation system.
The estimation of the correlation functions of the random time signals,signals assumes that these signals come from stationary processes, i.e., their statistical properties are not time-variant. Therefore, the classic correlation techniques can only be appliedapplied to time invariant systems (with constant dynamic properties) and where the measured signals come to be stationary ones.
The estimation of the correlation functions is carried out during an experimentation time sufficiently long enough as to obtain consistent statistics properties.
The proposed recursive algorithm (Kuchen and Carelli, 1983) presents some advantages over other classical methods, such as noise immunity and statistic reliability of the obtained results.
The statistic dependence between two time signals x(t) and y(t), which have been discretized in time, can be expressed by its correlation function as,
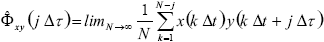 | , (10) |
or,
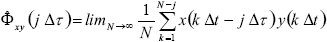 | , (11) |
where:
t = jDt with j = 0,1,.....,M
t = kDt with k = 0,1,.....,N
When needing to compute on-line the correlation function (as it will be discussed later), it is very useful to use Eq. (10), since only future values of y(t) are considered in it. This has no inconveniences when operating off-line and all values of signals x(t) and y(t) are available.
To simplify the notation, let us make Dt = Dt = 1 in Eq. (11), yielding;
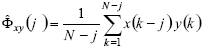 | (12) |
If each new set of measured values tends to improve the estimate, the estimated correlation function will also be a function of the set of measured values until the regarded n time instant. With this, Eq. (12) may be re-written as,
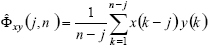 | (13) |
Equation. (13) may be re-written as well, explicitly considering the last pair of measured values as,
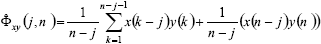 | (14) |
or as,
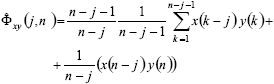 | (15). |
The term 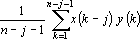 of Eq. (15) represents the estimate of the correlation function in the previous measurement. Considering this, Eq. (15) can be re-written as;
of Eq. (15) represents the estimate of the correlation function in the previous measurement. Considering this, Eq. (15) can be re-written as;
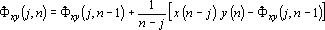 | (16) |
From Eq. (16), it can be noted that the new estimate value 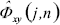 is given by the previous estimate
is given by the previous estimate 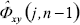 plus a correction term (between brackets) multiplied by the factor factor
plus a correction term (between brackets) multiplied by the factor factor 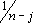 .
.
In Eq. (16), all measured values have the same weight and for values of n greater enough, the influence of the correction factor on the total estimate tends to be smaller each new time. This leads to a smaller influence of the new measured values in the estimation. This last concept is completely justified when working with measured signals in stationary processes, in which, from certain estimate, on, it makes no sense to keep measuring new values, since these new values are less informative.
When the considered systems are non-stationary, and it is needed that the correlation be an updated statistic measure, new measured values should be weighed with higher weights. One method to achieve this,this is to set in Eq. (16) the factor 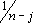 constant, from certain value nl on. This value nl is an indicator of the number of values that are taken into account with higher statistic mean and represents the horizon of values most probably weighed. If now, j = 0, n = nl and k = 1/nl, then Eq. (16) becomes,
constant, from certain value nl on. This value nl is an indicator of the number of values that are taken into account with higher statistic mean and represents the horizon of values most probably weighed. If now, j = 0, n = nl and k = 1/nl, then Eq. (16) becomes,
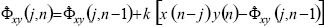 (17)
(17)
Parameter k is also called the forgetting factor.
IV. SIMULATION RESULTS
The recursive algorithm of Eq. (17) was programmed as a MATLAB function, and was included in the robot teleoperation system implemented in Simulink.
This section shows the simulation results using a hybrid position-force control structure (García et al., 2000b), and obtained when the system has an error in the time delay model. A sine signal is injected into the communication channel to carry out the estimation of the time delay. Figures 4 and 5 depict the system performance when considering that the time delay of the teleoperation system has a 20% difference from the real value, in x and y motion axes in space.
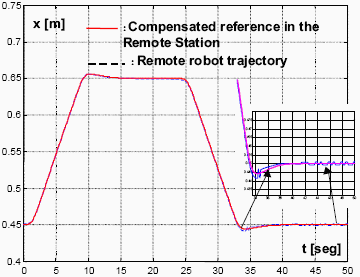
Figure 4: Compensated system performance with a 20% of error on the modeled time delay. Space axis: x.
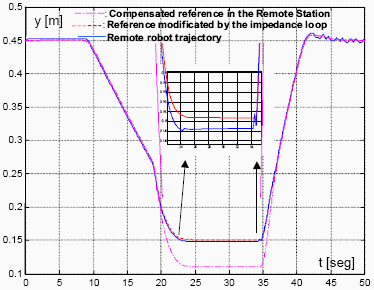
Figure 5: Compensated system performance with a 20% of error on the modeled time delay. Space axis: y.
Figure 6 shows the simulation results considering different values for the forgetting factor k in Eq. (17). In this figure, it should be noticed both the sine signal needed to be estimated and the corresponding estimates carried out by the proposed compensating algorithm. The best result was obtained for a forgetting factor k=170, whereas the worse ones were for k=600 and up. Besides, it was carried out the estimate using the xcorr function of Matlab, with results shown in Figure 7. If the estimates computed with both algorithms are compared, it can be concluded that, when the forgetting factor is increased, the estimate obtained with the proposed algorithm resembles to the estimate given by the xcorr function of Matlab.
Figures 8 and 9 show the estimate error computed by the proposed algorithmproposed algorithm with a forgetting factor k=170 and that obtained with the xcorr function, respectively. It should be noticed that the numerical stability of the xcorr Matlab function is higher than that of the proposed algorithm, though the amplitude of the error signal in this last case is smaller. On account on this last statement, the proposed algorithm seems to be more accurate than the xcorr function of Matlab software.
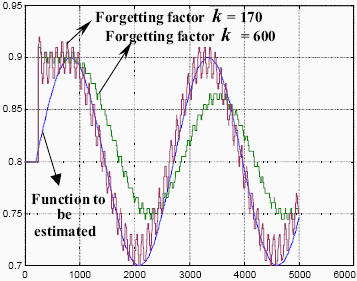
Figure 6: Time delay estimate using different values for the forgetting factor k.
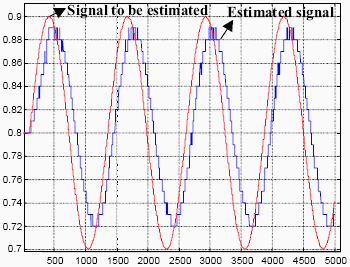
Figure 7: Signal to be estimated and estimated signal using the xcorr function of Matlab.
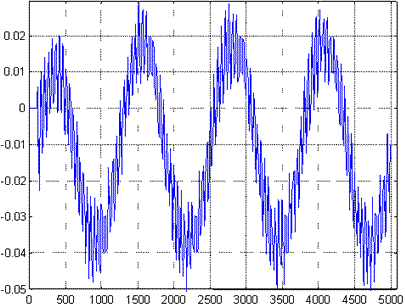
Figure 8: Estimate error with a forgetting factor k = 170.
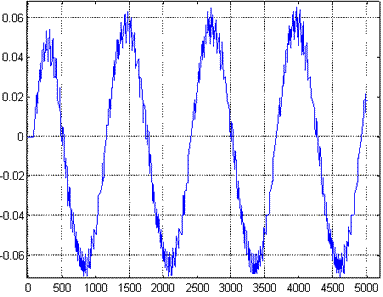
Figure 9: Estimate error using xcorr function of Matlab.
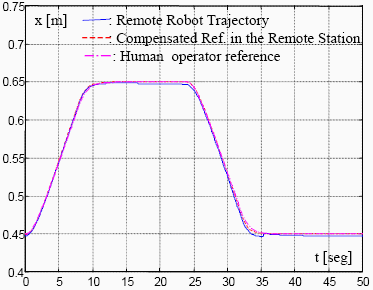
Figure 10: System performance on space axis "x" with a forgetting factor k= 170.
Figures 10 and 11 show the teleoperation system performance when using the algorithm of Eq. (17) to compute on-line the communication time delay. Figures 12 and 13 depict the performance of the teleoperation system when applying the xcorr function of Matlab.
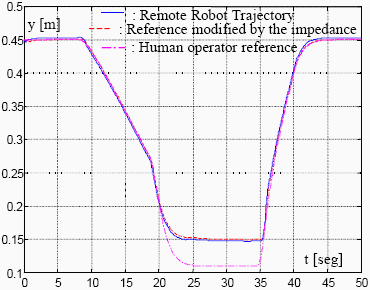
Figura 11: System performance on space axis "y" with a forgetting factor k = 170.
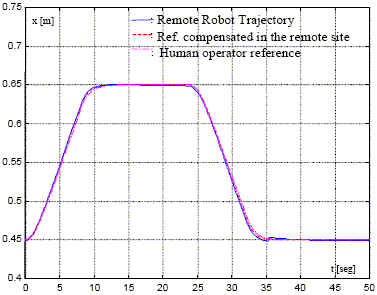
Figure 12: System performance on space axis "x" when using the xcorr function of Matlab.
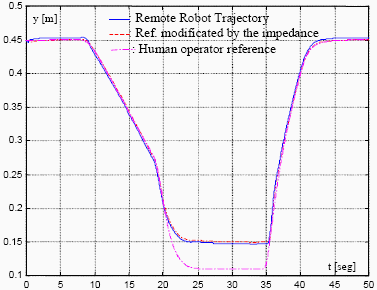
Figure 13: System performance on space axis "y" when applying the xcorr function of Matlab.
V. CONCLUSIONS
An algorithm to estimate on-line the communication time delaytime delays between the local and the remote stations of a robot teleoperation system has been proposed in this paper. This proposed recursive algorithm is based in a compensation structure which uses as the main concept the Smith predictor principle. Simulation curves of Figs. 4 and 5 show the degradation of the system response when the time delay model is not exactly known, thus justifying to include an estimation algorithm in the teleoperation system.
Although the performance of the teleoperation system is acceptable, either when estimating the time delay with the proposed algorithm of Eq. (17) or when using the xcorr function of Matlab, it can be said that the main advantage attained with the proposed algorithm is its computational speed to compute the correlation function. This is so because for each iteration step, an algebraic addition operation is made in order to update the estimation. On the other hand, with xcorr function of Matlab, for each iteration step, the correlation function is computed entirely.
Another advantage of the use of the proposed compensation algorithm is its higher accuracy, although at the expense of a small loss on numerical stability, as noted when comparing Figs. 8 and 9.
Acknowledgments
This work was partially financed by grants both of the Consejo Nacional de Investigaciones Científicas y Técnicas (CONICET), Argentina and the ANPCyT, Argentina.
REFERENCES
1. Assandri A., "Synchronization Protocol of the PC Clock under Windows NT". Master thesis (in Spanish). Universidad de Valladolid, Spain. July 2000 (2000). [ Links ]
2. Ferrel W.R., "Delay Force Feedback". Journal of Human Factors, 449-455. (1963). [ Links ]
3. Ferrel W.R., "Remote manipulative with transmission delay". IEEE Trans. on Human Factor in Electronics HFE, 5, No 1, 145-166 (1965). [ Links ]
4. García C., R. Carelli, J. F. Postigo and B. Morales, "Time Delay Compensation Control Structure for a Robotic Teleoperation System", Proc. of the 4th IFAC International Symposium on Intelligent Components and Instruments for Control Applications - SICICA '2000. Buenos Aires, Argentina, 321-326 (2000a). [ Links ]
5. García C., B. Morales, R. Carelli and J. F. Postigo, "Stability analysis for a teleoperation system with time delay and force feedback", Proc. of the 31st IEEE Conference on Decision and Control (CDC '2000), 1, 3453-3458, Sydney, Australia. December, 12-15 (2000b). [ Links ]
6. Hogan N., "Impedance Control: An approach to manipulation: Part i, Part ii, Part iii". ASME J. Dynamic Syst., Measurement, Control, 107, 1-24 (1985). [ Links ]
7. Kuchen B. and R. Carelli, "Estimación Recursiva de la Función de Correlación". Technical Report, Instituto de Automática, Univ. Nac. de San Juan, Pub. No: RI-T16. (1983). [ Links ]
8. Marshall J.E., "Control of Time Delay Systems", The Institute of Electrical Engineers (IEE), London and New York. Ed. Peter Peregrinus Ltd., Stevenage, UK and New York (1979). [ Links ]
9. Postigo J. F., V. Mut and R. Carelli, "Control Robusto Híbrido de Movimiento-Fuerza para Robots incluyendo Incertidumbre en el Medio". VI Congreso Latinoamericano de Control Automático., 2, 998-1003, Río de Janeiro, Brazil., September, 1994 (1994). [ Links ]
10. Sheridan T. B., "Space Teleoperation Through Time Delay: Review and Prognosis", IEEE Trans. on Robotics and Automation, 9 (5) 592 – 606 (1993). [ Links ]
11. Sutton R., Modelling Human Operators in Control Systems Design, John Wiley & Sons Inc., New York (1990). [ Links ]














