Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.33 n.4 Bahía Blanca oct./dic. 2003
An output feedback algorithm for trajectory tracking in control affine nonlinear systems
V. A. Costa1, R. A. García2 and M. I. Troparevsky2
1 Dto. de Fisicomatemáticas, Facultad de Ingeniería, Univ. Nac. de La Plata, 1900 La Plata, Argentina
vacosta@volta.ing.unlp.edu.ar
2 Dto. de Matemática, Facultad de Ingeniería, U.B.A.
Paseo Colón 850, (1063) Buenos Aires, Argentina
rgarcia@tron.fi.uba.ar, mitropa@tron.fi.uba.ar
Abstract ¾ In this work we present an output feedback algorithm that solves the trajectory tracking problem in control affine nonlinear systems. This algorithm, is an improvement, for this class of systems, of that of (Mancilla Aguilar et al. 2000a), since it reduces the chattering effect on the control while keeping the original performance. In addition, and via a high gain observer, it deals with discrete output measurements instead of the states, as the original algorithm does.
Keywords ¾ Sampled-Data. Chattering. Observer. Output Feedback. Trajectory Tracking.
I. INTRODUCTION
Nowadays, the use of digital computers for the control of continuous-time systems is commonplace. For this reason it is important to study the digital implementation of continuous-time control laws. In this case it is assumed that the states (or outputs) of the system to be controlled are available only at certain times (sampled-data). Since the control is based on these sampled-data, during the intersample periods the control actions applied to the system will be open-loop ones, even if the original continuous-time control law is a feedback one. It is then natural to study the digital implementation of the diverse continuous-time control laws for nonlinear systems, in particular stabilizing or, more generally, trajectory tracking control laws.
Although good results are obtained via the digital implementation via Sample and Zero Order Hold (SZH) of stabilizing laws (see (Mancilla Aguilar et al., 2000b) and the references therein for details), this is not the case for trajectory tracking unless strong assumptions about the tracking control law are made. An example presented in (Mancilla Aguilar et al., 2000a) shows that there is no reason to expect a "nice" behavior of the implementation via SZH of a trajectory tracking control feedback law.
The algorithm proposed in (Mancilla Aguilar et al., 2000a), from now on Algorithm 0, for a rather general class of systems, solves this problem by making the system to follow the trajectories of a model instead of discretizing the continuous-time tracking law. The control law so obtained assures semiglobal practical stability of the tracking error, with final error arbitrarily small for a small enough sampling period. The controller is robust with respect to external disturbances and actuator and data measurements errors, when all of them are small enough.
One of the main drawbacks of Algorithm 0, when applied to control affine systems, appears in the implementation. In fact, as the algorithm is based in a maximization process, when the control space is a polytope, the extremal control values appear at the vertexes. This fact usually gives origin to a chattering effect : the values of the control switch undesirably fast. Another drawback of the algorithm is that it makes use of the states of the system, and in general only discrete-time samples of the output are available.
In this work we develop, for control affine systems, a trajectory tracking algorithm that reduces the chattering effect appearing in Algorithm 0, while it keeps the original tracking error performance. It works with the output sampled-data due to the addition of a high gain observer developed by García et al., (2000), that performs the state estimation.
The paper is organized as follows. In section II we introduce some basic definitions; in section III Algorithm 0 (adapted to control affine systems) is presented and an example where the chattering effect can be observed is shown. In section IV we present a modified algorithm that obtains a high reduction of the chattering effect, while a small tracking error is kept. In section V we review a high gain observer introduced in (García et al. 2000) and present the output feedback algorithm that copes with the two drawbacks mentioned above. In the same section, we apply this algorithm to the example of section III. Finally, the conclusions are presented in section VI.
II. NOTATION AND BASIC DEFINITIONS
Let us start with some basic definitions:  denotes the real interval [0,+¥). The continuous function
denotes the real interval [0,+¥). The continuous function  is of class
is of class  if it is strictly increasing and satisfies g(0) = 0; g is of class
if it is strictly increasing and satisfies g(0) = 0; g is of class  ¥ if it is of class
¥ if it is of class  , is defined in [0, ¥) and
, is defined in [0, ¥) and 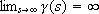 . A continuous function
. A continuous function 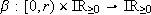 is of class
is of class 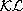 if for each fixed t the mapping b(s, t) is of class
if for each fixed t the mapping b(s, t) is of class  and for each fixed s, b(s, t) is decreasing to zero on t as t ® ¥ (Khalil, 1995).
and for each fixed s, b(s, t) is decreasing to zero on t as t ® ¥ (Khalil, 1995).
we use 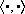 and
and  to denote the Euclidean inner product and the Euclidean norm in
to denote the Euclidean inner product and the Euclidean norm in 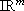 whichever be m, respectively. A function
whichever be m, respectively. A function 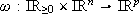 is a feedback control law if for each
is a feedback control law if for each 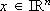 ,
,  is measurable and for each t ³ 0,
is measurable and for each t ³ 0, 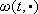 is continuous.
is continuous.
Consider a nonlinear control system described by:
 | (1) |
with 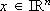 the state,
the state,  the control,
the control, 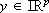 the output,
the output,  ,g = (g1, ..., gm) with
,g = (g1, ..., gm) with 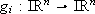 are locally Lipschitz and
are locally Lipschitz and  is the output function. Since we suppose that only the outputs are available, we consider that there exist an estimation
is the output function. Since we suppose that only the outputs are available, we consider that there exist an estimation 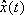 for the state vector x(t), (as might be given by an observer):
for the state vector x(t), (as might be given by an observer):
 (2)
(2)
where the estimation error d(t) satisfies 
We say that 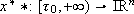 is an admissible trajectory (a reference) for (1) if there exists a bounded measurable function (its generator)
is an admissible trajectory (a reference) for (1) if there exists a bounded measurable function (its generator) 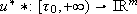 such that x* * (t) is a solution of
such that x* * (t) is a solution of 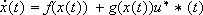 in a compact set of
in a compact set of 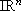 .
.
Definition II..1 Let  be a given reference. We say that a feedback control law w(t, x) solves the closed-loop uniform asymptotic problem (is a CLU for x* ) if the equation of the tracking error e(t) = x(t) - x* * (t)
be a given reference. We say that a feedback control law w(t, x) solves the closed-loop uniform asymptotic problem (is a CLU for x* ) if the equation of the tracking error e(t) = x(t) - x* * (t)

has unique solution for each initial condition and has the origin as an uniformly globally asymptotically stable equilibrium, i. e., there exists b Î 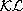 such that
such that  .
.
We will make in the sequel the following assumption, which is instrumental in order to assure the convergence of Algorithm 0 (see Mancilla Aguilar et al., 2000a for details):
H1 w(t, x) is such that there exists a non-decreasing function 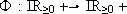 with
with  ;
;
and we will also adopt the following notation:
Given a sampling period d, consider the sampling instants tk = kd, k = 0, 1, ..., and for a positive real number T, let r be the first natural number such that T(d) := rd ³ T; then we denote TN = (d) = NT(d) if  .
.
III. A TRAJECTORY TRACKING ALGORITHM
In this section we present Algorithm 0 adapted to control affine nonlinear systems described by (1).
Let fix a compact set 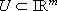 and
and 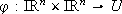 , be a function that verifies:
, be a function that verifies:
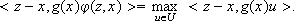 (3)
(3)
Consider the control law defined for each pair 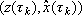 by:
by:
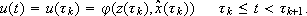 (4)
(4)
Then Algorithm 0 can be described in this case as follows:
- In the interval [TN(d), TN+1(d))] we solve the initial value problem:
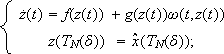 (5)
(5) - For TN(d) £ tk £ t < tk+1 £ TN+1(d), the control u(t) that we apply to the plant (1) is given by (4) with z(t) as in (5), and
 and z(tk) are obtained from (2) and (5) respectively.
and z(tk) are obtained from (2) and (5) respectively.
The next result, that appears in (Mancilla Aguilar et al., 2000a), shows that the final tracking error can be made arbitrarily small for a suitable choice of the sampling period d.
Theorem III..1 Let x* a reference for (1), w(t, x) a CLU for it that verifies H1 and positive real numbers R0 and e0 > 0. Then there exist a compact set 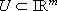 and positive numbers T, d0,
and positive numbers T, d0,  and T' such that if 0 < d £ d and
and T' such that if 0 < d £ d and 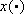 is a trajectory of (1) corresponding to the control
is a trajectory of (1) corresponding to the control  given by Algorithm 0, with
given by Algorithm 0, with  , we have:
, we have:
- there exist a
 -class function D, depending only on b such that
-class function D, depending only on b such that 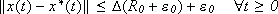
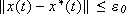 if t ³ T'
if t ³ T'
Although the maximization (3) over a compact set technically sounds, in practice the convex hull of a finite number of points is adopted as the control space, since the evaluation of u(tk) is easier and its value is unique. We consider then,  . In this case Eqn.(3) becomes:
. In this case Eqn.(3) becomes: 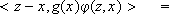

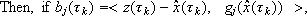 (6)
(6)
the control u given by (4) has now components
 | (7) |
for j = 1, ..., m, and t Î [tk, tk+1).
This control strategy strongly resembles that of the variable structure controllers. In consequence, it is not surprising that a chattering effect may appear, as it is shown in the following simulation.
Consider the control affine system whose state x = (x1, x2) is supposed to be available:
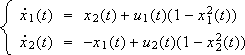 | (8) |
The reference is: 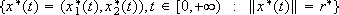 with r* Î (0, 1). The feedback tracking law is: w(t, x) = (w1(t, x), w2(t, x)), with
with r* Î (0, 1). The feedback tracking law is: w(t, x) = (w1(t, x), w2(t, x)), with  and
and 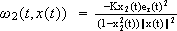 , where
, where 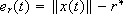 is the radial tracking error. This law verifies the assumption H1 with
is the radial tracking error. This law verifies the assumption H1 with 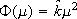 and
and 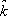 a certain constant.
a certain constant.
Then, er(t) verifies the equation: 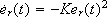 where K is taken such that sign(K) = sign(er(0)), and then the closed loop system will track the reference with an asymptotic decaying error norm given by:
where K is taken such that sign(K) = sign(er(0)), and then the closed loop system will track the reference with an asymptotic decaying error norm given by: 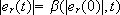 , where b(r, s) = r/(Krs + 1).
, where b(r, s) = r/(Krs + 1).
In the simulations of the application of Algorithm 0 to this example, we adopted the values: T = 2; d = 0.04; u = (u1, u2) Î [-1,1] ´ [-1,1] and K = -7, and the initial conditions (x1(0), x2(0) = (0.2,0). Figures 1 and 2 show the results of the simulations. Figure 2 shows  (the blurred curve) and
(the blurred curve) and 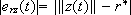 , the modulus of the radial tracking error of the model of the system (the smoother curve) (see Mancilla Aguilar et al., (2000a) for precisions about the model). Figure shows a detail of the tracking controls u = (u1, u2) as given by (7). It can be observed that the controls switch very fast between the values 1 and -1 for any given time interval (the chattering effect).
, the modulus of the radial tracking error of the model of the system (the smoother curve) (see Mancilla Aguilar et al., (2000a) for precisions about the model). Figure shows a detail of the tracking controls u = (u1, u2) as given by (7). It can be observed that the controls switch very fast between the values 1 and -1 for any given time interval (the chattering effect).
IV. THE MODIFIED ALGORITHM
In what follows we introduce a modified algorithm that enables us to overcome the problem of chattering of Algorithm 0. The modifications are made in two steps: in the first one (Step A) a boundary layer is introduced in order to obtain a continuous approximation of the control (7). In the second step (Step B) a prediction strategy is added in order to improve the final tracking error performance of Step A.

Figure 1: Algorithm 0: tracking errors.
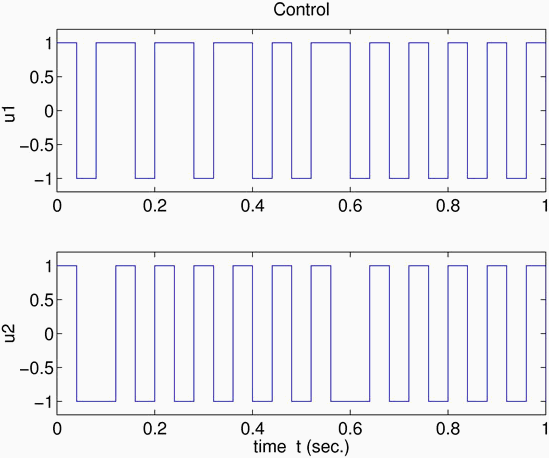
Figure 2: Algorithm 0: controls
 Step A
Step A
As can be easily seen from Eqn.(7), the change of each component uj of the control is consequence of the change of the sign of bj. In order to avoid the fast switching by smoothing out the control discontinuity, we introduce the following modification: given a positive value  , if the value of bj lies in the interval
, if the value of bj lies in the interval 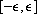 , uj will take its values from a linear interpolation between -aj and aj, and if
, uj will take its values from a linear interpolation between -aj and aj, and if 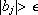 it will take the values given by (7).
it will take the values given by (7).
Then, for a given  and tk < = t < t k+1, the control law u(t) will have now components defined by:
and tk < = t < t k+1, the control law u(t) will have now components defined by:
 | (9) |
j = 1, ..., m, instead of those given by Eqn. (7).
Since Step A consists basically of a smoothing out of the original control discontinuity, it is to be expected that some degradation in the tracking performance with respect to that of Algorithm 0 appears. As a consequence, we introduce in addition a prediction strategy in order to improve the performance.
 Step B
Step B
The (one step ahead) strategy consists in achieving the value of bj in (6) using advanced information give by Eqn. (5) (prediction ). In this scheme, we replace z(tk) by z(tk+1) in (6). The value of z(tk+1) can be obtained from Eqn.(5) as
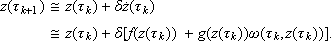 | (10) |
In this way, the value of bj(tk) is obtained as
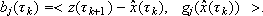 (11)
(11)
Then, for a boundary layer thickness  , the modified algorithm (Algorithm 1) can be described as follows.
, the modified algorithm (Algorithm 1) can be described as follows.
- In the interval [TN(d), TN+1(d)) we solve the initial value problem (5).
- For
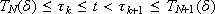 , the control u(t) that we apply to the plant is given by (9), bj given by (11), z(tk+1) as in (10) and where
, the control u(t) that we apply to the plant is given by (9), bj given by (11), z(tk+1) as in (10) and where  and z(tk) are obtained from (2) and (5) respectively.
and z(tk) are obtained from (2) and (5) respectively.
Next, we state a lemma, which is analogous to Lemma 2.1 in (Mancilla Aguilar et al., 2000a), and that can be proved similarly. This lemma shows the behaviour of control u as given by (9)-(11), for the tracking of a reference in a bounded interval of length T.
With this aim, for 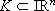 a compact set and a = max{ai, i = 1, ..., m}, let lf and lg the Lipschitz constants with respect to K for f and g respectively, and denote
a compact set and a = max{ai, i = 1, ..., m}, let lf and lg the Lipschitz constants with respect to K for f and g respectively, and denote  ,
,  and l = (lf + alg).
and l = (lf + alg).
For any 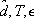 and d positive numbers, let us define
and d positive numbers, let us define 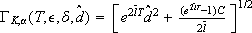 with
with
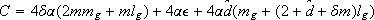 and
and  . The following holds:
. The following holds:
Lemma IV..1 Let 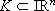 and a as above and pick
and a as above and pick 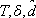 and
and  such that
such that  . Let
. Let 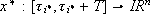 , with ti* = i*d, be a trajectory of (1) such that
, with ti* = i*d, be a trajectory of (1) such that 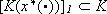 and whose generator
and whose generator 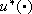 verifies
verifies  . Then if
. Then if 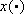 is a trajectory of (1) controlled by u as given by (9)-(11), such that
is a trajectory of (1) controlled by u as given by (9)-(11), such that  , we have:
, we have:
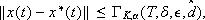 (12)
(12)
 .
.
Remark IV..1 Note that we can make the tracking error arbitrarily small by choosing a suitable d, if  and
and  are small enough.
are small enough.
Remark _IV..2 If we choose the "boundary layer thickness"  too small the chattering effect appears, while if it is too large the final tracking error will also be large. The selection of the optimal value of
too small the chattering effect appears, while if it is too large the final tracking error will also be large. The selection of the optimal value of  follows from an analysis of the magnitude of the control fields
follows from an analysis of the magnitude of the control fields  as x evolves in the compact K.
as x evolves in the compact K.
Remark IV..3 Lemma IV..1 gives a bound of the difference  at each time interval of length T. A bound for the tracking error in the whole tracking time-scale is presented in the next theorem. This result is analogous to Theorem and can be proved in the same way.
at each time interval of length T. A bound for the tracking error in the whole tracking time-scale is presented in the next theorem. This result is analogous to Theorem and can be proved in the same way.
Theorem IV..1 Let x*, w(t, x), R0 and e0 as in Theorem . Then there exist positive numbers a, T, a0,  ,
,  and T' such that if 0 < d £ d0 and
and T' such that if 0 < d £ d0 and 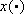 is a trajectory of (1) corresponding to the control
is a trajectory of (1) corresponding to the control  given by Algorithm 1 with
given by Algorithm 1 with  , we have:
, we have:
- there exist a
 -class function D, depending only on b such that
-class function D, depending only on b such that 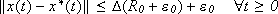
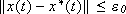 if
if 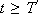 .
.
Remark IV..4 If in addition  is not too small, the resulting control
is not too small, the resulting control  presents no chattering effect.
presents no chattering effect.
V. THE OUTPUT FEEDBACK ALGORITHM
As we stated in the Introduction, generally the values of the states are not available and an estimation of them is needed in order to obtain bj as given by (11). With this aim, in this section we present a high gain observer introduced in (García et al., 2000) for a non-linear continuous time system that is well fitted for this purpose, since it is designed in order to estimate the states when the output measurement is a discrete time process.
According to the assumptions made in (García et al., 2000) we suppose that system (1) verifies the following hypotheses.
- H2: There exist p integer numbers h1, h2, ....., hp that verify:
 , and a globally Lipschitz diffeomorphism
, and a globally Lipschitz diffeomorphism  , with f-1 also globally Lipschitz such that by performing the nonlinear change of coordinates w = f(x), the system (1) can be written as:
, with f-1 also globally Lipschitz such that by performing the nonlinear change of coordinates w = f(x), the system (1) can be written as:
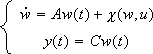 (13)
(13)
where A = diag{A1, ... Ap}, C = diag{C1, ... Cp} where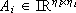 and
and  are in Brunovsky canonical form.
are in Brunovsky canonical form. - H3: There exist two sets of integer numbers {s1, ..., sn} and {q1, ..., qp} with qi > 0
 such that:
such that:  , l = 1, ..., hi - 1; i Î Ip = 1, 2, .. p
, l = 1, ..., hi - 1; i Î Ip = 1, 2, .. p- For c = col{c1, ..., cn},
 1 £ i, j, £ n, j ¹ ml, l Î Ip
1 £ i, j, £ n, j ¹ ml, l Î Ip
- H4 : c is locally Lipschitz with respect to w uniformly with respect to u.
Remark V..1 Hypothesis H3 is sufficient for the local uniform observability of system (1), i.e. that every input be universal for (1) (see García et al., 2000 for details).
A. The observer
The observer presented in (García et al., 2000) is a high-gain one, and the parameter that controls such gain, g, is assumed to have a fixed but arbitrary value. The observer is given by
 For t Î Ik [tk-1, tk) the prediction step is:
For t Î Ik [tk-1, tk) the prediction step is:
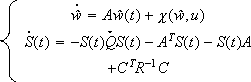 | (14) |
where 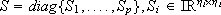 .
.
 The correction step is: in t = tk
The correction step is: in t = tk
 | (15) |
 The initial conditions
The initial conditions 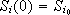 are symmetric positive definite matrices and
are symmetric positive definite matrices and 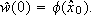
Here 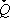 is a fixed positive definite and symmetric matrix, R is diagonal, and both matrices depend on g (see (García et al., 2000) for details). The following result, that was presented in that paper, establishes the convergence of the observer:
is a fixed positive definite and symmetric matrix, R is diagonal, and both matrices depend on g (see (García et al., 2000) for details). The following result, that was presented in that paper, establishes the convergence of the observer:
Theorem V..1 If the conditions H2 - H4 hold, there exists g0 Î (0,1) such that for any g < g0 if the sampling period d is small enough, the system (14)-(15) is an observer for the nonlinear system (1) (for the estimation 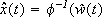 ), that verifies:
), that verifies:
a) when the measures are noiseless, it is an exponential observer.
b) For noisy measurements, the estimation error variance is bounded, and the bound is proportional to the noise variance.
B. The algorithm
The combination of the observer and the Algorithm 1 gives origin to the Output feedback algorithm for trajectory tracking, Algorithm 2, that for a positive number T, a sampling period d and a boundary layer thickness  may be described as follows.
may be described as follows.
- In the interval [TN(d), TN+1(d)) we solve the initial value problem (5).
- For TN(d) £ tk £ t < tk+1 £ TN+1(d), the control u(t) that we apply to the plant and to the observer is given by (9) with bj given by (11) with
 given by (15) and z(tk+1) as in (10).
given by (15) and z(tk+1) as in (10).
The next result, whose proof we omit, assures that for small enough initial estimation error and adequate sampling periods, Algorithm 2 will work properly.
Theorem V..2 Let x*, w(t, x), R0 and e0 as in Theorem , and suppose that system (1) verifies H2 - H4. Then there exist positive numbers a, T, a0,  , ,
, , 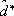 and T' and a number g0 Î(0,1) such that if the observer gain g < g0, the sampling rate 0 < d £ d0 and
and T' and a number g0 Î(0,1) such that if the observer gain g < g0, the sampling rate 0 < d £ d0 and 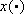 is a trajectory of (1) corresponding to the control
is a trajectory of (1) corresponding to the control  given by Algorithm 2 such that
given by Algorithm 2 such that  , and
, and  , we have:
, we have:
- there exist a
 -class function D, depending on both b and g such that
-class function D, depending on both b and g such that 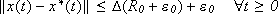
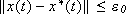 if
if 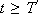 .
.
Remark V..2 If in addition  is not too small the control
is not too small the control  so obtained presents no chattering effect.
so obtained presents no chattering effect.
C. Simulation
In this section we apply Algorithm 2 to the system of the example given in section III. In order to do so we adopt the output function h(x) = x1. Since now the system can be written as:
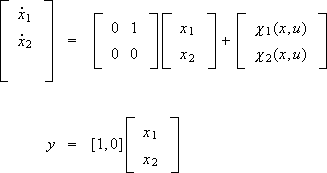
with 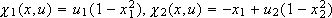 , the hypotheses H2 - H4 are satisfied with {s1, s2} = {1,2}, h1 = 2, m1 = 1 and q1 = 1.
, the hypotheses H2 - H4 are satisfied with {s1, s2} = {1,2}, h1 = 2, m1 = 1 and q1 = 1.
For the simulations we consider a (more realistic) noisy output measurement process with normal distribution given by N(0, 0.01), i. e. y(tk) = x1(tk + vk) with 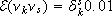 .
.
The design parameters adopted are: 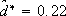 , g = 0.7,
, g = 0.7,  ,
,  where l is the identity matrix, and initial conditions for the observer
where l is the identity matrix, and initial conditions for the observer  . The boundary layer thickness was taken as
. The boundary layer thickness was taken as  = 0.1, and the other parameters were taken as in the simulation in section III.
= 0.1, and the other parameters were taken as in the simulation in section III.
The simulation results are shown in Figs. 3 - 6. In Fig. 3 the estimation errors 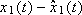 and
and  are shown. In Fig. 4 the tracking errors
are shown. In Fig. 4 the tracking errors  (dotted) and
(dotted) and 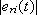 are exhibited, being eri(t) the ideal tracking error of system (8), controlled by the CLU w(t, x). Figure 5 exhibits the tracking controls, as given by Algorithm 2. It can be seen that no chattering effect is present. Figure 6 shows the tracking controls also given by Algorithm 2, but in the case on noiseless measurements. This figure shows that the blurring effect that appears in the controls in Fig. 5 is due to the noise.
are exhibited, being eri(t) the ideal tracking error of system (8), controlled by the CLU w(t, x). Figure 5 exhibits the tracking controls, as given by Algorithm 2. It can be seen that no chattering effect is present. Figure 6 shows the tracking controls also given by Algorithm 2, but in the case on noiseless measurements. This figure shows that the blurring effect that appears in the controls in Fig. 5 is due to the noise.
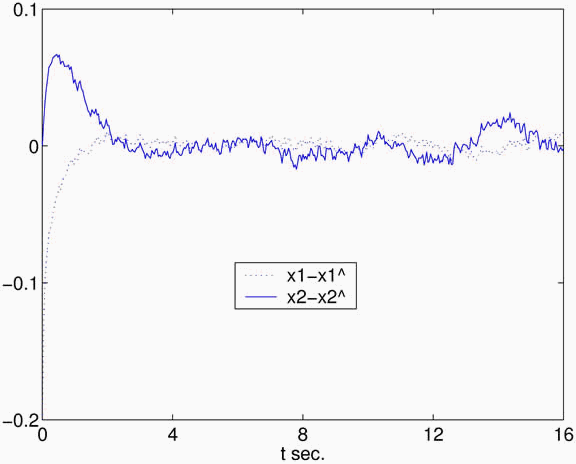
Figure 3: Algorithm 2: estimation errors.

Figure 4: Algorithm 2: tracking errors.

Figure 5: Algorithm 2: controls
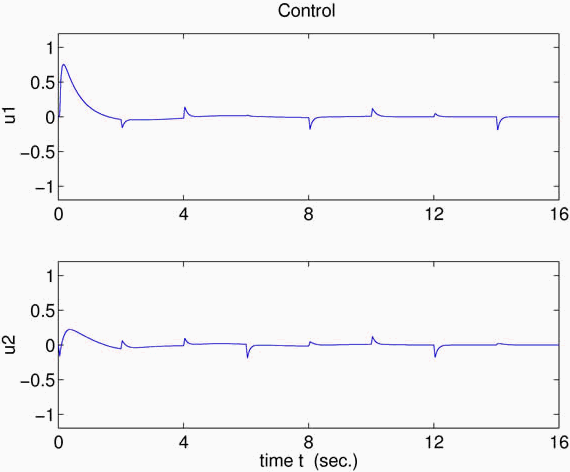
Figure 6: Algorithm 2: noiseless controls
The final tracking error values, as obtained in this simulation and in that of section III, and the behavior of the controls, are presented in the following table. The second column of the table shows  for t ³ 8(sec.) and the third one, the control behavior.
for t ³ 8(sec.) and the third one, the control behavior.

CONCLUSIONS
In this work we presented an algorithm that improves the one of (Mancilla Aguilar et al., 2000a) for the digital implementation of trajectory tracking controllers for control affine systems. This algorithm reduces the chattering effect that appears in the original algorithm while keeping a good tracking error performance. An observer was introduced in order to cope with the case where the states were not available, providing an estimation of the states. It was shown to work properly in a closed loop scheme even with noisy output measurements. Simulations were presented that exhibit the improvements of this strategy for an affine control system.
REFERENCES
1. García R. A. , M.I. Troparevsky and J. L. Mancilla Aguilar, "An Observer for Nonlinear Noisy Systems", Latin American Applied Research 30, 87-92 (2000). [ Links ]
2. Khalil, H., Nonlinear Systems, 2nd Edition, Prentice Hall, New York, (1995). [ Links ]
3. Mancilla Aguilar J.L, R. A. García and M.I. Troparesvsky, "An algorithm for digital implementation of trajectory tracking controllers", Asian Journal of Control 3, 169-179 (2000a). [ Links ]
4. Mancilla Aguilar J.L, R. A. García and M.I. Troparesvsky, "Hybrid Dynamical Systems and Digital Implementation of Feedback Laws", Latin American Applied Research 30, 193-200 (2000b). [ Links ]














