Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.33 n.4 Bahía Blanca oct./dic. 2003
Acoustic emission signal analysis in machining processes using wavelet packets
C. Maradei1, R. Piotrkowski2,4, E. Serrano2, J. E. Ruzzante3,4
1 Instituto de Tecnología "Prof. Jorge A. Sábato", UNSAM-CNEA, Comisión Nacional de Energía Atómica, Avenida General Paz 1499, (1650) San Martín, Buenos Aires, Argentina.
2 Escuela de Ciencia y Tecnología, Universidad Nacional de San Martín, Alem 3901, (1650) San Martín, Buenos Aires, Argentina.
3 Grupo Ondas Elásticas, ENDE, CNEA, Comisión Nacional de Energía Atómica, Avenida General Paz 1499,(1650) San Martín, Buenos Aires, Argentina.
4 Universidad Tecnológica Nacional, Medrano 951, (1179) Buenos Aires, Argentina.
ruzzante@cnea.gov.ar, piotrkow@mail.retina.ar
Abstract ¾ The acoustic emission (AE) phenomenon is useful for monitoring machining processes. AE is directly related to the tool condition, since it is generated by plastic deformation, abrasion, debris fracture, and crack propagation. In the research reported in this paper several AE parameters were measured during the wearing process of a tool insert in turning tests. While some of these parameters are indicative of the wear degree, their applicability in industrial activities is limited. This occurs because the establishment of a control threshold value strongly depends on the process variables. In this paper parameters obtained from the Wavelet Packet (WP) transform coefficients, were employed. They were the Power and the Entropy of the WP coefficients both in the 300 kHz - 600 kHz frequency range. These two parameters were adequate and specific for the determination of the tool condition.
Keywords ¾ Acoustic Emission. Machining. Signal Analysis. Wavelet Packets.
I. INTRODUCTION
The Acoustic Emission (AE) phenomenon is useful for the monitoring of machining processes. The main advantage of AE is that the frequency range of AE signals is much higher than the corresponding to machine vibrations and environmental noise. Moreover, it is non-intrusive in the cut operations. On the other side, AE is directly related to the tool condition, since it is generated by plastic deformation, abrasion, debris fracture and crack propagation.
In their paper, Kannatey-Assibu and Dornfeld (1981) have established that deformation and fracture processes are the main sources of AE in the machining of metals. Three zones can be distinguished in the AE generation:
- Primary deformation zone: the tool cutting edge, while being gradually closer to the material and increasingly pressing it, produces the cutting of the fronting zone. The formed debris moves above the front face of the tool and it is partially deformed.
- Secondary deformation zone: it consists in the debris-tool interface where abrasion and partial deformation take place.
- Tertiary zone: where the abrasion between the new surface generated by the debris detachment and the cutting edge occurs.
The separation and fall-down of the debris, both continuous and discontinuous, and the consequent hitting on the metallic material or the tool, has to be mentioned as an additional AE source (Kannatey-Assibu and Dornfeld, 1981).
Previous theoretical investigations related various cutting parameters with the signal RMS value in the way displayed by Eqn. (1). This relation obtained by Kannatey-Assibu and Dornfeld (1981) considers the primary and secondary AE zones. If we want to apply Eqn. (1), the effects of the tertiary zone have to be minimized. The deviation of the debris to the outside of the working area can minimize the AE generated by debris detachment. The sources corresponding to the tertiary zone can also be diminished by using tools with sharp edges and by considering only the initial stage of the machining process.
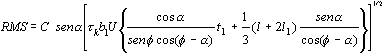 | (1) |
where
b1: cutting width
l1 : length of the sticking zone
l : length of the tool-debris contact zone
U : cutting velocity
t1 : velocity of supply
a: rake angle
j: shear angle
tk: shear stress
C: constant
Equation (1), is a poor approximation to real experiments, but it shows the influence of geometry and velocity on the cutting process. As long as the wear proceeds the geometry of the sample changes and concurrently the variables and constants in Eqn. (1) take different values. Moreover, in simple turning operations, an important degree of AE is generated in the tertiary zone. Because of this a statistical study of the several parameters of the AE signal is required. The trend in nowadays work is to look for statistical parameters related to the tool condition.
One of the common techniques in spectral analysis of signals is the Fast Fourier Transform (FFT), which allows determining the frequency range that is predominant in a continuous signal. A continuous AE signal means that the time interval between emissions with similar amplitude is shorter than or equal to the emission duration So, the starting and ending points of events are not well defined. When discontinuous signals are analyzed with the FFT, a local analysis is performed but when the temporal window is selected, an arbitrary and not always adequate frequency range is simultaneously defined. This is the reason why other transforms such as the Short Time Fourier Transform (STFT) and the Wavelet Transform were created. In the STFT the selection of the width of the temporal window is a non-trivial problem, in particular in cases where short and long time phenomena coexist. This is the case of our signals. Because AE is typically a non-stationary process the Wavelet Transform is a useful tool to manage the data. It can be considered as local Fourier Transform at all different scales.
With the development of the Wavelet theory in the late 80's and the beginning of the 90's, Wu and Du (1996) introduced the Wavelet Packet (WP) transform in the processing of signals coming form vibrations during the machining process. The coefficients obtained with this transformation were then used as parameters for determining the tool condition. Other authors have performed similar successful analysis taking the AE signals, (Xiaoli and Shejun, 1998; Niu et al., 1998; Kamarthi et al., 2000).
The aim of the present paper is to advance in the signal processing and to improve the corresponding extraction of parameters with the WP technique in the cylindrical turning process, in order to determine the tool condition. The analysis consists in various stages. First, average values of parameters directly obtained with the AE system are obtained. Then, digitized signals are analyzed with WP. The analysis is done on continuous signals, which are those connected with the wear degree, after having filtered out the discontinuous ones. This work continues a Master Thesis that took place in the Technology Institute "Prof. Jorge A. Sábato", CNEA, Argentina (Maradei, 2001) and also follows previous work performed in the Elastic Waves Group, CNEA, Argentina, Masetro et al. (1998), Pérez Gallego (1999).
II. EXPERIMENTAL EQUIPMENT
A. Materials
We used bars of two different materials: SAE 1010 and SAE 12L14 steels. The grain size in SAE 1010 steel was heterogeneous, with large grains between 7 and 8 (32 m m and 22 m m) and small grains between 9 and 10 (16 m m and 10 m m), ASTM E112 Standard. Inclusions had variable Al, Si, Mn, S, Ca and Fe content, and a mean size of 2 m m. The hardness profile along the inclusion diameter had a mean value of 86 HRB in the mean, with a deviation lower than 5%. The grain size in SAE 12L14 steel was 8 (22 m m), ASTM E112 Standard. The inclusions and precipitates contained S, Pb, Mn, Fe, and their size was about 3 m m. The hardness profile along the diameter direction had a mean value of 87 HRB with a deviation lower than 5%. This is a rephosphated and resulfured steel with the addition of Pb, so the inclusion content is increased. The presence of brittle inclusions augments the material workability.
B. Acoustic Emission System
The system was MISTRAS 2001 from Physical Acoustics Corporation (PAC). The AE waves were converted to electrical signals by the piezoelectric sensors, then they were preamplified (40 dB) and measured by the AEDSP-32/16B card with channels for signal processing and wave shape determination. Only one of the channels was used, with a sensor located with a coupling wax on the backside of the insert holder, (Fig. 1). A 20 kHz - 1200 kHz passband filter was applied, and then the signal was digitized to 4 Megasamples per second and a resolution of 16 bits. The maximum system capability for hit processing and extraction of parameters was higher than 20000 hits/s.
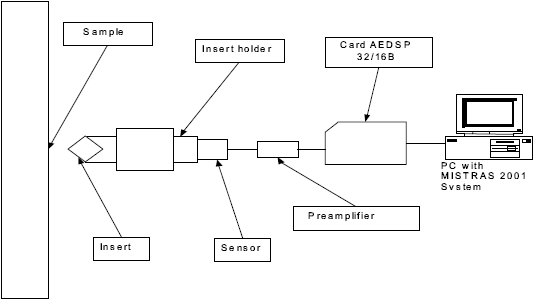
Fig. 1. Experimental Setup.
C. Experimental Procedure
Bars were turned with a 20kW Turri 250 lathe, which had a P20 metallic carbide insert. At the end of the turning of each bar the insert wear degree was measured with a Leitz Wetzlar microscope with micrometric screws according to the ISO 3685 Standard. The parameter values are given in Table 1.
Table 1: Test Parameters
A portion of 15 steel 1010 samples, 335 mm long, were turned in 6 turning steps with the first insert (Test 1) and in 2 turning steps with the second insert (Test 2). A portion of 15 steel 12L14 samples 325mm long was turned in two turning steps (Test 3). When each portion of samples was finished, de diameter was demitted and this led to diminish the ongoing cutting velocity since our lathe was not equipped with a velocity controller. This led to an error of 4% in the velocity, with respect to the considered mean value.
The signals of each turning step of each sample were kept in a different file. Samples "a" corresponded to steel 1010 and samples "b" to steel 12L14. Samples were numbered in a sequential order according to test. The letter "p" indicated the order number of the turning step. For steel 1010 the files had, in the mean 160 events corresponding to low and medium wear degree and 540 corresponding to severe wear. For steel 12L14 the mean number of events per file was 3100. These files preserved also the information on the parameters analyzed in each event.
Being steel 1010 of low machining abilities, for this case a low passing depth was selected. This produced wear in the insert tip, so the standard limit wear could not be considered. In order to overcome this difficulty the maximum length of wear near the tip was considered as a limit value.
III. SIGNAL ANALYSIS WITH WAVELET PACKETS
The signal analysis method implemented in this work is based on the Wavelet Packet Transform.
This is a generalization of the standard Wavelet Transform and allows controlling the analysis precision in the frequency domain (Meyer, 1993). Associated with its implementation there is a wide collection of Orthogonal Bases in the space of signals with finite energy. The selection of the best basis, following an adequate criterion, is just the fact that makes possible the optimal signal representation (Meyer, 1993, Mallat, 1988, Serrano and Fabio, 1996). The elementary functions that constitute the bases, are the wave packets. They can be considered as wavelets with well-defined duration and oscillation pattern, and they extend the collection of standard wavelets, combining in a wide range the time frequency precision.
The Wavelet Packets proposed in (Meyer, 1993) result from the successive application of the pair of conjugated filters associated with the Multiresolution Analysis scheme.
Given a signal, it is possible to perform the analysis through the recursive action of the conjugated filters, in what is named Mallat's Generalized Algorithm (Mallat, 1988). This procedure goes on generating the coefficients that represent the signal in the classes of elementary functions, which are organized in a library of orthonormal bases. When this process is finished, we must select the coefficients that correspond to the optimal basis. This can be done by defining a cut in the tree of alternatives.
Finally we have a representation of the signal as:
 | (2) |
where j J(t) is the wave packet in the optimal basis and cJ is the corresponding representation coefficient.
Since the basis is orthonormal, the signal energy is given by:
 | (3) |
The Information provided by the cJ coefficients depends on the selection criterion adopted for the basis. In particular, if we use the Minimum Entropy Criterion, we are selecting the basis that minimizes the number of significant coefficients in the signal representation.
The entropy S is a parameter that has the meaning of the degree of intrinsic disorder or lack of organization of the signal with respect to a given basis: a relatively low entropy value evidences the existence of a structure recognizable in the elementary patterns. Contrarily, a high entropy value indicates the lack of a simple and identifiable structure (Meyer, 1993, Mallat, 1988, Serrano and Fabio, 1996).
The application of these criteria turns to be very useful, in particular to analyze sequences of signals coming from processes with properties that seem to be stationary in short time intervals but are non stationary. This is the case in the process investigated in the present paper.
IV. RESULTS AND DISCUSSION
At the end of the last passing in Test 1, the insert resulted severely worn out. This did not happen in Test 2, where the maximum value proposed by the Standard was not reached. (VBB= 0.3mm). In Test 3, a wear VBB= 0.3 mm, higher than the standard critical value was reached.
In this paper only the continuous type signals, as named in literature, were analyzed, since they are those that contain information about the wear of the tool. They provide information on the tool and debris fracture. The method that allows the separation of the continuous waves from the discontinuous ones is the stationarity control, following a proposal by Niu et al., (1998). The stationary signals are those which have a mean value (E(Xt)) and an autocorrelation (Rx(t,t+t )) that do not depend on time, so long as the non-stationary are modulated in frequency and magnitude. A signal is stationary if:
 (4)
(4)
that is, from a practical point of view:
 (5)
(5)
being m k and Rx(t ) constants. In Eqn. (4), a tolerance of stationarity control is applied. In this sense, the "stationary" or "discontinuous" sections in signals can be cut apart. This was done in this paper and from now on we consider only the continuous part of signals.
A. Evolution of AE Parameters
An initial data processing consisted in taking the AE parameters extracted by the AE system and perform the average of them in each passing. The energy evolution from Test 1 is shown Fig. 2. We can observe a peak in the middle time of the test. This peak acts as a predictor of changes of the other parameters such as rise-time, count number, amplitude, events per second and duration. After that peak, these five parameters present a descent of their values. Figure 3 shows the energy evolution obtained in Test 2. The energy peak was obtained in the second half part of the test, since in this case the insert did not overtake the standard limit value. After the peak, the rise-time, counts, and amplitude values show an incipient descent while the events per second and the duration suffer an instability in their values that could announce an imminent descent. The energy evolution in Test 3 (Fig. 4) has a similar behavior.
Figures 2 - 4 show that the range of the parameter values and then the threshold that determines the tool condition change with the working conditions. This constitutes a drawback for the adoption of these parameters for diagnosis in industrial applications.

Fig. 2. Energy Evolution in Test 1.
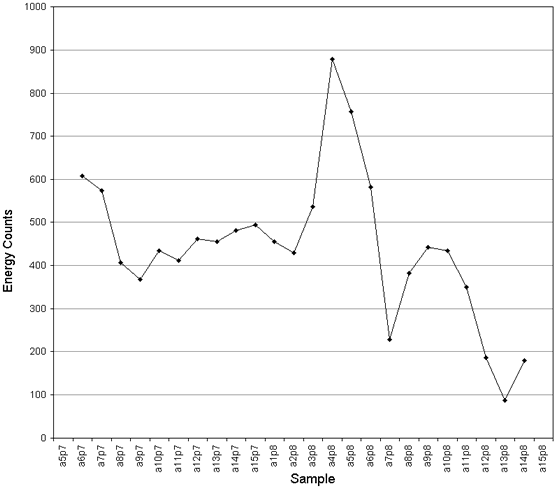
Fig. 3. Energy Evolution in Test 2.
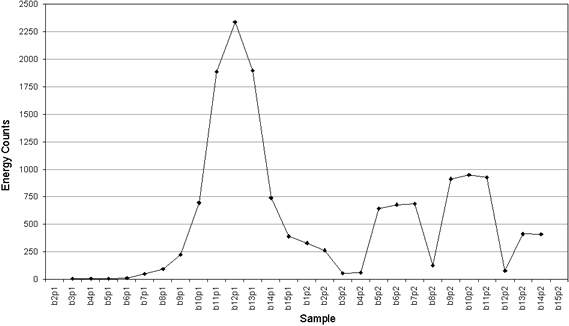
Fig. 4. Energy Evolution in Test 3.
B. Frequency Histogram
Figures 5 and 6 show that while wear advances a predominance of peaks of low frequencies occurs compared with the initial wear stages. Other authors (Heiple et al., 1994) previously observed this shift phenomenon.

Fig. 5. Frequency Histogram for Test 1

Fig.6. Frequency Histogram for Test 3
C. Analysis with Wavelets Packets
The behavior of the parameter energy and the frequency histogram suggest the necessity of treating these signals with methods developed for non stationary processes, such as WP described in section III. In this way we are seeking indicators related to energy.
In previous work of our group (Piotrkowski et al., 1999; Pérez Gallego et al., 2000) Wavelets have been used for signal processing. In the present paper we use WP since each packet gives signal information in a specific time-frequency window. The WP transform was applied to signals and the power was calculated with the WP coefficients as is stated by Eqn. (6). The calculation was performed in the 300 kHz - 600 kHz frequency range, which is rich in information on tool wear.
 | (6) |
The cj s are the WP coefficients in the mentioned range and N is the number of coefficients involved. We used the Haar mother wavelet up to a resolution level of 7. After decomposing the signal the best basis was investigated, in the sense of representing the signal in the most compact way. Specifically we looked for the basis that minimized the entropy of the WP transform coefficients. Shannon-Weaver Eqn. (7) was used for the entropy calculation.
 | (7) |
where pi is (7)
 (8)
(8)
Figures 7-9 show the power (Eqn. (6)) evolution in semi-logarithmic graphs. It can be observed that the graphs resemble those of the parameter energy (Figs. 2-4). The difference is that they are greatly amplified. Another important point is that the power calculation is performed with a fixed time window and does not depend on the total event duration as in the energy case.
It is convenient to calculate other indicators that reinforce or complement the tendency shown by the power indicator, because it has a statistical nature. The frequency shift mentioned above and displayed in Figs. 5-6 suggests an indicator connected with the frequency distribution. Among them the entropy of the coefficients of the WP transform in the 300 - 600 kHz was selected. At values close to 1, the frequency distribution is more uniform in the spectrum and in this respect the phenomenon is more disordered; contrarily, at values close to 0 certain groping or order is found in the frequency distribution. For the entropy calculation the Eqn. (7) was used.
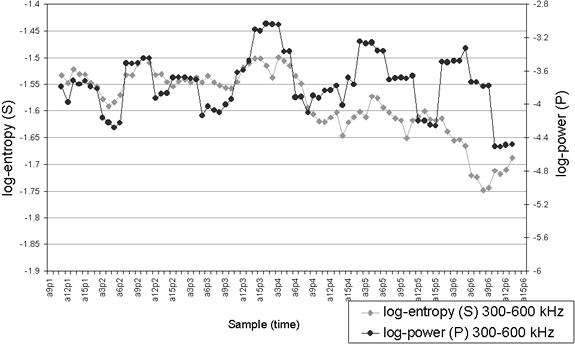
Fig.7. Evolution of log-power (P) and log-entropy (S) calculated with WP in Test 1.

Fig.8. Evolution of log-power (P) and log-entropy (S) calculated with WP in Test 2.

Fig.9. Evolution of log-power (P) and log-entropy (S) calculated with WP in Test 3.
As can be seen in Figs. 7, 8 and 9 the entropy of the WP coefficients in the 300 kHz - 600 kHz frequency band follows the same tendency of power mainly in the middle and final stages. That is to say that there is a peak in the middle wear stage for both parameters and then both decline.
Moreover, entropy has not been used as an independent parameter in literature involved in WP, (Xiaoli and Shejun, 1998; Niu et al., 1998; Kamarthi et al. 2000), but only to obtain optimal trees.
IV. CONCLUSIONS
The AE parameter Energy is indicative of the insert wear. When a maximum peak is produced at an intermediate wear degree a change is obtained in the behavior of other parameters such as Risetime, Counts, Duration and Amplitude. These parameters can be used combined with Energy. The drawback is that all these parameters are sensitive to the turning operating conditions.
Power calculated with the coefficients of the Wavelet Packet Transform in the 300 kHz - 600 kHz frequency range is an adequate indicator of the tool condition. Its evolution with wear degree shows similar morphology for the three tests, but the maximum and minimum values differ for different tests. This parameter could be a useful indicator and act as entry in mathematical tools such as neural networks or algorithms using diffuse logic.
We studied in greater detail with respect to work published by other authors, the instabilities that occur in the middle wear stages in all the AE parameters reported in this paper: Energy, Count Number, Amplitude, Risetime and Duration, obtained from the AE system, and Power and Entropy calculated with WP.
The Entropy of the Wavelet Packet transform coefficients in the 300 kHz - 600 kHz frequency range was used as an independent parameter in this work. It reinforces as an indicator the result obtained with the WP Power in the same range. However, the variation is clearer and more pronounced for the Power parameter.
References
1. Heiple C.R., S.H. Carpenter, D.L. Armentrout and A. Mc Manigle, "Origin of Acoustic Emission produced during single point machining", Materials Evaluation, 52, 590-596, (1994). [ Links ]
2. Kamarthi S.V., S.R.T. Kumara, and P.H. Cohen, "Flank wear estimation in turning through wavelet representation of Acoustic Emission signals", Journal of Manufacturing Science and Engineering, 122, 12-19, (2000). [ Links ]
3. Kannatey-Asibu Jr. E. and D.A. Dornfeld, "Quantitative Relationships for Acoustic Emission from Orthogonal Metal Cutting", Journal of Engineering for Industry, 103, 330-340, (1981). [ Links ]
4. Mallat S., Multiresolution Representation and Wavelets, Grasp. Lap 153, University of Pennsylvania, Philadelphia, (1988). [ Links ]
5. Maradei C., "Estudio de la condición de la herramienta durante el maquinado de piezas mediante emisión acústica", Master Thesis, Instituto de Tecnología "Prof. Jorge A. Sábato" , UNSAM-CNEA., (2001). [ Links ]
6. Masetro J.O. and J.E. Ruzzante, "Monitoreo del desgaste de una herramienta utilizando la técnica de emisión acústica", Technical Report, Instituto Balseiro, CNEA-UNC-UBA, (1998). [ Links ]
7. Meyer Y., Wavelets: Algorithms and Applications, SIAM, Philadelphia, (1993). [ Links ]
8. Niu Y.M., Y.S. Wong, G.S. Hong and T.I. Liu, "Multicategory classification of tool conditions using wavelet packets and ART2 network", Journal of Manufacturing Science and Engineering, 120, 807-816, (1998). [ Links ]
9. Pérez Gallego T., "Aplicación de emisión acústica (EA) a la monitorización de procesos de corte", Technical Report, Universidad de Valladolid, ETSII, (1999). [ Links ]
10. Pérez Gallego T., J. Masetro, E. Serrano, R. Piotrkowski and J.E. Ruzzante, "Characteristic parameters from acoustic emission signals in wear of cutting tools", 15th World Conference on Non-Destructive Testing, Rome, Italy, October 15-21, (2000). [ Links ]
11. Piotrkowski R., G.A. Hirchoren, M.P. Gómez, C.E.DAttellis and J.E. Ruzzante, "Acoustic emission signals from a coating breakdown, 1/f processes and wavelet analysis", Primer Encuentro del Grupo Latinoamericano de Emisión Acústica, Buenos Aires, Argentina, September 6-10, (1999). [ Links ]
12. Serrano E. and M. Fabio, "Application of the Wavelet Transform to Acoustic Signal Processing", IEEE Trans. Acoust. Speech and Signal Processing, 44, 1270-1275, N. 5, (1996). [ Links ]
13. Wu Y. and R. Du, "Feature extraction and assesment using wavelet packets for monitoring of machining processes", Mechanical Systems and Signal Processing, 10, 29-53, (1996). [ Links ]
14. Xiaoli L., Y. Zhejun, "Tool wear monitoring with wavelet packet transform-fuzzy clustering method", Wear, 219, 145-154, (1998). [ Links ]














