Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Latin American applied research
Print version ISSN 0327-0793
Lat. Am. appl. res. vol.33 no.4 Bahía Blanca Oct./Dec. 2003
On the existence of norm-estimators for switched systems
R. A. García1 and J. L. Mancilla Aguilar2
Depto. de Matemática, Fac. de Ingeniería, Universidad de Buenos Aires.
Paseo Colón 850, (1063) Buenos Aires, Argentina.
1 rgarcia@fi.uba.ar
2 jmancil@fi.uba.ar
Abstract ¾ In this paper, we prove the existence of norm-estimators for switched nonlinear systems. The proof is based on an existing converse Lyapunov theorem for IOSS nonlinear systems, and on the association of the switched system with a nonlinear system with inputs and disturbances that take values in a compact set.
Keywords ¾ Norm Estimators. Converse Lyapunov Theorems. IOSS. Nonlinear Switched Systems.
I. INTRODUCTION
Recently, the study of switched systems has received a great deal of attention, being the rapidly developing area of intelligent control an important source of motivation for this study. Informally, a switched system is a family of continuous-time dynamical subsystems and a rule that determines the switching between them. The recent paper (Liberzon and Morse, 1999) is a very interesting survey on the subject, where an updated account of results and open problems may be found.
This paper concerns itself with the following question, for a switched system: is it possible to estimate, based on external information provided by past input and output signals, the magnitude of the internal state x(t) at time t?
State estimation is central to control theory as it arises in signal processing applications (Kalman filters), in stabilization based on partial information (observers), etc. An open question is the derivation of useful necessary and sufficient conditions for the existence of observers, i. e., dynamical systems which provide an estimate  which converges to the state x(t) of the system of interest, using the information provided by the sets of past inputs and outputs, {u(t), t £ t} and {y(t), t £ t} respectively. In order to stabilize a system to an equilibrium (that we will assume with no loss of generality to be the origin) of an Euclidean space, it may suffice to have a norm-estimate, that is to say, an upper bound
which converges to the state x(t) of the system of interest, using the information provided by the sets of past inputs and outputs, {u(t), t £ t} and {y(t), t £ t} respectively. In order to stabilize a system to an equilibrium (that we will assume with no loss of generality to be the origin) of an Euclidean space, it may suffice to have a norm-estimate, that is to say, an upper bound  on the magnitude (norm)
on the magnitude (norm)  of the state x(t). Indeed, it is often the case (Jiang and Praly, 1992; Praly and Wang, 1996) that norm-estimates suffice for control applications. To be more precise, in the context of switched systems, one wishes that
of the state x(t). Indeed, it is often the case (Jiang and Praly, 1992; Praly and Wang, 1996) that norm-estimates suffice for control applications. To be more precise, in the context of switched systems, one wishes that  becomes an upper bound of
becomes an upper bound of  as t ® ¥ uniformly with respect to the switching signal (see next section for precise definitions). We are thus interested in uniform norm-estimators which, when driven by the input-output data generated by a switched system, produce such an upper bound
as t ® ¥ uniformly with respect to the switching signal (see next section for precise definitions). We are thus interested in uniform norm-estimators which, when driven by the input-output data generated by a switched system, produce such an upper bound  irrespectively of the switching signal.
irrespectively of the switching signal.
One obvious necessary property for the possibility of norm-estimation is that the origin must be uniformly (with respect to the switching signal) globally asymptotically stable with respect to the "subsystem" consisting of those states for which the input u = 0 produces the output y = 0. In this case the switched system is uniformly zero-detectable. However this property is not sufficient, since one should ask that, irrespectively of the switching signal, when inputs and outputs are small, states should also be small, and if inputs and outputs converge to zero as t ® ¥, states do too.
On the other hand, the notion of input-output-to-state stability (IOSS), introduced by Sontag and Wang (1997) for a system
 | (1) |
resulted in an useful paradigm in the study of nonlinear detectability. In that paper the authors describe relationships between the existence of full state observers and the IOSS property.
In a recent paper Krichman et al. (2001) proved that system (1) is IOSS if and only if it admits a norm estimator (in a sense that will be made precise in Section 4). This result suggests that, for our purposes, the right notion of detectability is the generalization of the IOSS property to switched systems.
Since in (Krichman et al., 2001) it was also shown that this result is, in turn, a consequence of a necessary and sufficient characterization of the IOSS property in terms of a smooth dissipation function (an uniform IOSS Lyapunov function), the problem that naturally appears in our context may be stated as follows: given a switched system with outputs whose component subsystems are each IOSS, find necessary and sufficient conditions for the IOSS of the switched system, uniformly with respect to the switching signals.
It can be easily shown that the sufficient conditions for IOSS of system (1) established by Krichman et al. (2001) carry over with little changes to the switched system. In fact, the existence of a common IOSS Lyapunov function implies that the switched system is IOSS for arbitrary switching, and that a norm-estimator for this system exists.
The question of the validity of the converse, that arises naturally as a byproduct of the question of the existence of the norm-estimator, originates the problem of the existence of such Lyapunov function, i.e., of the existence of a converse Lyapunov theorem.
In this paper we obtain a converse Lyapunov theorem for a certain class of switched nonlinear systems. This theorem is in the spirit of the converse ones for asymptotic stability, input-to-state stability (ISS) and integral input-to-state stability (iISS) of switched nonlinear systems obtained in (Mancilla Aguilar and García, 2000) and (Mancilla Aguilar and García, 2001) respectively, since we also suppose that the index set is not endowed a priori with any topology. Following the ideas there developed, we base our approach on the association of the switched nonlinear system with a perturbed control system whose disturbances take values in a compact set. Once this association is performed, we obtain a straightforward proof of the converse theorem above by extending the results about IOSS obtained in (Krichman et al., 2001).
The outline of the paper is as follows. In section II we give the basic definitions including those of switched system, uniform input-output-to-state stability (UIOSS), uniform input-output-to-state-stability Lyapunov functions, etc. In section III we associate a perturbed control system with outputs whose disturbances take values in a compact set, with a class of switched nonlinear systems, and based on this association we prove the converse Lyapunov theorem. In section IV we introduce the notion of norm-estimator, and prove its existence for that class of switched nonlinear systems. Finally, in section V we present some conclusions.
II. SWITCHED SYSTEMS AND UIOSS Here we introduce some notations and definitions that will be used in the sequel. We denote with  the usual n-dimensional Euclidean space, and with
the usual n-dimensional Euclidean space, and with  its Euclidean norm.
its Euclidean norm.  stands for the closed ball of radius r around the origin in
stands for the closed ball of radius r around the origin in  . The set of measurable locally essentially bounded functions
. The set of measurable locally essentially bounded functions  is denoted by
is denoted by 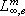 ; for each t ³ 0 and each
; for each t ³ 0 and each  we denote with wt the truncation of w at t, i.e., wt(t) = w(t) if t £ t, and wt(t) = 0 if t > t, and
we denote with wt the truncation of w at t, i.e., wt(t) = w(t) if t £ t, and wt(t) = 0 if t > t, and  .
.
Following standard terminology (Hahn, 1965), a continuous function 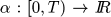 is positive definite if a(0) = 0 and a(r) > 0 whenever r > 0, and is of class
is positive definite if a(0) = 0 and a(r) > 0 whenever r > 0, and is of class  if in addition it is strictly increasing. A
if in addition it is strictly increasing. A 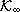 -class function a is a function of class
-class function a is a function of class  , defined in [0, +¥) that verifies
, defined in [0, +¥) that verifies  . A continuous function
. A continuous function  is a
is a  -class function if for any fixed t,
-class function if for any fixed t,  is of class
is of class  , and for a fixed r,
, and for a fixed r,  is decreasing and
is decreasing and  .
.
Let the family  , where G is an index set and fs are locally Lispchitz,
, where G is an index set and fs are locally Lispchitz,  and the fixed output function h, is of class
and the fixed output function h, is of class  and h(0) = 0.
and h(0) = 0.
We will assume in the sequel, with no loss of generality, that there is a one to one correspondence between the elements of G and the pairs of  , i.e., given s ¹ s' elements of G, then
, i.e., given s ¹ s' elements of G, then  . Given the family
. Given the family  , we consider the switched system with outputs
, we consider the switched system with outputs
 | (2) |
where 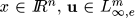 and s is a switching signal, i.e., s is a piecewise constant function
and s is a switching signal, i.e., s is a piecewise constant function  ; we will denote by
; we will denote by  the family of the switching signals of a given switched system. Associated with each
the family of the switching signals of a given switched system. Associated with each 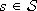 there is a sequence of real numbers
there is a sequence of real numbers  and a sequence of indexes
and a sequence of indexes  such that s(t) = sk for all tk £ t < tk+1. We recall that a trajectory of (2) corresponding to
such that s(t) = sk for all tk £ t < tk+1. We recall that a trajectory of (2) corresponding to 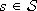 and originating from
and originating from  , is a locally absolutely continuous curve
, is a locally absolutely continuous curve  , such that h(0) = x and
, such that h(0) = x and 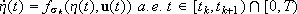 . Then, since the members of
. Then, since the members of  are locally Lipschitz, for each
are locally Lipschitz, for each 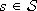 , each initial condition
, each initial condition  and each control
and each control  there exists a unique maximally defined trajectory corresponding to s, x and u. We denote this curve and its maximal interval of definition by x(t,x,u,s) and
there exists a unique maximally defined trajectory corresponding to s, x and u. We denote this curve and its maximal interval of definition by x(t,x,u,s) and  respectively. We will also use the notation
respectively. We will also use the notation  , and, when clear from the context, we will write y(t) instead of y(t,x,u,s).
, and, when clear from the context, we will write y(t) instead of y(t,x,u,s).
Definition II..1 The system (2) is uniformly (with respect to 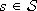 ) input-output-to-state stable, (UIOSS) if there exist a
) input-output-to-state stable, (UIOSS) if there exist a  -function b and
-function b and  -functions g1 and g2 such that, for each input
-functions g1 and g2 such that, for each input  and each
and each  , it holds that
, it holds that
 (3)
(3)
for each  and for all
and for all 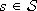 .
.
It follows from the definition above that a necessary, but not sufficient, condition for the UIOSS of the switched system (2) is each subsystem

of the family  be IOSS.
be IOSS.
In order to establish sufficient conditions for the UIOSS of (2), we introduce the following:
Definition II..2 A positive definite radially unbounded smooth (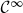 ) function
) function  is a common IOSS-Lyapunov function for
is a common IOSS-Lyapunov function for  if there exists a
if there exists a 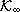 -function a and two
-function a and two  -functions c and g that verify:
-functions c and g that verify:
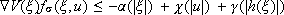 (4)
(4)
for all  , s Î G and
, s Î G and 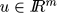 .
.
As pointed out in the Introduction, it can be easily shown, with similar arguments to those used in (Krichman et al., 2001), that the existence of a common IOSS-Lyapunov function V for  assures that the system (2) is UIOSS, i.e.,
assures that the system (2) is UIOSS, i.e.,
Theorem II..1 Suppose that there exists a common IOSS Lyapunov function for  . Then the system (2) is UIOSS.
. Then the system (2) is UIOSS.
III. A CONVERSE LYAPUNOV THEOREM
The question naturally arises whether the converse to Theorem II..1 holds.
In order to assure the existence of a common IOSS-Lyapunov function for  , we consider the family
, we consider the family  of mappings associated with
of mappings associated with  ,
, 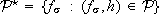 and assume that this family verifies the following condition:
and assume that this family verifies the following condition:
C The family  is uniformly locally Lipschitz, i.e., for each
is uniformly locally Lipschitz, i.e., for each  there exists lN ³ 0 such that
there exists lN ³ 0 such that
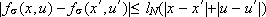
for all 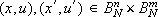 and all s Î G.
and all s Î G.
The main theorem of this paper may be stated as follows:
Theorem III..1 Suppose  satisfies C. Then if system (2) is UIOSS there exists a common IOSS-Lyapunov function V for
satisfies C. Then if system (2) is UIOSS there exists a common IOSS-Lyapunov function V for  .
.
The following result will be useful in the proof of Theorem III..1, since it establishes the connection between switched systems and perturbed controlled nonlinear systems.
Theorem III..2 Suppose  verifies C. Then there exist a compact metric space D, an injective function i : G ® D and a continuous function
verifies C. Then there exist a compact metric space D, an injective function i : G ® D and a continuous function  such that:
such that:
- i(G) is dense in D.
- F(x,u,d) is locally Lipschitz on (x,u) uniformly on d, i.e., for each compact subset K of
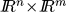 there is some constant cK so that
there is some constant cK so that 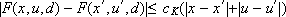 , for all (x,u), (x',u') Î K, and all d Î D.
, for all (x,u), (x',u') Î K, and all d Î D. - F(x,u,i(s)) = fs(x,u) for all
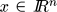 , all
, all 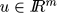 and all s Î G.
and all s Î G.
Proof: Since the family  is equibounded due to the condition C and to the fact that fs(0,0) = 0 for all s Î G, the theorem can be proved following the same steps of the proof of Theorem 3.2 of Mancilla Aguilar and García, (2000).
is equibounded due to the condition C and to the fact that fs(0,0) = 0 for all s Î G, the theorem can be proved following the same steps of the proof of Theorem 3.2 of Mancilla Aguilar and García, (2000).
Remark III..1 It is clear that when G is a finite set the family  satisfies C. In this case we can take D = G endowed with the discrete metric, i the identity map and F(x,u,s) = fs(x,u) for all
satisfies C. In this case we can take D = G endowed with the discrete metric, i the identity map and F(x,u,s) = fs(x,u) for all 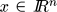 , all
, all 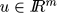 and all s Î G.
and all s Î G.
Consider F, D and i as in Theorem . We denote with  and with
and with  the subset of elements of
the subset of elements of 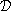 that are piecewise constant i(G)-valued functions, and associate to the switched system (2) the following perturbed control system with outputs:
that are piecewise constant i(G)-valued functions, and associate to the switched system (2) the following perturbed control system with outputs:
 | (5) |
where the state z evolves in  , the output y in
, the output y in 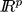 , the control u belongs to
, the control u belongs to 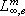 and the disturbance d to
and the disturbance d to 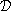 .
.
Given  ,
,  and
and  , if we denote with z(t,x,u,d) the maximally defined trajectory of (5) originating from x with control u and disturbance d, and with
, if we denote with z(t,x,u,d) the maximally defined trajectory of (5) originating from x with control u and disturbance d, and with  its maximal interval of definition then, as consequence of Theorem , the following hold:
its maximal interval of definition then, as consequence of Theorem , the following hold:
- For each
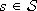 , if
, if  , then
, then 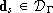 ,
,  and
and  .
. - For each
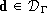 , there exists a unique switching signal s such that
, there exists a unique switching signal s such that  .
.
Remark III..2 We conclude from Theorem that a switched system with outputs whose associated family  verifies C can be considered as a perturbed control system with outputs whose disturbances are piecewise constant functions that take values in a dense subset of a compact metric space D.
verifies C can be considered as a perturbed control system with outputs whose disturbances are piecewise constant functions that take values in a dense subset of a compact metric space D.
The following result will be used in the sequel:
Proposition III..1 Suppose that  ,
,  and
and  and let
and let 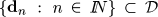 such that
such that  a.e. Then if
a.e. Then if  is defined on [0, t],
is defined on [0, t],  is also defined on [0, t] for n large enough and, in addition,
is also defined on [0, t] for n large enough and, in addition,  for all t Î [0, t].
for all t Î [0, t].
Proof: It follows with arguments similar to those in the proof of Proposition 3.1 in (Mancilla Aguilar and García, 2000).
In the following lemma we show that the perturbed control system (5) has the same stability properties as the switched system (2).
Lemma III..1 Suppose the family  verifies C. If the switched system (2) is UIOSS, then the perturbed control system (5) is uniformly (with respect to
verifies C. If the switched system (2) is UIOSS, then the perturbed control system (5) is uniformly (with respect to  ) IOSS, i.e., there exist a function b of class
) IOSS, i.e., there exist a function b of class  and functions g1 and g2 of class
and functions g1 and g2 of class  such that, for each input
such that, for each input  and each initial state
and each initial state  , it holds that
, it holds that
 (6)
(6)
for all 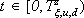 and all
and all  .
.
Proof: Suppose that  and
and  . Due to the density of i(G) in D, there exists a sequence
. Due to the density of i(G) in D, there exists a sequence  such that
such that  a.e. (see (Mancilla Aguilar and García, 2000) for details).
a.e. (see (Mancilla Aguilar and García, 2000) for details).
Let t such that z(t, x, u, d) is defined for all t Î [0, t]. Then due to Proposition , for all t Î [0, t],  .
.
If (3) holds, then 

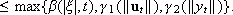
Remark III..3 We recall that a positive definite radially unbounded  function
function  is an UIOSS-Lyapunov function for system (5) if there exist a function a of class
is an UIOSS-Lyapunov function for system (5) if there exist a function a of class 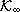 and two functions c and g of class
and two functions c and g of class  verifying:
verifying:
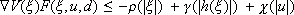
for all  , all d Î D and all
, all d Î D and all 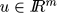 .
.
It follows that if C holds for the family  , then V is an UIOSS-Lyapunov function for system (5) with r and c as above if and only if it is a common IOSS-Lyapunov function for
, then V is an UIOSS-Lyapunov function for system (5) with r and c as above if and only if it is a common IOSS-Lyapunov function for  .
.
Due to this last remark, Theorem III..1 is a corollary of the following:
Theorem III..3 Suppose system (5) is UIOSS. Then there exist a smooth UIOSS-Lyapunov function for it.
Proof: Since system (5) is UIOSS then, due to Theorem 1 in Krichman et al., 2001, (which holds, with minor modifications of its proof if the disturbance set is a compact metric space instead of [-1, 1]p,  ), there exists a smooth UIOSS-Lyapunov function for (5).
), there exists a smooth UIOSS-Lyapunov function for (5).
IV. NORM-ESTIMATORS
In this section we prove that the existence of a common IOSS Lyapunov function for the family  implies the existence of a norm-estimator for the switched system (2) in the following sense.
implies the existence of a norm-estimator for the switched system (2) in the following sense.
Definition IV..1A (uniform with respect to the switching signal) state norm-estimator for a switched system (2) (briefly, a norm-estimator for (2)) is a pair (S, r), where r is a function of class 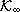 and S is a system
and S is a system
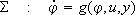 (7)
(7)
evolving in  and driven by the controls and outputs of (2), such that the following conditions are satisfied:
and driven by the controls and outputs of (2), such that the following conditions are satisfied:
-
 is continuous and locally Lispchitz on j uniformly on (u, y).
is continuous and locally Lispchitz on j uniformly on (u, y). - There exist
 -functions
-functions 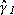 and
and  and a function
and a function 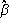 of class
of class  such that for any initial state
such that for any initial state  , all inputs
, all inputs  and
and  , and any t in the interval of definition of the solution
, and any t in the interval of definition of the solution  , the following holds:
, the following holds:
 (8)
(8)
that is, (7) is ISS with respect to u and y (considered as inputs). - There is a function b Î
 such that, for any pair of initial states x and z of (2) and (7) respectively, any control
such that, for any pair of initial states x and z of (2) and (7) respectively, any control  and any switching signal
and any switching signal 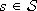 , it holds that
, it holds that
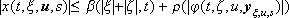 (9)
(9)
for all , where yx,u,s denotes the output trajectory of (2), that is, y(t,x,u,s).
, where yx,u,s denotes the output trajectory of (2), that is, y(t,x,u,s).
A. Construction of a norm-estimator for (2)
In order to construct a norm-estimator for (2), we need the following lemma whose proof is similar to the one of Lemma 5.2 of (Krichman et al., 2001)
Lemma IV..1 Suppose V is a common IOSS-Lyapunov function for  . Then there exists a
. Then there exists a 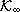 -function q and
-function q and  - functions c1 and c2 such that the function
- functions c1 and c2 such that the function 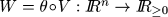 is of class
is of class  , positive definite, radially unbounded and verifies
, positive definite, radially unbounded and verifies
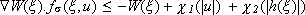 (10)
(10)
for all  ,
, 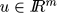 and s Î G.
and s Î G.
The norm-observer is then obtained as follows.
Theorem IV..1 Suppose that verifies condition C. Then, if the switched system (2) is UIOSS, it admits a norm-estimator.
verifies condition C. Then, if the switched system (2) is UIOSS, it admits a norm-estimator. Proof: From Theorem and Lemma there exists a positive definite and radially unbounded function W of class  that verifies (10). Due to the positive definiteness and radial unboundedness of W, there exist
that verifies (10). Due to the positive definiteness and radial unboundedness of W, there exist 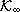 -functions a1 and a2 such that
-functions a1 and a2 such that
 (11)
(11)
for all  . We assume, with no loss of generality that r £ a2(r) for all r > 0.
. We assume, with no loss of generality that r £ a2(r) for all r > 0.
Consider the system S
 (12)
(12)
with c1 and c2 as in (10).
Since system (12) is ISS with respect to u and y, (it can be seen as an exponentially stable linear system driven by the "input"  ), the inequality (8) trivially holds.
), the inequality (8) trivially holds.
Let any initial states x and z of (2) and (12) respectively, any control  and any switching signal
and any switching signal 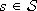 , and consider the resulting trajectory (x(t), j(t)) of the composite system
, and consider the resulting trajectory (x(t), j(t)) of the composite system

with initial condition (x(0), j(0)) = (x, z). It is easy to see that the maximal interval of definition of this trajectory is  ; then, due to property (10), we have
; then, due to property (10), we have

 . Then,
. Then,

since r £ a2(r) and 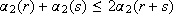 for all r, s ³ 0. Then, and due to (11),
for all r, s ³ 0. Then, and due to (11),
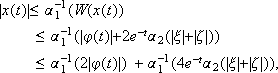
as  for all r, s ³ 0. Finally, if we take
for all r, s ³ 0. Finally, if we take 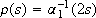 and
and 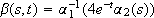 , r is of class
, r is of class 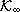 , b is of class
, b is of class  and
and
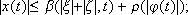
in consequence (9) holds and the proposed pair is a norm-estimator for (2).
CONCLUSIONS
In this paper we have proved the existence of a norm-estimator for a certain class of IOSS switched systems as a byproduct of a converse Lyapunov theorem for this class of IOSS systems. The proof of the theorem is based on the association of these system with perturbed nonlinear control systems, and on simple generalizations of results on a converse Lyapunov theorem for IOSS systems with bounded time-varying perturbations.
REFERENCES
1. Hahn, W., Stability of Motion, Springer-Verlag, New York, (1967). [ Links ]
2. Jiang, Z. P. and L. Praly, "Preliminary results about robust Lagrange stability in adaptive nonlinear regulation", Int. J. of Adaptive Control and Signal Processing 6, 285-307 (1992). [ Links ]
3. Krichman, M., E. D. Sontag and Y. Wang, "Input-output-to-state stability", SIAM J. Control 39, 1874-1928 (2001). [ Links ]
4. Liberzon D. and A. S. Morse, "Basic problems in stability and design of switched systems", IEEE Contr. Syst. Mag. 19, 59-70 (1999). [ Links ]
5. Mancilla Aguilar J. L. and R. A. García, "A converse Lyapunov theorem for nonlinear switched systems", Systems Contr. Lett. 41, 67-71 (2000). [ Links ]
6. Mancilla Aguilar, J. L. and R. A. García, "On converse Lyapunov theorems for ISS and iISS switched nonlinear systems", Systems Contr. Lett., 42 47-53 (2001). [ Links ]
7. Praly, L. and Y. Wang, "Stabilization in spite of matched unmodeled dynamics and an equivalent definition of input-to-state stability", Math. Control Signals Systems 9, 1-33 (1996). [ Links ]
8. Sontag, E. D. and Y. Wang, "Output-to-state stability and detectability of nonlinear systems", Systems Contr. Lett. 29, 279-290 (1997). [ Links ]














