Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.33 n.4 Bahía Blanca oct./dic. 2003
Control of the reaching mode in variable structure systems
R. J. Mantz1, H. De Battista2, F. D. Bianchi2 and R. D. Fernández3
LEICI, Dto. de Electrotecnia, Facultad de Ingeniería, UNLP, C.C.91 (1900) La Plata, Argentina
1 UNLP-CICpBA, mantz@fisica.unlp.edu.ar
2 UNLP-CONICET, deba@fisica.unlp.edu.ar, fbianchi@volta.ing.edu.ar
3 UNLP-UNPSJB, rfernand@fisica.unlp.edu.ar
Abstract ¾ This paper focuses on the behaviour of variable structure systems with dynamic control, particularly during the reaching mode of operation. It is shown that stability problems may arise during this reaching phase. The causes of these problems are closely related with the problems of windup commonly found in conventional control systems with actuator constraints. Methods for stabilization of the reaching mode are proposed which are based on the concepts of 'realizable reference' and observers. Well-known algorithms that have been previously proposed from empiric ideas, can now be rigorously derived using these concepts. The theoretical framework developed by Kothare and co-workers in the context of windup is generalized to study and design control algorithms for the reaching mode.
Keywords ¾ Reaching Mode. Sliding Mode. Variable Structure Systems. Windup.
I. INTRODUCTION
It is well-known that variable structure systems (VSS) undergoing sliding motions are robust to parameter uncertainties and external disturbances. Moreover, the order of the dynamic system is reduced during the sliding mode, and the sliding dynamics becomes dependent on the designer-chosen sliding surface (Utkin, 1978; Sira-Ramírez, 1988, 1996; Hung et al., 1993).
Actually, the complete response of a VSS comprises two phases or operating modes: the reaching mode (RM) and the sliding mode (SM). Even though the latter has been more discussed in literature, the former is not less important when the global performance is considered. Different approaches to the RM problem can be found in Hung et al. (1993). Despite their outstanding contributions, these approaches do not focus on the state dynamics (Hung et al., 1993; Mantz et al., 2001) and, in general, are particular or intuition-based solutions.
This paper studies a particular behaviour that may lead to a serious degradation and, moreover, instability of the RM, deteriorating the global performance of the VSS. The work puts special emphasis on VSS with dynamic controllers where this undesirable behaviour is more evident. This degradation of the RM is linked in the paper to another problem extensively studied in the last years: windup (Fertik and Ross, 1967; Doyle et al., 1987; Astrom and Rundqwist, 1989; Peng et al., 1996; Romanchuk, 1999; Wu and Grigoriadis, 1999). Based on this connection between both problems, different methods of RM compensation are proposed. They make use of the concepts of realizable references and observers. Moreover, the unified theoretical framework proposed by Khotare et al. (1994) to address the problem of windup is generalized to solve the RM problem in VSS.
In the following section, the problem is posed and illustrated through an example. Then, the similarities among windup and RM problems are stressed. In subsection II.B., a pair of RM compensation algorithms based on the concepts of realizable references and observers are derived. At the end of the section, the framework developed by Khotare and co-workers is generalized to address the RM problem. Finally, the conclusions of the paper are summarized.
II. PROBLEM FORMULATION AND MAIN RESULTS
A. Problem formulation
Figure 1 shows a schematic diagram of a variable structure controlled system. P is the process to control. The block D takes into consideration the parametric uncertainties. The switch L is driven by the output of the controller K, namely s(x). It is assumed that K may include a dynamic expansion to reject steady state disturbances (Utkin, 1999) (obviously, it is not possible to include in K a dynamic expansion to reduce chattering problems (Sira-Ramírez, 1993), which must be inserted at the input of P). Then, s(x) depends on the state variables of the process (xs) and of K (xk). It is also assumed that K is an LTI system, which is an usual election in most applications (some non-linear process functions y = f(xs) can be explicitly chosen as inputs of K to consider the case of non-linear processes). Then, K(s) = C(sI - A)-1B + D. Hereinafter, the following conventional notation will be used:
 | (1) |
where v = [r y xxT]T is the input vector.
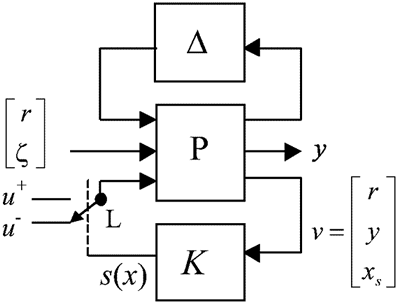
Figure 1: Variable structure system.
The objective of the sliding mode control is enforcing the system state to evolve on the surface defined by s(x) = 0. This surface is chosen to satisfy the problem specifications such as dynamic behaviour, robustness against state disturbances z and model uncertainties, etc..
When the system operates in sliding mode, i.e.:
 | (2) |
the equivalent continuous control ueq(v, xk) can be defined. This fictitious signal produces the same dynamic behaviour than the actual discontinuous control u(t) switching, ideally, at infinite frequency. A necessary and sufficient condition for the existence of SM is that (Sira-Ramírez, 1988)
u- £ ueq £ u+ (3)
being u+ and u- the extreme values of the control variable.
Obviously, all the robust properties of variable structure control are valid during the sliding regime. Then, it is essential that the SM predominates over the RM. With this purpose, it is necessary to reduce the reaching time as much as possible.
In fact, during the RM, the P - K loop is opened. Thus, the process and controller dynamics evolve independently of each other. Consequently, this lack of correspondence during the reaching phase can degrade the global performance of the VSS. Clearly, this degradation is greater when the state trajectory reaches the sliding surface outside the sliding domain (i.e. at a point where the available control effort is not sufficient to establish the SM). When this occurs, the state trajectory cannot be confined to the surface and crosses it. Hence, the RM and, consequently, the open loop operation is prolonged. Note that the sliding domain could be extended increasing the available controls u+ and u-. However, specially in nonlinear systems, this possible solution usually stresses the problem because the state motion during the RM directly depends on u+ and u-. In other words, the increase in the available control values may accentuate the lack of correspondence between the states of P and K, which is necessary to establish a sliding regime.
Example. Consider the system
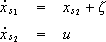 | (4) |
to be controlled by SM. To reject a constant disturbance z, an integral state is included in K:
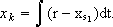 | (5) |
Furthermore, the following control law is selected:
 | (6) |
where kT = [ ks1 ks2 -kk ], is calculated to obtain overdamped dynamic behaviour. The rate of gains 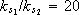 and
and 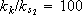 are selected to assign both SM closed-loop eigenvalues at -10.
are selected to assign both SM closed-loop eigenvalues at -10.
Figure 2 shows the step responses of the output variable 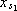 , the surface coordinate s, and the integral state xk, respectively.
, the surface coordinate s, and the integral state xk, respectively.
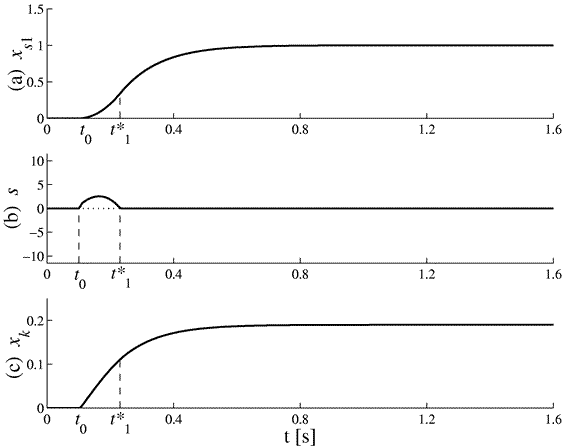
Figure 2: Step response of the system when U = 40: (a) output variable, (b) surface coordinate, (c) integral state.
The satisfactory behaviour of the system is explained by the following:
- The sliding surface is properly chosen, with a pole assignment according to specifications.
- The available control action (U = 40) allows a rapid reaching of the surface inside the sliding domain, guaranteing that the SM predominates over the RM during the transient response.
Consider now the same dynamical system with a reduction in the available control which can be ascribed to an actuator constraint or to a fault. Independently of the current example, and as it can be inferred from many papers regarding VSS, it is expected a degradation in the global performance of the system caused by a longer reaching phase. This problem may result seriously magnified if the sliding surface is reached outside the sliding domain. In fact, the reaching mode is prolonged in this case until the surface is finally reached where the SM existence condition holds. This situation is depicted in Fig. 3. The curves show the time evolution of the output signal, the surface coordinate and the integral state when the available control falls to U = 26.

Figure 3: Step response of the system when U = 26: (a) output variable, (b) surface coordinate, (c) integral state.
Occasionally, this deterioration in the RM may lead to instability of the VSS. Obviously, as the sliding surface is chosen Hurwitz, the instability of the VSS is caused by the RM. This case is sketched in Fig. 4. It shows the step response of the system when the available control falls further to U = 24.7. It is evident from this figure that the RM is unstable and, consequently, that the sliding regime will never be established. As it is discussed in the following, this undesirable behaviour is directly connected with the dynamic control and the open-loop operation during the RM.
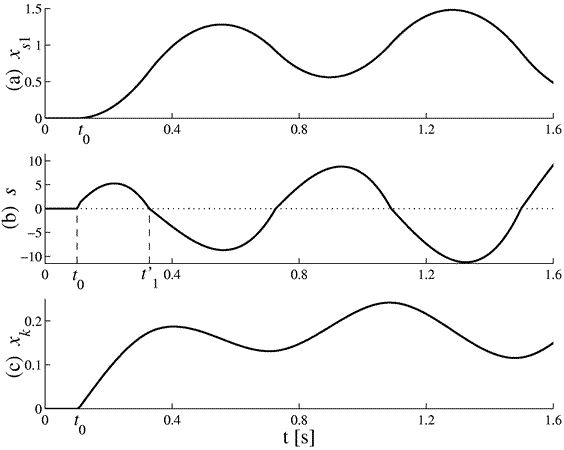
Figure 4: Step response of the system when U = 24.7: (a) output variable, (b) surface coordinate, (c) integral state.
It should be remarked that the plant P in the example has been chosen linear in order to avoid superimposing effects that may dissimulate the problem under analysis.
Clearly, the dissimilar behaviour put in evidence in Figs. 2-4 is exclusively due to the difference between the reaching phases. To understand the low proficiency achieved with conventional RM, Fig. 3 is analyzed in detail. Note that:
- When the reference changes at t0 = .1s, s(x) takes a positive value. Then, the actuator provides the maximum control effort +U. This value is not sufficient to maintain the SM and the P - K control loop is opened. It is observed that although s(x) > 0, the integral state xk grows and, consequently, s(x) increases. That is, the actuator oversaturates, as in typical windup behaviour, and the trajectory moves away from the surface.
- At t1=.32s the state reaches the surface s(x) = 0, but outside the sliding domain. Clearly, although s(x) there is no correlation among the state variables to verify
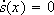 . Hence, the sliding regime cannot be imposed.
. Hence, the sliding regime cannot be imposed. - The previous situation is repeated several times until the SM is definitively established in t2 = 1.08s. The global performance of the VSS (RM+SM) is mainly determined by the RM because it is dominant with respect to the SM. Hence the undesirable response.
The magnification of these effects when the available control is further reduced from U = 26 to U = 24.7 is the cause of the system instability shown in Fig. 4.
B. Proposed compensation for the RM
It is stated above that the undesirable global performance is not attributable to the SM but to the RM. In fact, the sliding regime guarantees a stable behaviour. Then, a correction solely for the RM is proposed here. That is, the proposed compensation fits into the well-known two-step correction methods (Kothare et al., 1994; Peng et al., 1996):
- Firstly, a sliding surface to guarantee the control requirements is designed ignoring the physical limitations.
- Then, a compensation is incorporated to the conventional RM approach.
This additional compensation must satisfy the following specifications:
- stability,
- action during the RM exclusively, i.e. when the limitation is active,
- graceful degradation with respect to the unrestricted control system (i.e. the control system with insignificant or no RM).
After enclosing the problem into the context of windup, some control algorithms for the RM can readily be derived from anti-windup concepts. In the following subsections, a pair of control strategies are developed.
B.1. Conditioning technique to RM approach
The concept of realizable reference introduced by Hanus et al. (1987) in the context of windup (Walgama et al., 1992; Peng et al., 1996), is here used to derive RM compensation algorithms. The basic idea is to modify the controller input with the aim of restoring the consistency between K and the input of the process. The modified input is called realizable reference (rr). The proposed modification is such that if the realizable reference had been applied to K, the system would have always operated in sliding regime. Thus, exciting the controller K:
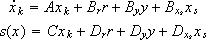 | (7) |
with rr yields
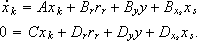 | (8) |
Then, rr must verify
s(x) = Dr(r - rr), (9)
or, equivalently
 (10)
(10)
Replacing r in the state equation of K (7) by the realizable reference rr (10) (as Hanus et al. (1987) in the conditioning technique), yields
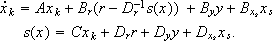 | (11) |
Thus, the compensated controller for the RM is given by
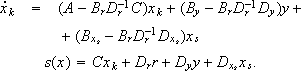 | (12) |
Comparing the dynamics of s(x) for the conventional RM:
 (13)
(13)
and for this new approach:
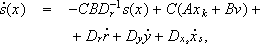 | (14) |
it is possible to see that an additional term appears. This term improves the stability of the reaching mode provided  .
.
Observation: RM approaches similar to that given by Eqn. (14) can be found in the literature (Hung et al., 1993). However, the value of the present result lies on the fact that it is deduced from a general theoretic framework.
Example (continued). Figure 5 depicts the time evolution of the system output, the surface coordinate and the integral state of the system (4)-(6) (when U = 24.7) with the RM compensation developed in this section. For the sake of comparison, the curves of Fig. 4 depicting the unstable response of the system without RM compensation are repeated with thin trace in Fig. 5. It can be observed a significant improvement in the VSS response when the RM compensation is applied. In contrast with the conventional RM (i.e. without compensation), the proposed approach reduces s(x) in spite of the increasing xk. This fact permits a rapid convergence of s(x) to zero at 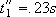 . As the period of open-loop operation is short, the surface is reached at a point inside the sliding domain. Consequently, the system operates in sliding regime from
. As the period of open-loop operation is short, the surface is reached at a point inside the sliding domain. Consequently, the system operates in sliding regime from 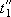 , eliminating the risk of oscillations and instability. Effectively, as the SM dominates in the transient response, the VSS global response is practically in accordance with the desired dynamics (i.e. with the pair of eigenvalues assigned at -10).
, eliminating the risk of oscillations and instability. Effectively, as the SM dominates in the transient response, the VSS global response is practically in accordance with the desired dynamics (i.e. with the pair of eigenvalues assigned at -10).
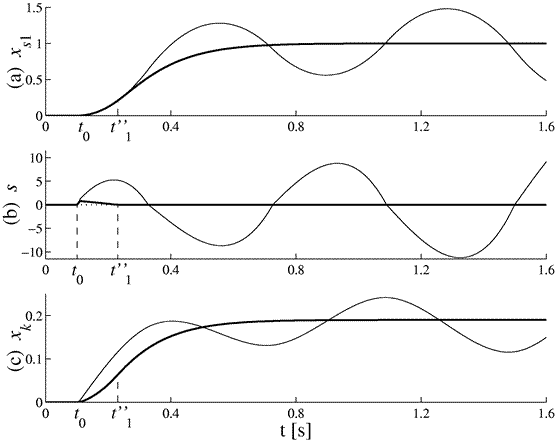
Figure 5: Step response of the system when U = 24.7 with RM correction (thick trace) and without it (thin trace): (a) output variable, (b) surface coordinate, (c) integral state.
B.2. Observer-based RM compensation
As it was aforementioned, the process input during the RM is independent of the state and/or output of K (open-loop operation). Then, although the sign of s(x) forces the state motion towards the surface, the internal evolution of K can extend the reaching time. Moreover, the state trajectory can be driven towards points outside the sliding domain. In this section, it is proposed to improve the conventional RM by estimating the state of K, according with the presence of the non linear actuator in a similar way as suggested by Astrom and Rundqwist (1989) in their observer-based anti-windup method. Then, the estimation of the state is included in K:
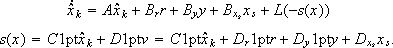 | (15) |
Finally, the resulting RM control equations are:
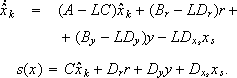 | (16) |
In order to evaluate the effects of the introduced compensation, the dynamics of s(x) for the conventional RM:
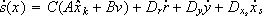 (17)
(17)
and the proposed observer-based RM correction:
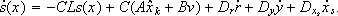 (18)
(18)
are compared. It is seen that the proposed correction introduces the stabilizable term -CLs(x), with CL ³ 0.
From Eqn. (14) and Eqn. (18), it follows immediately that the RM compensation strategy based on the conditioning technique (Peng et al., 1996) is a particular solution of the observer-based RM approach ( ).
).
B.3. Theoretical framework to the study and design of RM compensation algorithms
The importance of the close connection between the problems of RM and windup lies on the possibility of applying classical solutions and more recent progresses in the control theory of systems with constraints to improve the RM of VSS. Hence, a new general methodology to design RM compensations is proposed for VSS which is in correspondence with the unified framework proposed by Kothare et al. (1994) to study and design anti-windup algorithms.
Then, to improve the system behaviour during the RM, a correction 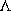 to the feedback block K of Fig. 1 is proposed (Fig. 6). Assuming that the sliding surface has been chosen according to the control specifications, the correction of the state and output of K (x1 and x2, respectively) must only be active during the RM. That is
to the feedback block K of Fig. 1 is proposed (Fig. 6). Assuming that the sliding surface has been chosen according to the control specifications, the correction of the state and output of K (x1 and x2, respectively) must only be active during the RM. That is
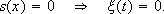 (19)
(19)
To assure the compensated controller 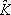 can also be realized as an LTI system,
can also be realized as an LTI system, 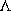 is assumed causal and LTI.
is assumed causal and LTI.

Figure 6: Variable structure system with proposed RM correction.
The sliding dynamics, obtained by the discontinuous action as well as by the equivalent control, can also be accomplished by a saturated actuator with gain k ® ¥ (Utkin, 1999). This allows to define, in the context of RM, a saturation error equivalent to the one used in all anti-windup methods (Kothare et al., 1994; Peng et al., 1996):
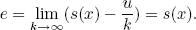 | (20) |
Then,
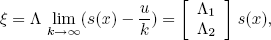 | (21) |
where the elements  and
and 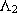 of
of 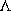 are static gains in order to satisfy (19).
are static gains in order to satisfy (19).
Following the Kothare et al. (1994) proposal to design anti-windup algorithms, a parameterization of the reaching mode algorithms as function of two parameters H1 and H2 is suggested. Thus, incorporating 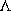 and K into
and K into 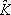 results
results
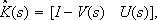 (22)
(22)
where
 | (23) |
are the left coprime factors of K(s) = V-1(s)U(s) and
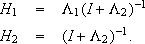 | (24) |
Comparing Eqn. (12) with Eqn. (23), the following parameters can readily be recognized:
 | (25) |
Then, these parameters characterize the algorithm for RM compensation based on the concepts of realizable reference which ,was deduced in subsection II..
On the other hand, the parameters characterizing the RM compensation algorithm based on the observer (subsection II.) are obtained from Eqn. (16):
| H1 = L | (26) |
| H2 = I. |
III. CONCLUSIONS
Robustness is a well-known feature of VSS operating in SM. Then, it is essential that the SM predominates over the RM where the system behaves as an open loop. The reduction of the available control action not only can degrade the reaching phase (and, consequently, the global performance of the VSS) but it also may lead to instability. These undesirable effects are particularly common in VSS (linear and nonlinear) with dynamic control. The problem of stability during the RM is addressed in this paper as a problem of windup. That is, it is fitted into the context of systems with actuator constraints. Based on the ideas of anti-windup, different approaches to the RM problems are investigated. Compensation algorithms for the RM have therefore been developed which are based on the conditioning technique and the observers theory. Furthermore, the theoretical framework proposed by Khotare et al. (1994) has been generalized to the problem of RM in VSS.
ACKNOWLEDGEMENTS
This work was supported by the Comisión de Investigaciones Científicas CIC, the Agencia de Promoción Científica y Técnica ANPCyT, the Consejo Nacional de Investigaciones Científicas y Técnicas CONICET and the Universidad Nacional de La Plata.
REFERENCES
1. Astrom K.J. and L. Rundqwist, "Integrator windup and how to avoid it", Proc. of the American Control Conference, Pittsburgh, USA, 1693-1698 (1989). [ Links ]
2. Doyle J., R. Smith and D. Enns, "Control of plants with input saturation nonlinearities", Proc. of the American Control Conference, Minneapolis, USA, 1034-1039 (1987). [ Links ]
3. Fertik H. and C. Ross, "Direct digital control with anti-windup feature", ISA Transactions, 6, 317-328 (1967). [ Links ]
4. Hanus R., M. Kinnaert, and J. Henrotte, "Conditioning technique, a general anti-windup and bumpless transfer method", Automatica, 23, 6, 729-739 (1987). [ Links ]
5. Hung J.Y., W. Gao and J.C. Hung, "Variable structure control: a survey", IEEE Transactions on Industrial Electronics, 40, 1, 2-22 (1993). [ Links ]
6. Kothare M., P. Campo, M. Morari and K. Nett, "A unified framework for the study of anti-windup design", Automatica, 30, 12, 1869-1883 (1994). [ Links ]
7. Mantz R.J., H. De Battista, and P.F. Puleston, "A new approach to reaching mode of VSS using trajectory planning", Automatica, 37, 5, 763-767, (2001). [ Links ]
8. Peng Y., D. Vrancic and R. Hanus, "Anti-windup, bumpless, and CT techniques for PID controllers", IEEE Control Systems Magazine, 8, 1, 48-56 (1996). [ Links ]
9. Romanchuk B., "Some comments on anti-windup synthesis using LMIs", International Journal of Robust and Nonlinear Control, 9, 717-734 (1999). [ Links ]
10. Sira-Ramírez H., "Differential geometric methods in variable structure control", International Journal of Control, 48, 4, 1359-1390 (1988). [ Links ]
11. Sira-Ramírez H., "On the dynamical sliding mode control of nonlinear systems", International Journal of Control, 57, 5, 1039-1061 (1993). [ Links ]
12. Sira-Ramírez H., "On the sliding mode of multivariable nonlinear systems", International Journal of Control, 64, 4, 745-765 (1996). [ Links ]
13. Utkin V.Y., Sliding Mode and Their Application in Variable Structure Systems, MIR Publishers: Moscow, Rusia (1978). [ Links ]
14. Utkin V.Y., Sliding Mode Control in Electromechanical Systems, Taylor and Francis, London (1999). [ Links ]
15. Walgama K., S. Ronnback and J. Sternby, "Generalization of conditioning technique for anti-windup compensators", IEE Proceedings D, 139, 109-118 (1992). [ Links ]
16. Wu F. and K. Grigoriadis, "LPV-based control of systems with amplitude and rate actuator saturation constraints", Proc. of the American Control Conference, San Diego, USA, 3191-3195 (1999). [ Links ]














