Formulation and numeric calculation of non-isothermal effectiveness factor for finite cylindrical catalysts with bi-dimensional diffusion

Bibian Hoyos¹, Juan Guillermo Cadavid² and Hermes Rangel²

¹ Escuela de Procesos y Energía. Universidad Nacional de Colombia, A. A. 1027. Medellín, Colombia.
bahoyos@perseus.unalmed.edu.co
² Facultad de Ingeniería. Universidad Nacional de Colombia, Transv 38 Diag 40. Bogotá D. C., Colombia.
jcadavid@ing.unal.edu.co

Abstract — A model for calculating the effectiveness factor and the concentration and temperature profiles for finite cylindrical either hollow or solid catalyst particles is presented. The model accounts for dispersion in both radial and axial directions and non-isothermal behavior. The resulting differential partial equations system is discretized by a centered finite difference method and a program written for the Excel^™ electronic sheet solves the highly nonlinear algebraic system. The numerical technique can be extended for any kinetic expression; for illustration, some results for n-th order reactions rate expressions are shown.

Keywords — Effectiveness Factor. Finite Cylindrical Catalysts. Bi-Dimensional Dispersion. Non-Isothermal Model.

I. INTRODUCTION

In heterogeneous catalytic studies it is important to establish the mechanism that is limiting the overall rate of transformation within the catalytic particle, that is, to know whether the diffusive effects are controlling the process rate, or whether the chemical reaction at the particles surface controls.

To have an idea of the relative importance of diffusion and chemical reaction phenomenon, an effectiveness factor for catalytic particles is defined, for a steady state flow condition, as

(1)

which can also be expressed in terms of molar velocity through the external surface particle by

(2)

As stated by Eqn. 2, a value of unit for the effectiveness factor (for isothermal conditions) indicates that there are not diffusive barriers to the overall rate of transformation and the activation energy of the chemical reaction at the surface of the particle is the rate determinant step. An effectiveness factor less than unit shows that the diffusive effects are important in the control of global velocity of transformation: the smaller the effectiveness factor is, the larger importance of the physical processes of mass transfer are.

The case of an effectiveness factor greater than unit can also appear, which indicates that heat transfer effects are important, and even though in appearance this would be an ideal situation, in practice this is not recommendable due to catalytic deactivation originated by high temperatures within the particle.

There are a great number of published articles where the parameters of major influence in the effectiveness factor are studied. Among those parameters, the particle geometry is perhaps of major concern. In particular, the studies for cylindrical pores (Carberry, 1961), for spherical particles (Smith, 1956; Carberry, 1976), for flat slabs (Morbidelli et al., 1982a) for cylindrical pellets (Morbidelli et al., 1982b), and more recently, the investigation of Wang et al., (1994) for rectangular reticulated particles are remarkable. Doraiswamy and Sharma (1984) showed a good summary of the geometric influence in the effectiveness factor and in the concentration profiles inside the particle.

The influence of the kinetic expression for the chemical reaction in the effectiveness factor is also an aspect widely studied: there are studies for first and second order rate expressions (Wakao et al., 1978; Lee, 1979; Lin et al., 1986), for reactions type Langmuir-Hinsehelwood (Krasuk and Smith, 1965; Morbidelli et al., 1982a,b), for negative order rate expressions (Morbidelli and Varma, 1983) and even for multiple reactions (Wohlfahrt, 1982). Doraiswamy and Sharma (1984) , Satterfield and Sherwood (1963) and Satterfield (1991) also showed the analytic equations of effectiveness factor for a great number of reactions with highly complexes kinetic expressions.

Almost all works in literature consider in their mathematical models the diffusion phenomenon in axial direction only with non-isothermal behavior. To solve the differential equations system that these models generate, there are simplifications to special cases to allowing an analytical solution (Scott et al., 1984; Singh, 1985) or numerical solutions by using orthogonal collocation methods (Lin et al., 1986; Trotta and Guidice, 1985; Rusic and Zrncevic, 1994) and simulations with Montecarlo methods (Wang et al., 1994).

The mathematical models of non-isothermal diffusion in both radial and axial directions generate a partial differential equations system that had not been studied extensively. In this work it is shown the formulation of a mathematical model for effectiveness factor calculation in finite cylindrical particles (hollow or solid). Non-isothermal behavior and diffusion in radial and axial directions simultaneously are considered with reactions rate expressions in potential law. As a different alternative to those in literature, the partial differential equations system is solved simultaneously by the central finite differences method. The results of the model solution are compared with the data presented by Davis (1990) who utilized the DISPL computer program to solve the system of differential equations.

II. MATHEMATICAL MODEL

The mathematical model for the effectiveness factor calculation of hollow cylindrical pellets showed in this work, was developed by the application of mass and energy conservation equations around a volume differential element as shown in Fig. 1, with the following suppositions:

• Diffusion of substances in axial and radial directions simultaneously
• Non-isothermal situation
• Kinetic equation expressed by potential law, that is, velocity equations like:( -r_A ) = k * C_Aⁿ
• Chemical reactions without change in total moles number.
• Steady state.
• Constant properties of substances (D_e,A, k_e, ΔΗ_r, etc.).
• Temperature and concentration profile are concentric.

The last supposition was confirmed experimentally by Wakao et al., (1978) for chemical reactions of first order in spherical particles and the extension to cylindrical particles and kinetic expressions of higher order is supposed valid.

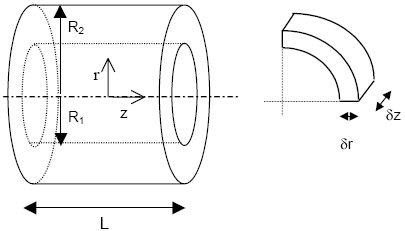
Fig. 1. Catalytic pellet with hollow cylindrical shape and volume differential element

By realizing a mass balance around the volume differential element of Fig. 1 and by applying the Fick's law for steady state, we obtain:

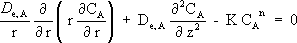(3)

With the following boundary conditions (taking the pellet's center as origin of coordinates):

An energy balance around the volume differential element in union with the Fourier's law under steady state conditions results in:

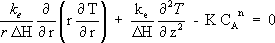(4)

The boundary conditions to solve the differential Eqn. 4 are:

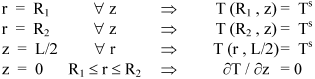
With the purpose of allowing the numerical solution of differential Eqns. 3 and 4; it is preferable to write them in function of dimensionless variables as:

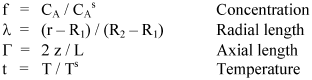
The mass balance equation in function of the new dimensionless variables is:

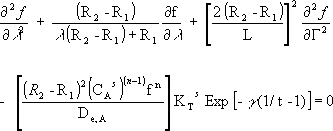(5)

where γ = E_a / R T^s. The boundary conditions are transformed to:

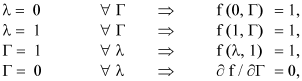
And the new energy balance equation is

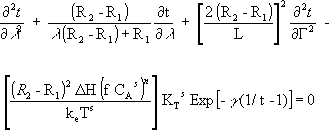(6)

with its boundary conditions:

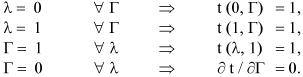
The differential equations for the solid cylindrical pellet case, as much in real as in dimensionless variables, are the same Eqns. 3 to 6, the only changes required are in the boundary conditions for r = 0. In this case, R₁ equals to zero in all expressions and therefore λ= 0. On the other hand, the suppositions listed for the hollow case are held.

In case of solid cylindrical particles, the boundary condition in r = 0 (λ= 0), are:

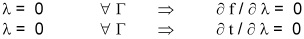
Effectiveness Factor

The effectiveness factor calculation is made by means of definition given in Eqn. 1: "the actual amount of substance that reacts in the whole particle" (numerator) was calculated by summation of all contributions to the reaction at each volume differential element, taking the average concentration and with evaluation of velocity of reaction at the average temperature of each element.

The volume of i-th differential element (numbered consecutively from center to outside) is given by:

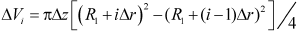(7)

And in dimensionless variables:

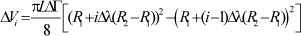(8)

Then the amount of component A reacting in that i-th volume differential element is:

(9)

and the expression for effectiveness factor can be written as the relation between summation of contributions to the chemical reaction at each partition and the reaction evaluated with external surface temperature (T^S) and concentration (C_A^S)

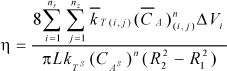(10)

where n_r and n_Z are the number of volume differential elements considered in axial and radial directions respectively.

III. SOLUTION OF MATHEMATICAL MODEL

The effectiveness factor calculation implies the simultaneous solution of differential Eqns. 5 and 6. In this work, the partial differential equations system was discretized by central finite differences and the resulting system of algebraic equations is solved simultaneously (due to the completely implicit formulation) by means of a computer program in an electronic sheet (Excel^™).

Considering the central finite differences equations and the expressions in dimensionless variables (Eqns. 5 and 6), the following expressions for each node of a mesh that divides the catalytic particle can be obtained (after some algebraic arrangement)

Equations for internal and external nodes (0 < λ ≤ 1; 0 ≤ Γ≤ 1)

• Mass balance

(11)

• Energy balance

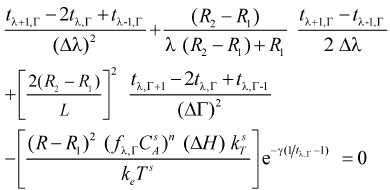(12)

At center of the particles λ = 0 and a mathematical indetermination occurs in the finite differences equations which can be solved by using the L'Hopital's rule

Equations for nodes at the dimensionless longitudinal axis (λ = 0, Γ ≠ 0)

• Mass balance

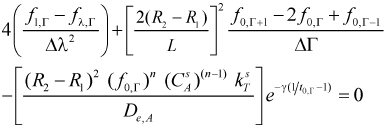(13)

• Energy balance

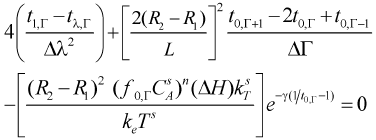(14)

IV. ALGORITHM OF SOLUTION AND DESCRIPTION OF COMPUTER PROGRAM

To solve the mathematical model and for its implementation in the electronic sheet, a quarter of catalytic particle was considered, which was in turn divided by a mesh of 100 nodes (Δ λ = Δ Γ = 0.1)

Because the system of equations is highly non- linear, the velocity of convergence can be low, and to find or not a solution depends on high degree on values with which the dimensionless variables are initialized; After some preliminary tests, the initial value for dimensionless concentrations matrix (If) was taken as zero for all nodes (If₀ =0.0). The dimensionless temperature matrix (It) was initialized as unit for all nodes (It₀ = 1.0), with these values a high stability and velocity of convergence was obtained.

The algebraic relations for the nodes, obtained from the finite differences formulation, were written in the target temperature and concentration matrix (Ot and Of respectively).

Lastly, the mathematical model was programmed for simultaneous calculation of values of matrix If and It making the coefficients of matrix Of and Ot satisfying the differential equations.

In Fig. 2 are shown the concentration and temperature profiles for a solid cylindrical particle in which a first order reaction takes place. The calculated effectiveness factor for this case was 1.215. This results differs from that obtained with the typical calculation with diffusion in radial direction only (Fig. 3), which produces an effectiveness factor of 1.447 (19% higher), and the procedure outlined in this work shows that in the center of the particles the concentration is 20.66% higher and the temperature is 1.31% lesser than that obtained with calculating diffusion in radial direction only.

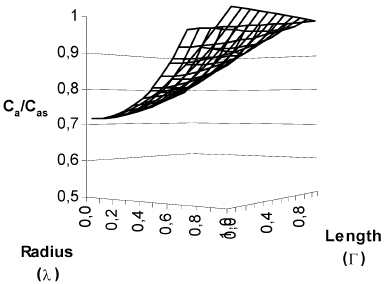
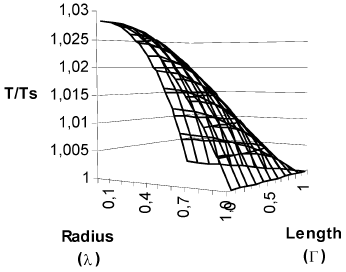
Fig. 2. Concentration and temperature profiles for a finite solid cylindrical catalyst. First order kinetics. β =0.1. γ = 30. C_as = 3.65*10^-7 mol/cm³. T _S = 623 K. R₂ = 0.5 cm. L =1 cm. Φ=1. η = 1.215

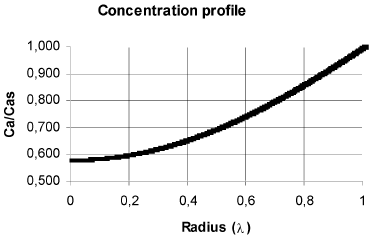
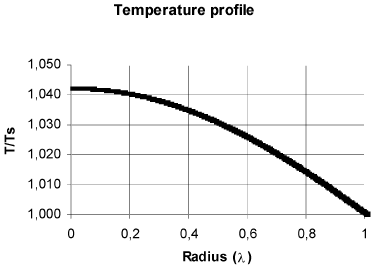
Fig. 3. Concentration and temperature profiles considering radial diffusion only. The geometric, kinetics and properties are the same of Fig. 2. η = 1.447

By way of results validation, in Table 1 the reported data for Davis (1990) (calculated with the computer program DISPL) and that obtained with the algorithm introduced in this work are shown for a dimensionless length Γ = 0.25 and the same conditions reported for Fig. 2. The agreement of results obtained with those programs is excellent.

Table 1. Concentration profiles from Davis and calculated in this work for a finite solid cylindrical catalyst. First order kinetics. β =0.1. γ = 30. L/D = 1. Φ=1. Γ = 0.25.

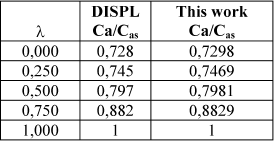
Figure 4 corresponds to temperature and concentration profiles in a hollow cylindrical particle in which a second order reaction takes place. The effectiveness factor of 18.81 is a clear consequence of heat transfer effects inside the particle.

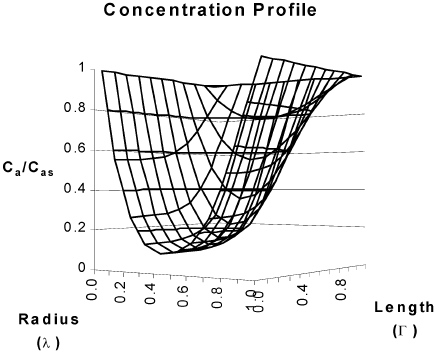
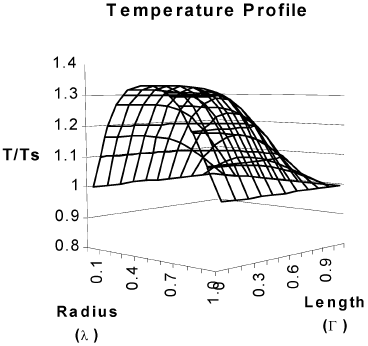
Fig. 4. Concentration and temperature profiles for a hollow cylindrical catalyst. Second order kinetics. β = 0.37, γ = 29.86. C_as = 3.65*10^-7 mol/cm³. T _S = 623 K. R₂=0.5 cm, R₁=0.1 cm L =1 cm , η =18.81

V. CONCLUSIONS

The computer program developed is a robust tool to analyze the efficiency of utilization of cylindrical catalysts. On the other hand, the design of this algorithm, taking into account the diffusion in two directions, allows a clearer appreciation (compared with the calculation of diffusion in only one direction) of effects that the diffusion and heat transfer produces inside cylindrical catalysts.

The proposed algorithm constitutes a flexible tool for the effectiveness factor calculation, additionally, this algorithm can be easily extended to other kinetic expressions, and can be used to optimize the geometric parameters of catalytic pellets, which will be the main objective of the future work.

Finally, it should be highlighted that the numeric strategy becomes very stable, safe in convergence and of high velocity

NOMENCLATURE

C = Concentration
D = Diffusivity.
E_a = Energy of activation of reaction.
f = Dimensionless Concentration.
ΔH = Enthalpy of reaction.
I = Initiation Matrix.
K_T = Reaction velocity constant evaluated at temperature T.
K_e = Effective conductivity.
L = catalyst length.
r = Radial direction
R₁, R₂ = Interior and exterior radius of cylindrical particle.
t = Dimensionless Temperature.
R = Universal constant of gases.
T = Temperature
V = Volume
z = Longitudinal Direction.

Greek letters

β = Physical-chemical Parameter [=ΔH D_e C_A^S/( K_e T^S)]
η = Effectiveness Factor
λ = Dimensionless radial Direction.
γ = Dimensionless longitudinal direction
Γ = Energy of activation parameter
Φ = Thiele's modulus [= R*( K_e / D_e )^0.5]

Sub/superscripts

A = Component in the reaction
e = Effective.
n = Order of reaction
n_r = Number of elements in radial direction
n_z = number of elements in longitudinal direction.
Ο = Initial.
S = Surface.

REFERENCES
1. Carberry, J. J. "The Catalytic Effectiveness Factor Under Nonisothermal Conditions". AIChE J. 7, 350-351 (1961).         [ Links ]
2. Carberry, J. J. Chemical and Catalytic Reaction Engineering. Mc Graw-Hill. New York (1976).         [ Links ]
3. Davis, E. M. Métodos y Modelos Numéricos para Ingenieros Químicos. Compañía Editorial Continental S.A. de C.V. México (1990).         [ Links ]
4. Doraiswamy, L. K. and M. M. Sharma, Heterogeneous Reactions: Analysis, Examples and Reactor Design. Vol. 1. John Wiley and Sons. New York (1984).         [ Links ]
5. Krasuk, J. H. and J. M. Smith, "Effectiveness Factors with Surface Diffusion". Ind. Eng. Chem. Fundam. 4, 102-106 (1965).         [ Links ]
6. Lee, H. H. "Effectiveness Factors for solid-Catalyzed Gas-Solid Reactions". Chem. Eng. Sci. 34, 5-9 (1979).         [ Links ]
7. Lin, Z., N. Shao and T. Li, "Calculation of the Effectiveness Factor of a Spherical Catalyst Using Weighted Residuals". International Chem. Eng. 26, 335 - 339 (1986).         [ Links ]
8. Morbidelli, M.; A. Servida, and A. Varma, "Optimal Catalysts Activity Profiles in Pellets. Part I". Ind. Eng. Chem. Fundam. 21, 278-284 (1982a).         [ Links ]
9. Morbidelli, M.; A. Servida, and A. Varma, "Optimal Catalysts Activity Profiles in Pellets. Part II". Ind. Eng. Chem. Fundam. 21, 284-289 (1982b).         [ Links ]
10. Morbidelli, M. and A. Varma, "Isothermal Diffusion - Reaction in a Slab Catalyst with Bimolecular Langmuir-Hinshelwood Kinetics". Chem. Eng. Sci. 38, 289-296 (1983).         [ Links ]
11. Rusic, D. and S. Zrncevic, "Impurity Poisoning of Ni-Catalysts Pellets". In Catalysts Deactivation. Delmond B. and Froment G. (editors). 623-627 (1994).         [ Links ]
12. Satterfield, C. N. Heterogeneous Catalysts in Industrial Practice. 2 ed. Mc Graw- Hill. New York (1991).         [ Links ]
13. Satterfield, C. N. and T. K. Sherwood, The Role of Diffusion in Catalysis. Addison-Wesley. Massachussets (1963).         [ Links ]
14. Scott, S. K.; T. Boddington, and P. Gray. "Analytical Expressions for Effectiveness Factors in Non-isothermal Spherical Catalysts". Chem. Eng. Sci. 39, 1079-1085 (1984).         [ Links ]
15. Singh, C. P. "A Generalized Method for Calculating Effectiveness Factor". Chem. Eng. Sci. 40, 2375-2378 (1985).         [ Links ]
16. Smith, J. M. Chemical Engineering Kinetics. Mc Graw-Hill. New York (1956).         [ Links ]
17. Trotta, A. and S. Guidice, "Finite Element Solution of Simultaneous Convection, Diffusion and Reaction on Catalytic Surfaces". Computers and Chem. Eng. 9, 167-173 (1985).         [ Links ]
18. Wakao, N., S. Kaguei, and H. Nagai, "Effective Diffusion Coefficients for Fluid Species Reacting with First Order Kinetics in Packed Bed Reactors and Discussion on Evaluation of Catalysts Effectiveness Factors". Chem. Eng. Sci. 33, 183 -187 (1978).         [ Links ]
19. Wang, J. G., Y. W. Li, Y. Chen and S. Y. Peng. "Montecarlo Simulation Effects of Pore Entrance Deactivation on Reaction Performance". Catalysts Deactivation. Delmond B. and Froment G. (editors). 525-530 (1994).         [ Links ]
20. Wohlfahrt, K. "The Design of Catalyst Pellets". Chem. Eng. Sci. 37, 283-290 (1982).         [ Links ]

Received: May 28, 2002.
Accepted for publication: July 8, 2002.
Recommended by Subject Editor Ricardo Gómez.