Some nonlinear mechanical problems solved with analytical solutions

C. P. Filipich^1,2, M. B. Rosales^1,3 and F. Buezas⁴

¹ Department of Engineering, Universidad Nacional del Sur, 8000 Bahía Blanca, Argentina
mrosales@criba.edu.ar
² Mechanical System Analysis Group, FRBB, Universidad Tecnológica Nacional, 8000 Bahía Blanca, Argentina
³ CONICET, Argentina
⁴ Department of Physics, Universidad Nacional del Sur, 8000 Bahía Blanca, Argentina

Abstract — In this paper the analytical solution of nonlinear ordinary differential systems is addressed. Some of the problems are classical in the related literature and exhibit chaotic behavior in certain ranges of the involved parameters despite being simple-looking deterministic systems. The solutions are approached by means of the old technique of power series to solve ordinary differential equations. The independent variable is time in all the illustrations and elementary recurrence algorithms are obtained. This is an alternative to the standard numerical techniques and ensures the theoretical exactness of the response. Several examples are included and trajectories diagrams, phase plots, etc. are shown. The desired numerical precision is attained using time steps several times larger than the usual ones. The availability of an analytical solution may be an additional tool within a standard qualitative analysis. The solution of higher order problems and governed by partial differential equations is under study.

Keywords — ordinary differential equations, nonlinear equations, power series.

I. INTRODUCTION

Power series is an old technique to solve ordinary differential equations (ODE's). A wide open literature is available on the subject. Simmons, 1972, Coddington, 1989, Kreyszig, 1999 may be useful as references in this methodology. The efficiency of this standard technique in solving linear ODE's with variable coefficients is well known. Also an extension known as Frobenious method allows to tackle differential equations with coefficients that are not analytic. Numerical tools such as time integration schemes (e.g. Runge-Kutta, Newmark method, central difference, see for instance Bathe, 1995) are commonly employed to solve nonlinear differential problems. The authors have addressed similar problems with a variational method named WEM (Rosales and Filipich, 2000, 2002). The authors have applied power series numerical tools in various problems (Filipich and Rosales, 2001a, 2002).
   A method to solve nonlinear differential problems governed by ordinary equations (ODEs) is herein employed. The solution is found with an analytical solution using algebraic series. A previous manipulation of the equations leads to very convenient recurrence algorithms which ensure the exactness of the solution as well as the computational efficiency of the method. The approach is straightforward and is illustrated with several problems, i.e. a) projectile motion; b) N bodies with gravitational attraction; c) Lorenz equations; d) Duffing equations and, e) a strong nonlinear oscillator. In all the cases the results are given in plots (state variables vs. time, phase plots, Poincar´e maps). Neither divergence nor numerical damping was found in any case. The availability of an analytical solution may be also a helpful tool in the qualitative analysis of nonlinear equations.
   In this section the general algebra of the approach is stated. The examples will be presented in the following sections Let us consider an analytical function x = x(t) in [0, 1]. We will denote its expansion in power series as (with N → ∞, theoretically)

(1)

and for powers m

(2)

In order to fulfill an algebraic consistence (A.C.) condition the following relationships have to be satisfied

(3)

After replacing the series expressions in each factor of this equation, one obtains the next recurrence formula (Cauchy products)

(4)

or

(5)

Now let us expand an analytical function in Taylor series

(6)

where a_m are known and in particular, we denote

(7)

where a_0k = d_0k are the Kronecker delta's. If we substitute Eq. (2) in Eq. (6) we may write

(8)

in wich

This expression will be used for any analytical function. Now if we have to deal with a rational function

(9)

being and analytical functions and (0) ¹ 0. Also and b_m are known. Then it is possible to write

		(10)

Let us denote

(11)

Now the A.C. must be applied

(12)

(13)

where

The l_k are unknowns and the sets f_k and _k are known. It is apparent that l₀ = ₀/f₀. Then the recurrence relationship for l_k is

(14)

where k = 1, 2, . . . , N. It should be noted that φ0 6= 0 in order for F (0) to exist.
   Equations (4), (5), (14) and similar ones are the basis of this proposal of the analytical solution. That is, the approach is based on the calculation of the series (2) for arbitrary powers of x(t) by systematically stating Cauchy products taken two by two.

II. ILLUSTRATIVE EXAMPLES: Analytical solutions

Five problems will be addressed with this technique: a) projectile motion; b) N bodies with gravitational attraction; c) Lorenz equations; d) Duffing equations and, e) a strongly nonlinear oscillator. The detailed algebra and some numerical examples will be shown in the next five subsections.

A. Projectile motion

Here the problem of the 3D trajectory of a ball fired out in the air (see for instance, Symon, 1979) is tackled by means of the statement of the analytical solution using algebraic recurrence as was shown in the Introduction. The effects of gravity, resistance of the air and wind action are taken into account. The governing equations are

(15)

where x = x(t); y = y(t) and z = z(t). t = t/T is the dimensionless time, [0, 1] . T is an interval of time to be chosen opportunely. is proportional to the air resistance, V_x(z), V_y(z) and V_z(z) represent the wind pressure distribution, and h is the height of the studied domain. The prime denotes the derivative with respect to t . In order to state the algebraic recurrence let us expand the functions x, y, z^m according to the notation (1) with a_1k ≡ A_k, a_1k ≡ B_k and a_mk ≡ C_mk respectively. Similarly we introduce the representation of x', y', z' with a_1k ≡ p_1k, a_1k ≡ q_1k and a_1k ≡ r_1k respectively. The following relationships are true

(16)

The left hand sides of the governing equations are written as

(17)

in which k₀ denotes k = 0 and j_lk ≡ (k+l)!/k!, k and l are integers. It will be necessary to represent the analytical function (z) = e^–z/h in terms of Taylor series (see Eq. (6)) with a_m = (–1/h)^m/m!. Additionally the expression of this function in power series of t is given by

(18)

The functions representing the wind velocity varying with the height are now expanded in Taylor series (Eq. (6)) where , respectively. In turn these functions may be expanded in series of t

(19)

(20)

If we now make use of the A.C. condition ( 3) it is possible to obtain the following recurrence equation

(21)

with m = 2, 3, . . . , M and taken two by two. Let us introduce a simplifying notation

(22)

(23)

After the above definitions and notations we are able to find a recurrence algorithm to solve the differential system (15). First let us write the differential equations in terms of the series

(24)

where the following notation was introduced

The necessary recurrence relationships are given by

(25)

Then the algorithm is complete. Briefly the steps are the following

1. Data and C_0k = 0 are input;

2. Given the initial conditions, C₁₀, A₀, B₀, A₁, B₁ and C₁₁ are found;

3. A value of T is chosen;

4. The calculation is thus performed during a number of steps which depend on the value of T and duration of the experiment;

5. The trajectories x, y and z are finally obtained.

   Figures 1 and 2 show the 3D trajectories for data depicted in Table 1. For both examples M = N = 20, = 0.01, g = 10m/ s², h = 1000m, T = 0.01 s.

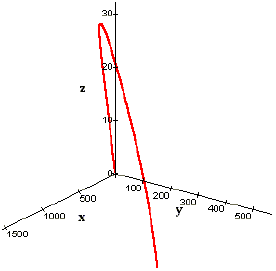
Figure 1: Projectile motion. Example 1.

Figure 2: Projectil motion. Example 2.

B. N-orbiting bodies

The behavior of N bodies attracted to each other in a gravitational force field is tackled by means of the statement of the analytical solution using algebraic recurrence. The forces are assumed varying inversely as the square of the separation among the bodies. Let us define the position vectors of each body in an inertial reference system as

(26)

where i = 1, 2, . . . , NB. NB is the number of bodies. If the non-dimensional time is defined as t = t/T in [0, 1] and T is the interval of interest (parameter to be chosen), the scalar equations of motion may be written

		(27a)
		(27b)
		(27c)

G ≡ T²G^*, G^* = 6.67 10¹¹ Nm²/kg² is the gravitational constant and m_i are the masses of each body. The prime denotes derivative w.r.t. t . Additionally the following notation was introduced

in which conventionally j > i and is the relative position vector.
To obtain the algebraic recurrence let us expand functions x_i, y_i, z_i according to notation (1) with a_1k ≡ A_ik, a_1k ≡ B_ik and a_1k ≡ C_ik respectively and i = 1, 2, . . . , N B. Similarly we introduce the representation of x², y², z², from (2), as a_2k ≡ aik, a_2k ≡ b_ik and a_2k ≡ c_ik , respectively. Other series of type (1) are also necessary: x_ix_j, y_iy_j, z_iz_j, R_ij, and 1/R³_ij represented with coefficients s_ijk.
    The following A.C. conditions applied to the function x, are true

(28)

Analogously with functions y_i and z_i. Other A.C. conditions must be satisfied

		(29a)
		(29b)

   For the sake of brevity the recurrence expression for all the coefficients introduced above are not included. They are derived from the A.C. conditions resulting in equations of the type ( 4) or ( 5). Finally the solving equations are

		(30a)
		(30b)
		(30c)

in which k = 0, 1, 2, . . . , N – 2. The next definitions were introduced

		(31a)
		(31b)
		(31c)

   The necessary steps to find the solution are the following

1. A value of T is chosen;

2. Given the initial conditions, i.e. (0) (position) and (0) (velocity) the values of A_i0, B_i0, C_i0, A_i1, B_i1 and C_i1 are known;

3. The calculation is thus performed using Eqs. (30) and (31) during a number of steps which depend on the value of T and the duration of the experiment;

4. The position (t) and velocity (t) are finally obtained for each body (i = 1, 2, . . . , N B).

The case of four bodies (N B = 4) was numerically solved. Figure 3 shows the relative position among four bodies of masses m₁ = 1, m₂ = 1, m₃ = 5 and m₄ = 1, respectively. The spheres denote the initial position of the bodies, which along with the velocities are given in Table 2. The experiment was run during 750000 s taking 5000 steps of T = 150 s each. See also Filipich et al. 2001b.

Figure 3: Example of four orbiting bodies.

Table 2: N orbiting bodies example. Data.

C. Lorenz equations

Lorenz (see for instance Strogatz, 1994) discovered in 1963 the chaotic motions of a model of convection rolls in the atmosphere. The behavior of this problem is such that very small changes in the initial conditions lead to different solutions, but as Lorenz showed, bounded in a three dimensional butterfly-shaped domain. Here the power series are used to solve the following system of differential equations

(32)

where s^*, r^*, b^* > 0 are parameters; u = û(t); v = . After introducing the variable t = t/T , the following series are adopted

(33)

After the replacement of the series in the differential system the recurrence system is obtained

(34)

where and the Cauchy products are

   Numerical results were obtained with initial conditions u₀ = 0, v₀ = 1, w₀ = 0, T = 0.1, s^* = 10, r^* = 28, b^* = 8/3. N = 20. The time trajectory is shown in Fig. 4 and the phase plane in Fig. 5. The well-known strange attractor is reproduced without numerical perturbation. Being very sensitive to initial conditions these problems pose a challenge to any numerical tool.

Figure 4: Lorenz attractor. Time trajectory

Figure 5: Lorenz strange attractor.

D. Forced Duffing equation

The well-known nonlinear equation extensively known as Duffing oscillator is governed by (see for instance Thompson and Stewart, 1986):

(35)

It is a helpful low-dimensional mathematical model to understand the behavior of more complex dynamic systems. In mechanical engineering this equation may model the response of a forced beam with large deflections. Ueda (1980) identified the chaotic behavior of the response for certain range of the parameters. In this equation u = û(t). After non-dimensionalization the equation reads

(36)

in which p = Tp^*; q = T²q^*; B = T²B^*; V₀ = TV^*₀ and v' = dv/dt . Now let us apply expansions (1) to v and (2) to v³ and (6)) and (8)) to the driving force f (t). Also the derivatives of v may be written as

		(37)
		(38)

and finally the differential equation is transformed into

(39)

A recurrence relationship may be found by stating the A.C. It is possible to find all the values of the coefficients a_mi starting from the initial condition. That is, from Eq. (4) or (5)

(40)

Then from Eq. (39) and since a₁₀ = U₀ and a₁₁ = V₀ the following recurrence expression is obtained

(41)

An illustrative example was numerically solved with the following data: U₀ = 3, V^*₀ = 4, p^* = 0.05, q^* = 1, f(t) = cos(wtT ), B^* = 7.5, N = 20. The arbitrary time of interest was chosen T = 0.35 s. Fig. 6 depicts the time trajectory and the corresponding phase plot is shown in Fig. 7.
These results are coincident with the ones reported by Thompson and Stewart, 1986. As is known, this problem is extremely sensitive to initial conditions changes. This feature is one possible condition for chaos. Consequently the numerical behavior of the employed methodology is relevant to the reliability of the results.

Figure 6: Forced Duffing equation. Time trayectory.

Figure 7: Forced Duffing equation. Phase plot.

E. STRONGLY NONLINEAR OSCILLATOR

Let us introduce the following differential equation

(42)

This equation is related to rotor dynamics. Mahmoud, 2001 studied it with an extended average theorem algorithm. It may represent the scalar part of a complex equation governing a damped nonlinear system. Examples of this behavior appear also in robots and shells as reported in Mahmoud and Aly, 2000.
   When is not restricted to be a small number this equation represents a strongly nonlinear oscillator. The non-dimensionalized equation is

(43)

where x = x(t), in [0, 1] , t = (t – t₀)/T is the nondimensional time, t₀ is the initial time, T is a time interval to be selected and (·)' = d (·) /dt. The constants in the differential equation (43) are A = (wT)² and B = T. In order to solve the equation by means of the power series, function x and its derivatives are expanded as follows

(44)

The nonlinear terms are tackled similarlyThe successive coefficients of the involved functions are obtained with repeated applications of the basic recurrence

(45)

expressions after imposing the A.C. of the type (3), (4)(5) and (6).
   In order to handle a step-wise algorithm the solution is extended to P steps of length T. Then we define t_p in [0, 1] and p = 1, 2, ... P. The sine function is now expanded as

(46)

where {q_j} and {r_j} are known coefficients of the sine and cosine functions. At this stage the differential equation (43) is written for each step

(47)

The initial conditions in each step give place to the starting values a₁₀ = x_0p and a11 = x'_0p. The algorithm is complete after the necessary A.C. of type (3), (4) and (5).
A numerical example was carried out setting T = 0.125 s, w² = 0.306, = 5, t0 = p, x₀ = –0.5, x'₀ = 0, N = 50. The same example was solved in Mahmoud, 2001 with an averaging method, as an extension to the approach for weakly nonlinear systems. Mahmoud reports the time trajectory in a range [p, 28.14] in which only two waves are observed. His results are close to the numerical solution (Runge-Kutta 4th. order) though a difference is noticeable in the plot despite the short interval depicted. Fig. 8 shows the trajectory found with the above described algebraic recurrence plotted in the time domain [p, 375] .One may infer that the response is quasi-periodic given the modulation of the curve.

Figure 8: Trajectory x(t).

In Fig. 9 the same trajectory is plotted in a smaller range together with a numerical solution found using the integration scheme known as forward Euler, implemented in the software MAPLE V as the default algorithm to solve differential equations. The second solution starts to diverge before the 30 s. The corresponding phase diagram is depicted in Fig. 10.

Figure 9: Algebraic series solution (thick line). Numerical solution (forward Euler) (thin line).

Figure 10: Phase diagram. Time of experiment: 375 sec.

In order to have more elements to confirm the supposedly quasiperiodic behavior, a Poincare map is plotted in Fig. 11. It was found for 750 s of duration of the experiment and a sampling time of p. A diamond shaped array of points is observed. Although it might seem that for a longer time of experiment the points would fill the curve (feature of a quasiperiodic response), this is not the case since after a transient behavior the system settles down to a fixed finite number of points which corresponds to a periodic response of several periods.

Figure 11: Poincar´e map. Time of experiment: 750 sec. Sampling time π, 240 points.

F. CONCLUSIONS

A methodology to find the analytical solution of nonlinear differential equations has been presented. The technique makes use of the well-known power series with a systematic handling of nonlinearities and variable coefficients. In order to find the arbitrary powers of the time functions, the Cauchy products are taken two by two. The differential equation is satisfied in each step unlike other numerical schemes which make use of truncated series. The convergence of the method allows to extend the duration of the numerical experiments making possible a long time analysis of the response. Other numerical techniques may show divergence at early stages of the time domain.
   Several examples are derived in detail. The wellknown forced Duffing equation and the Lorenz attractor are solved. Also, the illustrations include the motion of a projectile including the air resistance and the wind pressure, and the orbiting of N bodies under the action of forces inversely proportional to the square of the distance among them. Finally the equation governing a strongly nonlinear oscillator was tackled with the methodology.
    The answer is, in all cases, given by a power series with known coefficients. Then the user may have not only the numerical result but the "analytical" expression of the solution.
    Although this power series technique is very old, the availability of symbolic algebraic manipulation packages might facilitate the systematization of its application.

ACKNOWLEDGMENTS

This work has been partially supported by a PGI grant from SGCyT of the Universidad Nacional del Sur, Argentina. The authors are grateful to the reviewers for their valuable suggestions and contribution to the enhacement of this paper.

REFERENCES

1. Bathe, K-J., Finite Element Procedures, Ed. Prentice-Hall.(1995).
2. Coddington, E.A., An Introduction to Ordinary Differential Equations, New York. Dover Publications (1989).
3. Filipich C.P. and M.B. Rosales, "Analytical solution for some problems with chaotic response", 16th. Brazilian Congr. on Mech. Eng. (COBEM 2001), Uberlandia, Brazil (2001a).
4. Filipich C.P., M.B. Rosales and F. Buezas, "Analytical solutions for ordinary differential equations", Proc. XII Congr Num. Meth. and Appl., Córdoba, Argentina (2001b) (in Spanish).
5. Filipich C.P. and M.B. Rosales, "A Recurrence Solution of Strongly Non-Linear Dynamical Systems", XXI Southeastern Conf. Theor. and Appl. Mech., Orlando, U.S.A. (2002)
6. Kreyszig, E., Advanced Engineering Mathematics, New York. John Wiley & Sons Ltd. (1999).
7. Mahmoud, G.M. and S.A. Aly, "Periodic Attractors of Complex Damped Non-Linear Systems," Int. J. Non-Linear Mech., 35, 309-323 (2000).
8. Mahmoud, G.M., "A theorem for n-dimensional strongly non-linear systems," Int. J. Non-Linear Mech., 36, 1013-1018 (2001).
9. Rosales, M.B. and C.P. Filipich, "An Alternative Technique for Time Integration of Dynamic Equations", Proc. XXIX Jorn. Sudam. Ing. Estr. Punta del Este, Uruguay (2000).
10. Rosales, M.B. and C.P. Filipich, "Time Integration of Non-Linear Dynamic Equations by means of a Direct Variational Method", J.SoundVibr. 254, 763-775 (2002).
11. Strogatz, S.H., Nonlinear Dynamics and Chaos, Ed. Addison-Wesley Pub.Co., Reading, Massachusetts, U.S.A., (1994).
12. Simmons, G.F., "Differential Equations with Applications and Historical Notes". New York. McGraw-Hill (1972).
13. Symon, K.R., Mecanica. Ed. Aguilar (1979).
14. Thompson, J.M.T. and H.B. Stewart, Nonlinear Dynamic and Chaos, Ed. John Wiley & Sons Ltd. (1986).
15. Ueda Y., "Steady motions exhibited by Duffing's equation: a picture book of regular and chaotic motions", in New Approaches to Nonlinear Problems in Dynamics, P.J. Holmes (ed.), 311-322. SIAM: Philadelphia (1980). 109        [ Links ]         [ Links ]         [ Links ]         [ Links ]         [ Links ]         [ Links ]         [ Links ]         [ Links ]         [ Links ]         [ Links ]         [ Links ]         [ Links ]         [ Links ]         [ Links ]         [ Links ]

Received: April 15, 2002.
Accepted for publication: August 7, 2003.
Recommended by Subject Editor Eduardo Dvorkin.