A hybrid neural model for the production of sorbitol and gluconic acid using immobilized Zymomonas mobilis cells

E. F. Fonseca¹, T. L. M. Alves¹, E. L. Lima¹ and M. B. De Souza Jr.²

¹ PEQ/COPPE, Federal University of Rio de Janeiro, Rio de Janeiro - RJ - Brazil
² School of Chemistry, Federal University of Rio de Janeiro, UFRJ - CT, Ilha do Fundão, Bloco E - CP 68542,
21949-900, Rio de Janeiro - RJ - Brazil, mbsj@eq.ufrj.br

Abstract — Only ten years were enough for hybrid neural network-first principle models (HNM) reach a status of a standard industrial tool. This modeling strategy is employed here to represent the production of sorbitol and gluconic acid from glucose and fructose, using permeabilized and immobilized Zymomonas mobilis cells. Mass component balances are derived for the substrate concentrations. A multilayered neural network is used to represent the reaction rate. Experimental results were used to develop and validate the model. The HNM allows the elucidation of the phenomena involved in the process. It is observed from the results that the resistance for mass transfer from the liquid to the particles is increased at higher substrate concentrations and that the reaction rate depends on the concentrations of substrate and product in the particles. Additionally, it may be stated that the flexibility of the HNM allows the development of a model that would otherwise be difficult, if based solely on phenomenological principles.

Keywords — Hybrid Modeling Methods. Neural Networks. Enzymatic Reaction. Basket Reactor.

I. INTRODUCTION

The limitations of neural networks (e.g. extrapolation difficulties) naturally led to the development of hybrid models in which they were integrated with other knowledge representations of the process.

A decade ago, Psichogios and Ungar (1992) proposed a hybrid neural network-first principle modeling strategy (HNM) by the insertion of neural networks into phenomenological models to represent parameters of difficult description. Since then, this kind of HNM was adopted for several applications, such as:

• bioreactors (Thompson and Kramer, 1994; Schubert et al., 1994; Fu and Baford, 1996; Van Can et al., 1997; Tholodur and Ramirez, 1996; De Azevedo et al., 1997; Costa et al., 1999; Henriques et al., 1999);
• chemical reactors (Martinez and Wilson, 1998; Molga and Cherbanski, 1999);
• polymerization reactors (Vega et al., 1997; Nascimento et al., 1999);
• metallurgic reactors (Reuter et al., 1993);
• dryers (Cubillos et al, 1996; Zbicinski et al., 1996; Mateo et al., 1999);
• flotation plants (Cubillos and Lima, 1997; Gupta et al., 1999);
• pressure vessels (Van Can et al., 1996);
• distillation column (Safavi et al., 1999) etc.

Nowadays, the hybrid neural strategy has evolved into a standard industrial technique (Mogk et al., 2002).

In the present work, modeling is used to aid in the development of a new process: the enzymatic production of sorbitol and gluconic acid using permeabilized and immobilized cells of Zymomonas mobilis in a spinning basket reactor.

The objective is that the model helps in the understanding of the phenomena that happen in the process and also provides inferences of variables in the particles of immobilized cells.

With that purpose, a hybrid model is introduced here. This model explicitly considers mass transfer of the substrate from the liquid medium to the immobilized cells as well as the reaction rates, under different operational conditions.

It is expected that the resulting model will allow the optimization of the process.

II. METHODS

A. Zymomonas mobilis

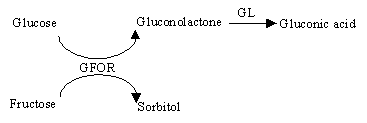
The enzymatic mechanism for Zymomonas mobilis is sketched above. The enzymes GFOR (glucose-fructose oxidoreductase) and GL (gluconolactonase) are present in Zymomonas mobilis cells. GFOR is capable of converting glucose and fructose mixtures, oxidizing the first to gluconolactone and simultaneously reducing the second to sorbitol. GL converts the gluconolactone produced to gluconic acid.

Microorganism and Growth Conditions. The experiments were performed with Zymomonas mobilis CP4 (ATCC 31821), cultivated anaerobically in a medium containing 100 g/L glucose and 5 g/L yeast extract, under controlled temperature of 30 ^oC.

Cell Permeabilization: CTAB (cetyltrime-thylammonium bromide) was added and the cells were agitated during 30 minutes, centrifuged at 5500 rpm during 30 minutes and then washed (Chun and Rogers, 1988). Permeabilization allows the introduction of extrinsic molecules and the release of some compounds, while the enzymes GFOR and GL are retained.

Immobilization: the permeabilized cells were immobilized with κ -carrageenan gel at 4 %. The particles were treated with polyethyleneimine at 1 % (v/v), glutaraldehyde at 0.5 % (v/v) and KCl 0,.3 N (Rehr et al., 1991, Fonseca, 2003). Immobilization was adopted because preliminary investigations indicated that this operation improves the stability of the permeabilized cells (Fonseca, 2003).

B. Experimental Set-up

The reactions with immobilized cells were carried in a 1 L bioreactor, with a 0.5 L working volume, in batch mode. The particles were put in three cylindrical baskets (3 cm diameter, 6 cm height) attached to the stirrer. Temperature was controlled at 39 ^oC. A pHmeter (Chemcadec model 565200), which added a KOH 3N solution to the medium through a peristaltic pump (Masterflex model 77120-60), controlled pH at 5.5. A m_x cell mass was employed (Table 1).

Figure 1 exhibits the experimental apparatus. The electronic balance was interfaced with a computer and sent signals corresponding to the amount of alkali added to the reactorconcentrations to a computer. These signals had to be treated by digital low-pass filters, because high frequency noise was present.

Figure 1: Experimental apparatus.

C. Analytical Methods

Cell concentration was determined by dry weight.

As the enzymatic reaction is equimolar, the concentration of the substrates and products were inferred, during the course of reaction, by on-line monitoring of the alkali, of known concentration, that was added to the medium to neutralize the gluconic acid formed. These inferences were validated by HPLC measurements (Fonseca, 2003).

D. Proposed Model

A model was derived to represent the process. It considers that the substrate in the liquid medium is transferred to the immobilized cell particles, where the reaction happens.

Equation (1) describes the variation of the volume of liquid V that occurs due to the flow rate F of alkali, added to control the pH. Equation (2) models the variation of the number of moles of glucose in the liquid, given by the product GV, where G is the glucose concentration. Equation (3) represents the variation of glucose concentration G_p in the particles, where G’_p is the concentration on the surface of the particles.

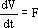	(1)
	(2)
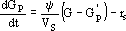	(3)

In these equations

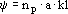
where a is the interfacial particle area; n_p, the number of particles and kl, the mass-transfer coefficient. The mass transfer by diffusion inside the particles is considered very fast, when compared to the reaction rate. Hence, the concentration gradient inside the particles is assumed negligible, so that:

. (4)

Equations (1) and (2) may be combined to give the variation of glucose concentration in the liquid:

. (5)

The fact that the reaction is equimolar is used to calculate the concentrations of the two substrates and two products based on the equations above (written for glucose). For each mole of glucose consumed, one mole of fructose is also consumed and one mole of gluconic acid and one mole of sorbitol are produced.

III. EXPERIMENTAL RESULTS

The four experimental conditions chosen for this study are shown in Table 1. Equimolar initial concentrations of glucose and fructose were employed.

TABLE 1: Experimental Conditions

The number of particles n_p put in the basket was 200. This renders the following volume of solids V_s:

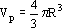	(6)
	(7)

where V_p is the volume of each particle, with radio R = 0.03 dm. The area is a = 2.8 x 10^-3 dm².

The results of four batches runs are shown in Figs. 2, 3 and 4. The experimental points are plotted by the use of symbols. In this paper only model curves are represented by continuous lines.

Figure 2 shows the volume variation for each experiment. The flow of alkali to the reactor is not continuous, due to the on-off nature of the pHmeter. In order to facilitate the development of the simulations, polynomial approximations were obtained for the flow in each case. Quadratic equations in the form of Equation (8) were developed for each experiment.

F = f₀ + f₁ t + f₂ t² (8)

Table 2 gives the coefficients of Equation (8) for each experiment.

TABLE 2: Parameters of the Polynomial Fit for the Flow

Figures 3 and 4 show the transient behavior for the glucose and sorbitol concentrations for the four batches.

Figure 2: Medium volume increase.

Figure 3: Temporal profile of glucose concentration.

Figure 4: Temporal profile of sorbitol concentration.

IV. HYBRID NEURAL MODEL

A. Development of the model

In the usual HNM strategy, a neural network is used to represent the reaction rate. The mass balance equation is then rewritten in order to put the reaction part in terms of other known factors, as follows:

Reaction rate = accumulation + transport rate (9)

So an approximation for the derivative (accumulation) term is necessary. It is possible to use polynomial approximation to fit the curves and then calculate the derivative of the polynomials. However, this strategy may lead to oscillation of the fitted curve.

An alternative strategy was adopted here. It was considered that the curves for glucose moles (GV) exhibit a similar behavior to the step response of a critically damped (damping factor, ζ = 1) second order with zero process, given by (Seborg et al., 1989):

(10)

where Eq. (10) gives the deviation from the initial value of GV and τ , τ _a and k are parameters of the model (Seborg et al., 1989). Under this assumption, Eq. (10) was used to adjust the experimental data instead of a polynomial one.

Non linear regression (Quasi-Newton) was applied The parameters of Eqn.Eq. (10) were obtained, as Table 3 summarizes, with coefficients of determination R² approximately equal to 1. Figure 5 shows that the curves fit exactly the experimental data.

TABLE 3: Parameters of Eq. (10)

Figure 5: Fit of GV curves using temporal linear models.

Other difficulties arise when trying to solve equations (1) to (3). As it is assumed that the reaction happens in the particles and only bulk concentrations are measured (that is, G_P is not measured), the accumulation term in Eqn.Eq. (9) is not known (dGp/dt).

In the following, the manipulations necessary to obtain the reaction rate in terms of known variables are presented.

First, an expression for G_P in terms of kl is obtained from equation (2):

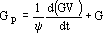(11)

where G is known and the first derivative of GV may be obtained by taking the first derivative of equation (10):

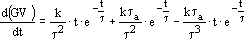(12)

Now, derivingif Eqn.Eq. (2) and using Eq. (4) and Eq. (3),is derived, subsequently, to substitute respectively and 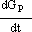, the following equation is obtained:

(13)

An expression for the reaction rate may be obttained from the previous equation:

(14)

where G is known, G_p is given by equation (11) and the second derivative of GV may be calculated from Eq. (10):

(15)

Based on experimental evidences that kl depended both on ϖ and G, a variable representation for the mass transfer coefficient was assumed:

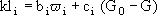(16)

where b_i and c_i are constants for each experiment.

The derivative of ψ is then given by:

. (17)

Equation (14) -together with Eqs. (11), (15) and (17)- provides a way to calculate the reaction rate. These values will be necessary to obtain the kinetic description of the process as presented in next item.

B. Training of the net

A multilayered neural network was trained to represent the reaction rate.

After some preliminary tests, a configuration was chosen in which the inputs consisted of concentration of glucose in the particles, initial concentration of glucose in the medium and concentration of sorbitol (G_p; G₀ and P, respectively). The output corresponded to the specific reaction rate ν ., being the target values obtained from Eq. (14).

The data for training and validation were taken from the experimental batches, consisting of 1106 patterns. Aditionally, 100 patterns were built in order to show to the net that the reaction rate was null if G_p = 0. Two thirds of the resulting patterns were randomly selected for training and one third for validation.

Figure 6: Trained multilayer neural net.

The STATISTICA^™ Neural network module was used in order to select the nets. The chosen one is shown in Figure 6. A total of 7 hidden hyperbolic neurons was used. The output neuron was sigmoidal.

In the training, a total of 100 epochs was carried using backpropagation and 19 epochs using conjugate gradient. The correlation coefficient between the predicted and observed data was 0.999.

V. RESULTS

The hybrid model given by Eqsn. (1) to (3) - with the neural net describing the reaction rate - was used to simulate the batch experiments. A Nnumerical solvers from MATLAB^™ (ode15s) wasere used to integrate the equations were from the initial values for G (experimental) and G_P (G_P(0)=0). It must be emphasized that these two data are the only ones necessary to run the model.

Figure 7 shows the experimental curves and the results of the HNM. A good agreement is observed for the four experiments, showing that the model was able to generalize from the presented data.

The model also provides profiles for G_P, a variable that is not measured. It can be seen in Figure 8 that the G_P and G curves are more detached when the initial concentration of glucose in the medium is higher. It can also be noticed that the concentration gradients last longer in the experiment with the highest initial concentration of substrate (Exp. 4).

Figure 7: Results of the HNM model.

The values assumed for the mass transfer coefficient depend on the agitation speedagitation frequency of the stirrer and on the glucose molar concentration, being empirically adjusted by the linear multiple model given by Eqn.Eq. (16).

Table 4 presents the parameters of Eq.(16). These parameters were calculated in order to satisfy the condition that, in t = 0, both glucose concentration and specific reaction rate in the particles must equal zero.

The conditions were chosen so that higher agitation frequenciesspeeds were imposed (ω₁ = 180; ω₂ = 200 and ω₃ = 210 rpm) at higher initial substrate concentrations. These operational procedures took into account the fact that, with low concentrations, a high agitation frequencyspeed could disrupt the particles of the immobilized cells.

Figure 8: Results of the HNM model.

TABLE 4: Parameters of the Mass Transfer Coefficient Equation

VI. CONCLUSIONS

A new process is being presently developed using immobilized Zymomonas mobilis cells to produce sorbitol and gluconic acid from glucose and frutose.

A model was introduced here which include mass transfer and reaction terms. The problem of deriving a model for this process is difficult because the reaction happens in the particles.

A hybrid phenomenological-neural model was developed. Specifically, the neural network describes the kinetic terms. As the diffusion in the particles was not explicitly taken into account, it can be considered that the neural network models an apparent (nor intrinsic) kinetic rate in the particles.

It was shown that the HNM fits the experimental data used in the development and was able to generalize from the training data. The model also provides inferences of variables that are not actually measured (G_P) and allows the verification of the importance of a mass transfer coefficient for higher substrate concentrations.

Additionally, the use of linear temporal auxiliary equations to describe the profiles of the variables appears as an interesting alternative, as they do not oscillate (as polynomial equations may) and are easily differentiated. The application of these equations to calculate the derivatives needed by the HNM approach is innovative, to the knowledge of the authors.

REFERENCES
1. Chun, U.H. and P.L. Rogers, "The simultaneous production of sorbitol from fructose and gluconic acid from glucose using oxidoreductase of Zymomonas mobilis", Appl. Microbiol. Biotechnol., 29, 19-24 (1988).         [ Links ]
2. Costa, A.C., A.W.S. Henriques, T.L.M. Alves, R. Maciel Filho and E.L. Lima, "A hybrid neural model for the optimization of fed-batch fermentations", Brazilian Journal of Chem. Engng., 16, 1, 53-63 (1999).         [ Links ]
3. Cubillos, F.A., P.I. Alvarez, J.C. Pinto and E.L. Lima, "Hybrid-neural modeling for particulate solid drying process", Powder Technol., 87, 153-160 (1996).         [ Links ]
4. Cubillos, F.A. and E.L. Lima, "Identification and optimizing control of a rougher flotation circuit using an adaptable hybrid-neural model", Minerals Engng., 10, 7, 707-721 (1997).         [ Links ]
5. De azevedo, S.F., B. Dahm and F.R. Oliveira, "Hybrid modelling of biochemical processes: a comparison with the conventional approach", Comp. Chem. Engng., 21, Suppl., S751-S756 (1997).         [ Links ]
6. Fonseca, E.F., "Estudo da produção de sorbitol e ácido glicônico por células permeabilizadas e imobilizadas de Zymomonas mobilis em reator tipo cesta agitada", D.Sc. Thesis, PEQ/COPPE/UFRJ (2003).         [ Links ]
7. Fu, P.-C. and Barford, J.P., "A hybrid neural network - first principles approach for modelling of cell metabolism", Comp. Chem. Engng., 20, 6/7, 951-958 (1996).         [ Links ]
8. Gupta, S., P-H. Liu, S.A. Svoronos, R. Sharma, N. A. Abdel-Khalek, Y. Cheng and H. El-Shall, "Hybrid first-principles/neural networks model for column flotation", AIChE Journal, 45, 3, 557-566 (1999).         [ Links ]
9. Henriques, A.W.S., A.C. Costa, T.L.M. Alves and E.L. Lima, "A hybrid neural model of ethanol production by Zymomonas mobilis", Applied Biochem. Biotechnol., 77-79, 277-291 (1999).         [ Links ]
10. Martinez, E.C. and J.A. Wilson, "A hybrid neural network-first principles approach to batch unit optimisation", Comp. Chem. Engng., 22, Suppl., S893-S896 (1998).         [ Links ]
11. Mateo, J.M., F.A. Cubillos and P.I. Alvarez, "Hybrid neural approaches for modelling drying processes for particulate solids", Drying Technol., 17 (4-5), 809-823 (1999).         [ Links ]
12. Mogk, G., T. Mrziglod and A. Schuppert, "Application of Hybrid Models in Chemical Industry", Proceedings of the European Symposium on Computer Aided Process Engineering - 12, 931-936 (2002).         [ Links ]
13. Molga, E. and R. Cherbanski, "Hybrid first-principle-neural-network approach to modelling of the liquid-liquid reacting system", Chem. Engng. Science, 54, 2467-2473 (1999).         [ Links ]
14. Nascimento, C.A.O., R. Giudici and N. Scherbakoff; "Modeling of industrial nylon-6,6 polymerization process in a twin-screw extruder reactor. II. Neural networks and hybrid models", Journal of App. Polymer Science, 72, n.7, 905-912 (1999).         [ Links ]
15. Psichogios, D.C. and L.H. Ungar, "A hybrid neural network - first principles approach to process modeling", AIChE Journal, 1499-1512 (1992).         [ Links ]
16. Rehr, B., C. Wilhelm and H. Sahm, "Production of sorbitol and gluconic acid by permeabilized cells of Zymomonas mobilis", Appl. Microbiol. Biotechnol., 35, 144-148 (1991).         [ Links ]
17. Reuter, M.; J.S.J.V. Deventer and T.J.V.D Walt, "A generalized neural-net kinetic rate equation", Chem. Engng. Science, 48, 7, 1281-1291 (1993).         [ Links ]
18. Safavi, A.A., A. Nooraii and J.A. Romagnoli, "A hybrid model formulation for a distillation column and the on-line optimisation study", Journal of Process Control, 9, 125-134 (1999).         [ Links ]
19. Schubert, J., R. Simutis, M. Dors, I. Havlik, A. Lübbert, "Hybrid modelling of yeast production process", Chem. Engng. Technol., 17, 10-20, 1994.         [ Links ]
20. Seborg, D.E., T. F. Edgar and D. A. Mellichamp, "Process Dynamics and Control", John Wiley & Sons, New York (1989).         [ Links ]
21. Tholodur, A. and W.F. Ramirez, "Optimization of fed-batch bioreactors using neural network paramenter function models", Biotechnol. Prog., 12, 302-309 (1996).         [ Links ]
22. Thompson, L.M. and M.A. Kramer, "Modeling chemical processes using prior knowledge and neural networks", AIChE Journal, 40, 8, 1328-1340 (1994).         [ Links ]
23. Van Can, H.J.L., C. Hellinga, K.C.A.M. Luyben, J.J. Heijnen and H.A.B. Braake, "Strategy for dynamic process modeling based on neural networks in macroscopic balances", AIChE Journal, 42, 12, 3403-3418 (1996).         [ Links ]
24. Van Can, H.J.L., H.A.B. Braake, C. Hellinga, K.C.A.M. Luyben, and J.J. Heijnen, "An efficient model development strategy for bioprocesses based on neural networks in macroscopic balances", Biotechnol. and Bioengng., 54, 6, 549-566 (1997).         [ Links ]
25. Vega, M.P., E.L. Lima and J.C. Pinto, "Modeling and control of tubular solution polymerization reactors", Comp. Chem. Engng., 21, Suppl., S1049-S1054 (1997).         [ Links ]
26. Zbicinski, I., P. Strumillo, and W. Kaminski, "Hybrid neural model of thermal drying in a fluidized bed", Comp. Chem. Engng., 20, Suppl., S695-S700 (1996).         [ Links ]