Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.34 n.4 Bahía Blanca oct./dic. 2004
Evaluation of some methods for lower bound determination in the transition region of ferritic steels
C. Berejnoi1, J.E. Perez Ipiña2
1 Fac. de Ingeniería, Univ. Nac. de Salta, 4400 Salta, Argentina
berejnoi@unsa.edu.ar
2 Grupo Mec. de Fractura, Univ. Nac. del Comahue / CONICET, 8300 Neuquén, Argentina
pipina@uncoma.edu.ar
Abstract ¾ Fracture toughness characterization of ferritic steels in the ductile to brittle transition region is problematic due to the observed scatter. This scatter makes not possible to obtain a single toughness value, although some statistical methods presented in the literature allow to manage it and indeed to have a lower bound value.
The ability of some of these proposals to give a technological lower bound value from experimental sets of data was studied. Data from literature and our research were used for this purpose. One hundred random combinations of reduced number of elements from each data set were taken, repeating this procedure for different number of elements. The lower bound value dependence on sample size and the minimum number of specimens needed for a technological lower bound value determination were studied. The SPRÖDZON Method seems to give the best estimation of a technological lower bound LB.
Keywords ¾ Lower Bound. Ductile-To-Brittle Transition. Brittle Fracture. Weibull Statistics.
I. INTRODUCTION
Interpretation of fracture toughness results of welded joints and ferritic steels in the ductile to brittle transition region becomes problematic due to the great scatter observed. This is generally attributed to a probabilistic effect, resulting from the distribution of low toughness triggering points for cleavage initiation in the volume surrounding the crack front. Specimen size plays an important role on the measured fracture toughness becauseit would influence not only the exposed material volume but also different thickness, causing differences in constraint.
The statistical data treatment has been preferably performed by means of Weibull statistics. The two-parameter Weibull was the first distribution used (Landes and Shaffer, 1980), although afterwards the three-parameter Weibull distribution (Landes and McCabe, 1982) was also employed. Kim Wallin (1989a, b) proposed a three-parameter Weibull distribution with fixed threshold and shape parameters, with toughness results corrected both by large-scale plasticity and stable crack growth. In this way, the number of specimens necessary to calculate an acceptable Weibull distribution could be reduced, because only the scale parameter was necessary to be estimated.
The Weibull distribution is often associated to the weakest link model (WLM). However, it is not clear which regime this model would be valid in. Heerens et al. (1993) stated that the WLM is invalid when previous ductile crack growth (DCG) or constraint loss are present, or in cases where there is no evidence of an unique cleavage initiation point. They proposed to split the whole data set into two zones by means of a Border Line. One of these zones corresponds to the tests that satisfy WLM. Landes (1993) explained the nature of the fracture toughness scatter in the transition regime of ferritic steels by means of a two criteria statistical model: the Weibull statistics (associated to the WLM) in the middle temperature range of the transition and a normal statistical distribution (associated to a critical damage accumulation) in the early part of the transition.
Anderson et al. (1994) expressed that the WLM is a necessary but not a sufficient condition for the occurrence of cleavage, and demonstrated that the probability distribution of the WLM corresponds to a two-parameter Weibull distribution (shape parameter equal to 4 when K is used as fracture toughness parameter). According to these authors, in spite of the fact that the three-parameter Weibull distribution describes in a good way the sets of experimental data, it has no theoretical basis. Experimental results had to be corrected for stable crack growth and large scale plasticity. In disagreement with Wallin`s constant value of threshold parameter, they proposed a temperature-dependent threshold equal to the arrest toughness (Kia). Censoring the highest toughness data, or applying different-from-Weibull statistical functions were also proposed (Moskovic, 2002; Heerens et al., 2001).
From a technological point of view, it is very convenient to determine only one value of fracture toughness in order to characterize the toughness of the material for a given temperature. Obviously this must be related to a lower bound (LB) value.
Many proposals for calculating LB of ferritic steels in the transition region can be found in literature. Some of them are:
A. Proposals of Iwadate et al.
Iwadateet al. (1983) proposed that the following relation must be verified to have a valid LB value in a set of N specimens:
 | (1) |
Constant value is 1000 or 3000, depending on the presence or absence, respectively, of ductile crack growth previous to cleavage. It has been shown (Perez Ipiña et al., 1994) that the NB value obtained by using Eqn. (1) does not correspond to the thickness limit given by ASTM.
The minimum toughness value (JCmin) in a set of N specimens is analyzed. If this Jcmin satisfies Eqn. (1), then it is considered as LB. More tests must be performed when the minimum toughness value in the set does not satisfy Eqn. (1).
This proposal considers two situations: temperatures at which stable crack growth precedes brittle fracture, and temperatures at which no stable crack growth is present at the moment of fracture. It is well known that in the ductile to brittle transition region there are temperatures at which some specimens break without any trace of previous ductile crack growth while others show some stable extension of the crack (Perez Ipiña et al., 1994). It is therefore difficult to split sets presenting tests with or without DCG, in order to use different constant values (i.e., 1000 or 3000 when working with integral J).
Later, Iwadate and Yokobori(1994) proposed as LB a fracture toughness value corresponding to 3% failure probability. This value can be obtained by means of a two-parameter Weibull distribution, with both parameters estimated from the experimental data set.
B. Proposal of Landes et al. (1994)
Landes et al. (1994) proposed this method for the determination of a LB value testing only one specimen. They based their method on Iwadate et al.'s proposal (1983), obtaining the minimum number of specimens N as
 | (2) |
where Jfc corresponds to the experimental toughness value, B is specimen thickness and sy is material stress flow.
They also considered a scatter band following a two parameter Weibull distribution with slope m = 2, estimating the cumulative probability as F=i/N+1. They assumed the Jfc value as the upper bound, corresponding then to the position of probability N/(N+1), hence the lower bound, JLB, must have a probability estimated value of 1/(N+1). Then JLB can be calculated as:
 | (3) |
Landes et al. (1994) stated that this method works in a better way for small specimen sizes.
When the analysis is performed by using K data sets, and taking into account the relationship:
 | (4) |
The values of N and m result:
 | (5) |
with K expressed in MPa.m1/2, B in mm and sy in MPa.
Then the LB calculated applying Eqn. (3) corresponds to the minimum toughness value that would be obtained with a set of N specimens if the scatter is described by a two-parameter Weibull distribution with the slope m=2 (4 when the analysis is made with K values).
C. SPRÖDZON Method (Wallin and Hauge, 1992)
This simple method is termed the Sprödzon method from an international cooperative research project with the same name where the method was elaborated. It appears as a promising candidate for implementation in specifications and international standards as a method for characterization of fracture toughness test data (Wallin and Hauge, 1992). The statistical data significance is quantified by means of a fractile and a trust level, being possible to apply the method in any data set size (3 or more specimens), and even to make comparisons between sets of different sizes.
This method makes use of two basic relationships. One is the Binomial Probability for the minimum value in a data set (Fmin). For a selected trust level Fconf and a data set size (N):
 | (6) |
The term Fmin represents the accumulated probability of the minimum toughness value in a data set. The binomial probability does not include any supposition of data statistical distribution.
The second basic relationship is the statistical distribution related to the lower tail of the considered population. Hauge et al. (1994) expressed that if this region is characterized by brittle fracture without previous stable crack growth, it can be described by means of a two-parameter Weibull distribution with slope m = 2 when CTOD is used as fracture toughness parameter.
It is assumed that both Fmin and the minimum CTOD (d) values define one point in the Weibull distribution, i.e., one point in the lower tail of the population. In this way, the scale parameter is implicitly determined and any fractile of the distribution can be calculated. For a specified probability level F, the characteristic CTOD value (dLB) may be obtained as:
 | (7) |
This method was proposed in order to be used only in cases where no previous ductile crack growth was observed (Da= 0), so it should be limited to the lower transition zone. It does not match the two failure mode model proposed by Landes (1993), which states that there is not a valid Weibull distribution but a Normal one in this zone. It is not clear how those sets of data presenting a fraction of specimens that fractured after some stable crack growth must be treated, i.e., whether this model is able to be used, whether the data set must be censored or whether they must be corrected due to DCG effect. Expressing Eqn. (7) in terms of K , it results:
 | (8) |
When J integral is used, d must be replaced by J in Eqn. (7).
D. ASTM E 1921 Standard (1997)
This relatively new ASTM standard uses the Master Curve concept proposed by Wallin (1989b) and requires the use of six or more specimens for fracture toughness characterization of ferritic steels in the ductile to brittle transition. After converting elastic-plastic J toughness parameter to equivalent linear-elastic parameter K and censoring the data that does not fit a size criterion, a three parameter Weibull Distribution (with the slope parameter equal to 4 and threshold parameter equal to 20) is used for the determination of a mean toughness value. Failure probability analysis can then be performed and a LB value could be determined, although the standard gives no orientation to do this.
The main scope in this work was to study the ability of different methods to predict engineering LB values in a simple manner, using experimental data sets without corrections. All the analyzed proposals are in some way based on Weibull statistics; one of them corresponds to the distribution presented by Wallin (1989b), and now used in the ASTM E 1921 standard (1997) for fracture toughness characterization of ferritic steels in the ductile to brittle region. The minimum number of specimens necessary to have an acceptable LB value was also analyzed.
II. MATERIALS AND METHODS
The analyzed methods were:
- Method of Landes et al. (1994), taking for the analysis both the lowest and the highest toughness value in each subdata set.
- SPRÖDZON Method (Wallin and Hauge, 1992)
- Based on the proposal of Iwadate et al. (1994), a failure probability of 3% using different Weibull distributions was considered as LB:
a) two and three-parameter Weibull distributions, estimating the corresponding parameters.
b) Weibull distribution with fixed shape and threshold parameters, estimating only the scale parameter, including the distribution used in the ASTM E 1921 standard (1997) to handle statistic data. Table 1 shows the values of such fixed parameters for the different cases analyzed.
Table 1. Values of shape and threshold parameters when they are considered as fixed (ASTM E 1921)

The data sets used, shown in Table 2, were either our own laboratory results or taken from literature. Only raw data were analyzed, i.e. no corrections for stable crack growth nor for large scale plasticity were considered. The aim was not to deny the influence of such factors on toughness results, but to obtain a technological LB value using simple methodologies.
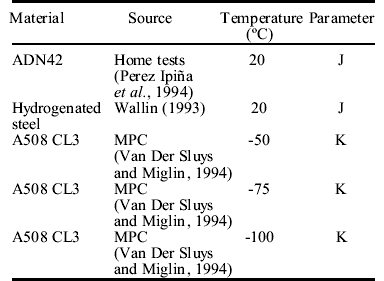
Table 2. Analyzed data sets
In this way, a LB for each combination was obtained for different sample sizes, taking the whole data set as population (N is the population size). This procedure was repeated for each of the methods listed above. In this way, a distribution of LBs for each "sample size" was obtained.
All the samples, those tested by the authors and those taken from the literature, were obtained following standardized procedures.
III. RESULTS
Tables 3 to 7 show LBmean values and standard deviations of the evaluated methods. Each table corresponds to a single material data set, and each row of the table to values obtained from 100 random combinations of n selected from N specimens, beginning in 3 for the first row and increasing by 3 for the following rows until the total number N of specimens or a quantity considered sufficient. The last row shows the LBs for the complete data set (only one combination, therefore null deviation). The minimum number of specimen (Nmin) necessary for a technological lower bound value determination was also intended to be determined in this section. For such determination, the values of LBmean and the scatter band versus the number of specimen were plotted for each data set and each method. Nmin was chosen by the authors as the value of n for which the LBmean becomes approximately constant and the standard deviation is acceptable.
Table 3. ADN42 data set (Perez Ipiña et al., 1994). Jmin= 5.23 KJ/m2. Mean values (  ) and standard deviations (s) of 100 combinations.
) and standard deviations (s) of 100 combinations.
Table 4. Wallin (1993) data set. Jmin= 44 KJ/m2. Mean values ( ) and standard deviations (s) of 100 combinations.
) and standard deviations (s) of 100 combinations.
Table 5. MPC-JSPS (T= -50 oC) (Van Der Sluys and Miglin, 1994) data set. Kmin= 68.2 MPa.m1/2. Mean values ( ) and standard deviations (s) of 100 combinations.
) and standard deviations (s) of 100 combinations.
Table 6. MPC-JSPS (T= -75 oC) (Van Der Sluys and Miglin, 1994) data set. Kmin= 101 MPa.m1/2. Mean values ( ) and standard deviations (s) of 100 combinations.
) and standard deviations (s) of 100 combinations.
Table 7. MPC-JSPS (T= -100 oC) (Van Der Sluys and Miglin, 1994) data set. Kmin= 58.7 MPa.m1/2. Mean values ( ) and standard deviations (s) of 100 combinations.
) and standard deviations (s) of 100 combinations.
Table 8 shows the values of Nmin obtained for the different methodologies applied to the considered data sets. In this table the characteristics of the prediction (presented in the columns named "Pred") are also shown:
VC: very conservative
C : conservative
G: good
BC: barely conservative
NC: non conservative
This graphical analysis was performed in all of the data sets, although only one is shown in the paper. Figures 1 to 6 show the variation of LBmean and the scatter band for one standard deviation with n, for one MPC-JSPS data set (T= -50 oC) and each of the methods analyzed. Figure 6 describes the methodology employed for the determination of Nmin: although LBmean is almost constant for values of n greater or equal to 6, Nmin was considered as being 15 because the great scatter observed for small n. Figures 1 and 2 show that for Landes et al. method a value of Nmin for MPC-JSPS (T= -50oC) is not possible to establish, this was marked with a "?"symbol in Table 8.
Table 8. Nmin values for different methodologies and various data sets.

Fig. 1. MPC-JSPS (T= -50o C) data set. Landes Method (using minimum).

Fig. 2. MPC-JSPS (T= -50oC) data set. Landes Method (using maximum).

Fig. 3. MPC-JSPS (T= -50o C) data set. Sprödzon method.

Fig. 4. MPC-JSPS (T= -50o C) data set. LB as 3% of a two parameter Weibull distribution.
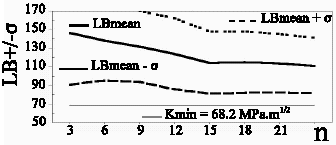
Fig. 5. MPC-JSPS (T= -50o C) data set. LB as 3% of a three parameter Weibull distribution.

Fig. 6. MPC-JSPS (T= -50o C) data set. LB as 3% of a Weibull distribution with fixed parameters.
IV. ANALYSIS
The LBmean values obtained for the 100 combinations for each "n" were not always lower than the experimental minimum, and they showed diverse tendencies depending on the analyzed method and the set of data. Generally the LBmean diminished as the specimen number taken in the analysis was increased. When the number of used specimens was small, the LBmean values were generally higher than the experimental minimum one, while for high "n" the LBmean values, in spite of diminishing, were not always lower than the experimental minimum. In some cases, individual LBs were much higher than the minimum obtained experimentally.
The different methods presented varied tendencies as are commented below:
Landes et al.: although Landes et al. method was proposed to calculate a lower bound using only one fracture toughness result, when fracture mechanics tests are performed in the transition region there are several results, i.e., three or more. In such situation, the method can be applied using the maximum or the minimum experimental J value, resulting in the determination of two different LB values. This method generally showed low scatter using either the minimum or the maximum experimental value of the data subset, although, the values of LB turned out unpredictable: for the minimum values, the calculated LBs were sometimes very conservative and other times not; and for the maximum toughness values, the LBs were sometimes in agreement with the minimum of the whole data set, and were other times non conservative.
SPRÖDZON: this method presented also small Nmin, although not smaller than Landes et al. LBs predicted were much closer to the experimental minimum than Landes et al. prediction.
Two Parameter Weibull: the observed Nmin values were greater than SPRÖDZON and Landes et al., and besides this, the LBs obtained were frequently non conservative.
Three Parameter Weibul: as expected, the Nmin values were higher than the ones obtained by other methods. It also presented many non conservative LBs.
Weibull with Fixed Parameters: although the Nmin were frequently small, the LBs obtained were nearly always non conservative. This would be justified by the fact that this distribution was proposed for corrected data, and in this paper no corrections were applied.
The method that showed the lowest Standard Deviation was that proposed by Landes et al. (1994), although the predicted LB values were not reliable, sometimes too small and in other cases very high (Table 3 to Table 7).
Except for Landes et al. method, all of the analyzed proposals presented high standard deviations in the predicted LBs for small "n". These deviations decreased as "n" increased. As it was expected, as the number of parameters to be estimated in the distribution increased, a larger population size for a good estimation was needed.
The SPRÖDZON method seems to be the best approach for a technological LB estimation:
- in general the LBmean agreed in a good manner with the minimum experimental (Table 3 to Table 7); - it showed an acceptable standard deviation; - the obtained Nmin were among the lowest of all considered methods.
The worst results were obtained when the LB was estimated as a 3% failure probability using the fixed-parameters Weibull distribution. Despite almost constant LBmean values were obtained for "n" higher than 3, their values were generally very high. Except for two data sets, involving the whole data, the calculated LBs were higher than the minimum experimental fracture toughness values. Although a LB value slightly higher than the minimum experimental would be expected when a 3% failure probability is applied over a large number of specimens, in some cases this difference was higher than 100%.
The ASTM standard (ASTM E 1921, 1997), based on the Master Curve Approach proposed by Wallin (1989b), establishes the use of a fixed-parameter Weibull distribution for the statistical characterization of the test results similar to the analyzed here. Six specimens are enough in this standard. As it was mentioned previously, this distribution did not fit the analyzed experimental data in a proper manner, but if it is used to estimate a technological LB value, six specimens seems to be enough for such purpose (Table 8).
The methods that require data censoring or data corrections for stable crack growth or large scale plasticity, presented unacceptable LB values. This does not mean that they are incorrect, but the aim in this paper was to perform an analysis on each method for raw data without any kind of corrections. Another future step in our project will be to consider the above mentioned corrections, in order to figure out if it is more simple and convenient a methodology that analyzes many experimental data without corrections, or one that requires a lower number of experimental data but using a more complicate testing technique or even more complex statistical analysis.
V. CONCLUSIONS
1. A great scatter in the calculated LB values was generally obtained when a small number of specimens was considered. This scatter diminished when "n" was increased.
2. The number of specimens necessary to have acceptable LB was indeed a lot higher than the usual number of tests that are performed for material characterization (at least six specimens for most of the analyzed methods). This number depends both on the method used for such determination and on the data set itself.
3. The SPRÖDZON method seems to be the best one for a technological LB estimation.
4. Landes et al. proposal does not seem to be good enough, because, depending of the toughness value used for the LB calculation, it can vary from very conservative to non conservative.
5. The method that presented the worst results was the one that estimated the LB as a 3% failure probability using the fixed-parameter Weibull distribution.
Aknowledgements: To Conicet.
REFERENCES
1. Anderson, T.L., D. Stienstra, and R.H. Dodds, "A Theoretical Framework for Addressing Fracture in the Ductile-Brittle Transition Region," Fracture Mechanics - 24 th Volume, STP 1207, 186-214 (1994). [ Links ]
2. ASTM E 1921. Standard Test Method for determination of Reference Temperature, T0, for Ferritic Steels in the Transition Range. ASTM , Annual Book of Standards, Vol. 03.01 (1997). [ Links ]
3. Hauge, M., C. Thaulowl, F. Minami and M. Toyoda, "Estimation Lower Bound CTOD Fracture Toughness of HAZ Notched Welds with Mechanical Mismatch," Tenth European Conference on Fracture ECF 10, 1027-1039 (1994). [ Links ]
4. Heerens, J., U. Zerbst, and K.H. Schwalbe, "Strategy for Characterizing Fracture Toughness in the Ductile to Brittle Transition Regime," Fatigue Fract. Engng. Mater. Struct., 16 (11): 1213-1230 (1993). [ Links ]
5. Heerens J., Pfuff M., Hellmann D., Zerbst U., "The Lower Bound Toughness Procedure Applied to the Euro Fracture Toughness Dataset," Engineering Fracture Mechanics, Vol 69, 483-495 (2001). [ Links ]
6. Iwadate, T., Y. Tanaka, S. Ono, and J. Watanabe, "An Analysis of Elastic-Plastic Fracture Toughness Behavior for JIC Measurement in the Transition Region," Elastic-Plastic Fracture: Second Symposium, Vol. II- Fracture Resistance Curves and Engineering Applications, ASTM STP 803, 531-561 (1983). [ Links ]
7. Iwadate, T. and T. Yokobori, "Evaluation of Elastic-Plastic Fracture Toughness Testing in the Transition Region Though Japanese Interlaboratory Tests," Fracture Mechanics - 24 th Volume, ASTM STP 1207, 233-263 (1994). [ Links ]
8. Landes, J.D. and D.H. Shaffer, "Statistical Characterization of Fracture in the Transition Region," Fract.Mech., 12th Conference, ASTM STP 700, 368-382 (1980). [ Links ]
9. Landes, J.D. and D.E. McCabe, "The Effect of Section Size on the Transition Temperature of Structural Steels," Scientific Paper 82-ID-Metal-P2, Westinghouse RD Center, (1982). [ Links ]
10. Landes, J.D. "A Two Criteria Statistical Model for Transition Fracture Toughness," Fatigue Fract. Engng. Mater. Struct., 16 (11): 1161-1174, (1993). [ Links ]
11. Landes, J.D., U. Zerbst, J. Heerens, B. Petrovski, and K.H. Schwalbe, "Single-Specimen Test Analysis to Determine Lower-Bound Toughness in the Transition," Fracture Mechanics - 24th. Volume, ASTM STP 1207, 171-185 (1994). [ Links ]
12. Moskovic R, "Modelling of Fracture Toughness Data in the Ductile to Brittle Transition Temperature Region by Statistical Analysis," Engng Fracture Mech,Vol6, 511-530 (2002). [ Links ]
13. Perez Ipiña, J.E., S.M.C. Centurion, and E. Asta, "Minimum Number of Specimens to Characterize Fracture Toughness in the Ductile-to-Brittle Transition Region," Engng. Fracture Mechanics, 47 (3): 457-463 (1994). [ Links ]
14. Van Der Sluys W.A. and M.T. Miglin, "Results of MPC/JSPS Cooperative Testing Program in the Brittle-to-Ductile Transition Region," Fracture Mechanics - 24 th Volume, ASTM STP 1207, 308-324 (1994). [ Links ]
15. Wallin, K., "Statistical Modelling of Fracture in the Ductile to Brittle Transition Region," European Symposium on Elastic-Plastic Fracture Mechanics: Elements of Defect Assessment, 1-27 (1989a). [ Links ]
16. Wallin, K., "A Simple Theoretical Charpy V-KIC Correlation for Irradiation Embrittlement," ASME Pressure Vessels and Piping Conference, Innovative Approaches to Irradiation Damage and Fracture Analysis, PVP-Vol. 170, ASME, (1989b). [ Links ]
17. Wallin, K. and M. Hauge, "Improved Methodology to Determine Lower Bound HAZ CTOD Toughness," 9th European Conference on Fracture, ECF 9 (1992). [ Links ]
18. Wallin, K., "Statistical Aspects of Constraint with Emphasis on Testing and Analysis of Laboratory Specimens in the Transition Region," Constraint Effects in Fracture, ASTM STP 1171, 264-288 (1993). [ Links ]














