Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.35 n.1 Bahía Blanca ene./mar. 2005
On the viscosity of concentrated suspensions of charged colloids
C. L. A. Berli,1, 2 J. A. Deiber1 and D. Quemada3
1 INTEC (Universidad Nacional del Litoral - CONICET), Güemes 3450, 3000, Santa Fe, Argentina
2 Departamento de Física, Facultad de Bioquímica y Ciencias Biológicas, UNL, El Pozo, 3000, Santa Fe, Argentina
3 LBHP, Université Paris VII (CNRS ESA 7057), Case 7056, 2 Place Jussieu, 75251 Paris Cedex 05, France
Abstract ¾ This work is concerned with the theoretical estimation of the low-shear viscosity of concentrated suspensions of charged-stabilized latex particles. Calculations are based on the assumption that particles interacting through purely repulsive potentials behave as equivalent hard-spheres (HS), and suspension viscosity may be analyzed in the framework of HS systems. In order to predict numerically the HS radius, the pair potential due to double-layer interaction, as a function of particle concentration, was investigated by using Poisson-Boltzmann theory and the cell model. Calculations explain appropriately experimental data for a wide range of particle sizes, volume fractions and salt concentrations. The problem concerning the effective surface charge of latex particles is also discussed.
Keywords ¾ Suspension Viscosity. Hard-Sphere Radius. Charged Colloids. Double-Layer Interaction.
I. INTRODUCTION
The connection between rheological functions and the microstructure of colloids is a subject of interest for both the basic scientific problem and the industrial applications. At present, it is well understood that the structure of colloidal dispersions, and hence the flow behavior, is determined by the nature of the interaction forces (Russel et al., 1991; Hunter, 1992; Tadros, 1996; Quemada and Berli, 2002). Nevertheless, appropriate modeling is still required to attain quantitative predictions of viscosity in terms of physicochemical characteristics of the medium. For this purpose, the study of particle-particle interactions is a crucial aspect. Since rigorous calculations of rheological functions can be made mainly in situations where the colloidal structure is not affected significantly, the analysis here concern viscosity in the limit of very low shear stress.
The structure of colloidal suspensions of rigid spheres strongly resembles that of atomic fluids (Hunter, 1992; Tadros, 1996; Arora and Tata, 1998). More precisely, dilute suspensions are like a gas, where particles move freely throughout the medium, and concentrated suspensions are like a liquid, where the movement of particles is constrained by the neighbors. It is clear that, in colloidal suspensions, the space among particles is filled by the suspending fluid, particles are driven by Brownian motion and diffusivity is controlled by hydrodynamic interactions. In this context, significant progress has been made in the comprehension of colloidal suspensions composed of spherical particles, without surface forces, dispersed in a Newtonian fluid of viscosity hF (see, for instance, Heyes and Sigurgeirsson, 2004). At high particle concentration, the low-shear viscosity of the suspension (h0) is related to the particle volume fraction (f) through the following equation,
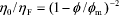 , (1)
, (1)
where fm is the volume fraction at which the viscosity diverges and a fluid-to-solid transition occurs (Krieger, 1972; Quemada, 1977; Brady, 1993). For monodisperse and rigid spheres, fm corresponds to the glass transition volume fraction, fG » 0.58 (see Quemada and Berli, 2002, and references therein).
An additional contribution to the viscosity arises when the suspended particles are electrostatically charged and the electrical double-layers (EDL) developed. In dilute suspensions, this contribution comes into play through the so-called primary and secondary electroviscous effects (Russel, 1978; Rubio-Hernández et al., 2004). In concentrated suspensions, the overlapping of EDL yields strong repulsive forces that control phase behavior and rheology. In particular, the interaction substantially increases suspension viscosity and shifts the fluid-to-solid transition to values of f lower than fG. To interpret experimental results, a common idea in colloid science is that EDL interaction increases the effective radius of particles, and hence the effective volume fraction (Russel et al., 1991; Hunter, 1992; Tadros, 1996; Bergenholtz et al., 1998; Horn et al., 2000; Fritz et al., 2002; Philipse and Koenderink, 2003). The theoretical basis of this idea can be found in the approaches used for the treatment of atomic systems (McQuarrie, 1976). In fact, the structure of dense fluids is determined basically by the repulsive part of the pair potential (Chandler et al., 1983). In addition, interaction potentials U(R) that decay rapidly with distance R can be represented as a cut-off potential at the distance of closest approach, Rc = 2aHS. Thus aHS defines the so-called hard-sphere (HS) radius of molecules. In the perturbation theory of Barker and Henderson (1967), aHS is given by the following relation,
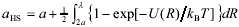 | , (2) |
where a is the actual particle radius, kB is the Boltzmann constant, T is the absolute temperature and l is the distance at which the interaction vanishes. This definition of aHS ensures that the Helmholtz free energy of a liquid is equal to that of a HS system to the first term in an expansion of the free energy. The successful applications of this approach are well described in the revision of Chandler et al. (1983). Recently, the same formula for aHS was derived from entirely different criteria (Rickayzen et al., 2003).
Therefore, by analogy to the treatment of atomic liquids, colloidal particles interacting through purely repulsive potentials are considered to have an equivalent HS radius, which includes the thickness of an exclusion layer due to repulsive forces. One may further assume that there exists an equivalent HS system that accounts for the suspension viscosity as  , where
, where  is the HS volume fraction. This allows one to use the knowledge gained on HS systems to deal with more complex suspensions. Basically, a system involving both hydrodynamic and thermodynamic interactions is reduced to an equivalent system involving only hydrodynamics. Nevertheless, the crucial aspect here is the correct determination of HS from U(R). In this sense, when applying the HS concept to colloids, it is clear that Eq. (2) must be used with steeply decaying potentials, as in the case of polimerically stabilized particles (Mewis et al., 1989). For EDL interaction, the approach is rigorously valid when the range of the interaction is short in relation to particle size, a situation reached at high ionic strength (Buscall, 1991; Quemada, 1994). At low ionic strength, the curve U(R) decays slowly and the exclusion distance is more difficult to determine precisely (particles interacting through such soft potentials are called soft spheres). On the other hand, in relation to the viscosity equation, the approach is reliable for aHS slightly higher than a. According to Brady (1993), longer ranged interactions (soft spheres) could lead to a different scaling in the relationship h0(f ).
is the HS volume fraction. This allows one to use the knowledge gained on HS systems to deal with more complex suspensions. Basically, a system involving both hydrodynamic and thermodynamic interactions is reduced to an equivalent system involving only hydrodynamics. Nevertheless, the crucial aspect here is the correct determination of HS from U(R). In this sense, when applying the HS concept to colloids, it is clear that Eq. (2) must be used with steeply decaying potentials, as in the case of polimerically stabilized particles (Mewis et al., 1989). For EDL interaction, the approach is rigorously valid when the range of the interaction is short in relation to particle size, a situation reached at high ionic strength (Buscall, 1991; Quemada, 1994). At low ionic strength, the curve U(R) decays slowly and the exclusion distance is more difficult to determine precisely (particles interacting through such soft potentials are called soft spheres). On the other hand, in relation to the viscosity equation, the approach is reliable for aHS slightly higher than a. According to Brady (1993), longer ranged interactions (soft spheres) could lead to a different scaling in the relationship h0(f ).
It should be mentioned here that a different model has been proposed in the literature to relate EDL interaction to suspension viscosity (Goodwin et al., 1982; Ogawa et al., 1997). In this approach, h0 is calculated by adding the contributions from hydrodynamic and thermodynamic interactions, the last one being estimated from the theory of the activation processes. A difficulty found in this model is the presence of several unknown proportionality constants.
The aim of the present work is to estimate theoretically the low-shear viscosity of aqueous suspensions of electrostatically charged latex particles. For this purpose, we suggest that the HS concept applies for the overall range of particle concentrations and ionic strengths, if an appropriate expression of U(R) is considered. It is worth noting here that the classical calculation of EDL interaction (DLVO theory) is not sensitive to f. Therefore, we investigated the interaction between charged particles in a concentrated state. Calculations were made by using linear Poisson-Boltzmann (PB) theory in the framework of the cell model (CM). The pair potential thus obtained describes appropriately the low-shear viscosity with the most significant parameters of latex suspensions, namely, particle volume fraction and salt concentration. Since a major problem in the study of charged colloids is the determination of the surface charge that enters modeling equations, emphasis is placed here in the analysis of the effective surface charge displayed by latex particles.
II. EXPERIMENTAL DATA
A. Sample characteristics
Experimental data from aqueous suspensions of monodisperse poly-styrene (PS) particles are considered. The synthesis and characterization of these particles were made by Richtering and co-workers and are well described elsewhere (Horn et al., 2000). PS particles were obtained by soap-free emulsion polymerization, using pure water as the reaction medium. Particle size was determined from quasyelastic light scattering measurements and titration of the acidic surface groups was carried out with a conductometric titrator using KOH solutions. Data relevant for the purposes of this work are presented in Table 1. In addition, here we revise the suspensions preparation method in order to quantify properly the concentration of ions in solution. Concentrated suspensions of volume fraction fc were subjected to dialysis against KCl solutions of defined ionic strength. Thus the average concentration of ions can be calculated according to the Donnan equilibrium established through the membrane (Bergenholtz et al., 1998),
 | , (3) |
where np = 3f /4pa3 is the number of particles per unit volume and ns = 103NA[KCl] is the salt density used as dialyzate, NA being the Avogadro's number. After dialysis, concentration series were prepared by diluting the concentrated suspension with the solution used as dialyzate. Therefore, the final concentration of ions in suspensions of volume fraction f is given by,
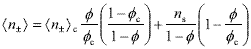 | . (4) |
B. The problem of effective charges
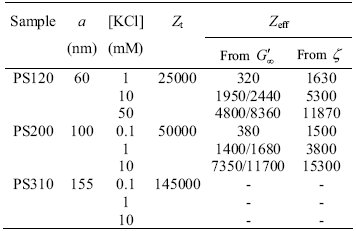
The electrostatic charge of the particles here considered is due to dissociation of sulfate groups attached to particle surfaces, the number of which is evaluated by titration (Zt in Table 1). This number is assumed to represent the actual surface charge number Z, also designated bare or structural charge, provided the acidic groups are fully dissociated. Nevertheless, the dynamics of charged colloids, as observed in rheometry, electrophoresis, conductivity and light scattering experiments, appears to be governed by an effective charge Zeff that is smaller in magnitude than Z (Belloni, 1998; Hansen and Löwen, 2000; Levin, 2002; Quesada-Pérez et al., 2002). This is clearly observed in data reported in Table 1. The magnitude of Zeff also depends on the method of determination due to the role that the surrounding double-layer of ions plays under different experimental conditions (Attard et al., 2000; Wette et al., 2002; Tirao-Miranda et al., 2003). An additional feature is that Zeff increases with salt concentration, an effect also called atypical electrophoretic mobility behavior (Bergenholtz et al., 1998).
The concept of ion condensation is widely used to interpret this phenomenon (Belloni, 1998; Hansen and Löwen, 2000; Schmitz, 2000; Levin, 2002; Quesada-Pérez et al., 2002). In highly charged systems, the electrolyte ions are subjected to an electrostatic interaction higher than the thermal energy. Hence counterions are strongly attracted to the surfaces and accumulate in a thin layer around the particle. The result is an apparent surface charge that is lower than the bare charge. This mechanism also explains the variation of Zeff with added salt: at high ionic strength the surface charge is well screened by the ionic cloud and counterions condensation is relatively less important.
Although the important efforts made (see, for instance, the procedure known as charge renormalization proposed by Alexander et al., 1984), an 25 accurate estimation of the effective surface charge of colloids is still lacking.
Table 1. Main characteristics of the latex suspensions studied (Horn et al., 2000). Zt is the number of surface charges per particle from conductimetric titration and Zeff is the effective number from data of both high frequency dynamic modulus (G'¥) and z-potential.
C. Viscosity data and the effective particle radius
Viscosity measurements were carried out with a RSFII rheometer (Rheometrics) using a Couette cell, in steady-shear conditions, at 20oC (Horn et al., 2000). Figure 1 shows suspension viscosity as a function of particle volume fraction, for different salt concentrations. It is observed that, for a given f, h0 increase substantially as the ionic strength decreases. Accordingly, h0 diverges at lower volume fractions as the ionic strength decreases. These results are well known for charged colloids. Furthermore, at very low ionic strength, repulsive forces are long ranged enough to produce order at low I, that is, particles arrange in crystal-like structures that entail elasticity and yield stress (Russel et al., 1991; Arora and Tata, 1998).
To interpret these results, it is considered that particles have an effective radius that includes the exclusion distance due to repulsive forces, as discussed in Section I. Here we define aeff to be the effective radius exhibited by particles in experiments, to differentiate it from aHS, which is obtained through theoretical calculations. Therefore, assuming that feff = f (aeff /a)3 is the effective volume fraction of particles, aeff can be obtained from viscosity data by using 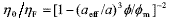 , with fm = 0.58.
, with fm = 0.58.
After inverting this equation, experimental values of h0(f) are readily converted into values of aeff(f)). Symbols in Fig. 2 represent the results for the samples studied. As expected, the ratio aeff/a decreases to 1 with the addition of salt. The main feature to be noted in Fig. 2 is the increase of aeff/a with f. Indeed, accounting for this effect is the main challenge in this work.
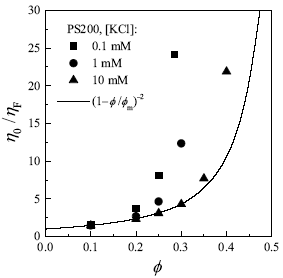
Figure 1. Relative viscosity as a function of volume fraction for aqueous suspensions of latex particles at 20oC. Symbols are data from Horn et al. (2000). The line is the prediction of Eq. (1) with fm = 0.58.
III. THEORETICAL CONCEPTS
A. Calculations involving DLVO interaction
The interaction between charged colloids is normally treated in the theoretical framework of Poisson-Boltzmann model (Russel et al., 1991; Hunter, 1992). For the case of spherical particles carrying a surface charge Ze, where e is the elementary charge, the pair interaction energy is (Verwey and Overbeek, 1948)
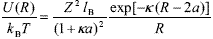 | , (5) |
where k is the inverse Debye length and lB = e2/4pekBT is the Bjerrum length, e being the permittivity of the medium. This equation constitutes the classical Debye-Hückel approximation, on the base 1.10 of which the DLVO theory provides a satisfactory description of different phenomena like colloidal stability and phase transition (Russel et al., 1991; Hunter, 1992). Nevertheless, Eq. (5) is only applicable to systems with very low particle concentration. In fact, its derivation involves a pair of particles in osmotic equilibrium with a large electrolyte reservoir. At high f, the calculation fails because each particle is surrounded by several neighbors and the number of counterions takes importance in relation to the added salt.
Another crucial aspect of Eq. (5) is that it becomes inaccurate in systems containing highly charged particles, where the electrostatic energy of electrolyte ions is higher than the thermal energy. The strategy normally followed is to replace the actual number Z by an effective charge Zeff and restrict the domain of applicability to interparticle separations larger than the range of the interaction, i.e., R - 2a >> k-1 (Belloni, 1998; Hansen and Löwen, 2000; Levin, 2002; Quesada-Pérez et al., 2002). Indeed, as discussed in Section II.B, the determination of Zeff from the characteristics of the suspension is still an open problem in colloid science. Thus a common practice in the literature is to consider Zeff as an adjustable parameter to fit experimental data obtained from different techniques (see, for example, Arora and Tata, 1998; Bergenholtz et al., 1998; Horn et al., 2000; Quesada-Pérez et al., 2002; Wette et al., 2002; Tirao-Miranda et al., 2003).
Following this procedure, one may calculate aHS through Eqs. (2) and (5), adjusting Zeff to match aHS to the values of aeff derived from viscosity. In Eq. (5), we included 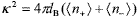 , where the average ion densities come from Eqs. (3) and (4), for a given salt density ns, volume fraction f and charge number Zeff. It was observed that Zeff increases several times as I increases from 0.1 to 0.3. Considering the preparation of these suspensions, there are no physical reasons to expect such a strongly variation of Zeff with f. It should be noted that the ionic strength is nearly constant for a concentration series (Section II.A) and there is no association-dissociation equilibrium (Horn et al., 2000). This result is due to the failure of Eq. (5) to describe experimental data at high f. Under these circumstances, Zeff is merely a fitting parameter that compensates the shortcomings of the approximate calculation.
, where the average ion densities come from Eqs. (3) and (4), for a given salt density ns, volume fraction f and charge number Zeff. It was observed that Zeff increases several times as I increases from 0.1 to 0.3. Considering the preparation of these suspensions, there are no physical reasons to expect such a strongly variation of Zeff with f. It should be noted that the ionic strength is nearly constant for a concentration series (Section II.A) and there is no association-dissociation equilibrium (Horn et al., 2000). This result is due to the failure of Eq. (5) to describe experimental data at high f. Under these circumstances, Zeff is merely a fitting parameter that compensates the shortcomings of the approximate calculation.
B. Calculation proposed forconcentrated systems
In this context of results, the idea in the present work is to derive a f-dependent pair potential to be used in Eq. (2). For this purpose, one may take advantage of the fact that highly repulsive particles form ordered structures, hence the CM applies (Alexander et al., 1984; van der Vorst et al., 1995; Levin, 2002). In this approach, each
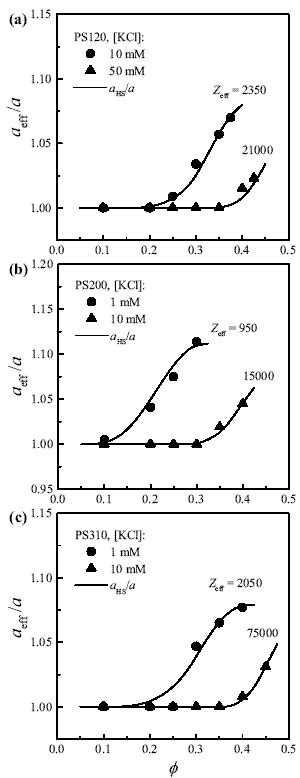
Figure 2. Effective particle radius as a function of volume fraction, for different salt concentrations. The actual particle radii are: (a) 60 nm; (b) 100 nm; (c) 155 nm. Symbols are values calculated from viscosity data. The lines are the predictions of Eqs. (2) and (9).
particle and its related ions are considered to be confined to a spherical Wigner-Seitz cell of radius b ~ af-1/3, as shown in Fig. 3a. Due to the periodicity of the system, the calculations carried out in the domain of one cell are assumed to be valid for the whole colloid. In principle, the Wigner-Seitz cell is a polyhedron that represents the space occupied by a single atom in a crystal, involving the full symmetry of the lattice. Here we use this framework to calculate the pair interaction of charged particles in a concentrated environment, thus avoiding the many body problem.
The calculation of the EDL interaction involves both osmotic pressures and electric stresses (Verwey and Overbeek, 1948; Russel et al., 1991; Hunter, 1992). In the case of two spherical particles, as a consequence of curvature, the algebraic problem cannot be solved readily. Thus a procedure frequently used in the literature is the Derjaguin approximation (Hunter, 1992), which requires the calculation of the force between flat surfaces. Accordingly, here we consider a system of flat cells, i.e., a series of charged plates organized in a parallel arrangement perpendicular to the x-direction, as shown in Fig. 3b (see also Hansen and Löwen, 2000). The size of the plates is very large in comparison to the cell width b'. The electrostatic potential y in the cell is governed by PB equation,
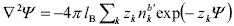 | , (6) |
where Y = ey /kBT is the normalized potential and the sub-index k indicates positive (+) or negative (-) ions. Also in this equation, zk are the ion valences and  are the ion densities at the cell surface, where the potential is defined to be Y(b') = 0.
are the ion densities at the cell surface, where the potential is defined to be Y(b') = 0.
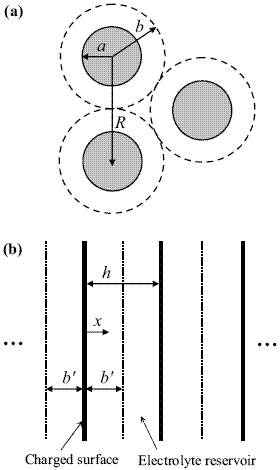
Figure 3. Schematic representations of (a) spherical Wigner-Seitz cells and (b) one-dimensional cells.
Because of symmetry, when the surface-to-surface separation h is equal to 2b' (Fig. 3b) there is no net force on the plates. Instead, when two surfaces approach one another (h < 2b') a repulsive force arises due to the osmotic pressure p generated by the accumulation of ions in the inner region between the plates. At equilibrium, the osmotic and electric forces balance according to the following expression (Verwey and Overbeek, 1948; Russel et al., 1991; Hunter, 1992),
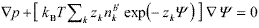 | , (7) |
In the case of flat plates, the electric stress is zero at the midplane between the approaching surfaces. Thus Eq. (7) can be integrated to obtain the pressure difference between the midplane ( x = h/2 ) and the plane of reference ( x = b' ), that is,
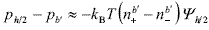 | , (8) |
where Yh/2 << 1 is the midplane potential. For small degrees of double-layer overlap, Yh/2 can be approximated by adding the single potentials Y(x) due to each plate (Hunter, 1992), i.e., Yh/2 » 2Y(x = h/2). The calculation of Y(x) for the flat cells is carried out in Appendix A. In particular, instead of the classical Debye-Hückel approximation, here PB equation was linearized about the average potential  in the cell (Deserno and von Grünberg, 2002). The advantage of this linearization is that Y(x) is written in terms of
in the cell (Deserno and von Grünberg, 2002). The advantage of this linearization is that Y(x) is written in terms of 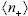 and
and  , hence the calculation of ion densities at the cell border is avoided.
, hence the calculation of ion densities at the cell border is avoided.
The derivation of the interaction energy between curved surfaces, starting from the knowledge of the force per unit area between flat surfaces ( ph/2 - pb' ), is presented in Appendix B. The procedure described in classical books was followed (Verwey and Overbeek, 1948; Hunter, 1992), with the additional constraints posed by the CM. The pair interaction thus obtained is,
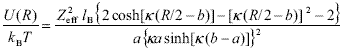 | , (9) |
where 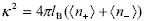 and b is the cell radius corresponding to the spherical geometry (Fig. 3a). On the base that well-stabilized suspensions form crystal-like structures, here the cell radius is considered to be b = a(0.74 / f)1/3 , where 0.74 is the maximum packing fraction usually found in concentrated latices at low ionic strength (Alexander et al., 1984; van der Vorst et al., 1995; Arora and Tata, 1998). Taking into account the concepts discussed in Section II.B, the set formed by the particle plus condensed counterions is here considered as a single entity carrying an effective surface charge. Further, Zeff is the only parameter not known a priori in the model.
and b is the cell radius corresponding to the spherical geometry (Fig. 3a). On the base that well-stabilized suspensions form crystal-like structures, here the cell radius is considered to be b = a(0.74 / f)1/3 , where 0.74 is the maximum packing fraction usually found in concentrated latices at low ionic strength (Alexander et al., 1984; van der Vorst et al., 1995; Arora and Tata, 1998). Taking into account the concepts discussed in Section II.B, the set formed by the particle plus condensed counterions is here considered as a single entity carrying an effective surface charge. Further, Zeff is the only parameter not known a priori in the model.
Therefore, Eq. (9) accounts for the interaction energy between charged particles in a concentrated environment, as derived in the context of the CM and linear PB theory. The most relevant feature of this interaction potential, in relation to classical calculations, is that it strongly depends on particle concentration through the parameter b. In addition, the model captures the fact that particles placed at the center of spherical cells are in the minimum of potential energy generated by the neighbors (the interaction vanishes at R = 2b). Because of the approximations made in the calculations above, Eq. (9) is limited to situations in which the Debye length is smaller in magnitude than the free space in the cell, more precisely, k-1 << (b - a) . For example, for systems with f = 0.1, ka must be higher than 5, approximately. It is appropriate to remark here that also Eq. (2) becomes inaccurate at very low ionic strength, due to the smoothness of the potential curve.
IV. RESULTS AND DISCUSSION
The numerical predictions of aHS for the latex suspensions studied are included in Fig. 2 (solid lines). Calculations were carried out through the following procedure. First, the values of 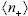 and
and  for a given suspension were obtained through Eqs. (3) and (4), where the input data are a, f, ns and Zeff, the last one being the only unknown. The interaction U(R) was obtained from Eq. (9) and then Eq. (2) was integrated numerically to obtain aHS. The value of Zeff was adjusted to provide the best fit to experimental data. One may observe that the curves of aHS/a as a function of f present a remarkable agreement with data for different particle sizes and salt contents. It should be stressed that, for a given ionic strength, the same value of Zeff (reported in Fig. 2) was found for the whole range of f, as expected for a consistent modeling of this type of suspensions (Quesada-Pérez et al., 2002). Further, the values of Zeff compare reasonably well to those obtained previously from different techniques (Table 1). Data from suspensions with very low salt content (for example, PS200, 0.1 mM; Fig. 1) were not included in Fig. 2 because they do not satisfy the condition k-1 << (b - a) required to apply Eq. (9).
for a given suspension were obtained through Eqs. (3) and (4), where the input data are a, f, ns and Zeff, the last one being the only unknown. The interaction U(R) was obtained from Eq. (9) and then Eq. (2) was integrated numerically to obtain aHS. The value of Zeff was adjusted to provide the best fit to experimental data. One may observe that the curves of aHS/a as a function of f present a remarkable agreement with data for different particle sizes and salt contents. It should be stressed that, for a given ionic strength, the same value of Zeff (reported in Fig. 2) was found for the whole range of f, as expected for a consistent modeling of this type of suspensions (Quesada-Pérez et al., 2002). Further, the values of Zeff compare reasonably well to those obtained previously from different techniques (Table 1). Data from suspensions with very low salt content (for example, PS200, 0.1 mM; Fig. 1) were not included in Fig. 2 because they do not satisfy the condition k-1 << (b - a) required to apply Eq. (9).
It should be also mentioned that aHS reaches a maximum and then decreases with f (not shown in Fig. 2). This is a consequence of the variation of U(R) with f given by Eq. (9). Indeed, since U(2b) = 0, the cell radius b sets a boundary marks for aHS. Thus the possible situation in which f(aHS/a) 3 > 0.74 is avoided, in contrast to the unphysical results obtained when Eq. (2) is integrated with the classical DLVO potential.
The results of modeling the suspension viscosity are summarized in Fig. 4, where it is observed that all viscosity data (different particle size and salt content) condensate onto a master curve when the volume fraction is rescaled with the factor (aHS/a)3, i.e., when h0 is plotted as a function of fHS. Therefore, it may be said that there exists an equivalent HS system, the viscosity of which successfully represents that of the suspensions of charge-stabilized latex particles.

Figure 4. Viscosity master curve for aqueous suspensions of latex particles at 20oC. The equivalent HS radius is calculated through Eqs. (2) and (9) with the values of Zeff reported in Fig. 2.
V. CONCLUSIONS AND FURTHER RESEARCH
In this work, an expression of the pair potential due to the EDL interaction in concentrated colloids is investigated, in order to interpret theoretically the effective radius exhibited by charged latex particles suspended in water, as obtained from low-shear viscosity data. Calculations were performed by using linear PB theory, with the additional feature that particles were considered to be placed into spherical cells, in contrast to the infinitely large reservoir considered in classical DLVO calculations. This introduces the effect of particle concentration on EDL interaction. With this novel potential, the equation of Barker and Henderson predicts appropriately the equivalent HS radius for latex particles as a function of volume fraction, for different particle sizes and salt concentrations. The effective number of surface charges per particle, which is in principle unknown in our modeling, was adjusted to provide the best fit to experimental data. To close the model, one should face the problem of predicting Zeff from Zt. Indeed, understanding the interplay between the surface charge obtained by titration and that governing the physics of the system is a challenging task that still deserves further efforts in colloid science.
In a more general context, we are proposing here a theoretical connection between the low-shear viscosity and the physicochemical parameters of the suspension through: (i) the viscosity-volume fraction relation given by Eq. (1), (ii) the concept of equivalent HS radius for repulsive colloids, quantified with Eq. (2), and (iii) an expression of the EDL interaction in concentrated systems, such as that given by Eq. (9). The derivation of this last equation involves approximations and hence several improvements could be made. Nevertheless, one may observe that the modeling proposed captures the main features underlying the physics of charged colloids in concentrated suspensions and thus gives a satisfactory description of the low-shear viscosity for a wide range of particle concentrations.
APPENDIX
A. Electrostatic potential in one-dimensional cells
It is known that the linearization of PB equation normally used in colloid science (Debye-Hückel approximation) works well at large distances from the charged surface only. Nevertheless, this approximation is not the only one possible to simplify the treatment of EDL interaction: the right hand side of Eq. (6) could be linearized about any potential 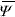 in the cell domain. In particular, here we linearize PB equation about the average potential
in the cell domain. In particular, here we linearize PB equation about the average potential  , as recently proposed in the literature (Deserno and von Grünberg, 2002). One benefit of this procedure is that the potential can be written in terms of the average ion densities.
, as recently proposed in the literature (Deserno and von Grünberg, 2002). One benefit of this procedure is that the potential can be written in terms of the average ion densities.
Following we consider the system of flat cells shown in Fig. 3b ( 0 £ x £ b', x being the Cartesian coordinate) with the boundary conditions: Y(b') = 0 and ¶Y/¶x = 0 for x = b'. The ion density profiles in the cell are determined by Boltzmann distribution,
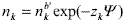 | (A1) |
For a given potential 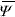 , the corresponding density values are
, the corresponding density values are 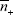 and
and 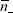 . Linearizing Eq. (A1) about
. Linearizing Eq. (A1) about 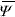 leads to,
leads to,
 . (A2)
. (A2)
Then including Eq. (A2) into Eq. (6) and considering a symmetric electrolyte ( z+ = -z_ = z ) yields,
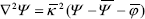 , (A3)
, (A3)
with  and
and  . Solving Eq. (A3) gives the potential for a charged plane,
. Solving Eq. (A3) gives the potential for a charged plane,  . By averaging both sides of Eq. (A2) in the cell domain one obtains,
. By averaging both sides of Eq. (A2) in the cell domain one obtains,
 . (A4)
. (A4)
Further, selecting 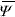 =
=  , Eq. (A4) yields
, Eq. (A4) yields  (Deserno and von Grünberg, 2002). Consequently, the firstly unspecified values
(Deserno and von Grünberg, 2002). Consequently, the firstly unspecified values 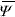 ,
, 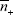 and
and 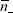 can be taken as the respective average values in the cell. Thus the potential of each plate is simply,
can be taken as the respective average values in the cell. Thus the potential of each plate is simply,
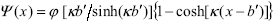 , (A5)
, (A5)
with j and k written n terms of 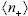 and
and  , which are known from the suspension preparation method (Section II.A). In addition, j is related to the surface charge density q, by including the charge balance condition in the cell volume,
, which are known from the suspension preparation method (Section II.A). In addition, j is related to the surface charge density q, by including the charge balance condition in the cell volume,  .
.
B. Interaction energy in spherical cells
The midplane potential required in Eq. (8) can be introduced as Yh/2 ≈ 2Y(x = h/2) (Hunter, 1992), with Y(z) given by Eq. (A5). Consistently, the densities  in Eq. (8) are introduced in terms of
in Eq. (8) are introduced in terms of 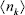 . Thus,
. Thus,
 . (A6)
. (A6)
This pressure difference is directly the force per unit area that pushes the charged surfaces apart when h < 2b'. The interaction energy associated to this force is,
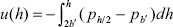 | . (A7) |
Solving Eq. (A7) after introducing Eq. (A6) yields the interaction energy per unit area between the charged plates in the array of Fig. 3b. The last step is the calculation of the interaction energy between spherical particles by using Derjaguin approximation (Hunter, 1992), that is,
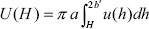 | . (A7) |
where H = R - 2a is the surface-to-surface distance between particles. Introducing the result of Eq. (A7) into Eq. (A8) leads to the expression of the interaction energy reported in Section III.B (Eq. (9)), which includes the geometrical conversion b' ® (b - a).
Further, since quantitative treatment of experiments with linear PB theory requires the use of effective charges, the surface charge density was included as q = - Zeff e/4pa2.
ACKNOWLEDGEMENTS
D.Q. whishes to thank Prof. W. Richtering for kindly providing the rheological data. This research was supported by SEPCYT-FONCyT (PICT 09-09752), SeCyT-UNL (CAI+D 2002) and CONICET (PEI 6526), Argentina.
REFERENCES
1. Alexander, S., P.M. Chaikin, P. Giant, G.J. Morales, P. Pincus, and D. Hone, "Charge renormalization, osmotic pressure and bulk modulus of colloidal crystals: Theory", J. Chem. Phys., 80, 5776-5781 (1984). [ Links ]
2. Arora, A.K. and B.V.R. Tata, "Interactions, structural ordering and phase transitions in colloidal dispersions", Adv. Colloid Interface Sci., 78, 49-97 (1998). [ Links ]
3. Attard, P., D. Antelmi and I. Larson, "Comparison of the zeta potential with the diffuse double layer potential from charge titration", Langmuir, 16, 1542-1552 (2000). [ Links ]
4. Barker, J.A. and D. Henderson, "Perturbation theory and equation of state for fluids. II. A successful theory of liquids", J. Chem. Phys., 47, 4714-4721 (1967). [ Links ]
5. Belloni, L., "Ionic condensation and charge renormalization in colloidal suspensions", Coll. Surf. A: Physicochem. Eng. Aspects, 140, 227-243 (1998). [ Links ]
6. Bergenholtz, J., N. Willenbacher, N.J. Wagner, B. Morrison, D. van den Ende and J. Mellema, "Colloidal charge determination in concentrated liquid dispersions using torsional resonance oscillation", J. Colloid Interface Sci., 202, 430-440 (1998). [ Links ]
7. Brady, J.F., "The rheological behavior of concentrated colloidal dispersions", J. Chem. Phys., 99, 567-581 (1993). [ Links ]
8. Buscall, R.J., "Effect of long-range repulsive forces on the viscosity of concentrated latices: Comparison of experimental data with an effective hard-sphere model", Chem. Soc., Faraday Trans., 87, 1365-1370 (1991). [ Links ]
9. Chandler, D., J.D. Weeks and H. Andersen, "Van der Waals picture of liquids, solids and phase transitions", Science, 220, 787-794 (1983). [ Links ]
10. Deserno, M. and H.-H. von Grünberg, "The osmotic pressure of charged colloidal suspensions: A unified approach to linearized Poison-Boltzmann theory", Phys. Rev. E, 66, 011401-011416 (2002). [ Links ]
11. Fritz, G., V. Schändler, N. Willembacher and N. Wagner, "Electrosteric stabilization of colloidal dispersions", Langmuir, 18, 6381-6390 (2002). [ Links ]
12. Goodwin, J.W., T. Gregory and J.A. Stile, "A study of some of the rheological properties of concentrated polystyrene latices", Adv. Colloid Interface Sci., 17, 185-195 (1982). [ Links ]
13. Hansen, J.-P. and H. Löwen, "Effective interactions between electric double layers", Annu. Rev. Phys. Chem., 51, 209-242 (2000). [ Links ]
14. Heyes D.M. and H. Sigurgeirsson, "The Newtonian viscosity of concentrated stabilized dispersions: Comparisons with the hard sphere model", J. Rheol., 48, 223-248 (2004). [ Links ]
15. Horn, F.M., W. Richtering, N. Bergenholtz, N. Willenbacher and N.J. Wagner, "Hydrodynamic and colloidal interactions in concentrated charge-stabilized polymer dispersions", J. Colloid Interface Sci., 225, 166-178 (2000). [ Links ]
16. Hunter, R., Foundations of Colloid Science, Vols. I and II, Clarendon Press, Oxford (1992). [ Links ]
17. Krieger, I.M., "Rheology of monodisperse latices", Adv. Colloid Interface Sci., 3, 111-136 (1972). [ Links ]
18. Levin, Y., "Electrostatic correlations: from plasma to biology", Rep. Prog. Phys. 65, 1577-1632 (2002). [ Links ]
19. McQuarrie, D.A., Statistical Mechanics, Harper & Row, New York (1976). [ Links ]
20. Mewis, J., W.J. Frith, T.A. Strivens and W.B. Russel, "The rheology of suspensions containing polimerically stabilized particles", AIChE J., 35, 415-422 (1989). [ Links ]
21. Ogawa, A., H. Yamada, S. Matsuda and K. Okajima, "Viscosity equation for concentrated suspensions of charged colloidal particles", J. Rheol., 41, 769-785 (1997). [ Links ]
22. Philipse, A.P. and G.H. Koenderink, "Sedimentation-diffusion profiles and layered sedimentation of charged colloids at low ionic strength", Adv. Colloid Interface Sci., 100-102, 613-639 (2003). [ Links ]
23. Quemada, D., "Rheology of concentrated disperse systems and minimum energy dissipation principle. I. Viscosity concentration relationship", Rheol. Acta, 16, 82-94 (1977). [ Links ]
24. Quemada, D., "Concentrated colloidal suspensions at low ionic strength: a hard-sphere model of zero-shear viscosity, involving the hard-sphere phase transitions", Europhys. Lett., 25, 149-155 (1994). [ Links ]
25. Quemada, D. and C.L.A. Berli, "Energy of interaction in colloids and its implications in rheological modeling", Adv. Colloid Interface Sci., 98, 51-85 (2002). [ Links ]
26. Quesada-Pérez, M., J. Callejas-Fernández and R. Hidalgo-Álvarez, "Interaction potentials, structural ordering and effective charges in dispersions of charged colloidal particles", Adv. Colloid Interface Sci., 95, 295-315 (2002). [ Links ]
27. Rickayzen, G., J.G. Powles and D.M. Heyes, "Viscoelasticity of fluids with steeply repulsive potentials", J. Chem. Phys., 118, 11048-11056 (2003). [ Links ]
28. Rubio-Hernández, F.J., F. Carrique and E. Ruiz-Reina, "The primary electroviscous effect in colloidal suspensions", Adv. Colloid Interface Sci., 107, 51-60 (2004). [ Links ]
29. Russel, W.B., "The rheology of suspensions of charged rigid spheres", J. Fluid Mech., 85, 209-231 (1978). [ Links ]
30. Russel, W.B., D.A. Saville and W.R. Schowalter, Colloidal Dispersions, 2nd edn., Cambridge University Press, Cambridge (1991). [ Links ]
31. Schmitz, K.S., "Effective screened Coulomb charge of spherical colloidal particles", Langmuir, 16, 2115-2123 (2000). [ Links ]
32. Tadros, Th. F., "Correlation of viscoelastic properties of stable and flocculated suspensions with their interparticle interactions", Adv. Colloid Interface Sci., 68, 97-200 (1996). [ Links ]
33. Tirao-Miranda, M., C. Caro-Pérez, M. Quesada-Pérez, J. Callejas-Fernández and R. Hidalgo-Álvarez, "Effective charge of colloidal particles obtained from collective diffusion experiments", J. Colloid Interface Sci., 263, 74-79 (2003). [ Links ]
34. van der Vorst, B., D. van den Ende and J. Mellema, "Linear viscoelastic properties of ordered latices", J. Rheology, 39, 1183-1200 (1995). [ Links ]
35. Verwey, E.J.W. and J.T.G. Overbeek, Theory of the Stability of Liophobic Colloids, Elsevier, Amsterdam (1948). [ Links ]
36. Wette, P., H.J. Schöpe and T. Palberg, "Comparison of colloidal effective charges from different experiments", J. Chem. Phys., 116, 10981-10988 (2002). [ Links ]














