Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.35 n.2 Bahía Blanca abr./jun. 2005
Performance evaluation of maximum likelihood sequence estimation receivers in lightwave systems with optical amplifiers
D. E. Crivelli, H. S. Carrer and M. R. Hueda
Digital Communications Research Laboratory - National University of Córdoba
Av. Vélez Sarsfield 1611 - Córdoba (X5016GCA) - Argentina
{dcrivelli, hscarrer, mhueda}@com.uncor.edu - http://lcd.efn.unc.edu.ar
Abstract ¾ Maximum likelihood sequence estimation (MLSE) has been proposed in earlier literature to combat the effects of nonlinear dispersion in intensity modulation/direct detection (IM/DD) optical channels. In this paper, we develop a theory of the bit error rate (BER) of MLSE-based IM/DD receivers operating in the presence of nonlinear dispersion and amplified spontaneous emission (ASE) noise. We focus on long haul or metro links spanning several hundred kilometers of single mode fibers with optical amplifiers. Numerical results show a close agreement between the predictions of the theory and computer simulations.
Keywords ¾ Maximum Likelihood Sequence Estimation (MLSE). Chromatic Dispersion. Polarization Mode Dispersion. Amplified Spontaneous Emission (ASE) Noise.
I. INTRODUCTION
High-speed fiber optic transmission systems suffer from impairments like chromatic dispersion (CD), polarization mode dispersion (PMD), and amplified spontaneous emission (ASE) noise due to optical amplifiers. The combination of these impairments with the square-law response of the photodetector results in nonlinear intersymbol interference (ISI) and non-Gaussian, signal dependent noise. Due to this nonlinear nature, techniques like feed forward equalization (FFE) or decision feedback equalization (DFE) are severely degraded, whereas maximum likelihood sequence estimation (MLSE) equalization is not (Agazzi et al., 2004a).
MLSE receivers have been widely studied in the context of additive white Gaussian noise (AWGN) channels. Nevertheless, among the properties that require a new study on lightwave systems are the nonlinear nature of the optical channel and the fact that the noise is non-Gaussian and signal-dependent.
MLSE-based receivers have already been reported (Winters and Gitlin, 1990; Haunstein et al., 2001; Agazzi et al., 2004b). Weiss (2003) reported computer simulations of MLSE receivers in the presence of CD, PMD, and ASE noise. A semi-analytical method to evaluate the bit error rate (BER) of MLSE based IM/DD receivers operating in the presence of non-linearities and generic non-Gaussian signal-dependent noise, was introduced by Agazzi et al. (2004b). However, closed-form analytical expressions for the bit error probability similar to those available for AWGN channels (Proakis, 1995) have not been reported so far.
We introduce in this letter a simple analytical expression for the bit error rate in the ASE-limited case, a condition usually satisfied in practice (Agrawal, 1997; Ramaswami and Sivarajan, 2002). Computer simulations show a close agreement with the predictions of our theory. Furthermore, our results are very useful to analyze performance in schemes like turbo equalization and turbo coding.
The rest of the paper is organized as follows. In Section II we present the channel model. A brief description of MLSE receiver is given in Section III. Performance analysis is introduced in Section IV. The predictions of the theory are compared with simulation results in Section V. Conclusions are drawn in Section VI.
II. CHANNEL MODEL
Figure 1 shows a simplified model of the system under consideration. The transmitter modulates the intensity of the signal using a binary alphabet. Let {an} be the sequence of information bits at the input of the optical transmitter ( ). The optical power ratio between the pulses representing a logical 1 and a logical 0 is called the extinction ratio. We assume that the intensity level for a logical 0 (an = 0) is different from zero (i.e., finite extinction ratio), which is usual in practical transmitters (Ramaswami and Sivarajan, 2002). The optical fiber introduces chromatic and polarization mode dispersion, as well as attenuation. Optical amplifiers are deployed periodically along the fiber to compensate for attenuation, but also introduce ASE noise in the signal. The received optical signal is filtered and then converted to a current by a PIN diode or avalanche photodetector. The resulting photocurrent is filtered by an integrate and dump electrical filter (Marcuse, 1990). The output of the filter is sampled at the symbol rate and applied to the MLSE-based detector.
). The optical power ratio between the pulses representing a logical 1 and a logical 0 is called the extinction ratio. We assume that the intensity level for a logical 0 (an = 0) is different from zero (i.e., finite extinction ratio), which is usual in practical transmitters (Ramaswami and Sivarajan, 2002). The optical fiber introduces chromatic and polarization mode dispersion, as well as attenuation. Optical amplifiers are deployed periodically along the fiber to compensate for attenuation, but also introduce ASE noise in the signal. The received optical signal is filtered and then converted to a current by a PIN diode or avalanche photodetector. The resulting photocurrent is filtered by an integrate and dump electrical filter (Marcuse, 1990). The output of the filter is sampled at the symbol rate and applied to the MLSE-based detector.
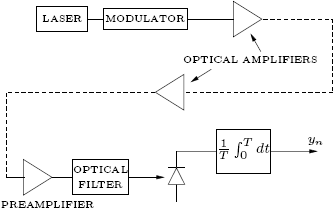
Figure 1: Optical channel model.
The samples of the received electrical signal can be expressed as
yn = In + nn = f(an) + nn, (1)
where In = f(an) represents the noise-free received optical signal, which is in general a nonlinear function of a group of δ consecutive transmitted bits an = (an, an-1, ..., an-δ+1), and nn are samples of the non-Gaussian signal-dependent noise originated by the direct detection process of the optical signal and ASE noise. ASE noise is considered as additive and Gaussian in the optical domain, but due to squaring at the photodiode, it becomes non-Gaussian and signal dependent, and it is characterized by the χ2-distribution (Marcuse, 1990). Thermal noise, shot noise, and noise contributions from any other source are ignored since it is assumed that ASE noise is dominant.
Based on the above considerations, it has been shown that the probability density function (pdf) of yn is given by:
 | (2) |
where Isp is related to the variance of the noise in the optical domain, M is the ratio of the optical to electrical bandwidth of the front-end, and Im(.) is the mth modified Bessel function of the first kind. For a detailed analysis of (2), the reader is referred to (Marcuse, 1990).
III. MLSE DETECTOR
The maximum likelihood sequence detector chooses, among all possible transmitted bit sequences, the sequence {an} that minimizes the metric (Proakis, 1995):
 | (3) |
with ân = (ân, ân-1, ..., ân-δ+1). The analysis and implementation of the receiver can be simplified by using the following approximation for the pdf (2):
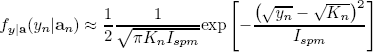 | , (4) |
where  and
and
 | . (5) |
The approximation (4) is derived in (Carrer et al., 2003).
The minimization of (3) can be efficiently implemented using the Viterbi algorithm. Using (4), the expression for the metric required by the Viterbi algorithm can be expressed as
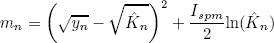 | , (6) |
where  , with În = f(ân).
, with În = f(ân).
IV. PERFORMANCE ANALYSIS
In this section, we analyze the performance of the MLSE described before. Toward this end, we use the expression for the bit error probability of MLSE decoders (Lee and Messerschmitt, 1988) given by1
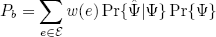 | , (7) |
where  is the set of all error events e starting at a given time instant. Each error event e is characterized by both a correct path Ψ = {an} and an incorrect path
is the set of all error events e starting at a given time instant. Each error event e is characterized by both a correct path Ψ = {an} and an incorrect path  = {ân} that diverges from the correct path at a given time instant and reemerges with the correct path l time instants later. w(e) is the Hamming weight of Ψ Ù
= {ân} that diverges from the correct path at a given time instant and reemerges with the correct path l time instants later. w(e) is the Hamming weight of Ψ Ù  or, in other words, the number of bit errors in the error event (Ù is the exclusive OR operator). Pr{
or, in other words, the number of bit errors in the error event (Ù is the exclusive OR operator). Pr{ |Ψ} is the probability of the error event Ψ ®
|Ψ} is the probability of the error event Ψ ®  (the Viterbi decoder chooses sequence
(the Viterbi decoder chooses sequence  instead of Ψ), and Pr{Ψ} is the probability that the transmitter sent sequence Ψ.
instead of Ψ), and Pr{Ψ} is the probability that the transmitter sent sequence Ψ.
From (6), note that the MLSE-based detector will choose the erroneous path (i.e., Ψ ®  ) if
) if
 | , (8) |
where 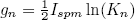 and
and  . After binomial expansion, some manipulation, and replacing
. After binomial expansion, some manipulation, and replacing 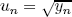 , we obtain
, we obtain
 | , (9) |
where 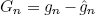 . The probability density function of un can be obtained (Papoulis, 1991) replacing (4) in
. The probability density function of un can be obtained (Papoulis, 1991) replacing (4) in
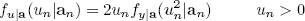 | , (10) |
yielding
 | . (11) |
For high optical signal-to-noise ratio (OSNR) (see (19)), we verify that Pr{|un - 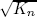 < ξ} ® 1 with ξ > 0 and ξ ® 0. Then, expression (11) can be approximated as
< ξ} ® 1 with ξ > 0 and ξ ® 0. Then, expression (11) can be approximated as
 | . (12) |
From (12) note that un can be considered as a Gaussian variable with mean and variance respectively given by
 | . (13) |
Taking into account the independence of the samples un (given the transmitted sequence), the left side of inequality (9) is a Gaussian variable with mean and variance respectively given by
 | , (14) |
 | . (15) |
To obtain theoretical bounds for the bit error probability, we use the following upper bound for Pr{ |Y} (Lee and Messerschmitt, 1988):
|Y} (Lee and Messerschmitt, 1988):
 | . (16) |
At high OSNR (see (19)), Gn can be neglected, and
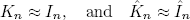 . (17)
. (17)
From the above, and using (14), (15), and (17), it is simple to verify that (16) reduces to
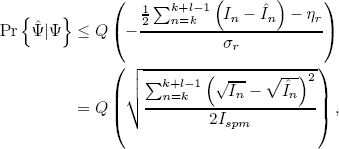 | (18) |
where  . Let I0 and I1 be the current generated by each constellation symbol. Then, defining
. Let I0 and I1 be the current generated by each constellation symbol. Then, defining
- Extinction Ratio :
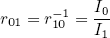
(r01 > 0, see Section II), - Optical Signal-to-Noise Ratio:
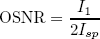 , (19)
, (19) - Normalized OSNR: SNRT
 M OSNR,
M OSNR, 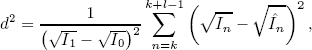
the error event probability (18) can be rewritten as
 | , (20) |
where  . Parameters β and d take into account the reduction of SNRT owing to the extinction ratio and channel dispersion (note that d2 = 1 for optical channels with no dispersion).
. Parameters β and d take into account the reduction of SNRT owing to the extinction ratio and channel dispersion (note that d2 = 1 for optical channels with no dispersion).
Defining dmin as the minimum distance of an error event, and taking into account that w(e) ³ 1, the bit error probability can be lower bounded by (Lee and Messerschmitt, 1988)
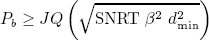 | , (21) |
where  and
and is the set of error events with distance dmin. The lower bound (21) with J = 1 will be used in Section V to evaluate the performance of MLSE-based receivers.
is the set of error events with distance dmin. The lower bound (21) with J = 1 will be used in Section V to evaluate the performance of MLSE-based receivers.
V. SIMULATION RESULTS AND DISCUSSION
In this section, we confirm the theoretical analysis introduced previously by using computer simulations. We present results for a dispersive optical channel with single-mode fiber as specified by the ITU G.652 Recommendation (2003). The latter is used in the third telecommunications window (1550 nm), which leads to a dispersion parameter D = 17 ps/km-nm. We consider a data rate of 10 Gb/s, r10 = 7 and 14 dB, and M = 3. In the following we assume that the transmitted pulse has an unchirped Gaussian envelope exp(-t2/2 ) with unit amplitude and T0 = 36 ps. The MLSE was implemented with an eight-state Viterbi algorithm where a perfect knowledge of the channel response is assumed.
) with unit amplitude and T0 = 36 ps. The MLSE was implemented with an eight-state Viterbi algorithm where a perfect knowledge of the channel response is assumed.
Figures 2 and 3 show the bit error rate (BER) versus OSNR for an optical channel with 100 and 200 km of fiber span, respectively. We present theoretical values obtained from (21), and simulation results of the entire system using both (i) the optimum metrics based on the exact pdf of the received signal (2), and (ii) the approximate metrics defined by (6). Parameter dmin in (21) is found from the Viterbi algorithm by exhaustive search. In all cases, comparisons between the values derived from the theory and simulation confirm the good accuracy of the lower bound (21) presented in this paper.
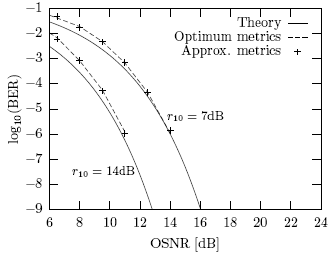
Figure 2: BER versus OSNR for 100 km of fiber. M = 3.

Figure 3: BER versus OSNR for 200 km of fiber. M = 3.
VI. CONCLUSIONS
In this paper, we have introduced a new theoretical performance analysis of lightwave systems in the presence of nonlinear dispersion and ASE noise. Unlike previous contributions, we have derived a simple closed-form analytical expression for the bit error probability. The accuracy of the new theory has been confirmed by comparison with values derived from computer simulations. Finally, although the analysis presented here considers ideal optical/electrical filters (e.g., integrate-and-dump electrical filters), simulation results not presented in this work have shown that the accuracy of the new analysis is also satisfactory for more realistic filters such as, for example, raised cosine optical and five-pole Bessel electrical filters (Bosco et al., 2003; Forestieri, 2000)
1 In our case, each detection error causes exactly one bit error.
REFERENCES
1. Agazzi O. E., and V. Gopinathan, "The impact of non-linearity on electronic dispersion compensation of optical channels", in Proc. of the Optical Fiber Communication Conference and Exhibit (OFC), (2004a). [ Links ]
2. Agazzi O. E., D. E. Crivelli, and H. S. Carrer, "Maximum likelihood sequence estimation in the presence of chromatic and polarization mode dispersion in intensity modulation/direct detection optical channels", in IEEE Proc. of the International Conference on Communications (ICC), 5, 2787-2793, (2004b). [ Links ]
3. Agrawal G. P., Fiber-Optic Communication Systems. Wiley-Interscience, (1997). [ Links ]
4. Bosco G., G. Montrosi, and S. Benedetto, "Soft decoding in optical systems", IEEE Trans. Commun., 51, 1258-1265, (2003). [ Links ]
5. Carrer H. S., D. E. Crivelli, and M. R. Hueda, "Nuevo detector para sistemas de transmisión por fibra óptica", Xo RPIC (Reunión de Procesamiento de la Información y Control), 1, 322-327, (2003). [ Links ]
6. Forestieri E., "Evaluating the error probability in lightwave systems with chromatic dispersion, arbitrary pulse shape and pre-and postdetection filtering", J. Lightwave Technol., 18, 1493-1503, (2000). [ Links ]
7. Haunstein H. F., K. Sticht, A. Dittrich, W. Sauer-Greff, and R. Urbansky, "Design of near optimum electrical equalizers for optical transmission in the presence of PMD", in Proc. of the Optical Fiber Communication Conference and Exhibit (OFC), 3, 558-560, (2001). [ Links ]
8. International Telecommunications Union ITU-T Recommendation G.652, Characteristics of Single-Mode Optical Fibre and Cable, (2003). [ Links ]
9. Lee E. A., and D. G. Messerschmitt, Digital Communication. KAP, second ed, (1988). [ Links ]
10. Marcuse D., "Derivation of analytical expressions for the bit-error probability in lightwave systems with optical amplifiers", J. Lightwave Technol., 8, 1816-1823, (1990). [ Links ]
11. Papoulis A., Probability, Random Variables, and, Stochastic Processes. McGraw-Hill, third ed., (1991). [ Links ]
12. Proakis J. G., Digital Communications. McGraw-Hill, third ed., (1995). [ Links ]
13. Ramaswami R., and K. Sivarajan, Optical Networks: a Practical Perspective. Morgan Kaufmann, (2002). [ Links ]
14. Weiss A. J., "On the performance of electrical equalization in optical fiber transmission systems", IEEE Photon. Technol. Lett., 15, 1225-1227, (2003). [ Links ]
15. Winters J. H., and R. D. Gitlin, "Electrical signal processing techniques in long-haul fiber-optic systems", IEEE Trans. Commun., 38, 1439-1453, (1990). [ Links ]














