Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.35 n.2 Bahía Blanca abr./jun. 2005
Cardiovascular engineering: modelization of ventricular-arterial interaction in systemic and pulmonary circulation
D. Craiem1,2, S. Graf1,2, F. Pessana1,2, J. C. Grignola3, D. Bia3, F. Ginés3 and R. Armentano1,2,3
1 Universidad Favaloro, Av.Belgrano 1723(1093), Ciudad de Buenos Aires, Argentina. Contact: dcraiem@favaloro.edu.ar
2 Universidad Tecnológica Nacional, FRBA, Medrano 951(1179), Ciudad de Buenos Aires, Argentina
3 Universidad de la República, Facultad de Medicina, Gral. Flores 2125(11800), Montevideo, Uruguay
Abstract ¾ The heart pumps pressure and flow signals with relevant amount of frequency components cushioned along the arterial system. A pressure transfer function approach was designed to evaluate the Ventricular-Arterial Interaction. Two transfer functions were calculated relating ventricular to arterial pressure. A frequency response analysis followed the time-domain adaptation. Additionally, a viscoelastic model was proposed to characterize the arterial wall mechanical behavior, using the elastic (E) and viscous (h ) moduli.
Six merino sheep were instrumented and anesthetized. Pressure measurements were registered in both ventricles, in aorta and in the pulmonary artery. Diameters (sonomicrometry) were measured in both arteries.
The frequency transfer function asymptotic negative slope, describing the attenuation within the dynamic range, resulted 5 times greater in aorta (p<0.05), what presents the systemic as a more selective circuit than the pulmonary. E and h resulted higher (p<0.05) in aorta than in the pulmonary artery whereas E/h was similar.
The viscoelastic results might indicate a similar segmental (unit-cell) response in both arteries. The enhanced cushioning ability of the left circuit with respect to the right, might be understood as a more selective vascular filtering system. This filtering performance might be related to the functional length of unit-cell responses along the systemic circulation.
Keywords ¾ Aorta. Pulmonary Artery. Transfer Function. Viscoelasticity.
I. INTRODUCTION
The heart and the arterial system interact in order to provide adequate flow and pressure to peripheral tissues. Whereas the ventricle generates a pulsatile flow, the arterial system is responsible for two main issues (Nichols and O'Rourke, 1998): a) distribution (conducting function); b) filtering or cushioning, supplying constant flow to distal extremes (buffering function).
In order to describe the arterial system as a hydraulic load, the wall mechanical response could be evaluated. Large arteries mechanical response might be described with a viscoelastic model where the inertial term might be neglected (Armentano et al., 1995). The elastic (E) and viscous (h) moduli can be calculated from a pressure-diameter (P-D) loop to asses a simple model of two parallel elements (Cox, 1978). In the first-order model response, the E/h time constant might be adopted to describe the diameter response to a steep pressure (Gamero et al., 2001).
Both the systemic and the pulmonary circuits are based on a pump (the ventricle) and a hydraulic load (the arterial system), each of which generates and receives the same blood volume, respectively. Nevertheless, these circuits exhibit distinctive characteristics regarding their pressure values, effective length (Burattini and Di Carlo, 1988), arterial diameter and compliance, myocardial contractility, cardiac cycle phases (Ginés and Grignola, 2001) and peripheral resistance, among others. This makes it impossible to extrapolate the characteristics of the ventricular-arterial interaction (VAI) from one circuit to the other, making their simultaneous dynamic characterization essential for a proper comparison.
Interactions between the ventricle, as a pump, and the arterial system, as a load, have been previously analyzed by many others (Asanoi et al., 1989; Kass and Kelly, 1992; Kussmaul et al., 1992; Cohen-Solal et al., 1994). Two different approaches have been used. The first method involves pressure-volume loops and static ventricle-arterial elastances (Suga et al., 1973; Sunagawa et al., 1983, 1984; Burkhoff and Sagawa, 1986; De Tombe et al., 1993). The second, concerning impedance concepts, showed to be more solid theoretically but less practical and accurate (Abel, 1971; Sunagawa et al., 1985).
This work deals with VAI in the left and right circulation simultaneously, in steady state. A 3x3 ARMA adaptive model fits the output arterial pressure (AP) and input ventricular pressure (VP) signals in time domain. In addition, a linear function, relating AP to VP is calculated in the frequency domain.
Two transfer functions are obtained. The systemic (Hs=APAo/VPL), relating the aorta pressure to the left VP, and the pulmonary (Hp=APPu/VPR), relating the pulmonary AP to the right VP.
The purposes of this study are: 1) to provide a simple and original approach in the VAI study through AP to VP transfer functions in the frequency domain, both in the systemic and pulmonary circuits, simultaneously; 2) to use these transfer functions to quantify the hydraulic filtering capacity of each one of the circuits; 3) to contrast the systemic and pulmonary VAI with the arterial wall mechanical response related to the hydraulic load.
II. METHODOLOGY
The study was conducted on 6 merino sheep weighing 26±4.5kg (aged 20±2 month). They were anesthetized with intravenous administration of pentobarbital sodium i/v (35 mg/kg) and ventilated with a positive pressure respirator via a cervical tracheotomy. Arterial oxygen and carbon dioxide partial pressures were monitored. Respiratory rate and tidal volume were adjusted to maintain pCO2 at 35-45 mmHg and pH at 7.35-7.4. Arterial pO2 always exceeded 80 mmHg. The heart was exposed by a left thoracotomy, performed at the fourth intercostal space. Four pressure microtransducers (Konigsberg P7, 1200 Hz) were positioned in the left and right ventricles, aorta and in pulmonary artery. In order to calculate the P-D loop, two ultrasonic piezoelectric crystals (3 MHz, 5 mm of diameter) were implanted in aorta and in pulmonary artery, connected to a sonomicrometer (Triton Technology, model l20, l000 Hz). At the end of each experiment, the animal was sacrificed by intravenous injection of potassium chloride under deep barbiturate anesthesia. The surgical and experimental procedures conformed to the Guide for the care and Use of Laboratory Animals publishing by the National Institutes of Health (NIH Pub No86-23, revised 1985).
A. Data Acquisition and Analysis
Pressure signals (VPL, VPR, APAo, APPu) and arterial dimensions (DAo, DPu ) were simultaneously monitored and recorded in real time (200Hz sample rate) after a 50Hz low-pass filter process.
A two-parallel-element model was adopted (Kelvin-Voigt viscoelastic model) to characterize the arterial wall. Accordingly, total pressure developed by the wall to resist stretching can be separated into an elastic and a viscous pressure component (Armentano et al., 1995). As viscous pressure is proportional to the first derivative of the artery diameter, the elastic pressure component can be obtained as:
 | , (1) |
where h is the arterial wall viscous modulus. To separate the purely elastic wall properties, the viscous term must be subtracted from the total pulmonary pressure, finding the optimal value through the hysteresis loop disappearance criteria (Armentano et al., 1995). The resulting elastic behaviour in the pressure-diameter loop can be used to calculate E as the slope of a linear regression fit to the diastolic phase at mean pressure.
To analyze the temporal response of the arterial wall, as in a Kelvin-Voigt model, the following pressure-diameter equation, using (1) and the calculated E, is proposed
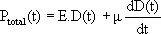 | (2) |
where the h/E time constant would characterize the temporal exponential diameter response to a steep pressure increase (creep):

An adaptive model (ARMA 3x3) was employed to obtain the systemic (Hs) and pulmonary (Hp) transfer functions (Fig. 1). Ten consecutives stable pressures cycles were selected for each adaptation in the time domain. Using the 7 fitted coefficients (a0-3, b1-3), Hs and Hp frequency domain functions were calculated and approximated through an asymptotic Bode diagram. The filtering selectivity was characterized by the descending slope, within the band of interest (1-10Hz). In addition, the transference values in zero frequency (Hs(0) and Hp(0)) were calculated. Mean squared error was calculated for each adaptation to quantify the model-system adjustment.
Statistical results are expressed as mean ± SD. A paired t-student test with a p<0.05 significance level was adopted.


Fig. 1. Top: An Example of pulmonary arterial time adaptation to calculate the pulmonary transfer function (Hp) using a 3x3 ARMA model. Bottom: Adaptive model diagram.
The normalized mean squared error (MSE) between the arterial pressure and the calculated arterial pressure was evaluated during a stable cycle of N points,

and it was adopted to evaluate the adaptation robustness of the adaptive process.
III. RESULTS
A. Hemodynamic Parameters
All pressure values are summarized in Table 1. Pulse pressure (PP) to systolic pressure ratio in the systemic and pulmonary circuits were 0.37±0.09 and 0.5±0.17, respectively. Heart rate was 1.8±0.5 Hz.
TABLE I: HEMODYNAMIC VALUES

VP: Ventricular pressure; AP: Arterial pressure; L: left; R: right; Sys: systole; Dia: diastole; Ao: aorta; Pu: pulmonary; * p<0.01 (unpaired t test)
B. Ventricular-Arterial Interaction
Twelve transfer functions were calculated (6 systemic and 6 pulmonary) in the frequency domain. Systemic representative (modulus) values resulted: Hs(0Hz)= 4.2±2dB, Hs(1Hz)=-9±2.4dB and Hs(1-10Hz)=-14±6dB/dec. For the pulmonary function Hp(0Hz)=4.1±1.3dB, Hp(1Hz)=-9± 2.1dB and Hp(1-10Hz)=-3± 2dB/dec (p< 0.05), with respect to the systemic slope. Pulmonary and systemic normalized MSE resulted 0.3±0.1% and 0.6±0.1%, respectively. Modulus of the 12 transfer functions are showed in Fig.2.


Fig. 2. Pulmonary and systemic transfer function modulus. Logarithmic frequency scale was employed and asymptotic Bode approximation in the 1-10HZ band is dotted lined.
C. Arterial Mechanical Response
The elastic and viscous moduli were higher (p<0.05) in aorta, although the h/E ratio was similar for both arteries.
TABLE II: VISCOELASTIC VALUES

Pu: pulmonary; D: Diameter, E: Elastic modulus, h : Viscous modulus, * p<0.05 (t-test with respect to Aorta)
IV. DISCUSSION
The present work presents transfer functions in the frequency domain that are proposed to study ventricular-arterial interaction (VAI) in stable pressure conditions. They provide qualitative and quantitative information about the efficiency of the hydraulic filtering that take place in both, the systemic and pulmonary, circulation circuits. Traditional methods for evaluating this interaction involve impedance matching and pressure-volume loops, whereas transfer functions use a simple method and do not require flow measurements.
The ventricle is an intermittent pump. Pulsatile pressure and flow must be cushioned in order to reach the arterioles/capillaries with the minimum pulsatile components. Both pulmonary and systemic circuits behave as low-pass hydraulic filters, as can be confirmed with the transfer function frequency response (Fig. 2).
Arterial pressure and ventricle pressure were considered as output and input of a linear system, respectively. This system is fitted with an adaptive ARMA 3x3 model in the time domain. The model order was adopted following a previous work methodology of our group (Gamero et al., 2001) where viscoelastic elements were characterized showing a proper adjustment. Once the 7 model coefficients (a0-3,b1-3) were fixed for each circuit, the transfer function in the frequency domain was calculated. Using a time domain adaptive model, the frequency response can be found as a continuous function in contrast with traditional Fourier methods, where high frequency noise is a limiting factor. A better adaptation was found for the pulmonary circuit. This is confirmed graphically and numerically, using MSE criteria. This difference may be due to less definite reflected wave effect, making the pulmonary AP signal simpler to adapt with a linear model. Consequently, a small offset remained in the mean final value of the systemic response.
The slope of the descending frequency response in the transition band is usually associated to filter selectivity. The selectivity was characterized by the descending slope within the band of interest (1-10Hz), using an asymptotic Bode diagram to simplify the comparisons. The HR was 1.8±0.5 Hz, allowing the fundamental and 5 main components to be included in this band of interest.
The systemic circuit resulted 5 times more selective than the pulmonary. Systemic circulation shows an enhanced selectivity in accordance with an improved filtering function. This is highlighted in Fig. 2 where the doted lines match the values of the slope of Hs and its pulmonary counterpart Hp.
Moreover, this filtering idea can be inferred from pulse pressure (PP) to systolic pressure ratio. The systolic pressure is associated with ventricle pressure and PP to arterial pressure. Whereas the relationship between the systemic PP to systolic VPL is approximately 37%, pulmonary PP to systolic VPR is around 50%. Finally, the systolic frequency response can be calculated using Abel's results (Abel, 1971), coherent with ours.
The values of the transfer function for frequencies approaching zero are related to the ratio between arterial and ventricular mean pressures. As expected, the gain of mean pressures in the systemic circuit was somewhat higher than the pulmonary. Mean aortic pressure is 1.6 times mean pulmonary AP while mean VPL doubles the mean VPR.
As impedance concepts, transfer function applications rely on linearity assumption. In spite of the actual non-linearity in the pressure signals, the temporal adaptation showed a concise robustness. In addition, all the pressure signals were acquired during steady states, avoiding non-linear mechanisms to influence the pressure response. Spectral coherence performed over ventricle and arterial pressures confirmed a strong linear relation until frequencies near 40Hz (data not showed).
The low-pass filtering effect might be associated with the arterial cushioning function. To assess arterial mechanical response, a two parallel element Kelvin-Voigt model was adopted. Using the P-D loop E and h can be calculated (Armentano et al., 1995). The inertial behavior might be neglected following previous works considerations (Armentano et al., 1995; Gamero et al., 2001). The elastic modulus was higher in Ao with respect to the pulmonary artery, confirming its stiffer condition. Additionally, viscous modulus resulted higher in Ao, suggesting elevated energy dissipation in Ao with respect to the pulmonary. A higher smooth muscle presence could contribute to this difference. In a first order model, the time constant h/E describes the diameter response following a steep pressure in a segmental perspective. A large h/E value is associated with a slow response and an enhanced cushioning function. In both arteries h/E was similar, suggesting that the studied segments might have a similar mechanical response. The arterial load might be described as a sequence of unit-cells characterized with viscoelastic model parameters. Although it is well known that the structure of the arterial wall changes as we move away from the heart, the buffering function is mostly concentrated in the proximal section's compliance.
The h/E ratio resulted similar in both arteries but the systemic selectivity was higher in the systemic circuit, according to slopes of the transfer functions. As the systemic circuit is a longer conduit, with respect to the short pulmonary path, the mechanical cushioning ability might be associated with a longer sequence of these conceptual unit-cells.
V. CONCLUSION
This work deals with transfer function to characterize the VAI. The transfer function slope, within the dynamic frequency range, is a VAI parameter that describes the attenuating effect that smoothes the pulsatility the ventricle pumps into the arterial system and that might impair vascular performance. The slopes resulted 5 times steeper in the systemic circuit compared with the pulmonary circuit. The results of the viscoelastic model, employed to characterize the Ao and the pulmonary artery, indicate a similar segmental (unit-cell) response. The enhanced cushioning ability of the left circuit with respect to the right, might be understood as a more selective vascular system. This filtering performance might be related to a longer sequence of unit-cells along the systemic circulation.
Although this work was conducted in sheep, the ventricle and arterial pressure might be hypothetically applied invasively in cardiac patients by means of a two-tip pressure catheter, and the results might be extrapolated accordingly to evaluate their VAI.
ACKNOWLEDGEMENTS
This work was performed within a cooperation agreement between Universidad de la República (Uruguay)-Universidad Favaloro (Argentina), and it was partially supported by Fondo Clemente Estable -Dinacyt No8284.
REFERENCES
1. Abel F., "Fourier analysis of left ventricular performance. Eval. of impedance matching", Circ.Res., 28, 119-135 (1971). [ Links ]
2. Armentano R. L., J. G. Barra, J. Levenson, A. Simon, and R. H. Pichel, "Arterial wall mechanics in conscious dogs: assessment of viscous, inertial, and elastic moduli to characterize the aortic wall behavior", Circ. Res., 76, 468-478 (1995). [ Links ]
3. Asanoi H., Sh. Sasayama, and T. Kameyama, "Ventriculo-arterial coupling in normal and failing heart in humans" Circ. Res., 65, 483-493, (1989). [ Links ]
4. Burattini R., and S. Di Carlo, "Effective length of the arterial circulation determined in the dog by aid of a model of the systemic input impedance", IEEE Trans. Biomed. Eng., 35, 53-61, (1988). [ Links ]
5. Burkhoff D., and K. Sagawa, "Ventricular efficiency predicted an analytical model", Am. J. Physiol., 250, R1021-R1027, (1986). [ Links ]
6. Cohen-Solal A., B. Caviezel, D. Himbert, and R. Gourgon, "Left ventricular arterial coupling in systemic hypertension: analysis by means of arterial effective and left ventricular elastances", J. Hypertension, 12, 591-600, (1994). [ Links ]
7. Cox R. H., "Passive mechanics and connective tissue composition of canine arteries", Am. J. Physiol., 234, H533-H541, (1978). [ Links ]
8. De Tombe P. P., S. Jones, D. Burkhoff, W. C. Hunter, and D. A. Kass, "Ventricular stroke work and efficiency both remain nearly optimal despite altered vascular loading", Am. J. Physiol., 264, H1817-H1824, (1993). [ Links ]
9. Gamero L., R. L. Armentano, J. G. Barra, A. Simon, and J. Levenson, "Identification of arterial wall dynamics in concious dogs", Exp. Phys., 86.4, 519-528, (2001). [ Links ]
10. Ginés F., and J. C. Grignola, "Sincronización de la contracción del ventrículo derecho frente un aumento agudo de su poscarga. "Izquierdización" el comportamiento mecánico del ventrículo derecho", Rev. Esp. Cardiol. 54, 973-980, (2001). [ Links ]
11. Kass D. A., and R. P. Kelly, "Ventricle-arterial coupling: concepts, assumptions and applications", Ann. Biom. Eng., 20, 41-62, (1992). [ Links ]
12. Kussmaul W. G., A. Noordergraaf, and W. K. Laskey, "Right ventricular - pulmonary arterial interaction", Ann. Biom. Eng., 20, 63-80, (1992). [ Links ]
13. Nichols W. W., and M. F. O'Rourke, McDonald's Blood Flow in Arteries, fourth edition, Ed. Arnold, (1998). [ Links ]
14. Suga H., K. Sagawa, and A. Shoukas, "Load independence of the instantaneous pressure-volume ratio of the canine left ventricle and effects of epinephrine and heart rate on the ratio", Circ. Res., 32, 314-322, (1973). [ Links ]
15. Sunagawa K., W. L. Maughan, D. Burkhoff, and K. Sagawa, "Left ventricular interaction with arterial load studied in isolated canine ventricle", Am. J. Physiol., 245, H773-H780, (1983). [ Links ]
16. Sunagawa K., K. Sagawa, and W. L. Maughan, "Ventricular interaction with the loading system", Ann. Biom. Eng., 12, 163-189, (1984). [ Links ]
17. Sunagawa K., W. L. Maughan, and K. Sagawa, "Optimal arterial resistance for the maximal stroke work studied in isolated canine left ventricle" Circ. Res., 56, 586-595, (1985). [ Links ]














