A new approach to distillation of continuous mixtures: modelling and simulation

P. A. D. Jácome¹, F. C. Peixoto², G. M. Platt³ and V. R. R. Ahón⁴

¹ Instituto Politécnico, Universidade do Estado do Rio de Janeiro, Nova Friburgo/RJ, Brasil
pjacome@iprj.uerj.br
² Depto. Engenharia Química, Instituto Militar de Engenharia , Rio de Janeiro/RJ , Brasil
fpeixoto@ime.eb.br
³ Instituto Politécnico, Universidade do Estado do Rio de Janeiro, Nova Friburgo/RJ, Brasil
gmplatt@iprj.uerj.br
⁴ Escola de Química, Universidade Federal do Rio de Janeiro, Rio de Janeiro/RJ, Brasil
ruiz@peq.coppe.ufrj.br

Abstract — Continuous Mixtures are mixtures of so many components that is no longer useful to distinguish among chemical species. Instead, an index is chosen to characterize each molecule, such as carbon atoms in each substructure, chromatographic retention time or normal boiling point and the continuity of this index is admitted. The present work aims the mathematical formulation and the simulation of a distillation column in which a continuous mixture is fed. This is performed with the assumption of a mixture of linear paraffins, in which ideal mixture hypothesis in both liquid and gas phases are reasonable. A quadrature method is employed to calculate the integrals which turns the functional-algebraic problem into a numerical one.

Keywords — Continuous Mixtures. Distillation. Quadrature Method.

I. INTRODUCTION

The concept of continuity of a given mixture is applied whenever that mixture is so complex that it is no longer worthwhile to distinguish among individual chemical species; instead, an index (such as number of carbon atoms, boiling point or chromatographic retention time) is chosen to characterize each component and the continuity of the index is assumed. Mole fraction x_i of species A_i is replaced by f (x)dx,the molar fraction of material with an index in the (x, x + dx) interval. Function f (x) is known as the mixture distribution function (DF), where x is the continuous index of the mixture. In some cases, more than one index must be used to completely characterize the continuum of species, which increases the mathematical complexity of any phenomena described with a continuous approach.

Distribution functions exhibit an obvious normalization condition given by:

. (1)

Vapor-liquid equilibria (VLE) calculations for complex mixtures has been traditionally accessed through a Pseudo-Component Method, that is basically a "lumping" approach in which key components are chosen to fully characterize the whole mixture. In this way, a simple modelling procedure can be adopted, but results are highly dependent on the choice of the set of pseudo-components (Chachamovitz, 1993).

The development of the continuous thermodynamics had shown great advantages in many aspects (Peixoto et al., 2000). When applying continuous thermodynamics, a critical point is the choice of the continuous index. Some authors chose a natural identification variable, such as molecular weight or boiling point (Du and Mansoori, 1986; Cotterman and Prausnitz, 1985). However, it is sometimes difficult to relate such indices with other thermodynamic properties, especially equations of state (EOS) parameters, and fitted polynomials have been employed (Cotterman et al., 1985).

The simulation of distillation columns using a continuous approach was previously addressed by Kehlen Rätzsch (1987) and Rätzsch et al. (1989). However, these authors employ boiling-point temperature as the continuous index, differing essentially of this work.

This work aims the modelling of distillation columns in which a continuous mixture is fed, the most important examples being paraffinic fractions of petroleum. The well-established Quadrature Method (Cotterman and Prausnitz, 1985; Peixoto et al., 2000) is employed for solving the problem. This method was considered the most suitable, once it does not show the error in material balance of the Method of Moments (Cotterman et al., 1985). The VLE is accessed through its most simple form, once paraffinic mixtures are one of the most common examples of mixture with ideal behavior. However, the approach presented here can be easily extended for non-ideal vapor phases (as used in Peixoto et al., 2000) and liquid phases (using a group contribution method for estimation of activity coefficients).

II. MATHEMATICAL MODELLING

A. Continuous Mixtures Thermodynamics

As mentioned in Cotterman et al. (1985), the VLE for continuous mixtures can be written in a way similar to the discrete case:

Y(x)f_V(x, T, P, Y(x)) = X(x)f_L(x, T, P, X(x)), (2)

where X(x)and Y(x) stands for the liquid and vapor DF respectively and f(x) stands for the fugacity coefficient of the component with index x;subscripts V and L stand for vapor and liquid phases, respectively; T is the temperature in K and P the pressure in Pa. As already mentioned, the present work employs ideal assumptions and Eq. (2) turns into:

, (3)

where P^sat(x, T) stands for the vapor pressure of the molecule with index x at temperature T . Once again, the analogy with the discrete case can be seen.

As it can be seen, those equations demand a method to predict P^sat(x, T) as a function of the continuous vector parameter x. This can be carried out with well-established group contribution methods, as Joback (1984) predictions for normal boiling point (T_b)and critical coordinates (T_c and P_c). If x is the number of groups in the molecular structure, the expressions are:

	, (4)
	, (5)
	, (6)

where N_a stands for the total number of atoms in molecule. All summations are performed over the groups present on the molecule, accounting individual contributions of each of increments ΔT_b,ΔT_c and ΔP_c.

Equations (4) to (6) are required for the vapor pressure prediction, which can be performed with the following equation (Gómez-Nieto and Thodos, 1978):

, (7)

where

	, (8)
	, (9)
	, (10)
	, (11)
	, (12)
φ = τs + χξ	, (13)

The equation of Gómez-Nieto and Thodos (1978) was validated comparing the calculated vapor pressures with corresponding values reported in the literature, for 113 substances. The average percent deviation was found to be 0.97 % (for more details, see Gómez-Nieto and Thodos, 1978).

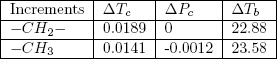
Table 1 below provides the necessary elements for the calculation of Eqs. (4) to (6) for linear paraffins in terms of each incremental substructure in a linear alkane molecule:

Table 1 - Group contributions

Finally, for a linear paraffin, Joback's vector to account for incremental substructure in terms of x is given by:

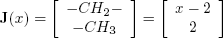. (14)

Summations in Eqs. (4), (5) and (6) are then performed as follows:

	(15)
	, (16)
	. (17)

However, Joback predictions for normal boiling point and critical temperatures are not accurate. The values predicted by Joback method are considerably higher than the experimental ones for a carbon number higher than 13. Thus, in this work, we opted by the expression of Cordes and Rarey (2002) for boiling point temperatures, as follows:

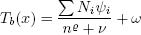, (18)

where = 0.6713, ν = 1.4442, ω = 59.344 (adjustable parameters), N_i is the number of groups of type i, ψ_i is the group contribution of group i and n is the number of atoms in the molecule (except hydrogen). For a linear alkane, it is clear that n = x,since we have only carbon and hydrogen atoms. For a -CH₃ group, ψ = 188.555, and for a -CH₂-group, we have ψ = 250.119 (Cordes and Rarey, 2002).

For prediction of critical temperatures, the Equation of Teja et al. (1990) was used:

(19)

where = -0.160864 + 0.9225x

One can notice that, even not using Joback's group contribution method, the equations of Cordes and Rarey (2002) and Teja et al. (1990) are also based in a group contribution approach -which can be used in a continuous context.

B. Constant Molar Overflow Assumptions and Resulting System of Equations

Consider the following equilibrium stage of a continuous distillation column (with descendent enumeration):

Figure 1: Equilibrium Stage j at temperature T_j and pressure P_j.

In Fig. 1, F, V, L, W and U represent, respectively, molar flow rates of feed, vapor, liquid, and sidestreams of vapor and liquid (in mol/s); β_j represents the thermal condition of feed; subscripts represent individual equilibrium stages (top condenser being the first and reboiler the last of them). The column operates with partial condenser and partial reboiler and has N equilibrium stages. Gaseous streams DFs are denoted by Y(x) - with the corresponding subscript - and liquid streams are characterized by a DF denoted by X(x), while the feed is characterized by Z(x). The feed stream DF was chosen to be a gamma distribution with and η parameters:

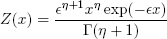. (20)

This DF obeys the normalization constrain represented by Eq. (1) and is able to emulate a discrete case where a single molecule is present:

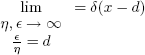, (21)

where δ is the Delta Dirac function. Eventually, multi-modal distributions are needed, and can be described by the following equation:

, (22)

where , in order to maintain the normalization condition.

Any stage (including condenser and reboiler) can be described by the MESH equations, as follows:

FjZj(x) + Vj+1Yj+1(x) + Lj-1Xj-1(x) - (Vj + Wj)Yj(x) - (Lj + Uj)Xj(x) = 0	, (23)
Yj(x) = k(x,T)Xj(x)	, (24)
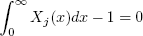	, (25)
	, (26)
	. (27)

The constant molar overflow (CMO) assumptions (also called McCabe-Thiele approximations) are suitable in distillation problems with close-boiling components, in order to avoid the need of energy balances. In continuous sense, CMO assumptions are a consequence of the following forms for the saturation enthalpies for liquid and vapor phases (see Appendix 1):

	, (28)
	, (29)

where the superscript sat refers to a saturation condition. The difference A-a represents the molar heat of vaporization of the mixture (which is considered constant). Within this approximation, it can be shown that the enthalpy for a feed stream F is given by:

, (30)

where the thermal condition of F is expressed by the vaporized fraction . As consequences of Eqs. (28)-(30), we have:

Vj+1 = Vj + Wj - Fjβj - j/λ	, (31)
Lj = Lj-1 - Uj + Fj(1 - βj) - j/λ	, (32)

Equations (31) and (32) can be verified using (28)-(30) into Eq. (27) and considering the material balance equation [Eq. (23)].

III. NUMERICAL PROCEDURE

If CMO assumptions are valid for a thermodynamic system, Eqs. (31) and (32) can be used instead of, for instance, Eqs. (25) and (27). It is possible to note that Eqs. (31) and (32) represent a linear system of equations that must be solved for V_j(j = 1, ..., N), L_j(j = 1, ..., N) and _j(j = 1, ..., N). We consider that all side-streams flow rates are specified. This system has 3N variables and 2N equations; then, if one specify _j(j = 2, ..., N - 1), external reflux ratio (R)and distillate flow rate (V₁), as follows:

L1 - R(V1 + U1spec + W1spec) = 0,	(33)
V1 - V1spec = 0,	(34)

the number of degrees of freedom is zero.

Thus, all molar flow rates in the entire column are determined (and heat duties in condenser and re-boiler), and now the problem consists only on determination of DFs for gaseous and liquid streams and temperatures in each stage.

Once integrals as Eq. (26) are accessed through some numerical procedure like:

, (35)

where x_i and w_i are, respectively, n collocation points and weights of the procedure, one can easily see that DFs are only calculated on some particular points (Y); if information additional is needed, an interpolation can be conducted. Therefore, if we denote by X_j and Y_j the collocated DFs of stage j, system (23), (24) and (26) becomes:

FjZj + Vj+1Yj+1 + Lj-1Xj-1 -(Vj +Wj)Yj - (Lj + Uj)Xj = 0,	, (36)
	, (37)
wtYj - 1 = 0.	(38)

In Eq. (37), diag refers to a diagonal matrix. The system of equations (23), (24) and (26) is completely analogous to the one devoted to the simulation of a column with n discrete components (in this case w_i = 1 for every i). Even though for many years distillation of complex mixtures was accessed through the usage of pseudo-components, the choice of such species was usually based on chemical and physical properties which lead to poor results. With the present approach, the criteria is purely mathematical (and aims DFs complete calculation) and properties can be completely recovered at any time. The system is solved for vapor and liquid compositions and temperatures only in collocation points, using a simultaneous-correction procedure (Naphtali and Sandholm, 1971), as usually is done in distillation problems.

IV. NUMERICAL RESULTS

Simulation results are obtained for a feedstock characterized as represented in Table 2 (Wojciechowski, 1996). Adjusting this characterization for a gamma distribution [Eq. (20)], using a Maximum Likelihood procedure, the parameters obtained are = 0.9885 and η = 10.0022 (Peixoto, 1996). Table 3 presents the column specifications. The column operates with a partial condenser and a partial reboiler and the feed is considered saturated liquid.

Table 2 - Feed characterization

Table 3 - Column Specifications

In order to validate the results obtained using the continuous approach, a discrete simulation was performed using PRO/II™ Simulator (licensed by Escola de Química/UFRJ)¹. In this simulation, we consider ideal vapor and liquid phase (which is reasonable, considering a mixture of linear paraffins). However, the assumption of constant molar overflow was not used. Fig. 2 presents the composition of the distillate product -calculated using continuous modelling and the simulator PRO/II. For the discrete simulation (using the PRO/II simulator), DFs refer to the molar fractions of each component. The same objects are plotted for the bottom product in Fig. 3. In these figures, the index x refers to the number of carbon atoms in the alkane. The temperature profile in the column, using both approaches, is presented in Fig. 4.

A good agreement between continuous and discrete results can be observed, indicating the capability of the proposed methodology to predict the behavior of complex mixtures (containing very many components), in a separation equipment. We consider that the differences in temperature profiles are, essentially, consequences of using group contribution correlations for normal boiling points and critical coordinates, since the equation of Gómez-Nieto and Thodos can predict, with low deviations, vapor pressures for linear alkanes. Besides, the CMO assumption (used in our continuous approach) is a good approximation for this kind of mixture.

Figure 2: Compositions for distillate product.

Figure 3: Compositions for bottom product.

Figure 4: Temperature Profile.

V. CONCLUSIONS

This work aims the modelling of distillation columns, in which a continuous mixture is fed, using a choice for the continuous index not previously used for that purpose. We illustrate some advantages of our choice with respect to choices (see, for example, Kehlen and Rätzsch, 1987; Rätzsch et al., 1989) previously used in the literature.

A steady-state simulator was implemented, based on a simultaneous-correction method for the solution of the system of non-linear equations (in the collocation points) for compositions and temperatures in each tray of the column. Calculations of flow rates in each section of the equipment were done solving a linear system of equations, which is a consequence of decoupling of material and energy balances generated by CMO assumptions.

Results are presented for a feedstock characterized by Wojciechowski (1996), and illustrate the split obtained in distillate and bottom products. The results were compared with the discrete approach, using PRO/II simulator (which does not consider CMO in each section of the column), and a good agreement was obtained.

As discussed previously, for many years the distillation of complex mixtures was accessed through the usage of pseudo-components, and the choice of such species was usually based on chemical and physical properties which lead to poor results. With the present approach, the criterion is purely mathematical (and aims DFs complete calculation) and properties of top and bottom products of the column (and even in a particular tray in the column) can be completely recovered at any time.

Nomenclature

	Heat duty
J(x)	Joback's vector
A	Constant in Eq.(28)
a	Constant in Eq.(29)
b(x)	DF used in CMO assumptions
Ci	Weights in Eq. (22)
cp(x)	Molar heat capacity DF for liquids
F	Feed molar flow rate
f(x)	Distribution function
H	Molar enthalpy
k(x, T)	Vapor-liquid equilibrium ratio Liquid molar flow rate
m	ParemeterdefinedinEq. (9)
MESH	Material balance, Equilibrium, Summation and Energy balance equations
Na	Number of atoms in a molecule
Ni	Number of groups of type i
P	Pressure (Pa)
Psat	Vapor pressure
Pc(x)	Critical pressure
PR	Reduced pressure
R	External reflux ration (top)
s	Parameter defined in Eq. (10)
spec	Specified Variable
T	Temperature (Kelvin)
Tb(x)	Normal boiling temperature
Tc(x)	Critical temperature
TR	Reduced Temperature
TRb	Reduced normal boiling temperature,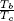
U	Liquid sidestream
V	Vapor molar flow rate
W	Vapor sidestream
wi	Weights of quadrature
x	Continuous index
X(x)	Liquid DF
Y(x)	Vapor DF
Z(x)	Feed DF
diag	Diagonal matrix
β	Thermal condition of the feed
χ	Parameter defined in Eq. (12)
ΔPc	Group Contribution (Joback Method)
ΔTb	Group Contribution (Joback Method)
ΔTc	Group Contribution (Joback Method)
δ	Delta Dirac function
	Parameter of gamma distribution
η	Parameter of gamma distribution
η(x)	Enthalpy of formation DF
Γ	Gamma function
γ	Parameter of Eq. (40)
λ	Molar heat of vaporization
ν	Parameter of Eq. (18)
ω	Parameter of Eq. (18)
f(x)	Fugacity coefficient DF
ψi	Group contribution of group i [Eq. (18)]
τ	Parameter defined in Eq. (11)
θ	Parameter of Eq. (42)
φ	Parameter defined in Eq. (13)
	Parameter of Eq. (18)
	Parameter of Eq. (19)
ξ	ParemeterdefinedinEq. (8)

APPENDIX 1 - SATURATION ENTHALPIES FOR VAPOR AND LIQUID PHASES UNDER CMO ASSUMPTIONS

Suppose that molar enthalpy of the liquid phase can be represented by:

, (39)

where η(x) represents the enthalpy of formation DF at temperature T₀ and pressure P, c_p(x) is the molar heat capacity DF for liquids. The liquid phase can be described as an ideal phase. It is assumed that saturation locus of bubble temperatures can be represented by (under constant pressure):

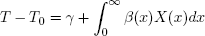. (40)

Thus, saturation enthalpy can be expressed as:

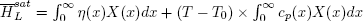(41)

Defining θ as follows:

. (42)

Eq. (41) can be wrote as:

(43)

Thus:

	(44)
	(45)

where a = γθ and b(x)= θβ(x)+ η(x). A similar deduction can be conducted in order to obtain Eq. (28).

---

¹PRO/II is a trademark of Invensys plc., its subsidiaries and affiliated companies.

ACKNOWLEDGMENTS
The authors gratefully acknowledge the financial support of FAPERJ and CNPq for this research.

REFERENCES
1. Chachamovitz, J. C. "Simulação de Processos de Separação de Misturas Semicontínuas", M.Sc. Thesis (in portuguese), PEQ/COPPE, Universidade Federal do Rio de Janeiro, Rio de Janeiro (1993).         [ Links ]
2. Cordes, W. and J. Rarey, "A New Method for the Estimation of the Normal Boiling Point of Non-electrolyte Organic Compounds", Fluid Phase Equilibria 201, 409-433 (2002).         [ Links ]
3. Cotterman, R. L., R. Bender and J. M. Prausnitz, "Phase Equilibria for Mixtures Containing Very Many Components. Development and Application of Continuous Thermodynamics for Chemical Process Design", Ind. Eng. Chem. Proc. Des. Dev. 24, 194 (1985).         [ Links ]
4. Cotterman, R. L. and J. M. Prausnitz,"Flash Calculations for Continuous or Semicontinuous Mixtures Using an Equation of State", Ind. Eng. Chem. Proc. Des. Dev. 24, 434 (1985).         [ Links ]
5. Du, P. C. and G. A. Mansoori, "Phase equilibrium computational algorithms of continuous mixtures", Fluid Phase Equilibria 30, 57-64 (1986).         [ Links ]
6. Gómez-Nieto, M. and G. Thodos, "Generalized Vapor Pressure Equation for Nonpolar Substances", Ind. Eng. Chem. Fundam. 17, 45-51 (1978).         [ Links ]
7. Joback, K. G., "A Unified Approach to Physical Property Estimation Using Multivariate Statistical Techniques", M.Sc. Thesis, MIT, Cambridge, Massachussets (1984).         [ Links ]
8. Kehlen, H. and M. T. Rätzsch, "Complex Multicomponent Distillation Calculations by Continuous Thermodynamics", Chemical Engineering Science 42, 221-232 (1987).         [ Links ]
9. Naphtali, L. M. and D. P. Sandholm, "Multicomponent Separation Calculations by Linearization", AIChE Journal 17, 148-153 (1971).         [ Links ]
10. Peixoto, F. C., "Modelagem e Estimação de Parâmetros em Misturas Contínuas com Reações Químicas", M.Sc. Thesis (in portuguese), TPQB/EQ, Universidade Federal do Rio de Janeiro, Rio de Janeiro (1996).         [ Links ]
11. Peixoto, F. C., G. M. Platt and F. L. P. Pessôa, "Vapor-Liquid equilibria of multi-indexed continuous mixtures using an equation of state and group contribution methods", Chemical Engineering Journal 77, 179-187 (2000).         [ Links ]
12. Rätzsch, M. T., H. Kehlen and J. Schumann, "Computer Simulation of Complex Multicomponent Hydrocarbon Distillation by Continuous Thermodynamics", Fluid Phase Equilibria 51, 133-146 (1989).         [ Links ]
13. Teja, A. S., D. J. Lee, D. Rosenthal and M. Anselme, "Correlation of the Critical Properties of Alkanes and Alkanols", Fluid Phase Equilibria 56, 153-169, (1990).         [ Links ]
14. Wojciechowski, B. W., Personal Communication to F. C. Peixoto (1996).         [ Links ]