Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.35 n.4 Bahía Blanca oct./dic. 2005
About the turbulent scale dependent response of reflexed airfoils
J. S. Delnero, J. Colman, U. Boldes, M. Martinez, J. Marañón di Leo and F. A. Bacchi
delnero@ing.unlp.edu.ar; jcolman@ing.unlp.edu.ar; uboldes@ing.unlp.edu.ar;
mmartinezk@ing.unlp.edu.ar; jmaranon@ing.unlp.edu.ar; fbacchi@ing.unlp.edu.ar
Laboratorio de Capa Límite y Fluidodinámica Ambiental, Departamento de Aeronáutica,
Facultad de Ingeniería, Universidad Nacional de La Plata,
Calle 48 y 116, La Plata (1900), Argentina
laclyfa@ing.unlp.edu.ar
Abstract — Boundary layer wind tunnel experiments have been conducted to explore differences in the aerodynamic behavior of two autostable or reflexed airfoils, with different positive camber submitted to three different incoming flows with the same mean velocity but with different turbulence characteristics.
The variations of lift and drag coefficients due to the path of turbulent structures with different scales are presented.
The experiments were performed at a mean speed of 10 m/sec, corresponding to a Reynolds Number of 205000.
Keywords — Aerodynamics. Turbulence. Low Reynolds Number Airfoils.
I. INTRODUCTION
Standard airfoil data is typically described in terms of steady mean velocities, without a characterization of the turbulent eddies immersed in the natural wind (Bertin and Smith, 1998).
Very different instantaneous local winds with varying incidence and strength act on a wing flying at low height through the atmospheric surface layer.
These velocity fluctuations are caused by the different flow patterns of passing eddies with diverse shapes, dimensions and intensities, embedded in the atmosphere (Hinze, 1975).
These vortex structures are induced by the flow deviations, and velocity variations induced by plants, buildings, different soil roughness, topographic features, density, and temperature gradients.
When a turbulent structure interacts with a wing, flying at constant velocity and angle of attack, the flow becomes nonstationary originating an unsteady pressure field around the wing generating fluctuant lift and drag as well as broadband noise.
The instantaneous angle of attack variations generated by a passing eddy may produce upwash, downwash, stream aligned forward, backward and transversal fluctuations causing unsteady lift and drag. It seems reasonable to conjecture that the aerodynamic forces on a wing submitted to turbulence with prevailing large-scale eddies, behave different from those corresponding to the effects of small scale eddies.
Since nearly 1930, the interaction of turbulence with lifting airfoils has involved important aerodynamic research. Early studies began considering thin plates as airfoils embedded in steady irrotational incompressible flow. Sears (1941) analyzed the unsteady lift and moment of ideal thin flat plates with no angle of attack, flying through irrotational flow at constant velocity submitted to an oncoming sinusoidal vortical perturbation altering the velocity field.
The sinusoidal perturbation used by Sears could be interpreted as an early approach to turbulent structure pattern consideration.
Liepmann (1955) developed a technique considering the frequency spectrum of the incoming turbulence, and Ribner (1956) improved the methodology by including the complete three dimensional turbulence spectrum.
Further research included thickness effects like stagnation point wandering due to turbulence induced angle of attack variations (Morfey, 1970).
McKeough and Graham (1980) considered the distortion effects of a passing turbulent eddy due to the flow pattern of an airfoil by means of the rapid distortion theory.
McKeough and Graham (1980) performed experiments on a NACA 0015 airfoil submitted to grid generated turbulence, measuring the fluctuating lift.
Scott and Atassi (1995) presented a numerical simulation for subsonic flows, with convected three-dimensional gusts.
Despite the different theories about the interaction of turbulence with wings, the experimental research about this issue was infrequent.
II. METHODS
The objectives of the present experiments were concentrated in getting experimental aerodynamic data about the influence of camber in the behavior of airplanes with reflexed airfoils submitted to two flows with different turbulence scales. In reflexed airfoils lift force is placed ahead of the weight force, generating a positive pitching moment contribution (Mc Cormick, 1995). These types of airfoils are often used in flying wing and tailless airplane configurations (Horten and Horten, 1943).

Fig. 1 - R-A and R-B airfoils
Two different airfoils (Fig. 1) called from now on R-A and R-B, were tested. The wings were mounted in the wind tunnel as shown in Fig. 2. The two profiles exhibited different maximum positive and negative cambers calculated to obtain the same resulting airfoil moment coefficient.

Fig. 2 – Wind Tunnel Setup (wing and aerodynamic balance arrangement)
The different maximum positive and negative (reflex) cambers in percentage of chord length were 0.03 and 0.05 for the R-A airfoil and 0.035 and 0.01 for the R-B. airfoil. The chord locations of the maximum positive and reflex cambers were the same for both airfoils.
Two wing sections with a span of 90 cm and a constant chord of 30 cm were built with the mentioned R-A and R-B airfoils.
In order to examine aspects of the effect of different eddy scales and intensities on the behavior of reflexed airfoils, three different flows were generated in the wind tunnel: a laminar flow and two types of turbulent flows.
One of the turbulent streams was characterized by turbulence with predominant large eddies while the other turbulent flow exhibited rather small eddies. The response of the airfoils submitted to each of these turbulent scale flows transported by the same mean velocity was investigated and compared with its behavior in laminar flow.
The present wind tunnel experiments were conducted at a mean speed of 10 m/sec corresponding to a value of the Reynolds Number of 205000, based on the chord length of the airfoils
The drag and lift measurements were performed on two different constant chord wing sections with reflexed airfoils. Large endplates were placed on the wing tips in order to minimize transversal flows associated to finite span wing effects (Hoerner, 1958; Hoerner, 1975).
The research was accomplished in three steps.
- Design and construction of two wing sections with the two different autostable airfoils mentioned above.
- Generation of two types of turbulence: one with large scale turbulent structures dominance and one with small scale structures prevalence; from now on called 1 and 2 turbulences respectively.
- Measurement of lift and drag for the wing sections submitted to laminar flow and the 1 and 2 turbulences.
A. Experiments
The tests were conducted at the Boundary Layer and Environmental Fluid Dynamics Laboratory (LACLYFA) at the Faculty of Engineering at the Universidad Nacional de La Plata, Argentina.
The wind tunnel described in Boldes et al. (1995) (Fig. 3) is a closed section tunnel with a width of 1.40 m and a height 1 m and a length to height ratio of 7.2 , powered by a 50 HP cc electric motor, equipped with an axial flow variable velocity adjustable pitch blade propeller. The wind speed is continuously variable by means of an electronic speed control between 10 Km/h to 70 Km/h.

Fig. 3 – Wind Tunnel layout for turbulence characterization
At the test section entrance, turbulence was generated with an array of vertical distributed, equally spaced horizontal airfoils, conforming a grid structure. Each airfoil could be individually rotated 360 degrees around its longitudinal axis. For the achievement of the two different turbulences, an adequate distribution of rotation angles of the airfoils was selected, as well as a corresponding floor distribution of roughness elements of two different sizes for each turbulent flow, along the 7.2 meters long working section (Fig. 3). Triangular spikes were placed on the floor at the entrance of the test section (Jackson et al., 1973).
The quality of the flow was judged by comparison with experimental data of field experiments with natural wind.
The reference wind speed U in the wind tunnel was measured at a central point 100-cm upstream from the wing section and 50 cm above the wind tunnel floor with a portable DANTEC Flow Master hot wire anemometer equipped with a 5m long telescopic arm.
This particular mean wind velocity was continuously monitored and kept constant at 10 m/sec during the experiments (Barlow et al., 1999).
The instantaneous velocity measurements of the flow around each wing section (Fig. 4) were carried out using a six channel Dantec Streamline constant temperature hot wire anemometer with X-wire probes (DANTEC, 55R51). For all measurements, 16384 samples for each channel were taken, with a sampling frequency of 600 Hz per channel. The signals were filtered at 300 Hz. to circumvent noise (Bruun, 1973).

Fig. 4 – Mean Velocity Profiles from the Wind Tunnel testing.
Distances, lengths and instantaneous velocities have been made dimensionless in terms of the chord of the airfoils and the reference mean velocity Uh.
The horizontal streamwise direction is the x-axis, the vertical direction is the z-axis and the lateral direction the y-axis.
The instantaneous horizontal, lateral and vertical velocity components were u, v and w respectively.
Lift and drag forces were simultaneously measured by means of a double Wheatstone bridge strain gauge aerodynamic "balance (Tusche, S. 1984; Wiesend, A. 1978)". The data was processed by means of signal conditioners and Vishay serie 2310 amplifiers. The sensitivity of the measure to the balance is about ± 1 gram.
The aerodynamic balance was firmly attached to the surface of the wing section and the tunnel wall.
Both wing sections were tested for angles of attack in an interval of -10o to 20o. In order to adjust air density data, wind tunnel temperature was continuously checked.
The Turbulence Intensity is calculated using the following definition,

where 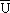 is the mean velocity and u is the fluctuating component of the flow.
is the mean velocity and u is the fluctuating component of the flow.
Turbulence 2 exhibited moderately higher turbulence intensity than turbulence 1, as shown in Fig. 5.

Fig. 5 - Turbulence Intensity Profiles in the Wind Tunnel ( in percentage)
The present paper focuses on single-point velocity statistics describing aspects of the turbulence intensities, extracting turbulent structure characteristics by means of wavelet methodologies.
For the turbulence 1 we selected important energy containing structures at turbulent scales of the order 60 cm corresponding roughly to two times the chord length.
On the other hand for the small scale turbulent flow 2, we found substantial energy containing structures at scales of the order of 40 cm. It is interesting to draw attention to the fact that in the present study the scales of both turbulences were larger than the chord. In future work we will examine the effects of turbulent scales of the order of the boundary layer thickness.
Wavelet analysis allows to determine the time scale and time localization of energetic events (Farge, 1990; 1992), detected as darker spots in the wavelet map. The indication of time scale (ordinate axis in the wavelet map) is multiplied by the mean velocity, using the "frozen flow" model (Hinze, 1975), in order to estimate the turbulent length scales
Figures 6a and 6b show the wavelets maps, of the incident wind on the airfoil taken at the height of 50 cm. Scale data of the main turbulent structures have been extracted from these maps.

Fig. 6a - Wavelets map for Turbulence 1
It is important to emphasize that these curves were obtained at nearly the same mean incident velocity measured at the airfoil height.
The acquired data were corrected for temperature variations, since the density of the air is temperature dependent. The section lift and drag coefficients were corrected for the interference effects of the wind tunnel walls and blockage, using the theory developed by Barlow et al. (1999).

Fig. 6b - Wavelets map for Turbulence 2
After performing the habitual corrections for finite span wings the curves of section lift and drag coefficients against angle of attack were plotted. In addition, the section lift coefficient versus section drag coefficient was drawn (polar curves).
Figure 7 shows the curves of section lift coefficient versus angle of attack, for the two airfoils for laminar flow and the two types of turbulence.
In Fig. 8 the section lift coefficient was plotted versus section drag coefficient for both airfoils the two types of turbulence and the laminar flow. These curves allow us to gain some insight into aspects of the reflexed airfoil behavior

Fig. 7a.- Lift coeficient (Cl) versus incidence angle for R-A airfoil.

Fig. 7b.- Lift coeficient (Cl) versus incidence angle for R-B airfoil.
For airfoil R-A Fig. 7a shows that with laminar flow a slightly better CL/θ behavior is observed for angles of attack as large as 12o. At higher angles of attack the small scale turbulence 2 permits to delay the beginning of stall.
The dissimilar response of the airfoil for the two turbulent scales at angles of attack larger than 10o in the vicinity of the stall region should be noted.
Figure 7b shows that the airfoil R-B also displays the best CL/θ behavior for laminar flow. On the other hand if this airfoil is submitted to turbulence 2 a important lift decrease is observed for nearly all angles of attack up to 15o. It is interesting to observe that turbulence 2 delay stall.
Such lift reduction could have been also achieved in laminar flow by decreasing the airfoil's camber or increasing its reflection.
Figure 8a shows that for the R-A airfoil submitted to the small scale turbulence 2 the CL vs CD curves are shifted toward the higher drag region end therefore impairing the lift to drag ratio, which depreciates the corresponding glide ratio and the aerodynamic efficiency.

Fig. 8a.- Polar curve for the R-A airfoil (Cl vs. Cdd).

Fig. 8b. Polar curve for the R-B airfoil (Cl versus Cdd)
It is noteworthy that for the R-A airfoil operating within the stall region, the best CLversus CD ratio corresponds to large scale turbulence. On the other hand for small scale turbulence a smoother and more controllable stall is observed.
In contrast, the R-B airfoil does not exhibit a clear and differentiated CL/CD response to turbulence as shown in Fig. 8b.
As expected in classical aerodynamic theory the airfoil exposed to laminar flow exhibits a better performance but the stall behavior was always smoothed by both turbulent flows.
Examination of the CL/CD ratio versus angle of attack behavior in Fig. 9a and Fig. 9b shows that before stall, the laminar flow allows always the highest airfoil efficiency. For airfoil R-A large scale turbulence is better than low scale turbulence within the range 0 £ θ £ 13o. For larger angles of attack small-scale turbulence allows a higher efficiency.
Airfoil R-B shows a similar behavior for the flow below or above 9o.

Fig. 9a.- Efficiency versus incidence angle for R-A airfoil.

Fig. 9b. Eficiency versus incidence angle for R-B airfoil.
III. CONCLUSIONS
The experiments describing the interaction of turbulence and two different airfoils showed the existence of a clear influence of turbulent scale and airfoil geometry on wing response.
The present experiments confirm that:
- At angles of attack up to 13o, the laminar flow shows the most efficient lift to drag ratio for both airfoils.
- For turbulent flows airfoil R-A operating at angles of attack up to 13o shows better efficiency for large scale turbulence. Airfoil R-B exhibits also its best efficiency for large scale turbulence but only for angles of attack lower than 8o.
- At very large angles of attack in the stall region the airfoils show a better efficiency for both turbulent flows in comparison to the laminar case. Their best efficiency is achieved for the small-scale turbulence.
- The lift and drag behavior for the different turbulences is clearly connected to airfoil shape.
Standard airfoils are usually designed for steady mean oncoming flows disregarding the nature of the turbulent eddies immersed in the natural wind.
The present experiments suggest the possibility of "tailoring" the shape of an airfoil in order to display its best performance when submitted to turbulence scales of a particular region in which the airplane should operate.
IV. ACKNOWLEDGEMENTS
The authors are gratefully for the support of the Aeronautical Department and the Boundary Layer Wind Tunnel Laboratory at the Engineering Faculty, National University of La Plata, Argentina.
REFERENCES
1. Barlow, J. B., W. H. Rae and A. Pope, "Low-Speed Wind Tunnel Testing", John Wiley & Sons, 3rd edition, 353-361 (1999). [ Links ]
2. Bertin, J. J.; Smith M. L. "Aerodynamics For Engineers", Prentice Hall (1998). [ Links ]
3. Boldes, U., J. Colman and V. Nadal Mora, "The Boundary Layer Wind Tunnel at the Faculty of Engineering, University of La Plata (Argentina)", Latin American Applied Research, 25, 75-85 (1995). [ Links ]
4. Bruun, H. H., "Hot Wire Anemometry. Principles and signal analysis", Oxford university Press Inc., New York (1955). [ Links ]
5. Farge M., "Transformee en ondelettes continue et application a la turbulence", Journ. Annu.Soc. Math., France, 17-62 (1990). [ Links ]
6. Farge M., "Wavelet Transforms and their applications to Turbulence", Annual Rev. Fluid Mechanics, 24, 395-457 (1992). [ Links ]
7. Hinze J. O., "Turbulence", Ed. Mc Graw-Hill (1975). [ Links ]
8. Hoerner S.F., "Fluid - Dynamics Lift", Published by the Author (1975). [ Links ]
9. Hoerner S.F., "Fluid – Dynamics Drag.", Published by the Author (1958). [ Links ]
10. Horten, R. and W. Horten, "Ten Years Development of the Flying Wing High Speed Fighter", Report NoLGB 164, Flying Wing Seminar, Bonn (1943). [ Links ]
11. Jackson, R., J.M.R. Graham and D.J. Maull, "The lift on a wing in a turbulent flow", Aeronautical Quarterly, 24, 155-166 (1973). [ Links ]
12. Liepman, H. W., "Extension of the statistical approach to buffeting and gust response of wings of finite span", Journal of the Aeronautical Sciences, 22, 197-200 (1955). [ Links ]
13. McCormick, B., "Aerodynamics, Aeronautics, and Flight Mechanics", Ed. John Wiley & Sons, (1995). [ Links ]
14. McKeough, P. J. and J.M.R. Graham, "The effect of mean loading on the fluctuating loads induced on aerofoils by a turbulent stream", The Aeronautical Quarterly, 31, 56-69 (1980). [ Links ]
15. Morfey, P.C., "Lift fluctuations associated with unsteady chordwise flow past an airfoil", ASME Journal of Basic Engineering, 92, 663-665 (1970). [ Links ]
16. Ribner, H.S., "Statistical Theory of Buffeting and Gust Response: Unification and Extension", Journal of Aeronautical Sciences, 23, 1075-1118 (1956). [ Links ]
17. Scott, J.R. and H.M. Atassi, "A finite-difference, frequency domain numerical scheme for the solution of the gust response problem", Journal of Computational Physics 119, 75-93 (1995). [ Links ]
18. Sears, W.R. "Some aspects of non-stationary airfoil theory and its practical application", Journal of the Aeronautical Sciences, 18 , 104-108 (1941). [ Links ]
19. Tusche, S. "Interner Bericht: Beschreibung des Konstruktiven Aufbaus und Kalibrierung von 6 - Komponenten - DMS – Windkanalwaagen", DFVLR Interner Bericht 29112-83 A 11 (1984). [ Links ]
20. Wiesnd, A., "Diplomarbeit No 78/1: Experimentelle Bestimmund der LuftKraftbeiwerte von freistehenden Ein - Und Zweifamilienhausern", TU München Diplomarbeit No 78/1 (1978). [ Links ]














