Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.36 n.2 Bahía Blanca abr./jun. 2006
On the use of Lee's protocol for speckle-reduncing techniques
E. Moschetti1, M. G. Palacio1, M. Picco1, O. H. Bustos2 and A. C. Frery3
1 Departamento de Matemática
Facultad de Ciencias Exactas Físico Química y Naturales
Universidad Nacional de Río Cuarto
Ruta 36 km 601, X5804BYA Río Cuarto - Argentina
{emoschetti; gpalacio; mpicco}@exa.unrc.edu.ar
2 Facultad de Matemática, Astronomía y Física
Universidad Nacional de Córdoba
Ing. Medina Allende esq. Haya de la Torre, 5000 Córdoba - Argentina
obustos@arnet.com.ar
3 Instituto de Computação
Universidade Federal de Alagoas 57072-970 Maceió, AL - Brasil
acfrery@pesquisador.cnpq.br
Abstract — This paper presents two new MAP (Maximum a Posteriori) filters for speckle noise reduction and a Monte Carlo procedure for the assessment of their performance. In order to quantitatively evaluate the results obtained using these new filters, with respect to classical ones, a Monte Carlo extension of Lee's protocol is proposed. This extension of the protocol shows that its original version leads to inconsistencies that hamper its use as a general procedure for filter assessment. Some solutions for these inconsistencies are proposed, and a consistent comparison of speckle-reducing filters is provided.
Keywords — Filters. Image Processing. Image Quality. Simulation. Speckle.
I. INTRODUCTION
Contemporary remote sensing relies on data from different regions of the electromagnetic spectrum, the optical, infrared, and microwaves ones. Synthetic Aperture Radar (SAR) sensors are becoming more relevant in every field of research and development that employs remotely sensed data, since they are active and, thus, not requiring external sources of illumination. They can observe the environment in a wavelenght that is little or not affected at all by weather conditions, providing complementary information to the conventional optical sensors.The information these sensors provide is relevant for every remote sensing application, including environmental studies, anthropic activities, oil spill monitoring, disaster assessment, reconnaissance, surveillance and targeting, among others.
As every image obtained using coherent illumination, as is the case of laser, sonar and ultrasound-B imaging, SAR images suffers from speckle noise. Such type of noise do not follows classical Gaussian additive, it is multiplicative noise. Classical techniques for noise reduction are thus inefficient to combat speckle (see, for instance, Allende et al., 2001; Delignon and Pieczynski, 2002; Kuttikkad and Chellappa, 2000; Medeiros et al., 2003; Touzi, 2002).
Since speckle noise hampers the ability to identify objects, many techniques have been proposed to alleviate this issue. Techniques are applied during the generation phase of the images (multilook processing, see Lopes et al., 1990) or after the data is available to the users (processing with filters). A "good' technique must combat speckle and, at the same time, preserve details as well as relevant information.
In order to assess the performance of specklereduction techniques (multilook or filter-based), Lee et al. (1994) proposed a protocol. It consists of a phantom image corrupted by speckle noise processed by speckle-reduction tecniques. Measures of quality are computed on the images obtained, and the performance of the used tecnhique is assessed from these measures. This protocol can be applied to both multilook or filter-based speckle-reduction procedures. In this paper we will discuss the use of this protocol, termed "Lee's protocol', on filter-based techniques.
This papers presents situations where Lee's protocol is inadequate and should be replaced by Monte Carlo experiments; the outline of such simulation is presented. This approach aims at results that are representative for a collection of images, while the ones provided by Lee's protocol regard only one image and, as will be shown, can be biased and uninformative.
Among the many approaches for speckle-reduction using filters, one should mention those based on the noise statistical properties and other general purpose techniques (median, mean etc.). For a comprehensive review of speckle filters the reader is referred to the works by Lee et al. (1994) by Medeiros et al. (2003) and to the references therein.
Among others, Geman and Geman (1984) show the advantage of using stochastic models in image processing. They propose a general transformation setup:
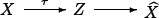
where X represents the unobserved true data, τ transformations imposed by the sensor and Z the observed data. The sensor typically degrades the truth by means of non-linear and non-invertible transformations and with the inclusion of noise. The knowledge of the properties of both X and τ allows building techniques for obtaining 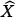 , an estimate of X.
, an estimate of X.
With the above setup and a Bayesian approach, many estimators can be used to compute  as, for instance, maximum likelihood, minimum squared error, maximum posterior mode and maximum a posteriori (MAP). One of the contributions of this paper is the proposal of two new MAP estimators for the ground truth of SAR imagery, and the assessment of their performance.
as, for instance, maximum likelihood, minimum squared error, maximum posterior mode and maximum a posteriori (MAP). One of the contributions of this paper is the proposal of two new MAP estimators for the ground truth of SAR imagery, and the assessment of their performance.
Image quality assessment in general, and filter performance evaluation in particular, are hard tasks (Wang et al., 2002). Many factors are involved as, for instance, the true scene, the degradation and the type of application sought for the data. Lee's protocol is a proposal for filter assessment based on the extraction of measures of quality; in its original version the performance of a filter is assessed using a single image  as input. The use of statistical models allows the proposal of Monte Carlo experiments in order to compute quantities that, as noise reduction performance, depend on many factors and are hard (or impossible) to obtain directly (see, for instance, Bustos and Frery, 1992; Robert and Casella, 2000). We show here that Lee's protocol requires such a Monte Carlo procedure in order to precisely assess the performance of speckle filters.
as input. The use of statistical models allows the proposal of Monte Carlo experiments in order to compute quantities that, as noise reduction performance, depend on many factors and are hard (or impossible) to obtain directly (see, for instance, Bustos and Frery, 1992; Robert and Casella, 2000). We show here that Lee's protocol requires such a Monte Carlo procedure in order to precisely assess the performance of speckle filters.
The paper is organized as follows.Section II presents the multiplicative model. In Section III two new speckle filters based on a Bayesian approach on this model are proposed, after reviewing one of the most widely used techniques: Lee's filter (proposed by Lee, 1986). Section IV presents Lee's protocol, and Section V describes a Monte Carlo experiment used to assess the new filters with respect to the one proposed by Lee et al. (1994); in this section we see that the original protocol is inadequate for filter assessment. Sections VI and VII present the results and conclusions.
II. THE MULTIPLICATIVE MODEL
Only univariate signals will be discussed here; the reader interested in multivariate SAR statistical modelling is referred to Freitas et al. (2005).
Goodman (1985) provided one of the first rigorous statistical frameworks, known as "Multiplicative Model' for dealing with speckle noise in the context of laser imaging. The use of such framework has led to the most successful techniques for SAR data processing and analysis. This phenomenological model states that the observation in every pixel is the out-come of a random variable Z :Ω →  + that, in turn, is the product of two independent random variables: X :Ω →
+ that, in turn, is the product of two independent random variables: X :Ω →  +, the ground truth or backscatter, related to the intrinsic dielectric properties of the target, and Y :Ω →
+, the ground truth or backscatter, related to the intrinsic dielectric properties of the target, and Y :Ω →  +, the speckle noise, obeying a unitary mean Gamma law. The distribution of the return, Z = XY , is completely specified by the distributions X and Y obey. The univariate multiplicative model began as a single distribution, namely the Rayleigh law, was extended by Yueh et al. (1989) to accomodate the K law and later improved further by Frery et al. (1997) to the G distribution, that generalizes all the previous probability distributions.
+, the speckle noise, obeying a unitary mean Gamma law. The distribution of the return, Z = XY , is completely specified by the distributions X and Y obey. The univariate multiplicative model began as a single distribution, namely the Rayleigh law, was extended by Yueh et al. (1989) to accomodate the K law and later improved further by Frery et al. (1997) to the G distribution, that generalizes all the previous probability distributions.
The density function that describes the behavior of the speckle noise is
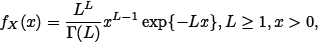 | (1) |
where L is the number of looks, a parameter related to the visual quality of the image and that can be controlled to a certain extent during the generation of the data. An effective filter will tend to increase the value of this parameter, that when is estimated is referred to as "equivalent number of looks".
The most successful models for the backscatter are particular cases of the Generalized Inverse Gaussian distribution (Frery et al., 1997), being the main ones a constant (c) and the Gamma Γ(α, λ), Reciprocal of Gamma Γ-1(α, γ) and Inverse Gaussian IG(ω, σ) laws (for this last see Müller et al., 2000). These models for the backcatter yield the following distributions for the return Z, respectively:
Gamma: characterized by the density function
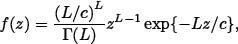 | (2) |
| with c, z > 0 and L ≥ 1, denoted Γ(L, L/c). | |
K: whose density function is
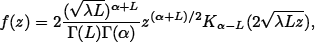
denoted 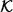 (α, λ, L), where z, α, λ > 0, L ≥ 1, and Kυ is the modified Bessel function of third kind and order υ;
(α, λ, L), where z, α, λ > 0, L ≥ 1, and Kυ is the modified Bessel function of third kind and order υ;
G0: with density function
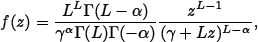 | (3) |
where -α, γ, z > 0, L ≥ 1, denoted  0(α, γ, L). 0(α, γ, L). | |
GH: characterized by the density function
 | (4) |
where ω, σ, z > 0, L ≥ 1, denoted  H(ω, σ, L). H(ω, σ, L). | |
The use of these models in SAR image understanding has led to excellent results, as can be seen in the works by Mejail et al. (2003) and Quartulli and Datcu (2004).
New Bayesian filters for retrieving information on X based on the observation of outcomes of Z will be presented in the next section.
III. SPECKLE FILTERS
One of the most widely used filters for speckle reduction is recalled, namely Lee's filter; then, the general setup for MAP filter is provided and two new Bayesian filters are derived.
A. Lee's filter
This filter (Lee, 1986) aims at combating either multiplicative or additive noise or a combination of both. It uses the observed mean and variance in a window to estimate the (unobserved) true backscatter by
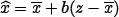
where b is an estimator of the ratio of the variance of X to the variance of Z. If no reliable model for X is available, its moments have to be estimated from the data. The mean and the variance of the backscatter can be estimated in every window by  and by
and by
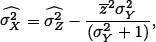
where σY is the speckle standard deviation, that can be easily computed by means of the equivalent number of looks.
B. MAP filters
MAP (maximum a posteriori) filters are a Bayesian approach to the problem of estimating the properties of X given the observation of Z by means of maximizing the posterior distribution of X given Z

Since fZ(z) does not depend on the sought variable x, the MAP estimator is defined as
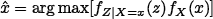
or, since all quantities are positive, as
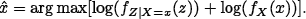 | (5) |
In this work two MAP filters will be derived, those assuming the Γ-1(α, γ) and IG(ω, σ) laws for the backscatter. These filters will be called MAP  0 and
0 and  H. Solving equation (5) in these two situations leads to the following estimators:
H. Solving equation (5) in these two situations leads to the following estimators:
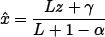 | (6) |
and
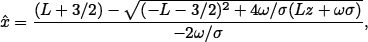 | (7) |
respectively. The equivalent number of looks L is estimated beforehand for the whole image using homogeneous areas (Mejail et al., 2003). The parameters γ, α, ω and σ are estimated locally using the data available in a small window around the position being filtered; among the possible estimation techniques, in this work we used estimators based on the moments of order 1/2 and 1. For maximum likelihood estimation and its numerical issues, the reader is referred to the work by Frery et al. (2004); improved inference by resampling is treated by Cribari-Neto et al. (2002).
The performance of these three filters is assessed in the following sections.
IV. LEE'S PROTOCOL
Lee et al. (1994) proposed a protocol for the performance assessment of speckle reduction techniques. This protocol consists of using a phantom image (see Figure 1(a)) corrupted by speckle noise (see Figure 1(b)) and obtaining measures on the filtered versions; as an example, Figures 1(c) and 1(d) present the results of two candidates for evaluation: Lee's and G0 filters. Since the geometric properties of the uncorrupted phantom are known (points and strips of varying width from 1 to 13 pixels), it is possible to quantitatively assess the behavior of the techniques.

(a) Phantom

(b) Corrupted phantom

(c) Lee filtered data

(d)  0 filtered data
0 filtered data
Figure 1: Lee's Protocol phantom, speckled data and filtered images
The equivalent number of looks, the line contrast and edge preserving are the used criteria to quantify the quality of speckle reduction techniques, determined by
Equivalent number of looks: in intensity imagery and homogeneous areas, it can be estimated by 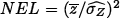 , i.e., the square of the reciprocal of the coefficient of variation.
, i.e., the square of the reciprocal of the coefficient of variation.
Line contrast: since the phantom has a line of one pixel width, the preservation of this line will be
assessed by computing three means: those in the coordinates of the original line (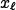 ) and in those corresponding to two lines around it (
) and in those corresponding to two lines around it ( and
and 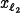 ). The contrast is then defined as 2
). The contrast is then defined as 2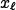 -(
-( +
+ 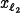 )/2, and compared with the contrast in the phantom image.
)/2, and compared with the contrast in the phantom image.
Edge preserving: it is measured by means of the edge gradient and variance. The former is computed as the absolute difference of the means of strips around edges, while the latter is as the former but using variances instead of means.
The best filter corresponds to the smallest value for all the measures, with exception of the Equivalent number of looks(in this case it occurs the opposit).
It is noteworthy that the original proposal (see Lee et al., 1994) uses a single corrupted image to make the assessment. This is a twofolded limitation, first related to the precision and secondly to the inherent variability of the measures, as we illustrate with an example.
A Monte Carlo version of Lee's protocol is proposed in next section for improved precision and significance, and the filters are then assessed with it.
V. IMPROVED PROTOCOL FOR FILTER ASSEMENT
The result of applying Lee's protocol to an image obtained by simulation is shown in Table 1, where the "best" results are highlighted in boldface. As can be seen, the four criteria lead to conflicting conclusions:
- the best edge gradient is achieved by the
 0 filter but, at the same time, it has the highest variance, which is detrimental;
0 filter but, at the same time, it has the highest variance, which is detrimental; - the equivalent number of looks and the edge variance point at Lee's filter as the best, but it is the worst in line preservation;
- if line preservation were to be used alone, the best filter is
 H.
H.
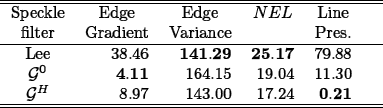
Table 1: Comparison of Speckle filters in a single image
As previously seen, Lee's protocol preconizes the use of quantitative measures for the assessment of specklereduction techniques. Their scale and relative importance are not of the same order, for example the difference in edge variance introduced by Lee's filter and  H is 143.00 - 141.29 = 1.71, while the equivalent number of looks produced by the two MAP filters differ by 19.04 - 17.24 = 1.80, so it remains unclear how, if possible, to combine these results in a single conclusion. Moreover, since no distributional assumption is made on these measures, one does not know anything about the significance of seemingly different results.
H is 143.00 - 141.29 = 1.71, while the equivalent number of looks produced by the two MAP filters differ by 19.04 - 17.24 = 1.80, so it remains unclear how, if possible, to combine these results in a single conclusion. Moreover, since no distributional assumption is made on these measures, one does not know anything about the significance of seemingly different results.
An idea of precision of each measure, and not mere point estimation, becomes thus paramount in order to make fair filter assessments. We propose the use of a Monte Carlo experiment as a means for obtaining this relevant information.
Such simulation experience will also help removing conflicting results as, for instance, the following situation observed for the same set of parameters and two simulated images Z1 and Z2. Using the filtered versions of Z1, one may conclude that Lee's filter is better than  0, since the equivalent number of looks they produce are, respectively, 28.32 and 15.09. But if Z2 filtered images are used, the same measures are 22.54 and 29.88, leading to the opposite conclusion. Same conflicting results arise when other quality measures are applied, so having an idea of the variability of these factors is indispensably necessary.
0, since the equivalent number of looks they produce are, respectively, 28.32 and 15.09. But if Z2 filtered images are used, the same measures are 22.54 and 29.88, leading to the opposite conclusion. Same conflicting results arise when other quality measures are applied, so having an idea of the variability of these factors is indispensably necessary.
Since all the observed data involved have a stochastic nature it is possible to devise Monte Carlo experiments. Such in silico experiment will allow the assessment of the performance of the MAP filters provided by equations (6) and (7), avoiding the risk of basing one's decision on a single observation of a process.
It is necessary to design a Monte Carlo experiment with several situations in order to provide a global assessment of filter performance. This experiment consists of simulating corrupted images as matrices of independent samples of the  0 distribution with different parameters. These parameters are based on previous experience with real data, and depict a few typical situations often encountered when analyzing SAR imagery. These situations stem from a constant background (the original proposal, called "Situation 0") to extremely heterogeneous return (Situations 1 to 6). Besides simulating different types of return, various contrasts between the dark background and the light foreground were also considered. One hundred replications were performed for each of the situations depicted in Table 2.
0 distribution with different parameters. These parameters are based on previous experience with real data, and depict a few typical situations often encountered when analyzing SAR imagery. These situations stem from a constant background (the original proposal, called "Situation 0") to extremely heterogeneous return (Situations 1 to 6). Besides simulating different types of return, various contrasts between the dark background and the light foreground were also considered. One hundred replications were performed for each of the situations depicted in Table 2.
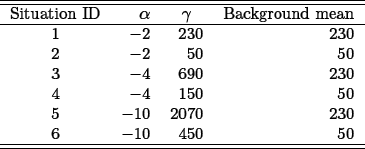
Table 2: Simulated situations with the 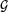 0(α, γ) distribution
0(α, γ) distribution
Every simulated image was subjected to Lee's and MAP  0 and
0 and  H filters with windows of size 7 × 7, and the comparison was perfomed by means of the criteria presented in Section IV.
H filters with windows of size 7 × 7, and the comparison was perfomed by means of the criteria presented in Section IV.
VI. RESULTS
The results obtained are summarized by means of boxplots. Each boxplot describes the results of one filter in a particular situation, using one hundred replications.
Figure 2 shows the boxplots of the four metrics corresponding to three filters in seven situations. Vertical axes are coded by means of the filter ('L' for Lee, 'G' for  0 and 'H' for
0 and 'H' for  H ) and the situation (from 0 to 6). All results exhibit a notorious variability with an exception: when both background and foreground truth are constant, i.e., when there is no backscatter variation. Besides this variability, little can be said in order choose amongst the filters in the situations considered with the metrics proposed.
H ) and the situation (from 0 to 6). All results exhibit a notorious variability with an exception: when both background and foreground truth are constant, i.e., when there is no backscatter variation. Besides this variability, little can be said in order choose amongst the filters in the situations considered with the metrics proposed.
In the original situation (#0), for instance, though there is little variability the values are almost the same for the four metrics. In situation #1 only edge variance is capable of making a discrimination, and Lee is the best filter (see Figure 2(d)). For situation #2, the Lee filter is the best one with respect to all criteria with the exception of edge variance; for this last criterion there is no difference among filters. In situation #3 only edge variance is capable of discrimination, pointing at Lee as the best filter. Regarding situation #4, Lee filter is the best with respect to line preservation, but the worst regarding edge variance. In situation #5 both MAP filters show improvement with respect to Lee in both edge gradient and edge variance. Finally, when situation #6 is considered, though there is no clear evidence, Lee is better than the other two in all criteria but one: edge variance.
One can conclude, then, that the original Lee's protocol is inadequate for filter comparison when realistic situations are considered, e.g, when either background or foreground or both vary. More sensitive mea-sures should be used to solve this limitation.Sant'Anna (1995) proposes a means to mix different metrics in a single scalar allowing, thus, to assessing filters with a grade. Wang and Bovik (2002) also propose a scalar metric for image quality assessment.
VII. CONCLUSIONS
This paper presented two new MAP filters for speckle noise reduction and a Monte Carlo experiment that improves the original proposal. When trying to assess their perfomance using this simulation setup, we noticed that this procedure is inadequate to deal with situations more realistic than constant background.
Previous works (see, for instance, Medeiros et al., 2003; Sant'Anna, 1995) relate the superior behavior of MAP filters with respect to Lee's filter, but the high variability of the measures proposed by Lee's protocol hampers a straightforward comparison.
Other measures are showing a good potential for this assessment, such as the image index quality provided by Oliver and Quegan (1998) and the edge preserving index proposed by Sattar et al. (1997).
Monte Carlo experiments must be devised within the framework of statistical modelling in order to make sensible comparisons among filters.
REFERENCES
1. Allende, H., J. Galbiati and R. Vallejos, "Robust image modelling on image processing", Pattern Recognition Letters, 22, 1219-1231 (2001). [ Links ]
2. Bustos, O.H. and A.C. Frery, Simulação estocástica: teoria e algoritmos (versão completa), Monografias de Matemática, 49, CNPq/IMPA, Rio de Janeiro (1992). [ Links ]
3. Cribari-Neto, F., A.C. Frery and M.F. Silva, "Improved estimation of clutter properties in speckled imagery", Computational Statistics and Data Analysis, 40, 801-824 (2002). [ Links ]
4. Delignon, Y. and W. Pieczynski, "Modeling non-Rayleigh speckle distribution in SAR images", IEEE Transactions on Geoscience and Remote Sensing, 40, 1430-1435 (2002). [ Links ]
5. Freitas, C.C., A.C. Frery and A.H. Correia, "The polarimetric G distribution for SAR data analysis", Environmetrics, 16, 13-31 (2005). [ Links ]
6. Frery, A.C., F. Cribari-Neto and M.O. Souza, "Analysis of minute features in speckled imagery with maximum likelihood estimation", EURASIP Journal on Applied Signal Processing, 2004, 2476-2491 (2004). *http://www.hindawi.com/GetArticle.aspx?pii=S111086570440907X [ Links ]
7. Frery, A.C., H.-J. Müller, C.C.F. Yanasse and S.J.S. Sant'Anna, "A model for extremely heterogeneous clutter", IEEE Transactions on Geoscience and Remote Sensing, 35, 648-659 (1997). [ Links ]
8. Geman, D. and S. Geman, "Stochastic relaxation, Gibbs distributions and the Bayesian restoration of images", IEEE Transactions on Pattern Analysis and Machine Intelligence, 6, 721-741 (1984). [ Links ]
9. Goodman, J.W., Statistical Optics, Wiley, New York (1985). [ Links ]
10. Kuttikkad, S. and R. Chellappa, "Statistical modelling and analysis of high-resolution synthetic aperture radar images", Statistics and Computing, 10, 133-145 (2000). [ Links ]
11. Lee, J.S., "Speckle suppression and analysis for synthetic aperture radar images", Optical Engineering, 25, 636-643 (1986). [ Links ]
12. Lee, J.S., I. Jurkevich, P. Dewaele, P. Wambacq and A. Oosterlink, "Speckle filtering of synthetic aperture radar images: a review", Remote Sensing Reviews, 8, 313-340 (1994). [ Links ]
13. Lopes, A., H. Laur and E. Nezry, "Statistical distribution and texture in multilook and complex SAR images", International Geoscience and Remote Sensing Symposium, New York, 2427-2430 (1990). [ Links ]
14. Medeiros, F.N.S., N.D.A. Mascarenhas and L.F.Costa, "Evaluation of speckle noise MAP filtering algorithms applied to SAR images", International Journal of Remote Sensing, 24, 5197-5218 (2003). [ Links ]
15. Mejail, M.E., J. Jacobo-Berlles, A.C. Frery and O.H. Bustos, "Classification of SAR images using a general and tractable multiplicative model", International Journal of Remote Sensing, 24, 3565-3582 (2003). [ Links ]
16. Müller, H.-J., A.C. Frery, J. Jacobo-Berlles, M.E. Mejail and J. Moreira, "The Harmonic branch of the multiplicative model: properties and applications", Third European Conference on Synthetic Aperture Radar (EUSAR), München, 603-606 (2000). [ Links ]
17. Oliver, C. and S. Quegan, Understanding Synthetic Aperture Radar Images, Artech House, Boston (1998). [ Links ]
18. Quartulli, M. and M. Datcu, "Stochastic geometrical modeling for built-up area understanding from a single SAR intensity image with meter resolution", IEEE Transactions on Geoscience and Remote Sensing, 42, 1996-2003 (2004). [ Links ]
19. Robert, C.P. and G. Casella, Monte Carlo Statistical Methods, Springer, New York (2000). [ Links ]
20. Sant'Anna, S.J.S., Avaliação do desempenho de filtros redutores de speckle em imagens de radar de abertura sintética, Dissertação de Mestrado em Sensoriamento Remoto, Instituto Nacional de Pesquisas Espaciais, São José dos Campos, Brasil (1995). [ Links ]
21. Sattar, F., L. Floreby, G. Salomonsson and B. Lövström, B., "Image enhancement based on a nonlinear multiscale method", IEEE Transction on Image Processing, 6, 888-895 (1997). [ Links ]
22. Touzi, R., "A review of SAR image speckle filtering", IEEE Transactions on Geoscience and Remote Sensing, 40, 2392-2404 (2002). [ Links ]
23. Wang, Z. and A.C. Bovik, "A universal image quality index", IEEE Signal Processing Letters, 9, 81-84 (2002). [ Links ]
24. Wang, Z., A.C. Bovik and L. Lu,"Why is image quality assessment so difficult?", IEEE International Conference on Acoustics, Speech & Signal Processing Proceedings, 4, 3313-3316 (2002). [ Links ]
25. Yueh, S.H., J.A. Kong, J.K. Jao, R.T. Shin and L.M. Novak , "K-distribution and polarimetric terrain radar clutter", Journal of Electromagnetic Waves and Applications, 3, 747-768 (1989). [ Links ]
Received: September 21, 2005.
Accepted for publication: February 6, 2006.
Recommended by Guest Editors C. De Angelo, J. Figueroa, G. García and J. Solsona.














