Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.36 n.3 Bahía Blanca jul./sept. 2006
Modeling of Fischer-Tropsch synthesis in a tubular reactor
L. C. A. Mazzone and F. A. N. Fernandes
Universidade Federal do Ceará, Departamento de Engenharia Química,
Campus do Pici, Bloco 709, 60455-760 Fortaleza - CE, Brazil
fabiano@efftech.eng.br
Abstract — Fischer-Tropsch synthesis is an important chemical process for the production of liquid fuels and olefins. In recent years, the abundant availability of natural gas and the increasing demand of olefins and liquid fuels have led to a high interest to further develop this process. A mathematical model of a tubular reactor used for syngas polymerization was developed and the carbon monoxide polymerization was studied from a modeling point of view. Simulation results show that different parameters affect syngas conversion and carbon product distribution, such as operating pressure, gas velocity and syngas composition. Optimization of several hydrocarbon products were done in order to search for the best operating conditions for their production.
Keywords — Multitubular Reactor. Fischer-Tropsch Synthesis. Liquid Fuels. Olefins.
I. INTRODUCTION
In recent years, the Fischer-Tropsch Synthesis (FTS) became a subject of renewed interest particularly in the context of the conversion of remote natural gas into liquid transportation fuels and due to an escalation in the price of oil. Natural gas, biomass and coal can be converted to carbon monoxide and hydrogen (synthesis gas) via the existing processes, such as steam reforming, carbon dioxide reforming, partial oxidation and catalytic partial oxidation. The syngas can be converted into hydrocarbons (paraffins and olefins) by the FT synthesis reaction:
 | (1) |
The FT synthesis can be carried out in iron, cobalt and ruthenium based catalysts. Fe-based catalysts are much less expensive than the Co-based catalysts, which can be an important economical factor for the process specially because the catalyst has to be replaced due to deactivation. When iron catalysts are used, the carbon monoxide polymerization occurs in combination with the water gas shift reaction (WGS):
CO + H2O ↔ CO2 + H2. (2)
Many researchers have been working on catalyst development (Raje and Davis, 1997; van Steen and Schulz, 1999) and reactor design (Maretto and Krishna, 1999; Krishna and Sie, 2000; Krishna et al., 2001; Wang et al., 2003), but few investigations have been done in order to optimize the production of specific products.
The Fischer-Tropsch reaction yields predominately straight chain hydrocarbons (α-olefins and alkanes) where the main reaction products are α-olefins. There is general agreement that the reaction may be viewed as a methylene polymerization reaction where the monomer unit (=CH2), is not initially present. The products are formed by hydrogenation of CO to generate the methylene monomer, in situ. Polymerization occurs through initiation of chains, competing chain propagation and chain termination steps. Theories on the CO polymerization mechanism are based in the superposition of two ASF (Anderson-Schulz-Flory) distributions and rely in the dual site theory (Madon and Taylor, 1981), secondary chain growth of read-sorbed alkenes theory (Schulz and Claeys, 1990; Iglesia et al., 1991), or the dual mechanism of chain growth theory (Patzlaff et al., 1999, 2002). Iron catalysts are more likely to obey a dual mechanism of chain growth theory.
In this work a mathematical model of a tubular reactor used for CO polymerization was developed and the carbon monoxide polymerization was studied from a modeling point of view based on the kinetics of an iron catalyst obeying a dual mechanism theory.
II. TUBULAR REACTOR
The tubular reactor for Fischer-Tropsch synthesis consists of a multitube reactor where the synthesis gas is fed at the top of the reactor and passes through the bed of catalyst inside the tubes. The synthesis gas passes through the reactor in plug-flow regime. Water passes through the shell side of the multitube reactor to remove the heat released by the FTS reaction and to control the reactor temperature, ensuring an isothermal condition inside the reactor, in spite of the high heat of reaction (ΔH = - 170 kJ/mol CO).
III. MATHEMATICAL MODEL
A. Tubular Reactor Model
The basic assumptions made for the reactor were: steady-state operation, isothermal conditions, gas passing through the reactor in plug-flow regime due to its velocity, hydrocarbon products in the gas and in the liquid phases are assumed to be in equilibrium at the reactor outlet; mass and heat transfer resistances between the catalyst and the gas phase is negligible; negligible radial concentration and temperature gradient within the tube; negligible concentration and temperature gradient within the catalyst; intrinsic kinetics for Fischer-Tropsch synthesis and water-gas shift reactions.
The kinetic model for the FTS reaction on an iron catalyst and for the WGS reaction are given by (Raje and Davis, 1997):
 | (3) |
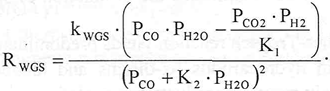 | (4) |
The material balance for component i in the reactor as a function of its axial position is given by:
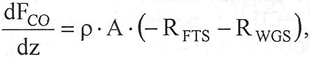 | (5) |
 | (6) |
 | (7) |
 | (8) |
The partial pressure of the species is given by:
 | (9) |
Due to the assumption of isothermal condition in the reactor, which can be considered based on the academic and patent reports (Freide et al., 2003, 2004; Wang et al., 2003), only the mass balances and population balances for the hydrocarbon species were considered in this work. As such, all heat produced by the reaction is assumed to be removed by the cooling jacket of the reactor.
The momentum equation was modeled considering the flow through a packed bed, following the Ergun equation:
 | (10) |
To solve the mathematical model, the model equations were numerically integrated using a 5th order Runge-Kutta method. The kinetic parameters for the reaction are presented in Table 1, the operating conditions used in the simulations are presented in Table 2. The overall kinetic rates for the Fischer-Tropsch reaction and the WGS reaction were taken from Raje and Davis (1997). The physical properties of the gases were calculated according to Peng-Robinson equation of state.
Table 1. Kinetic parameters for Fischer-Tropsch synthesis in iron catalyst and for water gas shift (Raje and Davis, 1997).

* Obtained experimentally at T = 270oC, P = 0.5 - 3.0 MPa and H2/CO = 0.67 - 1.7.
Table 2. Operating conditions and reactor parameters.

B. Kinetic model
The kinetic model used to simulate the CO polymerization and product distribution assumes that the alkyl and alkenyl mechanism acts together in the FTS synthesis.
The alkyl mechanism can be represented by the following reactions:
 | initiation |
 | propagation |
 | reduction by surface hydride giving alkanes |
 | β-hydride elimination giving a olefins |
The alkenyl mechanism can be represented by the following reactions:
 | initiation |
 | propagation |
 | reduction giving olefins |
Methane and ethane are formed by the following reactions:
 | reduction by surface hydride giving methane |
 | methylene termination |
The mass balance for the FTS is given by the following set of equations (Fernandes, 2005):
 | (11) |
 | (12) |
 | (13) |
 | (14) |
 | (15) |
 | (16) |
 | (17) |
 | (18) |
 | (19) |
The development of the mass balances assumes that the quasi-steady state is applied to the concentration of the propagating species (as assumed for the zero order moment of live polymers); the consumption of methylene units is proportional to the global reaction rate; and the concentration of hydrogen in the polymerization site is proportional to the partial pressure of hydrogen in the reaction media. The kinetic parameters for the CO polymerization are presented in Table 3.
Table 3. Kinetic parameters for CO polymerization in iron catalyst (at 270oC).

The model has been validated using the data reported by Raje and Davis (1997) and Donnelly and Satterfield (1989). Variance analysis was done using the software Statistica 5.0 which showed that the model is significant within 99% of confidence (Fernandes, 2005).
IV. RESULTS AND DISCUSSION
Fischer-Tropsch synthesis in tubular reactors is a complex system with many process variables that should be accounted for: gas velocity, catalyst density, total pressure, H2:CO ratio. Studies on how gas velocity and pressure affects conversion and total production of hydrocarbons have been made by several authors (Maretto and Krishna, 1999; Krishna and Sie, 2000; Krishna et al., 2001; Wang et al., 2003), but few studies have been made on how these parameters affect the product distribution.
In this work, several simulations were made to understand the effect of pressure, gas velocity and hydrogen to carbon monoxide ratio on the product distribution, especially in the range of transportation fuels and olefins. The simulation study assumes that the rate laws for the FT and WGS kinetics are valid for the entire range of the varied process parameters. Some extrapolations were done but kept near the experimental regime of Raje and Davis (1997), and Donnelly and Satterfield (1989). The extrapolation on pressure was more significant, but in a related work Davis (2003) has stated that for this catalyst the effect of pressure (from 0.5 to 3 MPa) over trie overall kinetic rate is not significant. This information is also supported by Dry (1996) and by Li et al. (2002). On the other hand, temperature has a great effect on the kinetic rate laws and as we do not have information on the effects of temperature over the kinetic rates, the temperature was not subjected to variations in this study and as such the system behavior was considered at 270oC.
In general, conversion of syngas increases with H2:CO ratio. As the H2:CO ratio approaches 2.0 the amount of syngas converted to hydrocarbons (FTS) and water (WGS) increases. As conversion increases, the WGS reaction increases its rate due to the production of more water by the FTS reaction, and although CO conversion may be at 92% (40 arm, UG = 1.0 m/s, H2:CO=2.0), the hydrocarbon yield is at 88% (Fig. 1).

Figure 1. CO conversion as function of H2:CO ratio for two different gas velocities (conditions: 40 atm, 270oC). Full lines represent total syngas conversion. Dashed lines represent hydrocarbon yield.
Hydrogen is responsible for the termination of hydrocarbon chains into paraffins. As such an increase in the H2:CO feed ratio will increase the partial pressure of H2 in the reaction media and thus increase the termination rate into paraffins, reducing the amount of olefins produced by the reaction (Fig. 2). At low H2:CO ratios, the fraction of olefins production is at its maximum since the amount of hydrogen is small enough not to produce great quantities of paraffins. As the H2:CO ratio increases the termination into paraffin increases and the ratio of olefin to paraffin tends to zero.

Figure 2. CO yield into olefins as function of H2:CO ratio (conditions: 20 atm, 270oC, UG = 1.0 m/s). Full line represent total olefin yield. Dashed lines represent CO yield into O2-4 and O5+.
As the H2:CO ratio increases the production of light olefins increases steeply, since chain termination occurs preferably towards paraffins, leading to the production of a greater quantity of light olefms and light paraffins (Fig. 3). An increase in the gas velocity enhances the production of olefins since the higher gas velocity increases the concentration of the reagents as an effect of the residence time in the reactor. The increase in the carbon monoxide partial pressure is higher than the increase in the hydrogen partial pressure, and as such the propagation rate increases more than the termination rate (influenced by the hydrogen partial pressure) leading to an increase in the average hydrocarbon chain length (Figs. 3, 4).

Figure 3. Light olefms yield (CM) as function of H2:CO ratio and gas velocity (conditions: 270oC, 40 atm).

Figure 4. C5+ olefins yield as function of H2:CO ratio and gas velocity (conditions: 270oC, 40 atm).
The total pressure did not show any major influence on CO conversion and hydrocarbon yield. An increase in the total pressure in the system reduces CO conversion and increases the hydrocarbon yield (about 2 to 15% for each 10 atm increase). This happens because the rate of the FT reaction is directly proportional to the total pressure; the rate of the WGS is not directly affected by the total pressure, but coupled to the H2O partial pressure, which depends on the conversion level. The H2O partial pressure also inhibits the FT reaction and its increase causes the conversion to decrease. On the other hand, the productivity (ton/h) is favored by the increase in total pressure since the reaction rate is proportional to the total pressure.The effect on productivity however is significant and an 10 atm increase in pressure increases the productivity in approximately 50% due to the higher concentration of CO and H2 in the reactor (Fig. 5).

Figure 5. Reactor productivity as function of pressure and gas velocity (conditions: 270oC, H2:CO = 2.0).
Lower pressures favor the WGS reaction and the FTS reaction will be responsible only for 79% of the CO consumption (at UG = 1.0 m/s, H2:CO = 0.5; PT = 20 atm), while higher pressures favors the FTS reaction and CO consumption by this reaction is as high as 98% (at UG = 10.0 m/s, H2:CO = 0.5; PT = 40 atm). The yield of light olefins changes only slightly with gas velocity but is strongly influenced by pressure where an enhancement of up to 100% can be achieved by changing the operating pressure from 20 to 40 atm (UG = 1.0 m/s; H2:CO = 2.0) (Fig. 6). The yield of C5+ olefins is influenced both by gas velocity and total pressure, where the maximum yield of C5+ olefins is at high gas velocities and high operating pressures (UG = 10.0 m/s; PT= 40 atm) (Fig. 7). Gasoline production is favored by high pressures and high gas velocities and a maximum of 4.8% of gasoline (weight percentage) is produced in the reaction. The highest amount of diesel obtained was 1.9% weight percentage, which is unsuitable for industrial applications.

Figure 6. Light olefins production (in weight fraction) as function of pressure and gas velocity (conditions: 270oC, H2:CO = 2.0).

Figure 7. Heavy olefins (C5+) production (in weight fraction) as function of pressure and gas velocity (conditions: 270oC, H2:CO = 1.0).
These results show that the total pressure of the system and the hydrogen to carbon monoxide ratio are the major factors to be set depending on the most desirable product to be produced. As a rule of thumb, the higher the pressure, the higher the chain length of the hydrocarbon that is produced by the reaction.
A. Product Optimization
Optimization of the FT synthesis was conducted searching for the operating conditions that result in the highest production of gasoline, light olefins and higher olefins. A program in Fortran was developed in order to maximize the production of these products, using the method of quasi-Newton and a finite-difference gradient. The search for the optimum operating conditions is time consuming and the system presents some local maxima that need to be avoided, so several initial values for the maximization where used and the best values are shown on Tables 4 to 7.
Hydrocarbon yield (mass basis) and productivity of each product have different maximum points and so, the optimization function can focus in one of these two factors. The focus presented herein is on the maximum productivity (kg/h per tube) and on the maximum yield (maximum mass fraction) of gasoline, light olefins and higher olefins, which are the main target products for this iron catalyst. Table 4 presents a summary of the optimal operating conditions for maximum yields of gasoline, light olefins and higher olefins; and Table 5 presents the product distribution for the optimum conditions for the following optimization problem:

Table 4. Optimal operating conditions for maximum yields of gasoline, light olefins and higher olefins.

Table 5. Product distribution (weight fraction) of reactor operating at the optimum conditions for maximum yields of gasoline, light olefins and higher olefins.
Higher concentrations of reacting gases in the reaction media (high pressure and gas velocity) associated with low hydrogen to carbon monoxide ratio is the best operating conditions to maximize the yield of gasoline in the FTS reaction. Higher concentration of reacting gases in the reaction media (high pressure and gas velocity) are also the best operating conditions to maximize the yield of higher olefins, but in this case the hydrogen to carbon monoxide ratio has to be greater than 1.45. For the optimization of light gases the reactor pressure should be at 1.0 MPa, which benefits the termination of hydrocarbon chains, leading to short chains.
Some operating conditions shown in Table 4 are at the upper or lower limits of the constraints imposed in the optimization procedure. A broader optimization limits could be done but this would lead to results far away from which the kinetic rate constants were validated for and it would not be possible to ensure the reliability of the results.
Table 6 presents a summary of the optimal operating conditions for maximum production of gasoline, light olefins and higher olefins; and Table 7 presents the production distribution for the optimum conditions for the following optimization problem:

Table 6. Optimal operating conditions for maximum production of gasoline, light olefms and higher olefins.

Table 7. Product distribution (weight basis) of reactor operating at the optimum conditions for maximum production of gasoline, light olefins and higher olefins (kg/h per tube).
When the maximization focuses on the mass production of the desired product the operating conditions are different from the conditions for maximum yields. Pressure and gas velocity are maintained since maximum production is also associated to higher gas concentrations. The H2:CO ratios for maximum production are higher than for maximum yield, existing a trade-off from reducing the average chain length towards a higher mass production associated to higher propagation rates.
As shown in Table 7, when light olefins are the desired product, the production of heavy olefins (C5+) is at 7.4 kg/h per tube, but when the H2:CO ratio is increased, the average chain length of paraffins diminishes and the average chain length of olefins increases, producing 9.0 kg/h per tube of heavy olefins. As H2:CO ratio is increased, the production of light paraffins increases, producing a greater quantity of methane and ethane which has to be recycled back to the reformer to produce syngas.
Decision on which optimum point to choose: maximum production or maximum yield may depend on economical reasons. Running the system with the operating conditions that favors maximum yield will lead to lower costs on recycling and burning of unwanted products (paraffin light gases and LPG) but production will be lower for the same reactor size. While running the system with the operating conditions which favor maximum production will lead to higher recycling costs which may be compensated by the enhanced production rate.
V. CONCLUSIONS
Fischer-Tropsch synthesis can be used to produce transportation fuels and olefins from natural gas and the polymerization conditions can be set to maximize the production of a certain product generated by the FTS reaction, such as light olefms, higher olefins and gasoline.
According to the simulations, the optimum operating condition to maximize heavy olefins production and yield needs high pressures and high gas velocity associated to hydrogen to carbon monoxide ratios between 1.45 and 1.75. The optimum operating condition to maximize light olefms production needs high pressures and high gas velocity associated to hydrogen to carbon monoxide ratios between 0.50 and 0.90. The production of gasoline and diesel using this iron-based catalyst is not economically viable in this kind of reactor since their yields are lower than 5% in mass weight while some commercial catalyst presents yields higher than 15% in mass weight.
NOMENCLATURE
| A | area [m2] |
| Ci,j | concentration of component i |
| Fi | molar flow rate of component i [mol.h-1] |
| dp | catalyst particle diameter [m] |
| H | reactor height [m] |
| ket | ethane formation rate constant [MPa-1.h-1] |
| ki | initiation rate constant for the alkyl mechanism [MPa-1] |
| ki2 | initiation rate constant for the alkenyl mechanism [mol/h] |
| kmet | methane formation rate constant [MPa-1.h-1] |
| kO2 | ethylene formation rate constant [h/mol] |
| kolef | termination by b-elimination rate constant for the alkyl mechanism [h-1] |
| kolef2 | termination rate constant for the alkenyl mechanism [h-1] |
| kp | propagation rate constant for the alkylmechanism [h/mol] |
| kp2 | propagation rate constant for the alkenyl mechanism [h/mol] |
| kpar | termination rate constant for the alkyl mechanism yielding paraffin [MPa-1.h-1] |
| Ki | equilibrium constant of reaction i or adsorption coefficient of component i |
| Pi | partial pressure [MPa] |
| PT | total pressure in the reaction zone [MPa] |
| P(n) | paraffin containing n carbons [mol] |
| P=(n) | olefin containing n carbons [mol] |
| Ri | rate of reaction / [mol/s.kgcat] |
| R(n) | alkyl propagating species containing n carbons [mol] |
| R"(n) | alkenyl propagating species containing n carbons [mol] |
| RFTS | overall Fischer-Tropsch reaction rate |
| T | temperature [K] |
| UG | gas velocity [m/s] |
| wi | weight fraction of hydrocarbon with i carbons in the product distribution |
| XCO | carbon monoxide conversion |
| Y | hydrocarbon yield |
| z | axial position [m] |
 | porosity |
| ν | stoichiometric coefficient |
| μ | gas mixture viscosity [N.s/m2] |
| ρ | catalyst density [kg/m3] |
| ρg | gas mixture density [kg/m3] |
ACKNOWLEDGMENT
The authors gratefully acknowledge the financial support of the Brazilian research funding institution CNPq/CTPetro (Conselho Nacional de Desenvolvimento Científico).
REFERENCES
1. Davis, B.H., "Fischer-Tropsch Synthesis: Relationship between Iron Catalyst Composition and Process Variables." Cat. Today, 84, 83-98 (2003). [ Links ]
2. Donnelly, T.J. and C.N. Satterfield, "Product distributions of the Fischer-Tropsch synthesis on precipitated iron catalysts." Appl. Catal., 52, 93-114 (1989). [ Links ]
3. Dry, M.E., "Practical and theoretical aspects of the catalytic Fischer-Tropsch process." Appl. Catal., 138, 319-344 (1996). [ Links ]
4. Fernandes, F.A.N., "Polymerization Kinetics of Fischer-Tropsch Reaction on Iron Based Catalysts and Product Grade Optimization". Chem. Eng. Tech., 28, 930-938 (2005). [ Links ]
5. Freide, J.J.H.M.F., T.D. Gamlin, C. Graham, J.R. Hensman, B. Nay and C. Sharp, "An adventure in catalysis: the story of the BP Fischer-Tropsch catalyst from laboratory to full-scale demonstration in Alaska", Topics Catal., 26, 3-12 (2003). [ Links ]
6. Friede, J.J.H.M.F., J.R. Hensman, N. David, C. Sharp, G.B. Smith. "Fischer-Tropsch Process". European Patent EP1392622 (2004). [ Links ]
7. Iglesia, E., S.C. Reyes and R.J. Madon, "Transport-enhanced α-olefin readsorption pathways in Ru-catalyzed hydrocarbon synthesis." J. Catal., 129, 238-256 (1991). [ Links ]
8. Krishna, R. and S.T. Sie, "Design and Scale Up of the Fischer-Tropsch Bubble Column Slurry Reactor." Fuel Proc. Tech., 64, 73-105 (2000). [ Links ]
9. Krishna, R., J.M. van Baten, M.I. Urseanu, and J. Ellenberger, "Design and Scale Up of a Bubble Column Slurry Reactor for Fischer-Tropsch Synthesis." Chem. Eng. Sci., 56, 537-545 (2001). [ Links ]
10. Li, S., S. Krishnamoorthy, A. Li, G.D. Meitzner and E. Iglesia, "Promoted Iron-Based Catalysts for the Fischer-Tropsch Synthesis: Design, Synthesis, Site Densities, and Catalytic Properties." J. Catal., 206, 202-217 (2002). [ Links ]
11. Madon, R.J. and W.F. Taylor, "Fischer-Tropsch synthesis on a precipitated iron catalyst." J. Catal., 69, 32-43 (1981). [ Links ]
12. Maretto, C. and R. Krishna, "Modelling of a Bubble Column Slurry Reactor for Fischer-Tropsch Synthesis." Cat. Today, 52, 279-289 (1999). [ Links ]
13. Patzlaff, J., Y. Liu, C. Graffmann and J. Gaube, "Studies on product distributions of iron and cobalt catalyzed Fischer-Tropsch synthesis." Appl. Catal., 186, 109-119 (1999). [ Links ]
14. Patzlaff, J., Y. Liu, C. Graffinann, and J. Gaube, "Interpretation and Kinetic Modeling of Product Distributions of Cobalt Catalyzed Fischer-Tropsch Synthesis." Cat. Today, 71, 381-394 (2002). [ Links ]
15. Raje, A.P. and B.H. Davis, "Fischer-Tropsch Synthesis over Iron-Based Catalysts in a Slurry Reactor. Reaction Rates, Selectivities and Implications for Improving Hydrocarbon Productivity." Cat.Today, 36, 335-345 (1997). [ Links ]
16. Schulz, H. and M. Claeys, "Kinetic Modelling of Fischer-Tropsch Product Distributions." Appl. Catal., 186, 91-107 (1990). [ Links ]
17. van Steen, E. and H. Schulz, "Polymerization Kinetics of the Fischer-Tropsch CO Hydrogenation using Iron and Cobalt Based Catalysts." Appl. Catal., 186, 309-320 (1999). [ Links ]
18. Wang, Y.N., Y.Y. Xu, Y.W. Li, Y.L. Zhao and B.J. Zhang, "Heterogeneous Modeling for Fixed Bed Fischer-Tropsch Synthesis: Reactor Model and its Applications." Chem. Eng. Sci., 58, 867-875 (2003). [ Links ]
Received: September 28, 2005.
Accepted: December 27, 2005.
Recommended by Subject Editor G. Meira.














