Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.36 n.4 Bahía Blanca oct./dic. 2006
Modeling an simulation of an autothermal reformer
J. Piña and D. O. Borio
PLAPIQUI (UNS-CONICET), Camino La Carrindanga Km 7. (8000) Bahía Blanca, Argentina.
julianap@plapiqui.edu.ar
Abstract — The steady-state operation of the autothermal reformer is simulated as two reactors in series by means of a detailed mathematical model. An input-output model is selected to describe the upper combustion chamber. The possible occurrence of homogeneous steam reforming and water-gas-shift (WGS) reactions is considered. The catalyst bed is represented through a one-dimensional heterogeneous model, which allows calculating the axial variations of composition, temperature and pressure of the process gas stream. The strong intraparticle diffusional limitations are taken into account by rigorous solution of the mass balances inside the catalyst particle. The gas-solid heat-transfer resistances are also evaluated. An intrinsic kinetics is used for the steam reforming and WGS reactions. Heat losses to the environment are considered. The influence of the main operating variables on the reactor performance is studied. The proposed mathematical has been checked successfully against data available in the open literature.
Keywords — Autothermal Reforming. Synthesis Gas. Reactor Modeling.
I. INTRODUCTION
Synthesis gas is a major route from hydrocarbons to many important chemicals made up from H2 and CO. The interest in conversion of natural gas (NG) to liquid fuels (GTL) has grown significantly over the last decades (Christensen et al., 1998). GTL processes require different ratios between H2 and CO depending on the specific synthesis. For all the products, the synthesis gas section is the most capital and energy intensive part of the plant (Dybkjaer and Christensen, 2001). The traditional technology for syngas production is steam reforming. The main drawbacks of this technology for GTL applications are the significant energy requirement (due to the strong endothermicity of the reforming reactions) and the high initial investments (the steam reforming section is responsible for 50-75% of the capital costs; Dybkjaer and Christensen, 2001).
Autothermal reforming (ATR), one of the alternatives to steam reforming of methane, has received considerable attention for several advantages, including its relative compactness, lower capital cost, greater potential for economies of scale and its flexibility with respect to the product composition (Christensen and Primdahl, 1994). The ATR consists of a single reactor system, in which hydrocarbons are completely converted into a mixture of H2 and CO. The process is "autothermal" in that the partial combustion of a portion of the hydrocarbon feed provides the heat required by the endothermic reforming reactions to proceed. The ATR unit, illustrated in Fig. 1, is a refractory-lined pressure vessel containing a burner, a combustion chamber and a catalyst bed. The hydrocarbon feedstock is mixed with steam and pure oxygen, enriched-air or air in a specially designed burner located at the top of the reactor. In the combustion chamber (upper part), the partial combustion reactions take place. In the lower section of the reactor, loaded with a high-temperature resistant reforming catalyst, the steam reforming and shift conversion reactions occur as the gas passes through the fixed-bed.
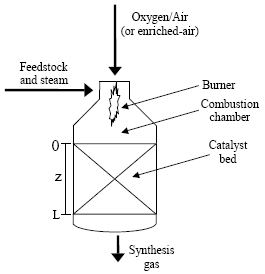
Figure 1: Scheme of a typical ATR unit.
Numerous tests for pilot- and full-scale demonstrations plants at different operating conditions have been reported in the open literature (Christensen and Primdahl, 1994; Aasberg-Petersen et al., 2001). However, there is a lack of modeling and simulation studies about the operation of ATRs. The overall goal of this work is to evaluate the influence of the main operating parameters (e.g., steam-to-carbon ratio, composition of the hydrocarbon feed) on the reactor performance by means of a rigorous mathematical model. The CH4 content, H2/CO, and CO/CO2 ratios at the outlet of the ATR are critical variables as they determine the properties of the produced syngas. The values of these process variables depend on the steam-to-carbon ratio, pressure, inlet and outlet temperatures and the compositions of the feed streams (Christensen et al., 1998).
II. MATHEMATICAL MODEL
A. Chemical Reactions
The ATR of NG (mainly CH4) can be represented by a combination of partial combustion and steam reforming, according to the following reactions.
Combustion zone:
 (1)
(1)
Thermal and Catalytic zones:
 (2)
(2)
 (3)
(3)
 (4)
(4)
The CH4 combustion takes place through numerous radical reactions, but it can be represented as a single molecular reaction, i.e. the highly exothermic combustion to CO and H2O (Eq. 1, Christensen and Primdahl, 1994). The excess CH4, after complete consumption of the O2 in the combustion zone, is further converted by the homogeneous steam reforming (Eqs. 2 and 4) and WGS reaction (Eq. 3) in the thermal zone, which is part of the combustion chamber. Final methane conversion occurs through heterogeneous catalytic reactions (Eq. 2 to 4). The possible occurrence of carbon formation is not considered.
B. Model Equations
The steady-state operation of the ATR is simulated as two reactors in series: combustion zone and catalyst bed. The essential features of these models are described in this section.
B.I. Combustion Chamber
An input-output model, based on global mass and energy balances and equilibrium equations, is selected to describe the upper combustion chamber. Complete oxygen consumption is considered. The occurrence of the homogeneous steam reforming and WGS reactions is taken into account. To this end, a given approach to the equilibrium (Δ Te,SR) is assumed for reaction (2), while the WGS-reaction (3) is supposed to be in equilibrium (Δ Te,WGS =0). The stoichiometric and equilibrium relationships for reactions (1) to (3) are solved together with the enthalpy balance equation to estimate the temperature and composition of the gas mixture that leaves the combustion section. Heat losses to the environment through the wall of the reactor are considered.
B.II. Catalyst Bed
The catalyst bed is represented through a one-dimensional heterogeneous model. The axial dispersion of mass and heat is neglected because of the high gas space velocities. Since the reactor operates under near adiabatic conditions (small heat losses), the radial gradients of temperature and composition are ignored. Due to the high reaction rates on the catalyst surface caused by the high temperature levels, the gas-solid heat-transfer resistance is included in the model (Rostrup-Nielsen, 1993). The strong intraparticle diffusional limitations (Christensen and Primdahl, 1994) are taken into account by rigorous solution of the mass balances inside the catalyst particle, which is assumed isothermal (Raghunandanan and Reddy, 1994). Fresh catalyst conditions are considered. The intrinsic kinetic expressions derived by Xu and Froment (1989) for reactions (2) to (4) are adopted.
Thus, the governing equations for the bulk phase are:
Gas Phase
Mass balances
 | (5) |
 | (6) |
where:
 | (7) |
Energy balance
 | (8) |
Momentum equation
 | (9) |
Boundary conditions
 | (10) |
Catalyst Particle
The selected catalyst particle, Ni/MgAl2O4 spinel, is the industrial Haldor Topsoe RKS-2-7H (tablet-shaped with seven holes and convex ends). The complex geometry of the real particle is represented by means of an equivalent annular model (Piña et al., 2001). The component fluxes on the particle surface, required for the evaluation of the effectiveness factors (Eq. 7) and the heat transferred to the catalyst surface from the bulk gas (first term of the right-hand side of Eq. 8), are obtained by the solution of the following model:
Mass balances
 | (11) |
 | (12) |
Energy balance
 | (13) |
Boundary Conditions:
 | (14) |
C. Numerical Solution
The non-linear algebraic equations that constitute the combustion chamber model are solved by means of a Broyden routine. The differential equations for the gas phase are integrated via a Gear method. The differential equations for the particle are discretized by means of second order finite differences, using an adaptive grid of two elements with variable width. Thirty and ten grid points are assigned to the first (near the catalyst surface) and the second element, respectively. For each axial position, the resultant 89 non-linear algebraic equations are solved through the Broyden algorithm.
D. Model Validation
The model above presented has been checked successfully against data available in the open literature for an industrial H2+CO plant (Christensen and Primdahl, 1994; Aasberg-Petersen et al., 2001). For all the studied experimental conditions the authors reported carbon free operations.
III. RESULTS AND DISCUSSION
To evaluate the capabilities of the proposed model, typical ATRs operating conditions are used (Table 1).
Table 1. Industrial ATR - Reference conditions.

*Christensen and Primdahl, 1994; Aasberg-Petersen et al., 2001.
The estimated value for the gas temperature in the combustion chamber is 1150 oC, within the range reported by Christensen and Primdahl (1994). The calculated values for the temperature and composition of the syngas product, obtained with an approach to the equilibrium for the steam reforming reaction in the combustion chamber Δ Te,SR =326 oC and heat losses of around 2.5% of the total energy generated by partial combustion, are given in Table 1. The CH4 conversion at the outlet of the combustion zone is 80%, with 64 and 16% of the CH4 fed to the ATR being consumed by reactions (1) and (2), respectively. For this reference case, Fig. 2 shows the axial profiles of the gas and solid temperatures in the catalyst bed. The temperatures of both gas and catalyst particle as well as the difference between them decrease along the axial direction. This temperature difference is maximum at the bed inlet (around 45oC at Z =0) as a consequence of the highest heat consumption rate on the catalyst surface. The reforming reaction rates are higher in this zone because both CH4 partial pressure and temperature levels are higher.

Figure 2: Axial profiles of the gas and solid temperatures in the catalyst bed.
Figures 3 and 4 present the composition distributions (gas-phase) and observed reaction rates (2) to (4) along the catalyst bed, respectively.

Figure 3: Mole fraction profiles of each component along the axial distance in the catalyst bed.

Figure 4: Observed reaction rate profiles for reactions (2) to (4) as function of the catalyst bed length.
Most of the CH4 conversion is achieved in the first section of the bed, due to the temperature decrease. The increase in the H2 content is mainly explained by the CH4 reforming to CO (curve  , Fig. 4). The CO2 generation by means of reaction (3) and (4) is not so important (curves
, Fig. 4). The CO2 generation by means of reaction (3) and (4) is not so important (curves  and
and  , Fig. 4). Therefore, the CO/CO2 ratio augments continuously through the catalytic zone. Although the gas that leaves the combustion chamber is assumed to be in equilibrium with respect to the WGS-reaction,
, Fig. 4). Therefore, the CO/CO2 ratio augments continuously through the catalytic zone. Although the gas that leaves the combustion chamber is assumed to be in equilibrium with respect to the WGS-reaction,  is not zero at the bed inlet (Z=0). This behavior is a result of the strong gas-solid heat-transfer resistance. In fact the WGS-reaction rate on the surface of the catalyst particle, which is evaluated at Ts, is slightly positive (r3 at r*=0, Fig. 5). However
is not zero at the bed inlet (Z=0). This behavior is a result of the strong gas-solid heat-transfer resistance. In fact the WGS-reaction rate on the surface of the catalyst particle, which is evaluated at Ts, is slightly positive (r3 at r*=0, Fig. 5). However  and its corresponding effectiveness factor are negative at the bed inlet due to the inversion of the WGS-reaction inside the catalyst particle (Fig. 5). For Z/L> 0.1,
and its corresponding effectiveness factor are negative at the bed inlet due to the inversion of the WGS-reaction inside the catalyst particle (Fig. 5). For Z/L> 0.1,  becomes positive as a consequence of the temperature decrease (Fig. 4). For all the axial positions, the reactions occur in a narrow zone close to the catalyst surface with effectiveness factors in the order of 10-3. This phenomenon is illustrated in Fig. 5 for a particle located at the catalyst bed entrance.
becomes positive as a consequence of the temperature decrease (Fig. 4). For all the axial positions, the reactions occur in a narrow zone close to the catalyst surface with effectiveness factors in the order of 10-3. This phenomenon is illustrated in Fig. 5 for a particle located at the catalyst bed entrance.

Figure 5: Reaction rate profiles for reactions (2) to (4) inside a catalyst particle located at the bed entrance.
A. Influence of the feed composition
The steam-to-carbon ratio (S/C) and the CO2 content in the hydrocarbon stream have been recognized as critical operating parameters (Christensen et al., 1998).
A.I. Steam-to-carbon ratio (S/C)
To simulate situations where the S/C ratio is varied, the steam flowrate has been modified from the value of the reference case (Table 1). To keep constant the gas temperature at the reactor outlet (TL=950 oC), the oxygen-to-carbon ratio (O2/C) has been simultaneously adapted (Fig. 6). Figure 6 also shows that lower S/C ratios give a syngas with lower H2/CO and higher CO/CO2 ratios. These trends are in agreement with the experimental data reported by Christensen and Primdahl (1994) and Christensen et al. (1998).

Figure 6: Effect of S/C on H2/CO and CO/CO2 product ratios. Adjustment of O2/C to keep TL=950 oC. Δ Te,SR =326 oC and Δ Te,WGS =0 oC.
Figure 7 displays the gas temperature axial profiles in the catalyst bed, for three different S/C ratios. The higher the S/C ratio, the lower is the temperature drop along the catalytic zone (TL-T0) due to the lower CH4 partial pressures at the outlet of the combustion chamber (i.e., higher CH4 and energy consumption by the homogeneous reactions 2 to 4).

Figure 7: Gas temperature axial profiles for different S/C. TL=950 oC, Δ Te,SR =326 oC and Δ Te,WGS =0 oC.
A.II. Carbon dioxide-to-carbon ratio (CO2/C)
Different CO2/C ratios have been selected to study the effect of the feed composition on the ATR performance. The feed gas molar flowrate (Fgas) has been kept constant by decreasing the S/C ratio. The CO2/C and O2/C ratios have been simultaneously varied to maintain the outlet gas temperature at 950 oC (Fig. 8). As it can be seen in Fig. 8, higher CO2/C ratios lead to a product gas with lower H2/CO and CO/CO2 ratios. The simulation results are consistent with the pilot plant tests performed by Christensen et al. (1998).

Figure 8: Effect of CO2/C on H2/CO and CO/CO2 product ratios. Adjustment of O2/C to keep TL=950 oC. Fgas=3500 Nm3/h, Δ Te,SR =326 oC and Δ Te,WGS =0 oC.
Figure 9 shows the WGS observed reaction rate for different CO2/C ratios along the catalyst bed. Due to the higher CO2 contents, the WGS-reaction proceeds reverse ( 0) in higher fractions of the total length.
0) in higher fractions of the total length.
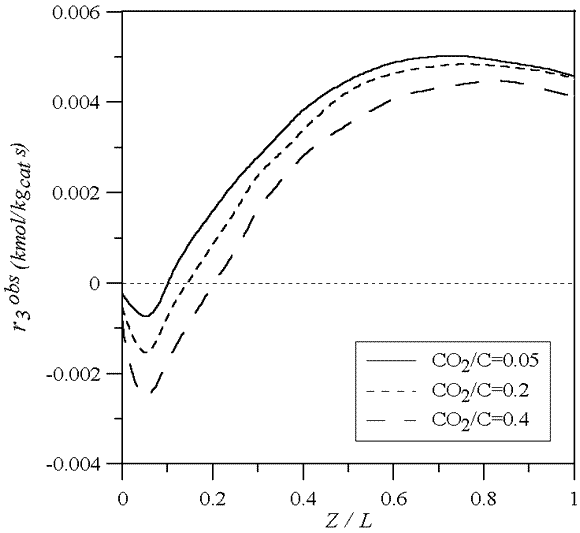
Figure 9: WGS observed reaction rate axial profile in the catalyst bed for different CO2/C. Fgas=3500 Nm3/h, TL=950 oC, Δ Te,SR =326 oC and Δ Te,WGS =0 oC.
B. Influence of the extents of the homogeneous reactions in the combustion chamber
Several experimental data for industrial and pilot scale ATRs are reported in the literature (Christensen and Primdahl, 1994; Christensen et al., 1998; Aasberg-Petersen et al., 2001). However there is a lack of information about the composition and temperature of the gas leaving the combustion chamber. This fact does not allow to validate the model assumptions for the combustion chamber, introducing uncertainties in the prediction of the inlet conditions to the catalyst bed. To analyze the influence of the assumed extents for the homogeneous reactions in the combustion zone, the reference case presented in Table 1 has been chosen.
B.1. Extent of the homogeneous methane reforming
The Δ Te,SR and the percentage of heat loss with respect to the total energy generated by partial combustion (Qloss/Qcomb) have been simultaneously varied to keep constant the outlet temperature (TL curve, Fig. 10). The gas temperatures at the outlet of the combustion chamber (T0), as well as the temperature at which the equilibrium of reaction (2) is evaluated in the combustion zone (Te,SR), are also shown in Fig. 10 for different Δ Te,SR.

Figure 10: Effect of Δ Te,SR on Te,SR, T0 and TL. Adjustment of Qloss/Qcomb to keep TL=950 oC.
As expected, lower extents of the homogeneous reaction (2) (i.e., higher Δ Te,SR values) lead to higher temperatures and lower CH4 conversions in the combustion chamber (T0 and xCH4,0 in Fig. 10 and 11, respectively). The total methane conversion (xCH4,L) is almost unchanged due to the assumption of constant TL. However as Δ Te,SR is augmented, the H2/CO and CO/CO2 ratios in the product decrease and increase respectively.

Figure 11: Effect of Δ Te,SR on xCH4,0, xCH4,L, H2/CO and CO/CO2 product ratios for TL=950 oC.
B.2. Extent of the homogeneous WGS-reaction
To study the effect of the homogeneous WGS-reaction on the ATR operation, the reference case has been simulated for different Δ Te,WGS, at constant Δ Te,SR and Qloss/Qcomb. The methane conversions at the outlet of the combustion chamber and catalyst bed (xCH4,0 and xCH4,L) are almost independent of Δ Te,WGS as a result of the lower reaction enthalpy of the WGS-reaction in comparison with the reaction enthalpy of the partial combustion and steam reforming reactions (Fig. 12). Even though the extent of the WGS-reaction in the combustion chamber diminishes as Δ Te,WGS is augmented, the H2/CO and CO/CO2 product ratios increase and decrease, respectively (Fig. 12). This behavior is a consequence of the higher extent of the WGS-reaction in the catalyst bed. In this zone, the gas temperature levels for different Δ Te,WGS are very similar but the CO partial pressure increases with Δ Te,WGS.

Figure 12: Effect of Δ Te,WGS on xCH4,0, xCH4,L, H2/CO and CO/CO2 product ratios for TL=950 oC. Δ Te,SR =326 oC and Qloss/Qcomb=2.5 %.
The curves shown in Figs. 11 and 12 can be used to estimate appropriate values of the unknown variables Δ Te, SR and Δ Te,WGS from experimental data of H2/CO and CO/CO2 ratios in the product stream.
IV. CONCLUSIONS
A detailed mathematical model to simulate the operation of industrial ATRs has been presented. The model predicts the temperature and composition of the gas that leaves the combustion chamber, the temperature and concentration profiles along the catalyst bed and the concentration gradients inside the catalyst particle. Significant temperature differences between bulk gas and catalyst surface and strong intraparticle diffusional limitations have been found, demonstrating the need for taking into account these heat- and mass-transfer resistances. Measurements of the gas temperature at the outlet of the combustion chamber would help in the task of determining the real extents of each of the homogeneous reaction (2) to (4) in the thermal zone. The proposed model is a useful tool to identify critical operating parameters and analyze their influence on the performance of autothermal reforming units.
NOMENCLATURE
av = particle surface area per unit reactor volume (mcat2/mr3).
cp = heat capacity of the process gas, (kJ/kg K).
Dje = effective diffusivity of comp. j, (m2/s).
dp = equivalent particle diameter, (m).
f = friction factor.
Fj = molar flowrate of component j, (kmol/s).
g = acceleration of gravity, (m/s2).
Δ Hi= heat of reaction i, i=2,3,4 (kJ/kmol).
hf = solid-gas heat-transfer coefficient, (kJ/m2s).
L = reactor length, (m).
pj = partial pressure of comp. j (gas phase), (bar).
ps,j = partial pressure of comp. j inside the catalyst, (bar).
pt = total pressure, (bar).
Qloss,bed = heat loss per unit length at z, (kJ/s m).
r = radial coordinate of the catalyst particle, (mcat).
R = universal gas constant, (kJ/kmol K).
r* = [(r-rin)/(req-rin)].
req = outer radius of the equivalent particle, (mcat)
ri = rate of the reaction i, (kmol/kgcats).
rin = inner radius of the equivalent particle, (mcat).
riobs = observed reaction rate for reaction i, (kmol/kgcats).
T = gas temperature, (K).
Ts= solid temperature, (K)
us = superficial velocity, (mf3/mr2 s).
V =volume of the catalyst particle, (mcat3).
xCH4 = methane conversion.
xCO2 = conversion of CH4 into CO2, [(FCO2-FCO2,0)/FCH4,0].
yj = molar fraction of component j.
z = axial coordinate, (m).
Greek letters
η; i= effectiveness factor for reaction i, i= 2,3,4.
ρ B = bed density,(kgcat/mr3).
ρ g = gas density, (kg/mf3).
ρ p= catalyst particle density, (kgcat/mcat3).
Ω = cross section of the catalyst bed, (mr2).
Subscripts
0 = at the catalyst bed inlet.
L = at the catalyst bed outlet.
Superscripts
s = at the catalyst particle surface.
AKNOWLEDGEMENTS
The authors are grateful to CONICET (Argentina) for the financial support during the work.
REFERENCES
1. Aasberg-Petersen, K., Bak-Hansen, J., Christensen, T., Dybkjaer, I., Seier Christensen, P., Stub Nielsen, C., Winter Madsen, S., Rostrup-Nielsen, J., "Technologies for Large Scale Conversion", Applied Catalysis A General, 221, 379-387, (2001). [ Links ]
2. Christensen, T., Primdahl, I., "Improve Syngas Production using Autothermal Reforming", Hydrocabon Processing, March (1994). [ Links ]
3. Christensen, T., Christensen, P., Dybkjaer, I., Bak-Hansen, J., Primdahl, I., "Developments in Autothermal Reforming", Stud. Surf. Sci. Cat., 119, 883-888, (1998). [ Links ]
4. Dybkjaer, I., Christensen, T., "Syngas for Large Scale Conversion of Natural Gas to Liquid Fuels", Stud. Surf. Sci. Cat., 435-440, (2001). [ Links ]
5. Piña, J., Schbib, S., Bucalá, V., Borio, D., "Influence of the Heat-flux Profiles on the Operation of Primary Steam Reformers", Ind. & Eng. Chem. Res., 40, 5215-5221, (2001). [ Links ]
6. Raghunandanan, K., Reddy, K., "Development of a Mathematical Model for Secondary Reformers", Chem. Eng. Technol., 17, 273-279, (1994). [ Links ]
7. Rostrup-Nielsen, J., "Steam Reforming Opportunities and Limits of the Technology", Catalysis Today, 18, 305-324, (1993). [ Links ]
8. Xu, J., Froment, G., "Methane Steam Reforming, Methanation and Water-Gas Shift I: Intrinsic Kinetics", AIChE J., 35, 88-96, (1989). [ Links ]
Received: December 14, 2005.
Accepted for publication: June 20, 2006.
Recommended by Editor A. Bandoni.














