Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.36 n.4 Bahía Blanca oct./dic. 2006
A mathematical model for the styrene - methyl methacrylate copolymerization in the presence of polybutadiene
C. G. Gutierrez, D. A. Estenoz, L. M. Gugliotta, J. R. Vega and G. R. Meira
INTEC - Univ. Nacional del Litoral - CONICET, Güemes 3450, 3000 Santa Fe, Argentina.
lgug@intec.unl.edu.ar
Abstract — The batch copolymerization of styrene (St) and methyl methacrylate (MMA) in the presence of polybutadiene (PB) is theoretically and experimentally investigated. A mathematical model that enables to calculate the main global variables and the macromolecular structure of the evolving polymer mixture is presented. The model is an extension of that developed by Estenoz et al. (1999) for the homopolymerization of St in the presence of PB. It was validated with experiments that considered diluted solution and bulk copolymerizations carried out at a constant low temperature (65 o C), with THF as solvent, benzoyl peroxide as initiator, and a St-MMA ratio close to the azeotropic composition. For comparison, the solution copolymerization without PB was also considered. All experimental runs were adequately simulated using a single set of kinetic parameters.
Keywords — Graft Copolymerization. Mathematical Modeling. MBS.
I. INTRODUCTION
Several heterogeneous polymers used as high-impact resistant materials contain rubber particles dispersed in a vitreous matrix. Examples of such composite materials are ABS: polymer of acrylonitrile, butadiene (B), and styrene (St); HIPS: high impact polystyrene (PS); and MBS: polymer of methyl methacrylate (MMA), B, and St. In particular, MBS is normally employed as an impact modifier polymer (e.g., in PVC formulations).
From the macromolecular point of view, MBS is a mixture of a linear free copolymer (FC) of St-MMA, a linear unreacted polybutadiene (PB), and a graft terpolymer (GT) constituted by St-MMA branches linked onto PB chains. MBS can be produced by solution, bulk or emulsion copolymerization of St and MMA in the presence of PB.
The bulk and solution copolymerizations of St-MMA have been extensively studied. In particular, Kuo and Chen (1981) considered the copolymerization of St and MMA at its azeotropic composition. For such processes, well-known mathematical models have been developed (see Gao and Penlidis, 1998). As far as the authors are aware, the mathematical modeling of the free-radical copolymerization of St and MMA in the presence of PB, for the production of MBS, has not yet been considered.
In this work, a mathematical model is developed for the solution or bulk copolymerization of St and MMA in the presence of PB. The model is an extension of that developed by Estenoz et al. (1999), and it was adjusted on the basis of three isothermal reactions. The model estimates the main global variables (conversion, copolymer composition, and grafting efficiencies), and the macromolecular structure of both the FC, and the unreacted PB.
II. MATHEMATICAL MODEL
Consider the global kinetic mechanism of Table 1. It considers chemical and thermal initiation, propagation, transfers to the comonomers and to the rubber, and terminations by combination and by disproportionation. According to this mechanism, grafting chains are produced by attack of a primary initiator radical onto PB, or by transfer reactions to the rubber. The following nomenclature is adopted: S and M represent the St and MMA monomers, respectively;  and
and 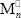 are radicals with n repetitive units terminated in St and MMA, respectively; Cn is a FC molecule containing n repetitive units; T is a terpolymer (or a PB) molecule with at least one unreacted B unit;
are radicals with n repetitive units terminated in St and MMA, respectively; Cn is a FC molecule containing n repetitive units; T is a terpolymer (or a PB) molecule with at least one unreacted B unit;  is a rubber primary radical generated on the initial PB or on the GT;
is a rubber primary radical generated on the initial PB or on the GT; 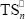 and
and  are terpolymer non-primary radicals with n repetitive units in their active chains terminated in St and MMA, respectively.
are terpolymer non-primary radicals with n repetitive units in their active chains terminated in St and MMA, respectively.
The following assumptions are adopted: a) the radical reactivity only depends on the terminal unit, and the reactivity of a primary monomeric radical coincides with that of a generic radical; b) the rates of propagation, chain transfer, and termination are independent of chain length; c) the termination reactions are diffusion controlled (gel effect); d) all the unreacted B units exhibit the same reactivity; e) the propagation with the internal double bonds, the intramolecular termination, the intramolecular transfer (or backbiting), the oxidation, and the degradation reactions are all neglected; and f) pseudo-rate constants are used for calculating the macromolecular structure, that consider the FC and the copolymer branches as pseudo-homopolymers.
Table 1: Global Kinetic Mechanism
From the kinetic mechanism of Table 1, and assuming an homogeneous process with a constant reaction volume, V, the mathematical model of the Appendix was derived. It allows the calculation of: a) the global concentrations; b) the conversion, x; c) the mass fraction of St in the FC,  ; d) the monomer grafting efficiency, E (defined as the ratio between the mass of grafted monomers and the total mass of polymerized monomers); e) the PB grafting efficiency, EPB (defined as the ratio between the mass of grafted PB and the initial PB mass); f) the number- and weight-chain length distributions (NCLD and WCLD) for the FC and for the unreacted PB; and g) the number- and weight-average molecular weights,
; d) the monomer grafting efficiency, E (defined as the ratio between the mass of grafted monomers and the total mass of polymerized monomers); e) the PB grafting efficiency, EPB (defined as the ratio between the mass of grafted PB and the initial PB mass); f) the number- and weight-chain length distributions (NCLD and WCLD) for the FC and for the unreacted PB; and g) the number- and weight-average molecular weights,  and
and 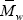 for the FC and for the unreacted PB.
for the FC and for the unreacted PB.
III. EXPERIMENTAL WORK
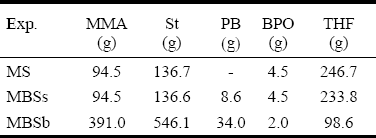
Three batch copolymerizations of St-MMA were carried out under isothermal conditions (at 65 o C) and at the azeotropic comonomers ratio. The recipes are given in Table 2. The experiments involved both diluted solution and bulk reactions. The solution polymerizations were carried out either in absence of PB (experiment MS), or in presence of PB (experiment MBSs). The bulk copolymerization was carried out in presence of PB (experiment MBSb). In all reactions, benzoyl peroxide (BPO) was used as initiator, and tetrahydrofurane (THF) as solvent. The solution copolymerizations were carried out in a conventional 500 mL three-neck Pyrex reactor. For the bulk reaction, a stainless-steel stirred-tank reactor was used. Samples were withdrawn along the polymerizations and the reactions were "shortstopped" after 8 hrs. The PB was assumed linear, and its molecular weight distribution (MWD) was determined by size exclusion chromatography (SEC). The average molecular weights resulted: 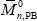 = 101,900 g/mol, and
= 101,900 g/mol, and 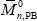 = 218,200 g/mol.
= 218,200 g/mol.
Table 2: Polymerization Recipes
The reaction samples were analyzed to determine: a) x, E, and EPB, by gravimetry; b)  ,
, 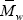 (for the FC and for the unreacted PB) by SEC; and c)
(for the FC and for the unreacted PB) by SEC; and c)  by SEC and by UV-vis spectroscopy at 260 nm.
by SEC and by UV-vis spectroscopy at 260 nm.
For the SEC analyses, a Waters 1515 chromagraph was used with a complete set of 6 μ-Styragel columns, a Waters 410 differential refractometer (DR) and a Waters 440 UV spectrophotometer (at 254 nm). The solvent was THF at 1 mL/min.
The monomer conversion and the grafting efficiencies were determined gravimetrically after separation by solvent extraction techniques. First, the solvent and the unreacted monomers were eliminated under vacuum at room temperature until constant weight, and the total polymer mass was determined. Then, the monomer conversion was calculated by subtraction of the original PB mass. The FC was extracted from approximately 0.3 g of the total dry polymer, as follows: a) 10 mL of methyl ethyl ketone (MEK) were added to the polymer; b) the mixture was agitated for 12 hrs in a centrifuge tube, and then was centrifuged for 2 hrs at 10000 rpm; c) the soluble portion was separated by decantation; d) 10 mL of MEK were added into the insoluble fraction, and the procedure was repeated; e) the two copolymer solutions were mixed together, the total copolymer was precipitated with methanol and dried until constant weight; f) the insoluble fraction in the centrifuge tube was dried under vacuum until constant weight, and the insoluble mass (i.e.: the GT + the unreacted PB) was determined; g) the grafted monomer mass was obtained from the difference between the insoluble mass and the initial PB mass; and h) the monomer grafting efficiency was obtained from the ratio between the grafted and the total bound monomer mass.
The unreacted PB mass and the PB grafting efficiency were determined through a second solvent extraction procedure applied to the precipitate of GT and unreacted PB. Petroleum ether dissolves the unreacted PB, but it does not dissolve the GT. First, 10 mL of petroleum ether were added to the precipitate, and the mixture was agitated and centrifuged. The soluble portion was isolated from the GT, and the procedure was repeated twice. The PB solutions were mixed together, and the unreacted PB was isolated by solvent evaporation. The mass of grafted PB was determined from the difference between the initial PB mass and the unreacted PB mass. Finally, inconclusive verification of the solvent fractionation procedure was obtained by thin layer chromatography of the isolated polymer fractions.
In Fig. 1, the measured variables are shown (in symbols). The final product characteristics are presented in Table 3.
IV. PARAMETER ADJUSTMENT AND SIMULATION RESULTS
Most of the model parameters were taken from literature. Some parameters were adjusted to fit the experimental values, with the following criterion: a) the homopropagation constants, kpSS and kpMM, to fit x; and b) the rate constants of initiation and transfer to the rubber, ki2, kfgS, and kfgM, to fit E. The resulting model parameters are shown in Table 4.
Equations (A.1)-(A.10) were solved by standard numerical methods for "stiff" differential equations. For the calculation of the WCLDs, Eqs. (A.27) and (A.29) were calculated as discrete distributions and many molecular species were lumped together at fixed chain-length intervals (Δn = 50, for the FC and Δn = 180 for the PB). The final number of differential equations were 1000 for the FC, and 400 for the PB. Typically, 3 sec were required to simulate the process in a standard PC.
In Table 3 and Fig. 1, the measured variables are compared with the theoretical predictions, and in general a quite reasonable agreement is observed. The PB has a negligible effect on conversion (Fig. 1a). The monomer grafting efficiency is approximately constant along the reaction, and the final values are higher than 20% (Fig. 1b). The predicted St mass fraction in the FC is constant and close to the azeotropic value (Fig. 1c). The dispersion of the experimental composition measurements around the azeotrope is probably due to contamination of the FC with PB or GT. As expected, the average molecular weights of the FC are higher in the bulk reaction, due to the gel effect (Fig. 1d-f). A slight decrease of the molecular weights is observed in the dilute solution reactions, due to the lower initiator consumption with respect to the monomer consumption (Fig. 1d, e).
In Fig. 2, some additional results for the bulk experiment are presented. The PB graft efficiency increases along the reaction, reaching a final value of about 76% (Fig. 2a). As expected, the average molecular weights of the unreacted PB decrease along the polymerization. The steeper decrease observed in 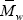 with respect to
with respect to  (Fig. 2b) is due to the higher grafting probability of the longer PB chains. The higher experimental molecular weights with respect to the model predictions may be due to a contamination by GT.
(Fig. 2b) is due to the higher grafting probability of the longer PB chains. The higher experimental molecular weights with respect to the model predictions may be due to a contamination by GT.
Figure 1: Comparison between model predictions (in continuous traces) and experimental results (in symbols). a) Gravimetric conversion, b) monomers grafting efficiency, c) mass fraction of St in the FC (average values of UV-Vis spectroscopy and SEC measurements), and d), e), f) evolution of the number- and weight-average molecular weights of FC for experiments MS, MBSs and MBSb, respectively.
Table 3: Measurements (upper value) and Theoretical Predictions (lower value, in parentheses)
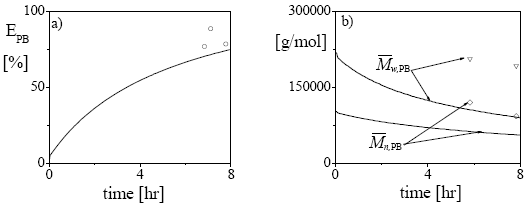
Figure 2: Experiment MBSb: Comparison between the model predictions (in continuous trace) and the experimental values (in symbols) of: a) grafting efficiency of PB, b) average molecular weights of the unreacted PB.
Table 4: Adopted Kinetics Parameters (at 65o C)
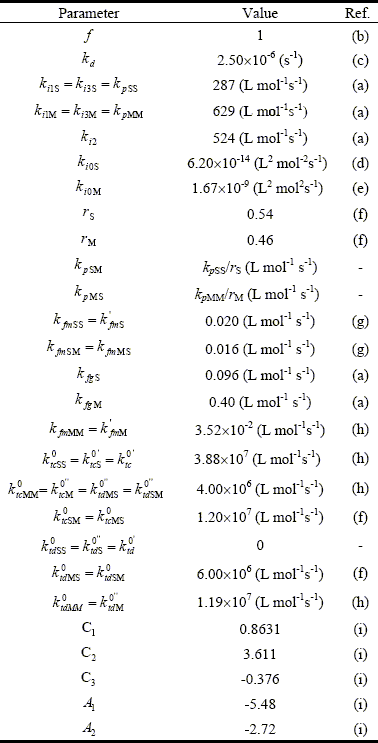
(a) Adjusted in this work; (b) Louie et al. (1985); (c) van Herk (2000); (d) Peng (1990); (e) Lignau et al. (1979); (f) Kuo and Chen (1981); (g) Schoonbrood et al. (1996); (h) Brandrup et al. II/89 (1999); (i) Friis and Hamielec, (1975).
V. CONCLUSIONS
This work constitutes a first attempt for estimating the main reaction variables and molecular characteristics of MBS obtained by a solution or a bulk copolymerization of St and MMA in presence of PB. A mathematical model was developed for simulating the batch bulk and solution processes, and it adequately estimates the observed evolutions of main reaction variables.
Even though 3 experiments have been only presented, the model was also verified with experimental data from homopolymerizations of either St or MMA in the presence (and in the absence) of PB.
The model will be further extended for predicting the detailed macromolecular structure of the GT, and for simulating an industrial MBS process.
Appendix: Polymerization Model
From the kinetics of Table 1, the mass balances for the initiator (I2), the St (S), the MMA (M), the B units in the PB (B*), and the main radical species result:
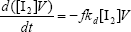 | (A.1) |
 | (A.2) |
 | (A.3) |
 | (A.4) |
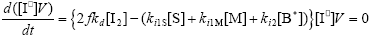 | (A.5) |
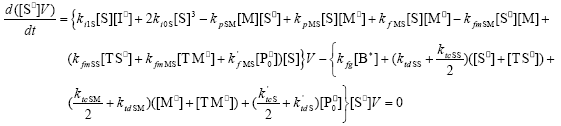 | (A.6) |
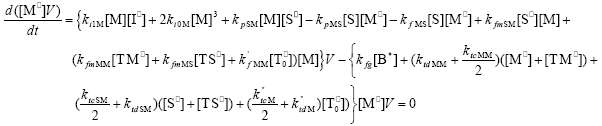 | (A.7) |
 | (A.8) |
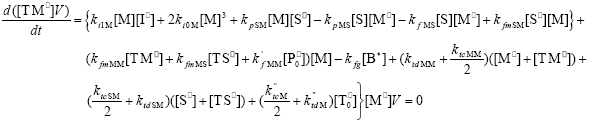 | (A.9) |
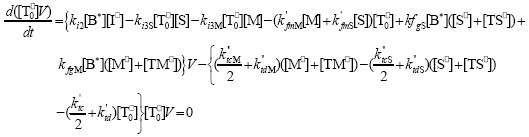 | (A.10) |
where 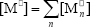 ,
,  ,
, 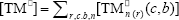 ,
, 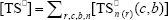 ,
, 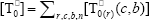 , r is the number of trifunctional grafting points per molecule¸ c, b respectively represent the number of comonomer repetitive units and B repetitive units, and n is the number of comonomer repetitive units in the active branches.
, r is the number of trifunctional grafting points per molecule¸ c, b respectively represent the number of comonomer repetitive units and B repetitive units, and n is the number of comonomer repetitive units in the active branches.
The WCLDs for the free copolymer [indicated by GFC(n)] is calculated from the following mass balances for each of the accumulated copolymer species:
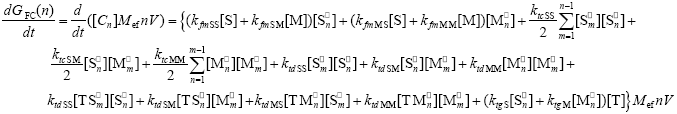 | (A.11) |
In Eq. (A.11), the effective molecular weight for the equivalent monomeric unit is defined as:
 | (A.12) |
To derive an analytical expression for the WCLD of FC from Eq. (A.11), the following dimensionless kinetic parameters are defined:
 | (A.13) |
 | (A.14) |
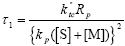 | (A.15) |
 | (A.16) |
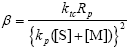 | (A.17) |
| α = τ + β | (A.18) |
where
 | (A.19) |
and the pseudo kinetic homopolymerization constants are calculated through:
 | (A.20) |
 | (A.21) |
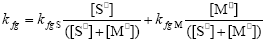 | (A.22) |
 | (A.23) |
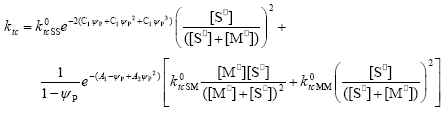 | (A.24) |
 | (A.25) |
 | (A.26) |
In Eqs. (A.23) - (A.26) the expressions for the diffusion controlled termination coefficients proposed by Friis and Hamielec (1975) have been included, where ψp represents the polymer volume fraction.
By introducing Eqs. (A.13)-(A.26) into Eq. (A.11) and operating as in Estenoz et al. (1999), the following expression for the WCLD of the FC can be obtained:
 | n = 1, 2, 3, 4 ...... | (A.27) |
Finally, the WCLD of the unreacted PB [GPB(n)] can be derived from the mass balances of each PB species:
 | n = 1, 2, 3 ...... | (A.28) |
where NPB(n) represents the total moles of the PB specie with chain length n. Then, by considering Eqs. (A.13)-(A.26) into Eq. (A.28), the WCLD for the unreacted PB results:
 | n = 1, 2 ,3 .... | (A.29) |
Global Derived Variables
From the resolution of previous balances, the following output variables can be calculated:
Monomer Conversion
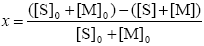 | (A.30) |
where the subscript '0' indicates initial conditions.
Monomer Grafting Efficiency
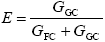 | (A.31) |
where GGC and GFC are the total monomer masses accumulated in the GT and FC, respectively, calculated as:
 | (A.32) |
 | (A.33) |
PB Grafting Efficiency
 | (A.34) |
where  is the initial PB mass; and GPB is the unreacted PB mass, calculated from:
is the initial PB mass; and GPB is the unreacted PB mass, calculated from: 
Average Molecular Weights of the FC and of the Unreacted PB
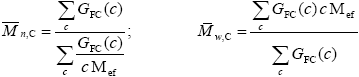 | (A.35) |
 | (A.36) |
Mass Fraction of St in the FC
Finally, by assuming that the grafted St-MMA branches and the FC have the same St composition, the following expression is used to estimate the mass fraction of St in the FC:
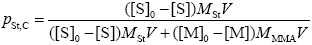 | (A.37) |
REFERENCES
1. Brandrup, J., E. H. Immergut and E. A. Grulke, Polymer Handbook, 4th Ed., Wiley, New York (1999). [ Links ]
2. Estenoz, D.A., I. M. González, H. M. Oliva and G. R. Meira, "Polymerization of styrene in presence of Polybutadiene. Determination of the molecular structure", J. Appl. Polym Sci., 74, 1950-1961 (1999). [ Links ]
3. Friis, N. and A. C. Hamielec, "Gel-effect in emulsion polymerization of vinyl monomers", ACS Polymer Preprints, Polym. Chem. 16 (1), 192-197 (1975). [ Links ]
4. Gao, J. and A. Penlidis, "A comprehensive simulator/database package for reviewing free-radical copolymerizations", J. M. S.-Rev. Macromol. Chem. Phys., C38 (4), 651-780 (1998). [ Links ]
5. Kuo, J. and C. Chen, "Studies on radical chain copolymerization of methyl methacrylate and styrene at their azeotropic composition", Macromol., 14, 335-339 (1981). [ Links ]
6. Lignau, J., M. Stickler and G. Meyerhoff; "The spontaneous polymerization of methyl methacrylate-IV. Formation of cyclic dimers and linear trimers", Eur. Polymer J., 16, 785-791 (1979). [ Links ]
7. Louie, B. M., G. M. Carrat and D. S. Soong, "Modeling the free radical solution and bulk polymerization of methyl methacrylate", J. of Appl. Polym. Sci., 30, 3985-4012 (1985). [ Links ]
8. Peng, F. M., "Polybutadiene grafting and crosslinking in high-impact polystyrene bulk thermal process", J. Appl. Polym. Sci., 40 (7-8), 1289-1302 (1990). [ Links ]
9. Schoonbrood, H., S. Pierik, B. van den Reijen, J. Heuts and A. German, "Cross-chain transfer rate constants of styrene-terminated radicals to methyl acrylate and methyl methacrylate", Macromol., 29, 6717-6723 (1996). [ Links ]
10. van Herk, A.M., "Pulsed initiation polymerization as a means of obtaining propagation rate coefficients in free-radical polymerizations. Review up to 2000", Macromol. Theory Simul., 9(8), 433-441 (2000). [ Links ]
Received: December 20, 2005.
Accepted for publication: July 21, 2006.
Recommended by Editor A. Bandoni.














