Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.37 n.1 Bahía Blanca ene. 2007
Real-time disparity map extraction in a dual head stereo vision system
G. Calin1 and V. O. Roda1
1 Escola de Engenharia de São Carlos, Universidade de São Paulo, São Carlos, Brazil
gcalin@uol.com.br, valentin@sel.eesc.usp.br
Abstract — This paper describes the design of an algorithm for constructing dense disparity maps using the image streams from two CMOS camera sensors. The proposed algorithm extracts information from the images based on correlation and uses the epipolar constraint. For real-time performance, the processing structure of the algorithm was built targeting implementation on programmable logic, where pipelined structures and condensed logic blocks were used.
Keywords — Stereo Vision. Disparity Map. Programmable Logic.
I. INTRODUCTION
Researchers have been giving especial attention to computer vision systems capable of delivering accurate 3D information of an observed scene, which leads to the construction of robust intelligent vehicles. Using low cost sensors, it has been possible to develop stereo vision systems capable of extracting 3D features by passive sensing of the environment.
Most stereo vision implementations are based on a two camera configuration setup, where each camera delivers a two 2D representation of a given scene, as show in Fig. 1. Stereo vision is achieved by extracting 3D information by processing two or more 2D images of a given scene. The processing for extracting the 3D information creates a map that describes which point in the 2D images corresponds to the same point in the 3D scene. Detailed description of the stereo vision problem has been widely studied in past and it is not presented. Refer, for instance, to Grosso et al. (1989) and Grosso and Tistarelli (1995) for a detailed study of this subject.

Figure 1. Typical Stereo Vision problem: two cameras, acquiring images of the same scene, have two different 2D representation of a common 3D point. With proper processing, the position and depth of the 3D point can be extracted from the images
Several stereo algorithms have been proposed in recent years to solve the problem of finding the correspondence of the right and left image. Simple methods employ the measure of absolute or squared differences of the pixels intensities, to measure the similarity between the images (Sunyoto et al., 2004). Other methods, in order to increase accuracy, employ window-based matching, where a cost function is evaluated around the pixel of interest to find the best match. These methods usually do not consider occlusions and present problems in regions displaying little or repetitive textures, leading to similar cost functions and being unable to find the proper match (Darabiha et al., 2003; Silva et al., 2003; Cox et al., 1996).
Birchfield and Tomasi (1998a, b) employed dynamic programming to solve the matching problem, where each scanline -and in some cases in-between scanlines- are described as a dynamic cost function and evaluated with addition of some penalties criteria, like occlusions and large jumps in disparity.
II. PROPOSED METHOD
The proposed method employs a windows-based matching technique to find the disparity map on a pair of stereo images. Similar solutions were proposed in many past papers and represent a simple solution to the matching problem. Although it presents some known limitations, as being unable to process occlusions and large disparity jumps, the windows-based matching technique was chosen and used as base for this study due its potential of being ported to a small Field-Programmable Gate Array (FPGA) device.
For the proposed system, Fe and Fd denote the left and right frames from the CMOS camera sensors, located respectively at right and left sides of the scene. The source frame is w pixels large and of h pixels height, with 8-bit grayscale intensities.
The video frames Fe and Fd are addressed as vectors,  and
and 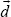 of (w · h) length, where the first vector position stores the intensity of the upper-left pixel and the last position stores the bottom-right pixel intensity.
of (w · h) length, where the first vector position stores the intensity of the upper-left pixel and the last position stores the bottom-right pixel intensity.
Ie(k) and Id(k) is the intensity of a given pixel k located respectively in vectors  and
and 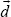 , where k ∈ {0, 1, ..., (w · h) - 1}.
, where k ∈ {0, 1, ..., (w · h) - 1}.
The parameter ω is defined as the window width and β the observation region around pixel k, as shown in Figure 2.

Figure 2. Windows based match. A windows around pixel k in the  vector is compared with 2β windows in vector
vector is compared with 2β windows in vector 
In Eq. (1) the similarity function S(j) is defined. This function measures the squared distance from a window in vector  (centered in a given pixel k) and a window in vector
(centered in a given pixel k) and a window in vector 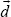 , displaced by j pixels.
, displaced by j pixels.
 | (1) |
where i ∈ Z, ω ∈ {1, 3, 5, 7, ...}
C(k), defined in Eq. (2), returns the best match (minimum distance) for a given window centered in pixel k, when compared with 2β windows in vector 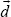 .
.
 | (2) |
Since only a limited number of pixels are need for the matching process, vectors  and
and 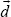 can be trimmed to reduce the memory allocation.
can be trimmed to reduce the memory allocation.
III. DESIGN OF A STEREO VISION SYSTEM
In this paper, for parallel, efficient and condensed hardware implementation of the proposed algorithm, some constrains have been included: 1) CMOS camera sensors with digital interface were used, avoiding implementation of a video interface to digitalize signals from a regular analog video camera; 2) The parameters ω and β were fixed, based in the results of the simulations and camera setup (typically ω = 11 and β = 4 were used). This allowed a small use of resources, since just a small number of pixels must be present for processing; 3) External memory was used only for storing the final processed disparity map (for debugging purposes).
Also the simplicity of the formulation allowed implementation of all elemental functions with available in-hardware math blocks or by creating simple logic constructions, such as subtraction and magnitude comparison blocks.
A. Pipeline Structure
The developed architecture of the stereo vision system is illustrated in Fig. 3. It consists of a five stage pipeline process capable of processing 160x120 pixels grayscale frames at video rate speed (30 frames/s). Each new pixel, delivered by the cameras, moves the pipeline forward, creating a FIFO process at pixel-rate speed. This allowed a very condensed implementation in terms of logic allocation and memory, and the possibility for future addition of other post-processing algorithms.

Figure 3. Pipeline structure used to process the proposed stereo vision algorithm
Higher clocks frequencies were used to allow execution of machine states within a pixel-rate period. This was needed because some processes could not be parallelized in hardware and needed to be executed in sequential order.
B. Pipeline Stages
In pipeline stage 1, vectors  and
and 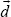 allocate limited memory, since a small history of pixels is needed to process the disparity. In the first pipeline state every new pixel available by the cameras are shifted in the vectors, and the oldest pixel is discarded. This process occurs in two steps, first shifting the vectors and then adding the new available pixels.
allocate limited memory, since a small history of pixels is needed to process the disparity. In the first pipeline state every new pixel available by the cameras are shifted in the vectors, and the oldest pixel is discarded. This process occurs in two steps, first shifting the vectors and then adding the new available pixels.
Stage 2 is responsible for measuring the all pixel distance from the two vectors, making data available for computing the squared distance in stage 3.
Stage 3 employs hardware multipliers to compute the square function of all data processed in state 2. Since only a limited number of multipliers are available, this stage was broken in several small processes.
Stage 4 computes the sum function for every compared window. This results in a set of data representing the cost function.
Stage 5 uses a tree comparison structure to analyze the data from stage 4. The minimum distance is detected and a disparity coefficient is assigned.
C. Pipeline Structure evaluation
Prior to hardware implementation, the pipeline structure was tested and evaluated using custom developed software. Delphi development platform was used due its facilities to emulate low-level binary processes and possibility to quick output results in graphic form for analysis.

Figure 4. Custom software interface used to evaluate he presented pipeline structure prior to hardware implementation
The results obtained by software emulation were very important during hardware implementation, allowing quick comparison of results and identification of hardware programming errors.
D. Hardware
To test the algorithm, a Xilinx Spartan-3 development board was used. This board uses a Spartan-3 FPGA (model XC3S200), a low-cost FPGA, with 200k logic blocks and twelve 18-bit hardware multipliers.

Figure 5. Hardware setup, including the Xilinx FPGA development board and the two CMOS cameras.
A base clock of 50MHz was used for synthesizing all required system clocks.
To acquire the images, a pair of low cost OmniVision CMOS sensor were used. Two web-cams were disassembled and its image sensors wired to obtain the raw digital data, at video-rate speed.
Employed OminiVision sensors (model OV7648) were able to delivery frames in digital format (160x120 pixels 8-bit grayscale) at required frame rate (30 frames/s).
In addition a serial interface was build for debugging purposes. The processed disparity map was stored in an external SRAM memory, also available in the development board. Many special debug utilities were developed because very a limited hardware debugging support was provided on Spartan development board.
All hardware implementation were made using Xilinx ISE IDE. This IDE provided by Xilinx Corp. allows programmable hardware development using VHDL and Verilog language, as well traditional graphic blocks schematic programming.
Although ISE provides simulation capabilities, an external VHDL simulator was used. For this purpose MentorGraphics ModelSim simulator was employed for verification of all created VHDL code.
Additional utilities were developed to convert the sample images to a compatible ModelSim file format.
E. Results
To verify the proposed algorithm, pairs of pictures from JISCT repository were used (dataset provided by research groups at JPL, INRIA, SRI, CMU and Teleos). This dataset features groups of images properly obtained for stereo vision processing.
The use of this dataset if specially interesting for future comparison of the obtained results with results of algorithms proposed by other researchers.
The source images were pre-processed, with a 4:1 reduction of size and use of an average anti-aliasing filter. This pre-processing stage was applied to adequate the pictures to the correct size and aspect ratio, as well to reduce the image high frequency components that would add excessive noise in the depth map.
The results shown in Table 1, Table 2 and Table 3 (column c) were artificially colored to evidence the depth of the objects in the scene. An arbitrary color map was used, where the nearest to the furthermost objects were shown from violet to red tonalities respectively.
Table 1. Results for the proposed algorithm: (a) and (b) are the source pair of stereo images, from JISCT dataset. (c) Shows the dense depth map for each scene. The results were colored from violet (nearest) to red (farthest) to enhance the images contrast.
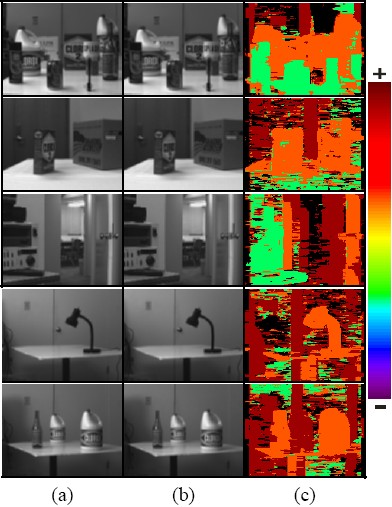
Table 2. Results for the proposed algorithm: (a) and (b) are the source pair of Tsukuba stereo images. (c) Shows the resulting dense depth map. The result was colored from violet (nearest) to red (farthest) to enhance the image contrast.

Table 3. Results for the proposed algorithm: (a) and (b) are the source pair of synthetic stereo images. (c) Shows the resulting dense depth map. The result was colored from violet (nearest) to red (farthest) to enhance the images contrast.

The pipelined structure, running at pixel-rate speed (576 kHz) could delivery the first disparity pixel after approximately 8.68ms. This allowed observing the disparity map of the scene without any noticeable delay or framing loss.
To process the pair of stereo images, a special routine uploaded them to the external SRAM of the stereo vision system, and after 33ms the disparity map was downloaded back to the computer, for analysis.
In the current research stage, fully integrated processing is being designed, adding pos-processing capabilities in the current pipeline structure. It is necessary for proper evaluation of the algorithm in real case scenario, such as robotic navigation and 3D scene mapping.
Also stereo pair from Tsukuba University was evaluated. Different ω and β coefficients were employed due to differences in cameras field of view. Parameter ω = 4 and β = 30 were used to process these images. Result is presented in Table 2.
A pair of synthetic images, available by computer vision group at Bonn University, was also analyzed.
These synthetic images, generated by a ray tracing software (MRTStereo - Modular Rendering Tools), feature ground truth disparity and occlusions. Result is presented in Table 3. Parameter ω = 5 and β = 7 were used to process these images.
IV. CONCLUSIONS
This paper has shown the feasibility of constructing high performance stereo vision system on programmable logic, while maintaining construction simplicity and low-cost.
Although there are some limitations, the system seems suitable for serving as an artificial depth reference for autonomous vehicle guidance. In special, the dense real-time depth maps provided by programmable hardware may continuously delivery high amounts of information to navigation and mapping software, lowering the usual computational burden involved in decoding and processing stereo camera images by conventional software methods.
Also, the proposed structure enables addition of post and pre-processed with low impact on processing time, allowing implementation of filters, algorithms for feature tracking, object recognition, among other possible proposals.
REFERENCES
1. Birchfield, S. and C. Tomasi, "Depth Discontinuities by Pixel-to-Pixel Stereo", Proc of the 1998 IEEE Int. Conf. on Computer Vision, Bombay, India 1073-1080 (1998a). [ Links ]
2. Birchfield, S. and C. Tomasi, "A Pixel Dissimilarity Measure That is Insensitive to Image Sampling", IEEE Trans. on Pattern Analysis and Machine Intelligence, 20, 401-406 (1998b). [ Links ]
3. Cox, I.J., S.L. Hingorani, S.B. Rao and B.M. Maggs, "A Maximum Likelihood Stereo Algorithm", Computer Vision and Image Understanding, 63, 542-567 (1996). [ Links ]
4. Darabiha, A., J. Rose and W.J. MacLean, "Video-Rate Stereo Depth Measurement on Programmable Hardware", Proc. of the 2003 IEEE Computer Society Conf. on Computer Vision and Pattern Recognition, 1, 203-210 (2003). [ Links ]
5. Grosso, E., G. Sandini and M. Tistarelli, "3D object reconstruction using stereo and motion", IEEE Trans. System, Man and Cybernetics, 19, 1465-1476 (1989). [ Links ]
6. Grosso, E. and M. Tistarelli, "Active/Dynamic Stereo Vision", IEEE Trans. On Pattern Analysis and Machine Intelligence, 17, 868-879 (1995). [ Links ]
7. Silva, L.C., A. Petraglia and M.R. Petraglia, "Stereo vision system for real time inspection and 3D reconstruction", Industrial Electronics, 2003. ISIE '03. 2003 IEEE Int. Symp., 1, 607-611 (2003). [ Links ]
8. Sunyoto, H., W. van der Mark and D.M. Gavrila, "A comparative study of fast dense stereo vision algorithms", IEEE Intelligent Vehicles Symposium, 319-324 (2004). [ Links ]
Received: April 14, 2006.
Accepted: September 8, 2006.
Recommended by Special Issue Editors Hilda Larrondo, Gustavo Sutter.














