Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.37 n.1 Bahía Blanca ene. 2007
Comparison of FPGA implementation of the mod M reduction
J-P. Deschamps1 and G. Sutter2
1 Escola Tècnica Superior d' Enginyeria, Universitat Rovira i Virgili, Tarragona, Spain,
jeanpierre.deschamps@urv.net; http://www.etse.urv.es
2 Escuela Politécnica Superior, Universidad Autónoma de Madrid, Spain,
gustavo.sutter@ii.uam.es; http://www.ii.uam.es.
Abstract — Several algorithms for computing x mod m are presented, among others the reduction mod Bk-a, the pre-computation of Bi.k mod m, a generalized version of the Barrett algorithm and a modified version of the same Barrett algorithm. The four mentioned algorithms, as well as the classical integer non-restoring division algorithm, have been synthesized and implemented within xc3s4000 components.
Keywords — Arithmetic in FPGA. Galois Field. Cryptography. Modular Operation.
I. INTRODUCTION
Arithmetic operations over the finite ring Zm = {0, 1, ..., m-1} are used as computation primitives for executing numerous cryptographic algorithms, especially those related with the use of public keys (asymmetric cryptography). Classical examples are ciphering / deciphering, authentication and digital signature protocols based on RSA-type or elliptic curve algorithms. One of the basic operations is the modulo m reduction. Combined with operations over the set Z of integers (sum, subtraction, product, and so on) it allows to perform the same operations over Zm. A straightforward solution consists of using an integer division algorithm. Nevertheless, more efficient algorithms have been proposed (Blake et al, 2002; Hankerson et al, 2004). In this paper several algorithms are described, namely the reduction mod Bk-a, the pre-computation of Bi.k mod m, a generalized version of the Barrett algorithm and a modified version of the same Barrett algorithm. The four mentioned algorithms, as well as the classical integer non-restoring division algorithm, have been synthesized and implemented within xc3s4000 components.
II. ALGORITHM
In this section the following problem is studied: given two naturals x and m, compute z = x mod m.
A. Integer division
A straightforward method consists of performing the integer division of x by m, that is,
x = q.m + z, z < m.
For that purpose, any division algorithm can be used, for example the non-restoring division algorithm (Deschamps et al, 2006).
Algorithm 1 - Non-restoring reduction

The core of the algorithm is an (n-k)-step iteration. If a ripple-carry k-bit adder-subtractor is used, the computation time is about
time(n,k) ≈ (n-k).k.TFA , (1)
where TFA is the delay of a full-adder.
B. Reduction mod Bk-a
Assume that Bk-1 ≤ m < Bk, where B is a natural number ≥ 2. Then m = Bk - a where 1 ≤ a ≤ Bk - Bk-1. Compute the following quotients qi and remainders ri:
| x = q0.Bk + r0, | (2) |
| q0.a = q1.Bk + r1, | |
| q1.a = q2.Bk + r2, | |
| ... | |
| qs-2.a = qs-1.Bk + rs-1. |
Multiply the second equation of (2) by (Bk/a), the third one by (Bk/a)2, ... , the last one by (Bk/a)s-1, and sum up the s equations; the result is
| x = r0 + r1.(Bk/a) + r2.(Bk/a)2 + ... | (3) |
| + rs-1.(Bk/a)s-1 + qs-1.Bk.(Bk/a)s-1. |
As a < Bk, that is, Bk/a > 1, there exists a minimum value of s such that
x < Bk.(Bk/a)s-1, (4)
and thus qs-1 = 0. Let s be the minimum value of s such that qs-1 = 0. Notice that if rs-1 = 0 then the last equation of (2), with qs-1 = 0, is qs-2.a = 0, that is, qs-2 = 0, so that s is not the minimum value of s such that qs-1 = 0. Thus
| x = r0 + r1.(Bk/a) + r2.(Bk/a)2 + ... + rs-1.(Bk/a)s-1, | (5) |
| with rs-1>0. |
By summing up the s equations of system (2), with qs-1 = 0, the following relation is obtained:
| x = q0.(Bk-a) + q1.(Bk-a) + ... + qs-2.(Bk-a) | (6) |
| + r0 + r1 + ... + rs-1. |
Define
r = r0 + r1 + ... + rs-1. (7)
According to (6) and (7),
x ≡ r mod m, with m = Bk-a. (8)
Comparing (5) with (7) it is obvious that if s > 1, that is, if x ≥ Bk, then r < x. If r is still greater than or equal to Bk, the same method can be used in order to get r' ≡ x mod m, with r' < r. After a finite number of iterations, a number r'' is obtained such that r'' ≡ x mod m and r'' < Bk, so that z = r'' - q.m where 0 ≤ q ≤ B-1. In particular, if B = 2 then z is either r'' or r''-m. To summarize, the mod m reduction algorithm, with m = Bk-a, is the following:
Algorithm 2 - mod m reduction algorithm, with m = Bk-a

If B is the base (or a power of the base) of the chosen numeration system, then the division by Bk and the mod Bk reduction are trivial operations. The only non-trivial operations are multiplication by a, sums (remainder accumulation) and subtractions (final reduction). The number of executions of the internal loop body can be estimated as follows: a sufficient condition for qs-1 being equal to 0 is (4), which is equivalent to s > (log x - log a) / (k.log B - log a). Thus s = ⌈(log x - log a) / (k.log B -log a)⌉. In particular, if x = Bn-1, that is, the greatest ndigit B-ary number, then
s = ⌈(n - logBa) / (k - logBa)⌉, (9)
and, assuming that logBa is much smaller than k and n,
s ≈ n/k. (10)
As regards the reduction rate of the algorithm, that is, the relation between an initial value x and the obtained value r after a first execution of the internal loop, notice that r is smaller than s.Bk, so that the number d(r) of B-ary digits of r satisfies the condition
d(r) ≤ k + ⌈logBs⌉, (11)
where s is approximately equal to (10). Thus d(rmax) ≈ logBn + k - logBk < logBn + k.
In order to define the size of the variable r = r0 + r1 + ... + rs-1, the following values are previously calculated (see (9) and (11)):
s = ⌈(n - log2a) / (k - log2a)⌉, t = ⌈log2s⌉,
so that r can be represented as a (k+t)-bit number.
The core of the algorithm is an (n/k)-step iteration. Each step includes the multiplication of an (n-k)-bit number q by a k-bit number a, and the sum of a (k+t)-bit number r and a k-bit number. The computation time of the multiplier depends on the particular value of a. Nevertheless, in order to get an estimation of the computation time, it will be assumed that a parallel multiplier is used. Its computation time is about ((n-k)+2.k-2).TFA ≈ (n+k).TFA (Deschamps et al, 2006). The step duration is approximately equal to (n+k).TFA + (k+t).TFA. If n+2.k >> t then the computation time is approximately equal to
time(n,k) ≈ (n/k).( n+2.k).TFA. (12)
C. Pre-computation of Bi.k mod m
Assume again that Bk-1 ≤ m < Bk, and that x is represented in base Bk, i.e.
x = xs-1.B(s-1).k + xs-2.B(s-2).k + ... + x1.Bk + x0, where xs-1>0. (13)
The following values must have been previously computed:
b0 = 1, b1 = Bk mod m, b2 = B2.k mod m, ... , bs-1 = B(s-1).k mod m.
Then x ≡ xs-1.bs-1 + xs-2.bs-2 + ... + x1.b1 + x0.b0 mod m, and the problem is reduced to the computation of r mod m where
r = xs-1.bs-1 + xs-2.bs-2 + ... + x1.b1 + x0.b0. (14)
Observe that bi = (Bi.k mod m) < m < Bk ≤ Bi.k , ∀ i > 0. Comparing (14) with (13), it is obvious that if s > 1, that is, if x ≥ Bk, then r < x. If r is still greater than or equal to Bk, the same method can be used in order to get r' ≡ x mod m with r' < r. After a finite number of iterations, a number r'' is obtained such that r'' ≡ x mod m and r'' < Bk, so that z = r'' - q.m where 0 ≤ q ≤ B-1. In particular, if B = 2 then z is either r'' or r''-m.
To summarize, the mod m reduction algorithm, with pre-computation of Bi.k mod m, is the following (it is assumed that the constants bi = Bi.k mod m have been previously calculated):
Algorithm 3 - mod m reduction, with pre-computation of Bi.k mod m

The mod Bk reduction and the integer division by Bk are trivial operations. The only non-trivial operations are products of base-Bk digits (vector_x(i)*b(i)) and sums, as well as the end of computation detection.
Let n be the number of B-ary digits of x. According to (13), xmax = Bs.k - 1, so that n = s.k and the number s of executions of the internal loop body is
s = n/k. (15)
As regards the reduction rate of the algorithm, notice that r is smaller than s.B2.k, so that the number d(r) of B-ary digits of r satisfies the condition d(r) ≤ 2.k + ⌈logBs⌉, where s is equal to (15). Thus
d(rmax) ≈ logBn + 2.k - logBk < logBn + 2.k. (16)
The core of the algorithm is an (n/k)-step iteration. Each of them includes the product of two k-bit numbers xi and bi, and the sum of two (log2n + 2.k)-bit numbers. The total computing time is approximately equal to
time(n,k) ≈ (n/k).(log2n + 5.k). (17)
D. Barrett reduction algorithms
A generalized version of the Barrett algorithm (Blake et al, 2002; Hankerson et al, 2004) is presented.
D.1 n-digit to (k+t)-digit reduction
Assume that m belongs to the range Bk-1 < m < Bk where B is the base (or a power of the base) of the chosen numeration system (if m is a power of B the computation of x mod m is trivial). The value of z = x mod m is the remainder of the integer division of x by m, that is, x = q.m + z, z < m. The Barrett algorithm starts with the computation of an approximation q' of q = ⌊x/m⌋ such that
q-a ≤ q' ≤ q. (18)
Compute
r' = x - q'.m. (19)
Taking into account that z = x - q.m, then, according to (18), z ≤ r' ≤ z + a.m. Let t be the minimum integer such that
Bt ≥ a+1. (20)
Then r' ≤ z + a.m < (a+1).m < Bk+t. Thus 0 ≤ z ≤ r'< Bk+t, so that
r' = r' mod Bk+t = (x -q'.m) mod Bk+t. (21)
Furthermore, according to (19)
r' mod m = x mod m = z. (22)
The following algorithm, including a function approximation which generates an approximation q' of ⌊x/m⌋-see relation (18) - , computes a (k+t)-digit number r equivalent to x mod m:
Algorithm 4 - n-digit to (k+t)-digit reduction

If a = 2 and B ≥ 3, then condition (20) is Bt ≥ 3 and is satisfied if t = 1. Thus x -q'.m can be computed mod Bk+1. This case corresponds to the classical Barrett algorithm.
D.2 A first approximation of q
Let x and m be expressed in base B:
| x = xn-1.Bn-1 + xn-2.Bn-2 + ... + x0.b0, |
| m = mk-1.Bk-1 + mk-2.Bk-2 + ... + m0.b0, where mk-1 > 0. |
The approximation q' of q = ⌊x/m⌋ is q' = ⌊⌊x/Bk-1⌋.⌊Bn/m⌋/ Bn-k+1⌋.
It can be demonstrated (Hankerson et al, 2004) that q ≤ q' + 2, that is a = 2.
According to (20) the value of t must be chosen in such a way that Bt ≥ 3. Thus
| if B = 2, then t = 2 (the computation is performed mod Bk+2), |
| if B > 2 (classical Barrett algorithm), then t = 1 (the computation is performed mod Bk+1). |
To summarize, the following algorithm computes z = x mod p. The constant
c = ⌊Bn/m⌋ (23)
must have been previously calculated.
Algorithm 5 - Generalized Barrett reduction

The division by Bk-1 or Bn-k+1 and the mod Bk+t reduction are trivial operations. The only non-trivial operations are the multiplication by m and the subtractions.
Comment In the classical Barrett algorithm (Blake et al, 2002; Hankerson et al, 2004), n is assumed to be equal to 2.k, so that
c = ⌊B2.k/m⌋, q' = ⌊⌊x/Bk-1⌋.⌊B2.k/m⌋/ Bk+1⌋.
Assuming (best case approximation) that the first value of r is already smaller than m, the computation time is the sum of the delays of an (n-k+1)-bit by (n-k+1)-bit multiplier (computation of w), a (k+t)-bit by k-bit multiplier (computation of q.m) and a (k+t+1)-bit subtractor. It is approximately equal to ((3.(n-k+1)-2) + (k+t+2.k-2) + (k+t+1)).TFA. If 2.t << 3.n+k, then
time(n,k) ≈ (3.n+k).TFA. (24)
A drawback of the Barrett algorithm is the high cost of the multipliers. The cost of an n-bit by m-bit multiplier is proportional to n.m (Deschamps et al, 2006). Thus, the total cost of both multipliers is proportional to (nk+1)2 + (k+t).k ≈ (n-k)2 + k2 whose minimum value (for k smaller than n) is n2/2 (when k = n/2).
D.3 A second approximation of q
In order to reduce the computation complexity (basically the computation of w), a worse approximation of q can be computed. First observe that c = ⌊Bn/m⌋ is an at most (n-k+1)-digit number. Thus
w = y.c = c0.b0.y + c1.b1.y + ...+ cn-k.Bn-k .y,
q' = ⌊y.c / Bn-k+1⌋ = ⌊c0.B-n+k-1.y + c1.B-n+k .y + ...
+ cn-k.B-1.y⌋. (25)
Define q'' = c0.⌊B-n+k-1.y⌋+ c1.⌊B-n+k .y⌋+ ...+ cn-k.⌊B-1.y⌋, that is
q'' = c0.v0 + c1.v1 + ... + cn-k.vn-k,
with vi = ⌊y/Bn-k-i+1⌋, ∀i = 0, 1, ... , n-k. (26)
Obviously q'' ≤ q'. Furthermore q' ≤ q''+ c0 + c1 + ...+ cn-m = q'' + weight(c), where weight(c) is the sum of all digits of c. Thus q' - weight(c) ≤ q'' ≤ q' and q - 2 - weight(c) ≤ q'' ≤ q, that is, q'' is an approximation (18) of q such that a = 2 + weight(c).
Algorithm 6 â Modified Barrett reduction

The division by Bk-1 or Bn-k-i+1 and the mod Bk+t reduction are trivial operations. The only non-trivial operations are multiplications by B-ary digits ci (a trivial operation if B=2), multiplication by m, additions and subtractions. The computation is divided into two parts. First, an (n-k)-step iteration computes q. The corresponding time is approximately (n-k).(k+t).TFA ≈ (nk).k.TFA. Assuming again (best case approximation) that the first value of r is smaller than m, the second part consists of a (k+t)-bit by k-bit product (q.m) and a (k+t)bit subtraction, that is, a delay equal to ((3.k+t-2) + (k+t)).TFA ≈ 4.k.TFA. Thus, the total time is about
time(n,k) ≈ (n-k+4).k.TFA ≈ (n-k).k.TFA. (27)
E. Summary
The main results are summarized in table 1. The approximate computation time, expressed in full-adder delays, is given for every reduction method. In particular, the values obtained when n = 2.k are computed: they correspond to the case where x is the result of multiplying two elements of Zm, that is, two k-bit numbers.
Table 1. Computation time, expressed in full-adder delays, for reducing an n-bit number modulo a k-bit number

As long as the computation time is considered, and assuming that the approximations are reasonably good, the Barrett algorithm is the best choice. Nevertheless, as quoted above, its cost is O(n2) and could be prohibitively high for great values of n (see next section) .
III. FPGA IMPLEMENTATIONS
Reduction circuits, with n = 2.k = 16, 64, 256 and 1024, have been synthesized using ISE6.3i (Xilinx, 2006). The results for an xc3s4000-5 device are given in tables 2 to 6. The cost is expressed in number of slices. Apart from the logic slices, both Barrett algorithms need a lot of 18by-18-bit multipliers. The xc3s4000-5 device contains 96 such dividers, an insufficient number for implementing Barrett algorithms for great values of n. This fact is indicated by the v symbol within the cost column. Reduction circuits for n = 64 and m = 239, so that k = 8, have also been synthesized (table 7).
Table 2. Non-restoring division: cost and computation time (n = 2.k)
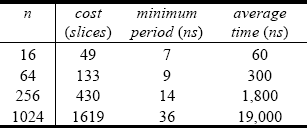
Table 3. Reduction mod 2k-a: cost and computation time (n = 2.k)
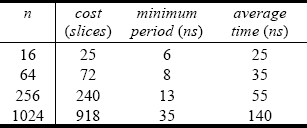
Table 4. Pre-computation of 2i.k mod m: cost and computation time (n = 2.k)
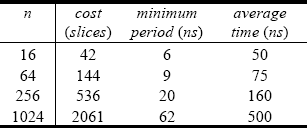
Table 5. Barrett algorithm: cost and computation time (n = 2.k)
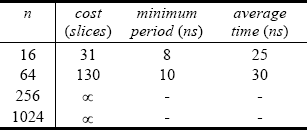
Table 6. Modified Barrett algorithm: cost and computation
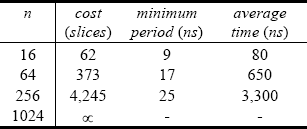
Table 7. Cost and computation time (n = 64 and m = 239)

IV. COMMENTS AND CONCLUSIONS
According to both the theoretical analysis (table 1) and the practical synthesis results (tables 2 to 7), the fastest circuits are obtained with the Barrett algorithm. Nevertheless, the corresponding costs are excessive for great values of n. The second best solution, as regards the computation time, is the reduction mod 2k-a. Actually, these conclusions are valid as long as generic reduction circuits are considered. For specific values of n and m, the pre-computation option could be an interesting alternative (chapter 8 of Deschamps et al, 2006). For small values of n, the best option is a block of ROM storing the 2n pre-computed values of x mod m. In the case where the reduction is part of an algorithm including a lot of multiplications, for example an exponentiation algorithm, an alternative solution is the Montgomery product (Montgomery, 1985). It has not been studied in this paper dedicated to reduction circuits, but is one of the main topics of another (not yet published) work on finite ring and field operations.
REFERENCES
1. Blake, I.V., G. Seroussi and N. Smart, Elliptic Curves in Cryptography. Cambridge University Press (2002). [ Links ]
2. Hankerson, D., A.J. Menezes and S. Vanstone, Guide to Elliptic Curve Cryptography, Springer (2004). [ Links ]
3. Deschamps, J.-P., G.A. Bioul, and G.D. Sutter, Synthesis of Arithmetic Circuits, Wiley (2006). [ Links ]
4. Montgomery, P., "Modular Multiplication without Trial Division", Mathematics of Computation, 44, 519-521 (1985). [ Links ]
5. Xilinx Inc, http://www.xilinx.com (2006). [ Links ]
Received: April 14, 2006.
Accepted: September 8, 2006.
Recommended by Special Issue Editors Hilda Larrondo, Gustavo Sutter.














