A fuzzy dynamic programming approach for evaluation of expansion distribution cost in uncertainty environments

G. A. Schweickardt¹ and V. Miranda²

¹ Instituto de Economía Energética - Fundación Bariloche - Av. Bustillo km 9,500 - Centro Atómico Bariloche - Pabellón 7, Argentina
gustavoschweickardt@ciudad.com.ar
² INESC Porto - Instituto de Engenharia de Sistemas e Computadores do Porto and FEUP - Faculdade de Engenharia da Universidade do Porto. Dr. Roberto Frias, 378 - 4200-465, Porto, Portugal
vmiranda@inescporto.pt

Abstract — This paper presents a new Fuzzy Dynamic Programming model that calculates the optimum solution of problems with uncertainties in data defined by fuzzy sets. The result includes the determination of an Intrinsic Risk Threshold of the solution. Extrinsic Risk Thresholds may also be set by a Decision Maker, in order to obtain more robust solutions. The technique is applied to the calculation of Distribution System expansion costs to serve the objectives of a Regulatory Authority (Regulator) in fixing levels of efficiency, targets and penalties to a regulated market.

Keywords — Distribution Planning. Fuzzy Dynamic Programming. Risk Analysis. Risk Threshold. Fuzzy Regret.

I. INTRODUCTION

Distribution expansion planning is no longer an activity that only interests utilities. In a market environment, where several actors may participate or contribute to the evolution of distribution systems, regulators have the need to evaluate the impacts and costs of this evolution, too.

This is especially relevant when the regulator wishes to define a theoretical case for distribution expansion costs, in order to be able to compare the actual performance of an utility with such reference - this may allow the establishment of efficiency measures that may have consequences on the rewards allowed to the distribution utilities, on the assessment of added costs induced by external factors or in fixing penalties.

However, the definition of a theoretically optimal expansion cost is not easy, not only because of the complexity of the problem but also due to the level of uncertainties present in data and in forecasts. Therefore, one must develop models in which these uncertainties are recognized and treated as such.

But the incorporation of uncertainties in a system expansion model in which decisions are sequentially made, cannot be done without considering risks associated with such decisions.

Besides, many of the uncertainties are not of probabilistic or stochastic nature and should not be represented as such - in this case, representing uncertainties by Fuzzy Sets is an alternative.

In this paper, a solution to a mid-term distribution expansion planning problem is proposed, from the perspective of a Regulator. Along several stages in time, one searches for the set of decisions (associated with investment costs - new lines, new substations - and operation costs - namely power losses) that "optimize" the global cost of system development. However, because of uncertainties (in power demand, in equipment costs) this goal cannot be achieved: depending on the instantiated values for data with uncertainty, the optimal decisions may vary.

In the work reported in this paper, the development of a distribution system is simulated, according to a Dynamic Programming principle. This simulation intends to retain the set of decisions that may be optimal in distinct scenarios, in order to seek the sequence of decisions that may display, as much as possible, a degree of immunity to uncertainties. These sets of decisions may be seen as a fuzzy trajectory through system state space. By establishing thresholds, delimiting admissible from inadmissible risk levels, one is able to control the size of the corresponding optimizing fuzzy trajectory.

This is a Risk Analysis paradigm approach - decisions are selected in order to minimize the possible regret felt, in case the future demonstrates that the decision made was not optimal. In the following sections, the model will be described and its usefulness illustrated.

II. METHODS

A. Discussing the Fuzzy Dynamic Programming

There is an algorithm in the class of Dynamic Programming (Bellman and Dreyfus, 1962), called Fuzzy Dynamic Programming, which enables the calculation of an optimum of certain problems that include uncertainties, modeled as fuzzy sets, in constraints and objective function - following the Optimality Principle of Bellman-Zadeh (1970). This principle leads to the calculation of a maximizing decision (maximizing a membership degree) over the intersection of objective and constraints.

However, the result offered by this approach is still a simple trajectory over a deterministic or crisp space of system states. Therefore, there is not an explicit account of risk in the decision making process, and a Decision Maker can only implicitly consider it by defining an order of importance or hierarchy in the problem criteria (Sakawa, 1993; Saaty, 1977; Shu and Kuo, 1992; Yager, 1977). In this sense, the notion of risk is more dependent on the relative aversion of the planner to criteria than on the Structure of Uncertainties of the problem.

In the following paragraphs, an alternative Dynamic Programming approach is presented, in which the uncertainties, under the form of fuzzy numbers, condition the search for optimizing strategies in a space of fuzzy states. In this formulation there is not a clear single optimizing trajectory in the space of system states but instead a fuzzy set of trajectories (a set of trajectories, each with a membership value). This result is extremely important if one wishes to deal with uncertainty and risk. The concept of risk only makes sense if one is able to consider different scenarios and evaluate the consequences of decisions in each scenario. The scenarios are generated or result from the recognition of uncertainties. By keeping trace of the optimizing trajectory for each scenario, one retains the ability to evaluate regrets and therefore to keep track of the robustness of decisions.

Because the space state may be very large, its dimension is reduced with the help of the concept of Fuzzy Regret (Miranda, 1998) regulating the choices among alternatives.

B. Ranking the Fuzzy Numbers

General Comments

One necessary step in every optimization technique is to compare alternatives. If their values are expressed as fuzzy numbers, then the problem becomes more complicated, because there is not a strict relation of order definable in the set of fuzzy numbers but only a relation of partial order. However, for practical purposes, the application of a sequence of criteria may help in ranking fuzzy alternatives.

Among the proposed methods, the Removal criterion (Kaufmann and Gupta, 1985) and the Total Distance Criterion or Generalized Hurwicz Criterion (GHC) (Saade, 1996) may be mentioned. One must also mention the possibility of ranking fuzzy numbers using a defuzzification approach such as the Center of Mass, often used in Control but not usually in Decision Making.

Also a definition of a fuzzy maximum C of two fuzzy numbers A and B, such as proposed by Kaufmann and Gupta (1985), based on the membership functions µ of A, B and C

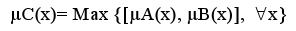
(1)

is not useful in decision making when comparing alternatives: in this case, one is searching for reasons to prefer A over B and not trying to obtain any kind of "fusion" between the alternatives.

Risk and α-cut of Fuzzy Numbers

A fuzzy number, represented by a membership function, can be seen as a set of nested intervals, each associated with a membership level α. This parameter, in the context of decision making, is a measure of the risk of accepting an α-cut as representative of the concept described by the fuzzy number. This risk level is defined in the interval [0,1]. See Fig. 1, below.

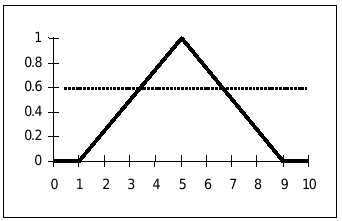
Figure 1 - Fuzzy number "more or less 5" and an α-cut at level 0.5

In Fig. 1 a possible fuzzy representation of "more or less 5" is illustrated; one may see that level α = 0.5 corresponds to the interval [3,7], while for a higher level of risk such as 0.7 the interval [4,6] must be adopted as a surrogate of "more or less 5". Of course, the highest risk corresponds to level 1, taking the "exact" or "crisp" number 5 as a representation of "more or less 5".

Intrinsic Risk Threshold and Partial Comparison of Fuzzy Numbers

Now observe Fig. 2. Admit that A and B represent the values associated to two alternative investment decisions.

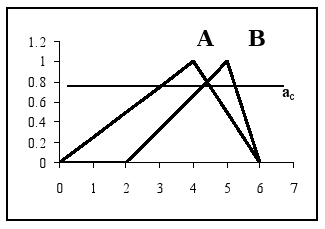
Figure 2 - Definition of the Risk Level a_c, above which one has B > A regardless of the expression of uncertainties

Above level a_c, it is guaranteed that, no matter what the crisp instantiation of A and B is, the value of B will always be greater than A.

This "exposure level" defines the maximum amplitude of uncertainty in both A and B that one may accept while being certain that one alternative will always be preferred over the other.

The lower a_c, is the more confident one may be that selecting B over A will not be a regrettable decision; of course, if a_c=0 one is absolutely sure that, no matter what the crisp outcome values of A and B may be, after the uncertainties are solved, the ordering of alternatives is maintained.

Level a_c is a risk level. In this work, it will be indicated as the Intrinsic Risk Threshold. Of course, there is no risk if a_c=0 and the risk is maximum if a_c=1 (when there is no confidence level for which selecting B over A is a safe decision). Notice that the definition of the intrinsic risk threshold depends on the establishment of a decision gradient in the attribute space where the fuzzy values of alternatives are represented: when comparing A with B, the risk threshold is different whether one is trying to decide if B is preferable over A or A to B.

Therefore, in the presence of a decision making process with several alternatives with uncertainty, it is important not only to select a preferred alternative but also to identify the intrinsic risk level of such selection - this will define the degree of exposure of the decision to adverse futures. This process will be indicated as Partial Comparison of Fuzzy Numbers (Alternatives).

Fuzzy Regret

Another important decision factor when comparing alternatives is the concept of fuzzy regret.

In risk analysis, regret is a measure of how sorry a Decision Maker is likely to feel for having selected one alternative, in a context of uncertainty, and then later realizing that, if a Decision Maker had known the future with certainty, another alternative would have been better (Miranda and Proença, 1998).

Admit two alternatives valued by two overlapping fuzzy numbers A and B such as in Fig. 3. Admit also that the uncertainties associated to each outcome are independent.

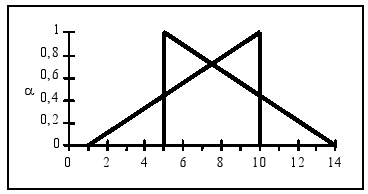
Figure 3 - Two triangular fuzzy numbers A(1,10,10) and B(5,5,14)

Checking Fig. 3, it is possible to observe that at higher α levels, B is always less than A but at lower levels B may exceed A.

Without loss of generality, let's assume a context of minimization. A fuzzy number Reg(A|B) will be define as the possible regret felt by a Decision Maker when he chooses A but then B occurs; using the segment of confidence notation (Kaufmann and Gupta, 1985):

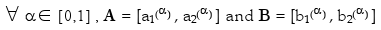
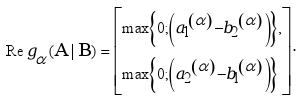
	(2)

Of course, if one chooses A and A results better than B, no regret will be felt - that's why the above expression does not allow for negative regrets.

In Fig. 4, the two fuzzy numbers Reg(A|B) and Reg(B|A) are represented. In a decision context, the smaller the potential regret, the better. One may now rank the two fuzzy regrets using any defuzzification technique. In the case of Fig. 4, a criterion such as the Center of Mass places Reg(B|A) < Reg(A|B) - therefore, decision B would be preferable over decision A, in this pairwise comparison.

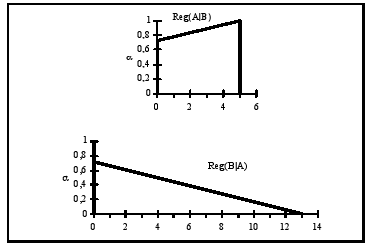
Figure 4 - Fuzzy Regrets, referring to Figure 3. Top - regret for choosing A instead of B; bottom - regret for choosing B instead of A

The relevant point to be kept is that decisions about fuzzy valued solutions must be weighted in pairwise comparisons, while solution fuzzy values may be ranked based on individual defuzzified values.

C. Fuzzy Dynamic Programming Model

General Model

The classical Dynamic Programming model assumes deterministic conditions in the decision process. The Bellman Optimality Principle states that

(3)

where:

Opt = Optimum (min or max, according to the problem)
f^* = Optimum value of objective function f, at a given state and Stage
(j, K)= State j corresponding to Stage K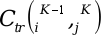
= Variation of function f between States (i, K-1) and (j, K) = Transition cost between those states in their Stages. One could apply the Extension Principle (Kaufmann and Gupta, 1985) to generate a fuzzy version of the Optimality Principle, where the values of variables are fuzzy and therefore one must use extended operations to do the calculations. However, the problem in making comparisons between alternatives must be dealt with, in order to decide, at each Stage, what the Optimal partial decision is.

According to the principles of partial comparison defined in Section B, each comparison between fuzzy objective function values and the consequent decision of preferring one over another implies accepting a certain intrinsic risk threshold (above which the decision is not questioned). As a large number of comparisons will exist during the optimization process, one will collect an equal number of intrinsic risk thresholds.

Operational Definition of Intrinsic Risk Threshold

What is the Intrinsic Risk Threshold for the problem solution, given the possible trajectories along system Stages? The answer is to take the maximum:

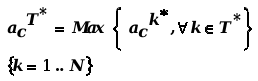
(4)

with:

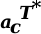- the Intrinsic Risk Threshold of the Optimum Trajectory T* along Stages
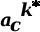- the Intrinsic Risk Level associated to each State k included in T*
N - the number of Stages of the problem.

This means that the Optimizing trajectory (which leads to the Optimal Solution) is only risk-safe or Robust if the uncertainties are represented by narrower intervals than the ones defined by the α-cut at a_c^T*.

D. Fuzzy Optimization Model for Distribution Expansion Cost

The development of a distribution system is a multi-stage multi-criteria problem in a context of uncertainty. The evaluation of the possible cost for a preferred development strategy may be done using the concepts of Fuzzy Dynamic Programming described in the previous sections.

Before presenting a practical application, some relevant aspects of the model are discussed:

Multiple attributes and Aggregated Objective Cost

There is a set of criteria that may be represented by an economic value or an equivalent, which allows their consolidation into a single value. The most important are:

• I: Investment;
• Perd: Losses;
• QS - Quality of Supply, usually evaluated by ENS - Energy not Supplied;
• EI - Environmental Impact (for a distribution system, it will be measured through an index of visual impact of overhead lines and transformers).

The economic evaluation of each attribute requires the definition of Opportunity Costs. Furthermore, three main types of agents acting in the market environment can be identified; two of them have conflicting rationales (utilities and consumers) and a third one acts on behalf of a collective welfare (the Regulator).

This last agent has the responsibility to identify what, in a market equilibrium theoretical context, would be a set of opportunity costs such as the value of Power Quality or Environmental Quality. These lead to setting Objectives for quality levels, that must be reached through the application of Incentives and Penalties to the other agents. These Penalties will therefore constitute the costs of the (no) Quality of Supply and Environmental Impact that an utility must take into account in a Distribution Expansion Planning activity.

If all these attributes are valued as costs, it is possible to aggregate them into a single attribute and, in this respect, deal with the planning problem as a single objective model instead of a multiple criteria model.

Financial Uncertainties

Many of the financial uncertainties in planning are related to the value of the interest rate or opportunity cost used in evaluating equivalent capital costs. The CAPM (Capital Asset Pricing Method) approach (Bodie et al., 1999) evaluates the return rate to be applied as

t _CAPM = [ t _f + ß _d ( t _m - t _f ) ] (5)

with:

t _CAPM : return rate
t _f : risk free asset return rate
ß_d : Systematic risk in the Power Industry
t_{m :} return of a diversified portfolio with ( t _m - t _f ) as the market risk premium.

Numbers and therefore, a fuzzy t_CAPM can be defined, then, the equivalent capital costs will be fuzzy.

Demand Forecast Uncertainties

Uncertainties in demand forecast must be taken into account. There are a number of methods to consider uncertainties in demand predictions, from projections based on econometric models to more complex models.

From these predictions one may build Possibility Distributions associated to the demand forecast.

Power Flow simulation

Given fuzzy loads, one must adopt fuzzy models to verify the loading of equipment in each investment variant. One of such models is the Fuzzy Load Flow (Miranda et al., 1990).

Reliability

There are also models to deal with reliability in a fuzzy environment. The results may be fuzzy ENS (Energy Not Supplied) and fuzzy reliability costs (Miranda, 1998).

Fuzzy Objective Function

The objective function to be minimized will be the Fuzzy Net Present Value (FNPV) of all aggregated costs during the study period

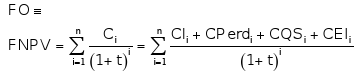
(6)

with each Cx_i being the cost associated to each attribute, i the Stage index and n the number of Stages in the planning period.

In particular, each Fuzzy Capital Cost for each alternative v (of using distinct equipment solutions) is given by

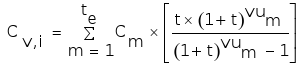
(7)

with:

C_v,i: fuzzy annualized investment associated with alternative v in Stage i,
C_m: fuzzy annualized cost associated with equipment m,
t_e: total number of pieces of equipment in alternative v,
vu_m: useful life of the equipment m in such alternative,

(8)

is the Fuzzy Capital Recovery Factor,
t: fuzzy return rate.

Constraints

An alternative is based on a set of resources satisfying all technical conditions imposed at each Planning Stage. Not all combinations of pieces of equipment or resources are possible. A combination of alternatives is only possible if

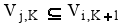
(9)

where V_j,K denotes the set of equipment pieces forming alternative j up to Stage K. This condition gives coherence to a trajectory through states along the Planning Stages.

Extrinsic Risk Threshold

The Intrinsic Risk Threshold, defined above, results from all the uncertainties considered in the model. However, it may happen that this threshold is unacceptable to the Decision Maker, because it is too high, leading to intervals (of stability of the solution given the uncertainty in data) that are too narrow.

Instead, the Decision Maker may wish to impose an Extrinsic Risk Threshold as a constraint - meaning that he does not wish to select options that reduce the capacity to absorb uncertainty. He is therefore searching for robust strategies, or stable decisions within a certain interval of uncertainty of data. This means that the decision process may discard alternatives that could perhaps have a smaller cost, but that become sub-optimal very easily, depending on the actual outcome values of parameters affected by uncertainty in data. This, in fact, contributes to reduce the state space, eliminating alternatives leading to a high risk. This elimination can be made applying the concept of fuzzy regret explained above: by making pair-wise comparisons of alternatives, the Decision Maker may discard from further examination an alternative that shows a higher potential regret.

This can also be seen as a hedging attitude: the Decision Maker accepts a higher possible cost but becomes surer of having decided for a more stable strategy, i.e., with an evaluation of the interval of uncertainty that will less likely lead to unpleasant surprises.

Trade-off calculation

Setting an Extrinsic Risk Threshold defines a level of risk taken by the Decision Maker (that the solution he chooses may become unacceptable in a set of adverse scenarios included in the intervals of uncertainty contained above such threshold).

One may therefore develop a trade-off calculation, identifying the relation between (extrinsic) risk threshold and selected system expansion strategy. Typically, the global cost will increase if one aims at having a solution trajectory that is insensitive to larger uncertainties.

Independence of uncertainties

When doing the partial comparison of two fuzzy numbers, one must identify uncertainty sources that are common to both numbers so that a real risk threshold is identified, instead of an apparent threshold.

If uncertainties are wrongly mistaken as fully independent from a common source, the resulting uncertainty is much larger than it should be. Only the uncorrelated uncertainties must be counted for in determining the actual risk threshold level.

Summary

The model developed to evaluate the cost of an ideal expansion strategy for a distribution system may be summarized as follows:

(10)

subject to

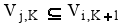(Coherency of Choices)

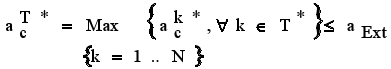
(Extrinsic Risk Threshold constraint)

This problem is solved by applying recursively the Bellman's Optimality Principle, extended to the fuzzy domain:

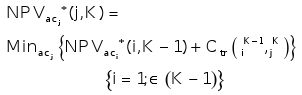
(11)

where NPV stands for Net Present Value and Min_ac means that the decisions are made following the Partial Comparison Principle, which is associated with a Risk Threshold a_c, as explained above.

Proposed Model of Fuzzy Optimization and the State of Art in Planning Distributions Systems

In this paper, a solution of mid-term distribution expansion planning problem, from the perspective of a Regulator, is proposed. The basis for this model, is the Bellman's Optimality Principle, under its formulation in the Dynamic Programming Optimization method. It's an extensively used tool in dynamic planning systems. In the State of Art (Distribution System's Planning), it has been applied in pseudo-dynamic (long-mid term) (Ramírez-Rosado and Gönen, 1991) and dynamic (mid-short term) (Youssef and Hackam, 1988; Partanen, 1990) planning. In general, this plannig has two stages: 1) long-term and 2) mid-(short)term. In the former, allocation of substations and feeders are defined for each sub-stage (grouping some years) as alternatives of equipment. In the second, mid-term, these alternatives, with more details in investments, to make up the states of the Search Space to application of classic Dynamic Programming. Here, in the mid-term, is where the Bellman's Principle is used to solve both models: classical and proposed.

But from the Regulator's point of view, there is a deficiency in economic assessment of objectives and constraints, that distribution system expansion problems exhibit (except in investment cost of equipment). However, in some regulations (Argentinean, for example), penalty factors are imposed to the utilities, over a basis of some limits in quality of service and, less frequently, environmental quality. These factors are not defined in an objective way. Therefore, they have uncertainties whose treatment in the regulation process is not established clearly. Only a level cost for each penalty is known, but it does not participate as element of expansion model, rather as component of control distribution system exploitation, once its planning is available.

The proposed model assumes that costs of penalty factors are opportunity costs, in economical sense. Additionally, the lack of clarity in its definition (uncertainties), is modeled, as an alternative, via fuzzy sets. In this way, an approximation of an aggregate of opportunity costs, one for each objective or constraints in the model (namely attributes), has a possible formulation. This aggregate will be a fuzzy cost to be minimized in the mid-term horizon of planning.

Therefore, the planner-Regulator has a new formulation in planning distribution systems, where all attributes, as "fitness" measures (opportunity cost) of system, are integrated. Then, the search for fuzzy minimum expansion and operation cost follows, defined, finally, by means of a segment of confidence (values in alpha-cut of fuzzy set cost). The Search Space of the problem is bounded by a constraint of coherence of choice in equipment variants, Eq. (9), and the application of Bellman's Optimality Principle, extended to fuzzy domain, is then valid and appropriate, under the rules imposed for the Extension Principle in fuzzy sets and numbers (Kaufmann and Gupta, 1985).

E. Case Study

Comments

The methodology described above was applied to the case of the distribution system exploited by the utility of the region of Bariloche, in the Argentinean Patagonia. The period under analysis was the sequence of years 1998-2002, corresponding to a 5-year Tariff Control period denoted in Argentina as a Quinquenio. The Distribution Network of Bariloche covers an area of 350 km² around the lake Nahuel Huapi (500 km²). It is supplied at 33 kV and it has three 33/13.2 kV substations. The 13.2 kV lines feed about 400 LV substations of an average installed capacity of 150 kVA. The local weather conditions are hard, characteristic of a mountain region. The quality of supply suffers from these conditions. This is a winter tourist destination (which imposes some strong environmental constraints). This is a fast developing area, where new consumers dominate over the growth of existing consumption, which explains why the expansion costs become relevant in the planning of the network.

All fuzzy data (costs, demand forecasts...) as well as the results from operations with fuzzy numbers were represented by trapezoidal membership functions. It is a reasonable approximation that is adopted in many circumstances. The reliability calculations were performed based on a model that is consistent with the regulatory environment in Argentina, which imposes penalties to all non supplied Energy.

Simulation

The simulation corresponded to a period of five years which was divided in five stages. A number of possible network expansion reinforcements and development alternatives were considered, and the following were retained, complying with a constraint for possible combination of alternatives: Stage 1: 5 alternatives; Stage 2: 4 alternatives; Stage 3: 4 alternatives; Stage 4: 3 alternatives; stage 5: 1 final stage.

The annualities corresponding to fuzzy costs are expressed in k$/year. One cannot fully describe in the paper all the details of the example, but some graphs illustrate the results obtained. Figure 5, for example, illustrates the decision process at Stage 2 departing from the partial optimal found at stage 1. One of the variants is clearly better and it represents an Intrinsic Risk Threshold of 0.6723, compared with the next best (as marked in the figure). Figure 6 illustrates the result at the end of the process.

Figure 5 - Fuzzy partial optimum in the transition of Stage 1 to Stage 2

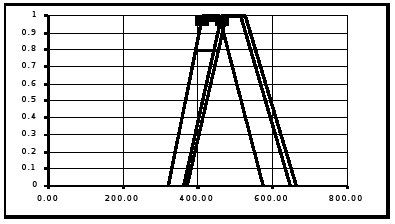
Figure 6 - Fuzzy partial optimum, in the transition of Stage 4 to Stage 5. The apparent accumulated Intrinsic Risk Threshold is now 0.9746

A back-tracking procedure has been developed to identify dependencies in uncertainties in a trajectory along the several stages, so that a Real Risk level could be calculated. This has enabled the identification of a Real Intrinsic Risk Threshold for the optimal solution. The Apparent Risk, is a consequence of dependence on the uncertainties inherent to all the fuzzy numbers (cost) that are component of aggregate fuzzy cost, for each state, in the fuzzy minimum trajectory building.

The following table summarizes such calculations:

The successive application of the concept of Fuzzy Regret, reducing the state space, leads to the elimination of states that could have been better in some futures. To be safe in his evaluation of the interval of uncertainty, the Decision Maker has renounced to be pleasantly surprised in the future, in some scenarios. This has been observed through the building of a graph denoting the increase in the "accumulated value of discarded surprises" with the decrease of the Risk Threshold resulting from the application of the Minimum Fuzzy regret procedure to reduce the state space.

Let 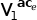y be two alternatives defining an Intrinsic Risk Threshold ac_e in the Optimal Fuzzy Path at a given state e. Let 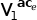be preferred over , when applying the Minimum Fuzzy Regret principle to reduce such threshold. Then, a Surprise Index was calculated as:

(12)

with E being the number of eliminated states. Figure 7 shows the calculated values of S with successive state elimination, using two defuzzification criteria (Removal and GHC). The key Cpso means the defuzzification criteria employed - Collapse of Possibility Distribution.

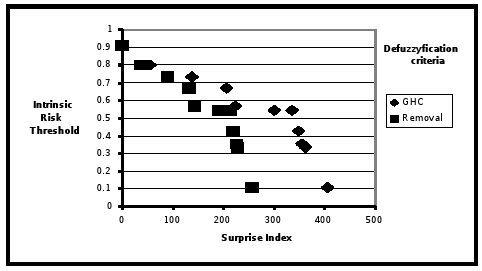
Figure 7 - Variation of the value of discarded states with the decreasing choice of Risk Threshold

Then, Sis a measure of over-cost respect the fuzzy minimum, that appears when the planner-regulator "feel" the Intrinsic Risk Threshold very high. Formally, this situation implies that Extrinsic Risk Threshold constraint was violated. If this event occurs, the proposal model proceed to eliminate the state of minimum fuzzy regret in the fuzzy space, Cpso, by means of steps describe above. The Real Risk decreases, confidence increases, but the minimum fuzzy cost increases too.

Some relevant results are commented as follows:

1. The minimum Fuzzy Net Present Value is calculated as lying inside the interval [404,74 ; 468,44] k$/year, determining an Intrinsic Risk Threshold of a_c^T=0.9134, when direct comparisons are made between fuzzy numbers.
2. However, if one adopts the minimum fuzzy regret evaluation when deciding using eq. (12), one reaches a risk threshold of a_c^T=0.7992 defining a minimum FNPV within [394,42 ; 481,87] k$/year.

III. CONCLUSIONS

This paper deals with the problem of finding the cost of an optimal expansion strategy for a distribution system over a given period of time.

The Regulator must take into account, in his evaluation, a number of uncertainties both in costs and in demand forecasts. Therefore, the Regulator must be able to calculate a credible interval for the costs associated with an expansion strategy and he must also have an indication of the risk of accepting this interval or of regretting such decision.

The paper offers the following contributions:

• A Fuzzy Dynamic Programming Optimization model that determines an optimum expansion strategy while keeping track of the uncertainties in data and its reflection on results.
• A model that calculates the Intrinsic Risk Threshold of the optimum strategy, i.e., that defines the size of the uncertainty interval for which one is sure that, no matter what the instantiation of uncertainties may be, the solution will remain as the selected one
• A model that may accept an Extrinsic Risk Threshold as a constraint, so that the user may opt for a more robust set of decisions; this may lead to a sub-optimal evaluation of the cost, but the Decision Maker may be more confident of being immune to a wider range of uncertainties (it is a way of obtaining some hedging against adverse futures).
• A model that may give the Decision Maker an indication about a Trade-Off between an over-evaluation of the expansion costs and an increase in the robustness of the decisions.

REFERENCES
1. Bellman, R., and E. Dreyfus, Applied Dynamic Programming, Princeton University Press (1962).         [ Links ]
2. Bellman, R., and L. Zadeh, "Decision-Making in a Fuzzy Environment", Management Science 17, B-141-164 (1970).         [ Links ]
3. Bodie, Z., A. Kane and A. Marcus, Investments, Irwin/McGraw-Hill Series in Finance, Insurance and Real Estate, 4th Edition (1999).         [ Links ]
4. Kaufmann, A., and M. Gupta, Introduction to Fuzzy Arithmetic. Theory and Applications, Van Nostrand Reinhold Electrical/Computer Science and Engineering Series (1985).         [ Links ]
5. Miranda, V., "A Fuzzy Perspective of Power System Reliability", Electric Power Applications of Fuzzy Systems", ed. M.el-Hawari, IEEE Press (1998).         [ Links ]
6. Miranda, V., M. Matos and J.T. Saraiva, "Fuzzy Load Flow - New Algorithms Incorporating Uncertain Generation and Load Representation", Proc. of the 10^th PSCC, Graz, Austria, ed. Butterworths (1990).         [ Links ]
7. Miranda, V. and L. Proença, "Why Risk Analysis Outper-forms Probabilistic Choice as Effective Decision Support Paradigm for Power System Planning", IEEE Transactions on Power Systems, 13, 643-648 (1998).         [ Links ]
8. Partanen, J., "A Modified Dynamic Programming Algorithm for Sizing Locating and Timing of Feeder Reinforcements", IEEE Trans. on Power Delivery, PWRD-5, 277-283 (1990).         [ Links ]
9. Ramírez-Rosado, I.J., and T. Gönen, "Pseudodynamic Planning for Expansion of Power Distribution Systems", IEEE Trans. on Power Systems, PWRS-6, 245-254 (1991).         [ Links ]
10. Saade, J., "A Unifying Approach to Defuzzification and Comparison of the Outputs of Fuzzy Controllers", IEEE Transactions on Fuzzy Systems, 4, 227-237 (1996).         [ Links ]
11. Saaty, T.L., "A Scaling Method for Priorities in Hierarchical Structures", J. Math. Psychology, 15, 234-281 (1977).         [ Links ]
12. Sakawa, M., Fuzzy Sets and Interactive Multiobjective Optimization, Plenum Publishing Corporation, New York (1993).         [ Links ]
13. Shu, Y.Y., and H.C. Kuo, "Fuzzy Sets Based Contingency Ranking", IEEE Trans. on Power Systems, 7, 1182-1188 (1992).         [ Links ]
14. Yager, R.R., "Multiple Objective Decision Making Using Fuzzy Sets", Int. J. Man-Machine Studies, 9, 375-382 (1977).         [ Links ]
15. Youssef, H.K., and R. Hackam, "Dynamic Solution of Distribution Planning in Intermediate Time Range", IEEE Trans. on Power Delivery, PWRD-2, 341-348 (1988).         [ Links ]

Received: September 13, 2004
Accepted: February 13, 2007
Recommended by Subject Editor: Julio Braslavsky