Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.37 n.4 Bahía Blanca oct. 2007
A transversely isotropic law for the determination of the circumferential young's modulus of bamboo with diametric compression tests
L. A. Torres1, K. Ghavami2 and J. J. García1
1 Escuela de Ingeniería Civil y Geomática, Universidad del Valle - Colombia;
ltorres@univalle.edu.co, josejgar@univalle.edu.co
2 Civil Engineering Department, Pontifícia Universidade Católica do Rio de Janeiro - Brasil
ghavami@civ.puc-rio.br
Abstract — Bamboo is a highly anisotropic natural material widely used in structural applications. A transversely isotropic constitutive equation is proposed here as the simplest law able to capture main anisotropic features of bamboo. Diametric compression tests were undertaken to determine the circumferential Young's modulus of two bamboo species based on the transversely isotropic model and using a simple formula of elasticity, validated with finite element analyses considering true and simplified geometries. Results showed that the use of idealized geometries and simple formulas provided a good estimation of the circumferential modulus. Load-deformation curves displayed a softening behavior which was approximated with two straight lines. Using the slope of the first line, the circumferential moduli were found to be 485 ± 172 MPa and 1685 ± 132 MPa for Guadua angustifolia and Phyllostachys pubescens, respectively. For Guadua angustifolia the circumferential modulus showed a significant increase with height, registering values of 651 ± 153 MPa for the top, 465 ± 126 MPa for the middle and 344 ± 98 MPa for the bottom parts of the culm. For Phyllostachys pubescens the circumferential modulus was independent of the length of the specimen. Results confirm the significant anisotropic behavior of bamboo, that should be considered in a reliable mechanical model of the culm.
Keywords — Bamboo. Anisotropy. Elastic Constants. Finite Elements. Testing Procedures.
I. INTRODUCTION
Bamboo is an anisotropic and heterogeneous material (Ray et al., 2005; Ghavami, 2005) with physical and mechanical properties well suited for structural applications. In addition, the economical and environmental advantages of bamboo have been widely documented in several studies (Ghavami, 2005; Cleuren and Henkemans, 2003). These characteristics have stimulated its uses and have waken the interest of the scientific community to extend and optimize structural applications, which include: steel substitution in structural concrete elements, concrete slabs with bamboo permanent shutter forms (Ghavami, 2005), temporary scaffolds, structural columns (Chung et al., 2005; Chung and Yu, 2002) and reinforcement elements in bahareque walls (González and Gutiérrez, 2006).
The bamboo culm is a structure formed by a hol-low cylinder reinforced with transversal diaphragms appearing at variable distances along its length (Fig. 1). The regions near the transversal diaphragms (nodes) have an external diameter slightly larger than that of the inter-nodal regions. The thickness of the bamboo wall remains almost constant in the inter-nodal regions and increases near the nodes. In addition to these geometric variations and similar to various types of wood, the anisotropy of bamboo is characterized by high mechanical properties in the axial direction, which contains fiber reinforcement, versus low mechanical properties in the transverse directions, without fiber reinforcement.

Figure 1. Geometric characteristics of the bamboo culm.
Experimental studies for the mechanical characterization of bamboo have focused mainly on the determination of the longitudinal elasticity modulus, which is currently the only elastic constant with a bamboo-specific standardized protocol (ISO/DIS, 2001). One of these studies was accomplished by Ghavami and Marinho (2005) who conducted compression and tensile tests instrumented with bidirectional strain gages to determine the longitudinal elasticity modulus and longitudinal-circumferential Poisson's ratio of specimens from the bottom, middle and top part of bamboo culms, obtaining average results of 13.85 GPa and 0.30 for the elasticity modulus and the Poisson's ratio respectively. Méndez and Vallecilla (2003) conducted wave propagation tests on specimens of Guadua angustifolia finding a value of 13.69 ± 1.76 GPa for the longitudinal Young´s modulus. Li (1999) finds from bending tests a Young's modulus for the Phyllostachys pubescens equal to 8.68 and 13.4 GPa for one and five year old bamboo, respectively. Sánchez and Prieto (2002) adapted the ASTM D 198 timber standard to obtain from bending tests a shear modulus of 644 ± 280 MPa for Guadua angustifolia. As to the knowledge of the authors, no experiments have been conducted to determine the circumferential or radial Young's modulus of bamboo. One of the reasons may be the difficulty to prepare specimens in the circumferential or radial directions given the relatively small thickness of the wall.
A transversely isotropic constitutive law was adopted here in order to consider the anisotropy of bamboo. It is hypothesized that a transversely isotropic law for bamboo is able to capture main anisotropic features of the material. Based on this model, an experimental procedure was carried out for the determination of the circumferential Young's modulus from diametric compression tests. The proposed test, designed to suit bamboo geometry, is the first reported procedure for the determination of the circumferential elasticity modulus. Finite element models were used to simulate the tests and to evaluate the influence of geometric irregularities in the results.
II. MATERIALS AND METHODS
To describe the anisotropy of bamboo a transversely isotropic elastic constitutive equation was adopted here. This law is characterized by five independent elastic constants which are the Young's moduli in the axial (Ez) and circumferential directions (Eφ), the out-of-plane (νzφ) and in-plane (νrφ) Poisson's ratios, and the shear modulus (Gzφ) (Fig. 2).
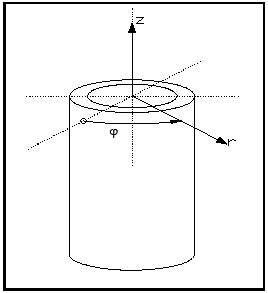
Figure 2. Definition of the cylindrical coordinate system.
To determine the circumferential Young's modulus, bamboo rings were subjected to diametric compressive tests (Fig. 3 and 4). In this test, bamboo rings were mainly working in the plane of isotropy, and thus, as a first approximation, the deflection ν0 was calculated using the following formula developed for isotropic materials (Roark and Young, 1975)

|
(1) |
where P is the diametric load, R is the average radius, A is the area of the cross section under bending (given by L × h from Fig. 3), As is the shear area of area "A", and I is the moment of inertia of area "A" about axis 1 (Fig. 3). The first, second and third terms of Eq. 1 represent the deflection due to axial force, bending moment and shear force, respectively. A preliminary parametrical analysis showed that for radius/thickness ratios (R/h in Fig. 3) higher than 4.3 the shear contribution was less than 5% of the total deflection, which is consistent with the geometry of bamboo specimens (Tables 1, 2). Hence, the third term of Eq. 1 was neglected so that the calculation of the slopeS of a force-deflection experimental curve allowed the determination of Eφ as

|
(2) |
The diametric compression test was undertaken with two groups of specimens. The first group was intended to study the variation of Eφ with height of Guadua angustifolia (Guadua). Three rings were taken from each location (top, middle and bottom) of six culms, to complete a total of 54 rings. The rings had an external diameter of 110 ± 10 mm, a thickness of 12 ± 3 mm and were cut to have their length equal to one fourth of their external diameters (Table 1). The second group, intended to study the influence of the length of the rings in the value of Eφ, consisted of 12 rings cut from the bottom part of a single Phyllostachys pubescens stem (Moso bamboo). Three rings were cut with each of the following lengths: one fourth, one half, three fourths and once their external diameter (D). These rings had an external diameter of 87 ± 1 mm and a thickness of 8.0 ± 0.2 mm (Table 2).

Figure 3. Ring subjected to diametric compressive load.

Figure 4. Experimental setup for the second group of rings and details of the fracture patterns.
Table 1. Dimensions of rings from group 1 - Average values and standard deviation (S.D.).
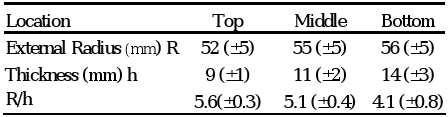
Table 2. Dimensions of rings from group 2 - Average values and standard deviation (S.D.).

Different testing devices were used for the two groups. The first group was tested in a soil unconfined compression tester (EI25-3602 Soil test) in which the rate of deflection was controlled manually at an approximate speed of 1 mm/min. Load readings were taken when deflection reached multiples of 0.127 mm (0.005 in). Deflection and applied load were measured with a precision of 0.025 mm and 1.5 N. The second group was tested in an automatically operated universal machine (Instron 5500 R) (Fig. 4).The crosshead speed was set up at 1 mm/min and load acquisition was made every two seconds. Deflection and applied load were measured with a precision of 0.01 mm and 0.1 N. All rings were loaded until failure (Fig. 4) with the direction of the diametric load taken randomly. For the first group, the t-student test for paired data was used to determine statistical significant difference. For the second group, the traditional t-student test was used to determine statistical significant difference.
Seven 3-D finite element models were analyzed in order to understand the stress distribution in the rings and to test the validity of Eq. 2, given the influence of geometric irregularities and length of the rings. The geometries of three modeled rings were taken from specimens cut from the top, middle and bottom parts of bamboo stem 2 of group 1 with aspect ratios R/h equal to 6.0, 5.1 and 3.2. Four rings from group 2 were also modeled, one for each of the characteristic lengths, i.e. one fourth, one half, three fourths and once their external diameter. To take into consideration geometric irregularities, the meshes of these four rings were created over digitalized images of their traced cross sections. Given the approximately plane configuration of the protocol, elastic constants different than the circumferential elasticity modulus do not have a great influence in the results. Therefore, for all models the elastic constants were defined as follows: The longitudinal Young's modulus was assumed to be 13.9 GPa and the out-of-plane Poisson's ratio was taken as 0.31 according to experimental values reported by Ghavami and Marinho (2005). The out-of-plane shear modulus was set as 640 MPa (Sánchez and Prieto, 2002). Since there are no reported values for the in-plane Poisson's ratio, this elastic constant was made equal to the out-of-plane Poisson's ratio, i.e. 0.31.
All models used eight-node transversely isotropic brick elements (Algor Ins., Pittsburgh, USA). To simulate the boundary conditions (Fig. 5), all degrees-of-freedom of the nodes located in the external face of the inferior part of the ring were constrained. Lateral stability of the models was achieved by constraining lateral displacements of the nodes located in the interior face of the superior part of the ring. A prescribed displacement of 2 mm was assigned to all of the nodes located in the exterior face of the superior part of the ring (Fig. 5) and the Young´s modulus Eφ was obtained adjusting the experimental and the finite element force-deflection curves.
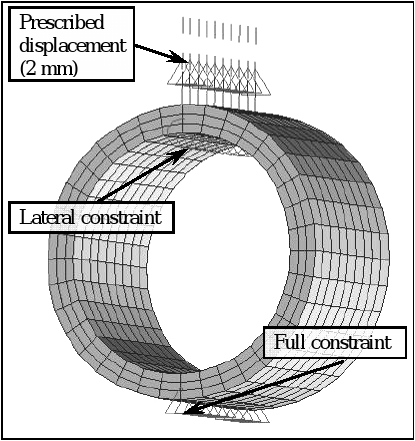
Figure 5. Boundary conditions for the diametric compression models.
III. RESULTS
All experimental force-displacement curves displayed a slight softening behavior which was approximated in this study using two straight lines (Fig. 7, 8). Excellent correlations were obtained for both lines (R2 greater than 0.98 for all Guadua and Moso Bamboo specimens) indicating that this is a good approximation.
A. Guadua rings
It was not possible to test five of the 54 specimens due to small fissures in the internal side of the rings' wall. Three of these five specimens were from the bottom part of bamboo culm number 5, which impeded the estimation of a circumferential elasticity modulus representative for that position. The other 2 fissured rings belonged to the middle part of culms 2 and 6.
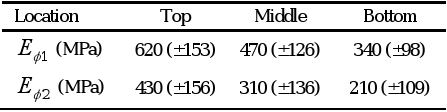
A very consistent trend was observed in the variations of the Young's modulus from the bottom to the top of the culms, with the average Young's modulus from the top nearly two fold that from the bottom and 34% higher than that from the middle portion. Results from each location were statistically different than those from the others positions (Table 3).
Table 3. circumferential elasticity moduli obtained from the first line (Eφ1) and second line (Eφ2) of Guadua angustifolia force-displacement curves.
The average value of the circumferential modulus (485 ± 172 MPa) was only 3.5 % the Young's modulus in the longitudinal direction (Ghavami and Marinho, 2005) which is consistent with the anisotropy of the material with fibers aligned in the longitudinal direction. The ratio 0.035 between circumferential and longitudinal moduli is in the range documented for different types of wood, (U.S. Dept. of Agriculture, 1999) which shows relations between transversal (radial and circumferential) and longitudinal moduli varying from 0.015 to 0.163.
B. Moso bamboo rings
No statistical difference was found between the circumferential modulus of rings with different lengths (Table 4). The average circumferential Young's modulus (1.69 ± 0.13 GPa) was around 3.5 fold that obtained for Guadua angustifolia. The coefficient of variation of the circumferential moduli (Eφ1) for the 12 samples of Moso bamboo was 7.8%.
Table 4. circumferential elasticity moduli obtained from the first line (Eφ1) and second line (Eφ2) of Moso bamboo force-displacement curves.
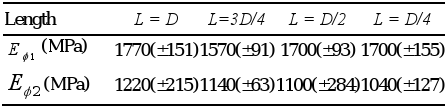
The ratio between the circumferential modulus of this study and the longitudinal modulus of 13.85 GPa (Ghavami and Marinho, 2005) was 0.122 which is in the range documented for different kinds of wood (U.S. Dept. of Agriculture, 1999).
C. Finite Element Models
Finite element models show that both, compression and tension circumferential stresses, appear in each section of the rings (Fig. 6). This indicates that the bending moments induced by the applied compressive force mainly determine the response of the ring. Alternatively, the models also showed that, regardless of their R/h ratios, the maximum normal tensile stress in the circumferential direction was always located in the inner surface, just below the applied compressive force (point A in Fig. 4, 6), and where initial fissures often appeared during the experiments.
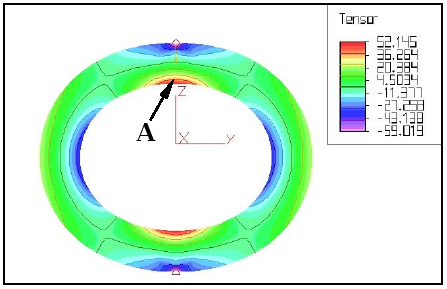
Figure 6. Deformed ring and contours of circumferential stresses showing maximum values at the inner surface in the axis of applied load (Point A).
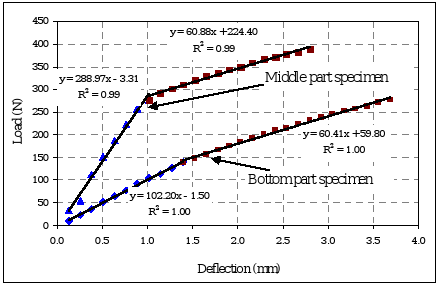
Figure 7. Typical load-deflection curves. Specimens from the middle and bottom parts of culm 4, exhibiting a softening effect.
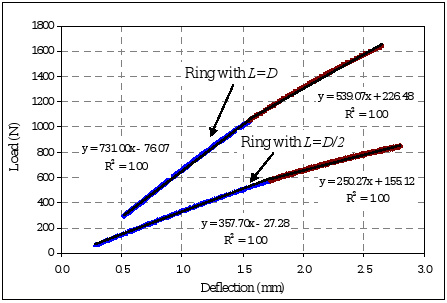
Figure 8. Typical load vs. deflection curves of specimens from group 2 with L = D and L = D/2.
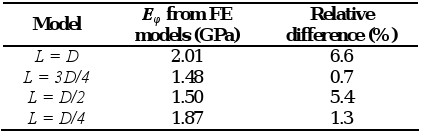
The Young's moduli obtained with the finite element models considering the geometric irregularities of the Moso Bamboo specimens (table 5) had a maximum difference of 7% with respect to those obtained with Eq. 2.
Table 5. Young's modulus Eφ from the finite element models and relative difference with respect to value obtained with Eq. 2.
IV. DISCUSSION
A transversely isotropic constitutive equation has been proposed in this study for the mechanical characterization of bamboo. This means that the plane perpendicular to the fibers is assumed to be isotropic and therefore the Young's modulus in the circumferential direction is equal to that in the radial direction In addition, the in-plane shear modulus, i.e. the shear modulus in the plane of isotropy, is related to the circumferential modulus and the in-plane Poisson's ratio through the standard formula valid for isotropic materials (Beer and Johnston, 1992). This law is only an approximation of the true anisotropy of bamboo and wood, the latter of which has been characterized in many studies by an orthotropic model. However, the transversely isotropic model captures the main anisotropic feature of bamboo which is the high value of the longitudinal Young's modulus compared to the circumferential, radial and shear moduli. This anisotropy is also present in all types of wood for which the longitudinal modulus has been found to be more than ten fold the value of other elastic constants (U.S. Dept. of Agriculture, 1999).
On the other hand, the hypothesis that the circumferential modulus is equal to the radial appears to be consistent with the longitudinal alignment of the fibers and experimental studies for different types of wood which report values for the circumferential modulus of the same order of magnitude than those of the radial modulus (U.S. Dept. of Agriculture, 1999). This general anisotropic behavior, i.e. a higher longitudinal modulus and similar values along radial and circumferential directions, can be captured by the transversely isotropic model proposed here, which represents a high improvement respect to an isotropic model. The coefficient of variation (7.8%) of the circumferential modulus for the 12 samples of moso bamboo, tested with a randomly oriented diametric load, can be considered low if one takes into account the irregularities of the rings and the heterogeneity of natural materials. This is also consistent with the transversely isotropic model. No measurements have been reported for the in-plane shear modulus of bamboo (i.e. radial-tangential shear modulus), which according to the transversely isotropic model proposed here should be approximately half the circumferential modulus. Again, the in-plane shear modulus reported for various types of wood is approximately half of the Young's moduli documented for the radial and circumferential directions, which is consistent with the transversely isotropic model. However, more analytical and experimental studies have to be undertaken to fully determine the advantages and limitations of the constitutive equation.
The softening behavior in the diametric tests (Fig. 7, 8) may be attributed to either, small cracks which may have occurred in point A (Fig. 4) described before, or finite displacements which may have produced nonlinear behavior in the stress-strain curve. However, the analysis of a nonlinear finite element model considering finite deformations did not show this nonlinear behavior for the current load levels. The average normal stress at point A at the load level between the first and the second line was 1.8 ± 0.1 MPa for Guadua and 15.4 ± 2.7 MPa for Moso Bamboo, which may be considered as reference values for crack initiation. Brittle failures were observed in all rings, which is consistent with the lack of circumferential fiber reinforcement.
Differences among locations obtained in the circumferential modulus for Guadua are very consistent, which is a new finding of this study. Another experiment to determine bamboo longitudinal Young's modulus and out-of-plane Poisson's ratio along the height of Guadua culms does not show differences among locations (Ghavami and Marinho, 2005). However, Li (1999) undertook experiments with bamboo species Phyllostachys pubescens and found a higher longitudinal compression modulus for the top compared with the middle and bottom portions of the culm, and no significant differences in the tensile longitudinal modulus. Unlike the tensile longitudinal modulus, both, the circumferential modulus and the compression longitudinal modulus, depend mostly on the properties of the matrix, which suggests that the findings of this study are consistent with those of Xiaobo Li and that the elastic properties of new matrix from the top part of a bamboo stem are higher than those of the old matrix from the bottom part. These results also appear to be consistent with those by Lo et al. (2004) who finds a higher compressive strength at the top compared to the bottom part of culms from Mao Zhu and Kao Zhu bamboos.
The small differences found between the results obtained with a simplified geometry and those of the finite element models suggest that irregularities in the wall thickness as well as length of the specimens play a minor role in the mechanical behavior of bamboo rings under diametric load.
V. CONCLUDING REMARKS
A transversely isotropic model has been proposed in this study as the simplest model intended to capture the main anisotropic feature of bamboo, i.e. the high value of the longitudinal modulus compared to the elastic moduli in other directions.
A simple test has been proposed to determine the effective average circumferential modulus, which is an elastic property not easily measured for bamboo, given the small thickness of the wall.
The circumferential modulus of Guadua angustifolia from the top part of the culm was higher (620 ± 153 MPa) than that of the middle (470 ± 126 MPa) and bottom (340 ± 98 MPa) portions of the culm. The ratio between the average circumferential modulus obtained here and the longitudinal modulus of Guadua angustifolia documented in other studies was 0.035 which is in the range of ratios documented for different types of wood. The circumferential modulus for Guadua (485 ± 172 MPa) resulted to be lower than that for Moso bamboo (1685 ± 132 MPa).
No significant differences were found in the circumferential modulus for Moso bamboo considering specimens with different lengths. In addition, irregularities in the wall thickness of the culm did not greatly affect the determination of the circumferential Young's modulus.
The finite element method was a useful tool to validate results obtained with simple formulas of strength of materials using idealized geometries. Other finite elements models can be implemented to determine the mechanical response of the bamboo culm under different types of loading conditions. This procedure may result in a better design of bamboo structures and a more reliable determination of the stress distribution in structural joints considering the main anisotropic feature of bamboo.
AKNOWLEDGEMENTS
Thanks are due to the Universidad del Valle, Cali, Colombia and the Pontifícia Universidade Católica do Rio de Janeiro, Brazil, as main supporting institutions.
REFERENCES
1. ASTM D 198. "Standard methods of static tests of timber in structural sizes". [ Links ]
2. Beer, F.P., and E.R. Johnston, Mechanics of Materials, McGraw-Hill, New York, 1992. [ Links ]
3. Chung, K.F., W.K. Yu and S.L. Chan, "Axial buckling of bamboo columns in bamboo scaffolds", Engineering Structures, 27, 61-73 (2005). [ Links ]
4. Chung, K.F., and W.K. Yu, "Mechanical properties of structural bamboo for bamboo scaffoldings", Engineering Structures, 24, 429-442 (2002). [ Links ]
5. Cleuren, H.M., and A.B. Henkemans, "Development of the bamboo sector in Ecuador: Harnessing the potential of Guadua angustifolia", J. Bamboo and Rattan, 2, 179-188 (2003). [ Links ]
6. Ghavami, K., "Bamboo as reinforcement in structural concrete elements", Cement and Concrete Composites, 27, 637-649 (2005). [ Links ]
7. Ghavami, K., and A.B. Marinho, "Propriedades físicas e mecânicas do colmo inteiro do bambu da espécie Guadua angustifólia", Revista Brasileira de Engenharia Agrícola e Ambiental, 9, 107-114 (2005). [ Links ]
8. González, G., and J. Gutiérrez, "Structural performance of bamboo 'bahareque' walls under cyclic load", J. of Bamboo and Rattan, 4, 353-368 (2006). [ Links ]
9. ISO/DIS 22157 International Standard, Determination of physical and mechanical properties of bamboo (2001). [ Links ]
10. Li, X., "Physical, chemical, and mechanical properties of bamboo and its utilization potential for fiberboard manufacturing", Louisiana State University- Master Thesis (1999). [ Links ]
11. Lo, T.Y., H.Z. Cui and H.C. Leung, "The effect of fiber density on strength capacity of bamboo", Material Letters, 58, 2595-2598, (2004). [ Links ]
12. Méndez, L., and C. Vallecilla, "Sistema Constructivo de Casas en Tierra Timagua: Análisis Experimental de Conexiones". Undergraduate Thesis. Universidad del Valle. Cali - Colombia (2003). [ Links ]
13. Ray, A.K., S. Mondal, S.K. Das and P. Ramachandrarao, "Bamboo - A functionally graded composite -correlation between microstructure and mechanical strength". J. of Materials Science, 40, 5249-5253 (2005). [ Links ]
14. Roark, R.J., and W.C. Young, Formulas for Stress and Strain. McGraw-Hill, 5th ed. (1975). [ Links ]
15. Sánchez, J., and E. Prieto, "Comportamiento de la Guadua angustifolia sometida a flexión". Undergraduate Thesis. Universidad Nacional de Colombia (2002). [ Links ]
16. U.S. Department of Agriculture, Forest Service. Wood Handbook: Wood as an engineering material (1999).
[ Links ]
Received: January 2, 2007
Accepted: February 28, 2007
Recommended by Subject Editor: Alberto Cuitiño














