Servocontrol of machine-tools: a review

R. L. Hecker^1,3, G. M. Flores¹, Q. Xie² and R. Haran^1,3

¹ Facultad de Ingeniería, Universidad Nacional de La Pampa, Calle 9 y 110, (6360) Gral. Pico, Argentina. hecker@ing.unlpam.edu.ar
² George W. Woodruff School of Mechanical Engineering, Georgia Institute of Technology
801 Ferst Drive N.W., Atlanta, Georgia 30332-0405, USA
³ CONICET

Abstract — Servocontrol loops are an important component in the control architecture of machine tools. Such loops manage the axes based on requirements of velocity, position, and acceleration. The success of modeling and control techniques applied to this level sets the basis for production of parts with high quality as well as cycle time reduction.
First, an introduction is presented for the three mayor control levels: adaptive control, interpolation, and servocontrol level. The drives and transmission components for traditional machine tools as well as for precision machines are discussed; including compareison between systems, such as linear versus rotational electric actuators. Then, relevant control techniques, such as Zero Phase Error Tracking Control (ZPETC) and Cross Coupling Control (CCC), are presented with experimental results. After that, modern control strategies to mitigate the effect of nonlinearities, model uncertainties, and perturbations are studied. Furthermore, the problem of High Speed Machining (HSM) is also reviewed. In addition, precision control for precision machining is examined. At the end, the future tendency of Open Architecture Systems (OAS) that allows the implementation of any control strategy in machine tools is presented.
Finally, it is included a summary on: electric and mechanical components, control strategies, precision machining, high speed machining, and a discussion on why new control techniques are not available in commercially machine tools.

Keywords — Machine Tools; Servo Control; Tracking Control; Contour Error; Open Architecture Systems.

I. INTRODUCTION

Machine tools are an important part of many manufacturing processes with a growing demand of part quality and cost reduction. To achieve these objectives and given a shortage of expert manufacturing equipment operators over the past decade, machine tools have incorporated technology to automatize the process (Liang et al., 2004). The introduction of the first Computer Numerical Control (CNC) machine was in the early 1970's, when most of the digital hardware from the Numerical Controlled (NC) machine was replaced by a dedicated computer.

The control architecture of a modern machine tool can be divided in three levels: servocontrol, interpolation, and adaptive control, as Figure 1 shows (Koren, 1997).

Figure 1: Machine Tools Control and Monitoring - General Scheme (Koren, 1997).

Adaptive control sets the programmed parameters (feeds and speeds) in order to pursue a given criterion or to minimize a given cost function using measured or predicted output process variables (force, power, and surface roughness among others). The two most used adaptive control strategies are Adaptive Control Optimization (ACO) and Adaptive Control with Constrain (ACC) (Sathyanarayanan, 1986). Different sensors and signal processing techniques can be applied to the online study of surface integrity, dimensional accuracy, tool conditioning and chatter detection (Liang et al., 2004). Furthermore, different control techniques for machining force control, chatter suppression, burr and chip formation, cutting temperature and tool conditioning were reported in Liang et al. (2004).

The interpolator level sets the coordinated movements among the axes of motion in order to achieve the tool trajectory. The desired trajectory is divided in discrete points using a given criterion at the interpolation level and then the command for each axis is generated. The interpolation level can be classified as Linear Interpolation, Circular Interpolation, and Complex Surface Interpolation. Real Time Curve Interpolation, such as Geometric Adaptive Control (GAC), is used when the tool trajectory is on-line adapted to compensate for possible geometric errors, as the ones induced by tool deflection (Koren, 1997)

Servocontrol loops control the axes of the machine based on requirements of velocity, position and acceleration. Traditionally, the dynamics of each axis in a machine tool is represented as a second order system for which well-known techniques are applied, such as PID (Proportional-Integral-Derivative) controllers (Koren, 1997). However, the action of these simple controllers can be degraded by process perturbations, model uncertainties and non-linearities, which require sophisticated techniques and innovative hardware to achieve higher control requirements.

This paper presents:

An exhaustive review of feed drives and transmission components, traditional control techniques in the servocontrol loops, and new control strategies to overcome problems related to machine tools such as external disturbances and model uncertainties;

An review of control techniques used in high speed machining and in precision machining;

An introduction to open architecture systems developed for machine tools, and finally,

A discussion with future trends in the area.

II. FEED DRIVES AND TRANSMISSION COMPONENTS

Electrical drives used in machine tools are DC brushed, DC brushless motors, AC synchronous and AC induction motors. The brushless DC (BLDC) motor is in increasing use with the advances in semiconductor power technology (Srinivasan and Tsao, 1997). The BLDC is preferred over the conventional electric drives for the following reasons (Famouri, 1992): the absence of brushes reduces maintenance and eliminates undesired commutation effects, the low rotor inertia increases the mechanical response, higher power to weigh ratios are obtained using rare-earth magnetic materials; and the armature winding is placed in the stator, resulting in a more efficient heat dissipation. The disadvantages are higher cost than conventional electric motors and the requirement of complex controllers due to coupled nonlinearities (Krause, 1984).

Linear power transmissions are used with electric motors both to convert rotational to linear motion and to achieve speed reduction. A typical device used in machine tools is the ballscrew-nut transmission, which can achieve precise repeatable motions; however, backlash reduction and rigidity is achieved by preloading the nut at the expenses of increasing friction and wear. Gears can also be used in machines, which require further speed reduction; however, ballscrews and gears present low first natural frequency that limits the performance of the closed-loop. The case of high speed machining is especially important because a closed-loop bandwidth of at least 100 Hz must be achieved, whereas for typical CNC machines it is in the order of 25 Hz (Smith, 1999). Therefore, the natural frequencies from the mentioned mechanical components could degrade the closed-loop performance in high speed machines.

All the transmission elements can be eliminated in machine tools by using direct linear drivers. Servo-controlled linear hydraulic actuators have been used especially for high force levels but they require a hydraulic system that demands more maintenance than electric devices. Linear electric motors represent an attractive choice because in general the bandwidth is higher than in ballscrew-motor systems; however, they are still under research due to force ripple, stick-slip friction, quantization errors and the direct effect of cutting forces on the motor degrading the control performance (Choi et al., 1999; Elfizy et al., 2005).

Piezoelectric actuators are a special kind of direct actuators feasible for high resolution (10 nm) and for stroke lengths of a few hundred microns together with high actuator stiffness (300 N/micron; Kouno, 1984) and high bandwidth (100 Hz; Elfizy et al., 2005); however, they present problems such as nonlinearity, hysteresis and DC drift. This actuator has been used in diamond turning and conventional machine tools for error correction due to spindle eccentricity. Inchworm actuators work with piezoelectric layers in series that clamp and move in a coordinated way to generate long strokes, but they have poor velocity control and low bandwidth.

The ultimate alternative is to combine coarse and fine drive stages to generate large strokes with high resolution by adopting the merit of each drive stage. An example was presented by Elfizy et al. (2005), where a linear motor and a piezoelectric actuator were combined in a servo stage for milling applications. Results of this implementation are presented in Figure 2 where the Dual Stage Feed Drive (DSFD) presents a considerable error reduction in comparison with the response of the Linear Motor (LM) alone if a ramp command is applied. Similarly, Chen and Dwang (2000) used a piezoelectric built into the nut of a ballscrew to control the nut preload and to produce fine positioning adjustment. A key issue in dual stages is to determine the way they work together complementary (Elfizy et al., 2005). If the fine drive stage has a higher bandwidth than the coarse drive, then the setpoint is split into two frequency components and the fine drive must follow the higher frequencies. On the contrary, if there is no significant difference between the bandwidths, the error from the positioning of the coarse stage must be feed as a set point to the fine drive.

Figure 2: Ramp response and positioning error for a dual stage (Elfizy et al., 2005)

The machine slides are another factor with a significant influence on motion control. Box ways can absorb vibrations and support elevated levels of force because they are an integral part of the machine base and they have a large contact area. However, they have problems with the stick-slip friction phenomenon as is described in the next section. Instead, linear guides present smoother movements but they are less rigid and cannot effectively transmit vibrations to the base as box ways do. The rigidity of linear guides can be improved by preloading but at expense of increasing friction.

Aerostatic bearing technology can be used for high precision motion with low loads, such is the case of measuring machines. However, they present a lack of damping in the feed direction due to the lack of friction. The no-damping limits the freedom of tuning a cascade controller such as a PI compensator. The state space approach allows freely pole placement even with no-damping, but it presents problems in the implementations phase. Regarding this fact, Schmidt (1997) applied a cascade state space control to a linear motor with air bearing with satisfactory results, combining the virtues of state space control and cascade control.

III. RELEVANT MACHINE TOOL CONTROLS

The feed drives control the position and velocities of the machine axes in accordance with commands generated by the CNC. The requirements for a feed drive include: control over a wide range of speeds, precise control of position under disturbances, rapid response, and precise coordination of multiple axes for contouring operations.

A general drive controller structure for a single axis is a cascade type compensator with an inner velocity loop and an outer position loop. Design criteria are based on achieving a certain closed position control loop bandwidth, steady state accuracy, and rejection of disturbances. Additionally, a feedforward compensator can be added to reduce the tracking error. A special kind of feedforward controlled is the Zero Phase Error Tracking Controller (ZPETC) based in zero pole cancellation with special care in non-minimal systems (Tomizuka, 1987).

Contouring accuracy is an important performance measured in multi-axial operations. A common technique to reduce the contour error is by cross-coupling control (CCC). This technique was introduced by Koren (1980) and a modified version with variable gains was also presented by Koren and Lo (1991). This controller basically uses feedback information from all the axes and generates a correction signal for each axis based in an optimal compensation law, Figure 3.

Figure 3: Cross Coupling Controller

From experiments carried on a milling machine interfaced with a computer (Koren, 1997), the following interesting conclusions were pointed based on the response of Figure 4:

The ZPETC presents ability to track nonlinear contours such as circles but with poor disturbance rejection, additional error due to model uncertainties, and poor tracking of linear references.

The PID controller results in significant overshoot in transient state and poor tracking at high feedrates.

CCC presented the best result by comparison with the other controllers for both linear and circular cuts.

Figure 4: Experimental results of a straight-line motion of different servo-controllers (Koren, 1997).

Most of these control techniques are fixed gain controllers, where the compensators are tuned for nominal conditions. Adaptive techniques can reduce the effect of nonlinearities and time variable parameters in the system, such as friction and cutting forces respectively. Some of these techniques developed in the last years are introduced in the next section.

IV. PERTURBATIONS AND MODEL UNCERTAINTIES

Friction plays a major role in reducing performance in machine tools controllers. A typical curve of friction force versus velocity for two solid surfaces sliding together separated by a lubricate film is presented in Figure 5 (Amstrong-Helouvry et al., 1994). The curve is dominated by static friction at zero velocity (Regime I) and an effective fluid film can not be generated at very low velocities (Regime II), increasing the velocity a layer of lubricant is generated (Regime III) with the consequent drop in the friction force, and at higher velocities the force is dominated by viscous friction (Regime IV). From the curve is clear that the main drawback of friction is at low velocities and during changes of direction, where stick-slip can occur due to the stribeck effect.

Figure 5: Stribeck friction curve (Amstrong-Helouvry et al., 1994)

Some attempts to compensate friction were based on off-line parameter identification for friction models and the implementation of compensation techniques based on these models, such as feedforward compensation (Tung et al., 1993), and state feedback regulations (Johnson and Lorenz., 1992). These approaches can reduce the problem but inaccuracies in the friction model and dependence of dynamic friction on machine conditions can deteriorate the response; furthermore, the friction model validation is time consuming.

To overcome these problems, on-line techniques can be implemented such as an adaptive velocity control scheme with on-line parameters estimation, including a Coulomb friction parameter, as presented by Yang and Chu (1993). The controller consisted of a friction compensator and a PID controller, whose gains were adjusted adaptively in terms of estimated parameters. Another example is the implementation of a disturbance-observer-based algorithm for the nonlinear friction compensation (Iwasaky et al., 1999), where the estimator was based on a nonlinear friction model.

Hecker and Liang (2002) presented a Repetitive Control to follow a linear trajectory in plunge grinding at very low velocity, in the order of 1 mm/min. This trajectory was generated by commanding the table position with a ramp signal generated by sending small steps every 5 sampling times. This way, the friction influence (Stick-slip) can be treated as a perturbation with constant period, that is the time between ramp input steps. Under this condition, a technique such as repetitive control can be used to mitigate the perturbation and improve the response to follow each individual step. The controller used was the internal model repetitive controller in digital domain composed of an internal signal generator and a ZPETC, as proposed by Tomizuka et al. (1989). Figure 6 shows the commanded ramp position with a slope of 0.7 mm/min, where the repetitive controller shows an initial time in learning to mitigate the friction effect. The error was reduced to ±2μm after 2 s, using a linear scale with 0.5μm resolution.

Figure 6. Position response for a ramp reference (top) and the corresponding position error (bottom), Hecker and Liang 2002).

The major source of uncertainties in machine tools control is not only friction, but also inertia and external disturbances like cutting forces during machining. Yao et al. (1997) proposed an adaptive robust control where a superior performance is achieved in terms of both the transient error and the final tracking accuracy in presence of uncertainties.

The tracking behavior of a direct drive design is quite sensitive to disturbances and model parameter variations due to the lack of a transmission unit (Srinivasan and Tsao, 1997; Van den Braembussche et al., 2001). Alter and Tsao (1994) examined the issue of stable turning using linear DC motor feed drives. They concluded that stability is not a problematic issue for turning, and that attention should be focused on issues such as disturbance rejection and trajectory tracking. Alter and Tsao (1996, 1998) also examined H_∞ optimal feedback and feedforward controllers as they apply to linear DC motors. In addition to position feedback, cutting force feedback was examined. It was found that, in a practical system, both H_∞ optimal position feed-back and H_∞ optimal force feedback could increase dynamic stiffness. H_∞ optimal feedforward controllers were found to be limited in practical systems, particularly in bandwidth, due to their modeling uncertainty. A MIMO (Multiple Input Multiple Output) H_∞ controller was applied in a linear motor for end milling process by Choi et al. (1999), and it showed lower tracking error than a conventional PID controller over a wide range of cutting forces and feed rates.

Van den Braembussche et al. (2001) have performed controller design and experimental validations for a linear motor feed drive axis. They compared the robustness of the control with respect to load changes up to 300% in terms of tracking performance. They demonstrated experimentally the robustness of the discrete time sliding mode control and enhanced the performance of H_∞ controller using an improved weighting function. Another application of sliding mode control to high precision control of linear motor is shown by Li and Wikander (2004). They proposed a so-called model reference sliding mode control approach which converts servo problems to simple regulator problems. The method is also capable of compensation of unknown disturbances, such as friction, without using any complicated friction modeling and corresponding on-line identification techniques. However, the controller is not capable of completely eliminating the friction effect in the case of reference trajectories crossing zero velocity.

Adaptive robust control (ARC) theory is a more aggressive approach in dealing with robustness in terms of both stability and performance. The theory developed by Yao et al. (1997) for advanced motion control has experimentally demonstrated that a better control performance is achieved than with existing nonlinear robust control (e.g., sliding mode controls) or nonlinear adaptive controls in a number of motion control applications. Recently, he made a thorough introduction of a variety of the ARC approaches and examined their merits and drawbacks (Yao, 2004). Among all the proposed ARC variants, many have been successfully applied to precision motion control of linear motors with epoxy core (Xu and Yao, 2001), and iron core (Xu and Yao, 2000). Figure 7 displays the tracking errors for high-acceleration high-speed point-to-point motion trajectory implemented on an Anorad linear motor (Xu and Yao, 2000). As can be seen, Desired Compensation ARC (DCARC) controllers achieve much better performance than PID does. Considering force ripple compensation (DCARC1) resulted in a better tracking performance. The effectiveness of the proposed ARC algorithms in reducing the tracking error under the influence of model parametric uncertainty has been demonstrated by extensive comparative experiments.

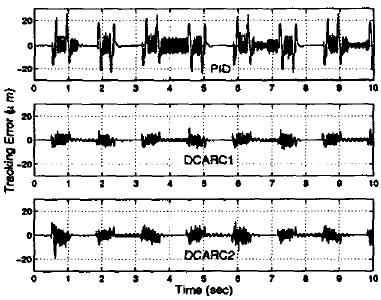
Figure 7. Tracking errors for high-acceleration high-speed trajectory implemented on a linear motor, Xu and Yao(2000).

V. HIGH SPEED MACHINING CONTROL

Milling operations are used extensively in the automotive and aerospace industry. Particularly, in the aerospace industries there are applications where light and large structures are milled from solid blocks of aluminum, titanium and magnesium, removing as much as 95% of the original material. In these situations it is clear the importance of maximizing the material removal rate (MRR) to diminish the cycle time. The MRR is in direct relationship with cutting parameters such as chip thickness, cutting speed and feeding speed, which are in turn limited by several factors associated with the performance and structure of the machine and to the cutting tool life. This last factor diminishes exponentially with increasing cutting speed, which is generally associated to the machine spindle. However, new tool materials, like tungsten carbide, have minimized this effect in aluminum machining. This allows machining aluminum parts at cutting speed limited only by the machine capacity and of their spindle. In this way it is possible to increase the material removal rate by increasing the spindle speed and maintaining the chip thickness constant.

The machining process carried out at increased cutting speeds is termed High Speed Machining (HSM) and it is generally accepted withing the range of spindle speeds superior to 10000 rpm, and as much as 40000 rpm as was reported by Smith (1999). In HSM is necessary to increase the feed between the cutting tool and the workpiece, proportionally to the increased spindle speed. This represents a problem, particularly in the machining of parts that require short and repetitive movements demanding high accelerations profiles. To accurately follow feeding commands with 1g of acceleration or more a bandwidth of 100 Hz in the position control loop is necessary. This value exceeds the bandwidth of conventional controllers (P, PI or PID) in low speed CNC machines, which is in the range of 10 Hz to 25 Hz applying accelerations less than 0.2 g. This means that the benefit of machining at high speeds cannot be achieved by simply attaching a high spindle to a conventional machine. In such cases there would occur high tracking errors because the closed loop control system is not able to follow the rapidly varying position commands.

Most of the control techniques used in low speed machines are based on second order models. However, due to the higher bandwidth required for HSM the models must be augmented with higher order dynamics, with the consequent application of more complex control techniques. In Smith (1999) a feedback control system was developed that effectively deals with the structural dynamics of the feed drive system to achieve the wide bandwidth required for high-speed milling. In this research the feed control system, using a conventional recirculating ballscrew transmission, was stabilized for a wide bandwidth control using a poles and zeros canceling compensator for the structural modes. This control strategy achieved a position bandwidth of 100 Hz, which allows to follow 2g acceleration profiles with 30 m/min feed-rates. The use of linear motors in high-speed machines eliminates the necessity of balls-screw transmission and its associate structural dynamics. These motors generally allow to increase the position control bandwidth, however they are costly and have high sensitivity to cutting force and mass variation in the table.

Erkokmaz and Altintas (2000) presented a systematic approach for designing a controller for HSM considering a second order model and using a pole placement controller (PPC) with disturbance cancellation (DC) in order to counteract the detrimental effects of friction, cutting force and drive parameter variations. A feedforward controller (ZPETC) was used to enlarge the bandwidth to 30 Hz, larger values will increase the sensibility to noises and unwanted high frequency oscillations. Additionally, the tracking errors due to friction transient at the corner and arc quadrant are reduced by precompensating for the expected friction forces (FFIRC, feed forward friction compensation). Finally, authors verify experimentally the contribution of each component of the control scheme in the contouring precision and demonstrate the global performance in high speed machining tests with and without material removal, as is presented in Table 1.

Table 1. Summary of experimental of tracking and contouring (Erkokmaz and Altintas, 2001b).

Renton and Elbestawi (2000) adopted a different approach for the high-speed servo drive control. They drop the assumption that the tracking error for a perfectly tuned controller is produced generally by command actions that overcome the speed or acceleration limits of one or more axes. To reduce this source of error they find the capacities of each axis and modify the tool feed in such a way to avoid these limits. They presented an algorithm to determine the maximum feed for an arbitrary trajectory without exceeding the capacities of any axis, called Minimun-Time Path Optimization (MTPO). They demonstrate that the machining time can be reduced significantly without decreasing the contouring precision if the entire capability of the system is used, instead of fixed acceleration and velocity limits. The algorithm was computationally tested as a complement for different controllers and a significant improvement was observed in the performance. The test was achieved without the presence of disturbance and with a precise plant model. Among the analyzed controllers, the ZPETC was the simplest and has shown the best results. Also, the research presents the results achieved with a modified version of a traditional PD controller. It demonstrates a significant improvement and suggests the application of this modified PD controller in combination with Minimum-Time Path Optimization for existing machines tools.

The performance achieved with Generalized Predictive Control (GPC) was exceptionally good; however, because this controller does not have knowledge of the system limitations, either performs suboptimal to a disturbance or saturates. Another disadvantage is the computational time that generally is often too large to be useful for high-speed controllers using current microprocessors. Finally, the Minimum-Time Tracking Controller, MTTC, is presented which turns the attention to the main error sources in high-speed machining like amplifier limits, system inertia, and damping. The controller behavior was computationally efficient and robust for a step command as Figure 8 shows. The biggest advantage that this controller presents is the considerably superior disturbance rejection.

Figure 8: Response of PD, MTTC and GPC controllers to a 0.001m step input (Renton and Elbestawi, 2000).

In high speed machining, high accelerations excite the machine structure up to high frequencies, thereby exciting the structure's modes of vibration. These structural vibrations need to be damped if accurate positioning or trajectory tracking is required (Symens et al., 2004). For this purpose, many kinds of techniques to avoid structural vibrations have been developed, such as initial value compensation (Iwasaki et al., 2004), acceleration feedback (Chen and Tlusty, 1995), shaping of input commands (Jones and Ulsory, 1999; Fortgang et al., 2005), limiting the jerk commands (Erkorkmaz and Altintas, 2001), and notch filter (Erkorkmaz and Altintas, 2005). To deal with the varying vibration modes, Gain-scheduling control (Symens et al., 2004) and the H_∞ control (Iwasaki et al., 2002) have been presented the fast-response and high-precision machine tool drives. All these techniques will be examined one by one.

To ensure high-precision positioning in machine tool drives, residual vibration resulting from the repeated fast transient must be suppressed. For this purpose, Iwasaki et al. (2004) presented a novel Initial Value Compensation (IVC) methodology on the basis of pole-zero cancellation. The effectiveness of the proposed compensation has been verified by numerical simulations and experiments using a positioning device of industrial machine tools.

Input Shaping is a feedforward control technique for reducing vibrations in computer controlled machines. The method works by creating a command signal in such a way that eigenfrequencies of the mechanical system cannot be excited. Jones and Ulsory (1999) proposed an input shaping strategy in the discrete time domain that reduces the self-induced structural vibrations in a CMM. The control strategy is developed by establishing the relationship between controller input shaping techniques and traditional notch filtering methods. They have addressed issues on both robustness and multiple mode vibrations. Their experimental results show a 50 percent reduction in the peak-to-peak magnitude of structural vibrations as compared to unshaped bang-bang trajectories. In a recent research, Fortgang et al. (2005) have successfully applied a nonlinear command shaping technique to a micro-mill operated at a high speed to achieve high accuracy by canceling vibrations caused by structural flexibility.

Notch filters are used frequently to suppress undesirable resonances and oscillations. Erkorkmaz and Altintas (2005) examined a control strategy for precision tracking controller design for high speed feed. They considered rigid body dynamics in the plant and attenuated the lowest structural resonance with a notch filter. The proposed control algorithm has been implemented in a Fadal VMC 2216 three axis machining center. It was shown that the rigid body based design with notch filtering has a simple form and provides comparable stability, tracking, and disturbance rejection properties.

To deal with the ballscrew-nut flexibility problem, Chen and Tlusty (1995) have investigated the effect of acceleration effect in improving both the transient response to the NC command and the response of the driven mass to the cutting force.

Reference trajectory generation plays a key role in the computer control of machine tools. Erkorkma and Altintas (2001b) presented a quintic spline trajectory generation algorithm that produces continuous position, velocity, and acceleration profiles. By limiting the jerk of the reference trajectory, the excitation of the natural modes of the mechanical structure or servo control system is avoided.

All of the above mentioned efforts towards vibration suppression did not take parameters uncertainty of vibration modes or varying structural eigenfrequencies into account. However, Symens (2004) argued that these structural eigenfrequencies are not constant but dependent on the position of the tool in its workspace. To ensure high performance motion control, these varying resonances should be taken into account. In this research, they used a gain-scheduling control approach to deal with a structural beam with varying eigenfrequencies. Furthermore, not all vibration modes are known in advance and their parameters are not fixed. Aiming at resonant vibration suppression, a robust compensator design has been presented by Iwasaki et al. (2002). As a result, the desired positioning with a robust performance can be achieved. The effectiveness of the proposed controller has been verified by experimental results using a positioning system of industrial machine tools.

VI. HIGH PRECISION CONTROL

As technology advances and devices become smaller and/or more complex, the need for high precision machining processes is becoming increasingly important. To establish a precision machining process for micro-assembly and Micro-Electro-Mechanical-Systems (MEMS) for example, precision motion is very crucial. With the continuing demand on high performance, the tolerance requirements on the motion subsystem, in terms of precision, are more and more increasing.

As mentioned, friction is also a major challenge to the control system design including friction for high precision motion, say submicron positioning. Ro et al. (2000) investigated submicron positioning in the presence of friction. They developed a bristle-type nonlinear contact model and implemented it for submicrometer motion. For submicrometer positioning, they proposed a proportional-derivative (PD) control scheme with a nonlinear friction estimate algorithm, and its performance is compared with that of a PID controller. For tracking, they added a disturbance observer to reject external disturbances and to improve robustness. They have shown that the proposed controller has a consistent performance in positioning with less than 1.5% of steady-state error in the submicrometer range by experiments. For tracking performance, the proposed controller shows good and robust tracking with respect to parameter variations. Also, for precision positioning in the presence of friction, Mao et al. (2003) studied an aerostatic slide system driven by a DC motor with brushes that introduce friction. They investigated the microdynamic behavior of friction. Instead of designing two controllers for the different dynamics, they presented a single-step precision positioning using a high-gain controller designed according to the macrodynamics. They demonstrated by experiments and simulation results that the PID controller can provide a sufficiently high loop gain. In point-to-point positioning for step inputs from millimeter size down to submicrometer size, the positioning error is within ±2nm and the response dynamics is satisfactory.

VII. OPEN ARCHITECTURE SYSTEMS

The implementation of various sensors and control strategies at all levels requires the development of open architecture systems with a great deal of flexibility in hardware and software. Figure 9 summarizes the tendency of open architecture systems and its components (Pritschow et al., 2001).

Figure 9: Future tendencies in Open Architecture Systems

Schofield and Wright (1998) presented the MOSAIC-PM (Machine Tool Open System Advanced Intelligent Controller for Precision Machining) and they defined that an open architecture system must have the following attributes: Flexibility, integration and standardization. Flexibility is related to internal issues of an open architecture controller, those of modularity and scaleability. Integration is the idea of interoperability. Standarization is a requirement that encompasses portability and interchangeability. These concepts were also treated by Anderson et al. (1993) in their Open System Architecture Standard (SOSAS).

Examples of laboratory computer based systems were a machining center based on sun/VME bus/Real-time Unix/C architecture by Schofield and Wright (1998), and a grinding center based on PC/dSPACE/Control Desk by Hecker and Liang (2000).

Among the commercially available systems are: Delta Tau PMAC-NC, IBH PA 8000, Galil DMC 1000, Creonics MCC VME, Adept Series A, Aerotech Unidex 31, New controllers From Hewlett-Packard, Cincinnati Milacron and Fedal, CIMplus for Application program, Typ3 osa from Bosch Automation. These commercial systems present advantages with respect to traditional CNC systems; however, they are not as flexible as laboratory computer-based systems and they present a low level of flexibility, integration and standardization.

VIII. DISCUSSION

Extensive work has been done at the servo-control level in machine tools. There is a tendency to study new mechanical systems, such as airbearing that reduce non-desired effects like friction, and to develop new motors and electronic technologies to control the motors in an accurate and efficient way, such as brushless DC motors. New control techniques have been tested, like adaptive control, to manage nonlinearities, time dependant effects and model uncertainties.

However, most of these approaches are laboratory setups with a lack of sufficient transference to the machine tools manufacturers. Part of this is due to the low flexibility of the controllers installed in the CNC machines to implement new control strategies. Another reason could be that traditional controllers, like PID and PDF (Pseudo Derivative Feedback), are easily tuned and are highly robust (Yen and Chang, 2004).

There are two recent areas in machining that present new challenges:

High speed machining: the traditional models must be augmented with higher order dynamics due to the higher bandwidth required for HSM, with the consequent requirement of more complex control techniques specially to mitigate the effects of exciting high frequency modes.

Precision machining: especially important for MEMS (Micro Electro-Mechanical Systems) fabrication, where precise motion with precisions below the micrometer level must be reached. In this area there is a tendency to manufacture small machine tools, called mesoscale machines, to reduce the influence of thermal deformation. Special positioning sensors, like strain gauge and precise interferometric linear scales, must be used in conjunction with high resolution motors, like piezoelectric actuators. Therefore, control techniques must be developed to overcome nonlinearities (friction, hysteresis, ripple, etc.) and perturbations present in these systems.

REFERENCES
1. Alter, D.M. and T.-C. Tsao, "Stability of turning process with actively controlled linear motor feed drives", J. of Engineering for Industry, 116, 298-307 (1994).         [ Links ]
2. Alter, D.M. and T.-C. Tsao, "Control of linear motors for machine tool feed drives: design and implementtation of H_∞ optimal feedback control", ASME Journal of Dynamic Systems,Measurements, and Control, 118, 649-655 (1996).         [ Links ]
3. Alter , D.M. and T.-C. Tsao, "Control of linear motors for machine tool feed drive: experimental investigation of optimal feed forward tracking control." ASME Journal of Dynamic Systems and Control, 120, 137-141 (1998).         [ Links ]
4. Amstrong-Helouvry, B., P. Dupon and C. Canudas de Wit, "A Survey of Models, Analysis Tools, and Compensation Methods for the Control of Machines with Friction", Automatica, 30, 1083-1138 (1994).         [ Links ]
5. Anderson, B.M., J.R. Cole and R.G. Holland, "An Open Standard for Industrial Controllers", Manufacturing Review, 6, 180-191 (1993).         [ Links ]
6. Chen, J.S. and I.C. Dwang, "A Ball Screw Drive Mechanism with Piezo-electric Nut for Preload and Motion Control", International Journal of Machine Tools & Manufacture, 40, 513-526 (2000).         [ Links ]
7. Chen, Y. and J. Tlusty, "Effect of low-friction guide-ways and lead-screw flexibility on dynamics of high-speed machines", CIRP Annals - Manufacturing Technology, 44, 353-356 (1995).         [ Links ]
8. Choi, Ch., T.-Ch. Tsao and A. Matsubara, "Control of Linear Motor Machine Tool Feed Drivers for End Milling: Robust MIMO Approach", Proceeding of the American Control Conference, San Diego, 3723-3727 (1999).         [ Links ]
9. Elfizy A.T., G.M. Bone and M.A. Elbestawi, "Design and control of a dual-stage feed drive", International Journal of machine Tools and Manufacture, 45, 153-165 (2005).         [ Links ]
10. Erkorkmaz, K. and Y. Altintas, "High speed CNC system design, Part I: Jerk limited trajectory generation and quintic spline interpolation", International Journal of Machine Tools and Manufacture, 41, 1323-1345 (2001a).         [ Links ]
11. Erkokmaz, K. and Y. Altintas, "High Speed CNC System Design. Part III: High Speed Tracking and Contouring Control of Feed Drives", International Journal of Machine Tools and Manufacture, 41, 1637-1658 (2001b).         [ Links ]
12. Erkorkmaz, K. and Y. Altintas, "Precision tracking controller design for high speed feed drives", Proceedings of ASME International Mechanical Engineering Congress & Exposition, Orlando, FL, USA, 80498 (2005).         [ Links ]
13. Famouri, P., "Control of a Linear Permanent Magnet Brussels DC Motor via Exact Linearization Methods", IEEE Transaction on Energy Conversion, 7, 544-551 (1992).         [ Links ]
14. Fortgang, J., W. Singhose, J. De Juanes Marquez and J. Perez, "Command shaping for micro-mills and CNC controllers", Proceedings of the American Control Conference, 7, 4531-4536 (2005).         [ Links ]
15. Hecker, R. and S. Liang, "Low feed control in plunge grinding under friction effect", Japan-USA Symposium on Flexible Automation, Hiroshima, Japan, 65-66 (2002).         [ Links ]
16. Hecker, R.L., and S.Y. Liang, "Power Feedback Control in Cylindrical Grinding Process", ASME International Mechanical Engineering Congress and Exhibition, Orlando, Florida, DSC 69, 713-718 (2000).         [ Links ]
17. Iwasaki, M., T. Shibata and N. Matsui, "Disturbance-Observer-Based Nonlinear Friction Compensation in Table Driven System", IEEE/ASME Transaction on Mechatronics, 4, 3-8 (1999).         [ Links ]
18. Iwasaki, M., K. Seki and H. Hirai, "Fast-response positioning using H∞ control in machine tools", International Workshop on Advanced Motion Control, 46-51 (2002).         [ Links ]
19. Iwasaki, M., N. Hirose, M. Kawafuku and H. Hirai, "Residual vibration suppression using initial value compensation for repetitive positioning", Proceedings 8th IEEE International Workshop on Advanced Motion Control, 571-576 (2004).         [ Links ]
20. Johnson C.T. and R.D. Lorenz, "Experimental Identification of Friction and its Compensation in Precise, Position Controlled Mechanism", IEEE Trans. Ind. Applicat., 28, 1392-1398 (1992).         [ Links ]
21. Jones, S.D. and A.G. Ulsoy, "Approach to control input shaping with application to coordinate measuring machines", ASME Journal of Dynamic Systems, Measurement and Control, 121, 242-247 (1999).         [ Links ]
22. Koren, Y., "Cross-Coupled Biaxial Computer Control for Manufacturing Systems", ASME Journal of Dynamic Systems, Measurements and Control, 102, 265-272 (1980).         [ Links ]
23. Koren, Y., "Control of Machine Tool", Journal of Manufacturing Science and Engineering, 119, 749-755 (1997).         [ Links ]
24. Koren, Y. and C.C. Lo, "Variable-Gain Cross-Coupling Controller for Contouring", Annals of CIRP, 43, 371-374 (1991).         [ Links ]
25. Kouno, E., "A Fast Piezoelectric Actuator for Servo Correction of Systematic Errors in Precision Machining". Annals of CIRP, 33, 369-372 (1984).         [ Links ]
26. Krause, P.C., Analysis of Electrical Machinery, New Work, McGraw-Hill (1984).         [ Links ]
27. Liang, S.Y., Hecker, R.L. and R.G. Landers, "Machining Process Monitoring and Control: The State-of-the-Art", Journal of Manufacturing Science and Engineering, ASME, 126, 297-310 (2004).         [ Links ]
28. Li, Y.-F. and J. Wikander, "Model reference discrete-time sliding mode control of linear motor precision servo systems", Mechatronics, 14, 835-851 (2004).         [ Links ]
29. Mao, J., H. Tachikawa and A. Shimokohbe, "Precision positioning of a DC-motor-driven aerostatic slide system", Precision Engineering, 27, 32-41 (2003).         [ Links ]
30. Pritschow, G., Y. Altinas, F. Jovane, Y. Koren, M. Mitsuishi, S. Takata, H. Van Brussels, M. Weck, M. and K. Yamazaki, "Open Controller Architecture - Past, Present and Future", Annals of the CIRP, 50, 463-470 (2001).         [ Links ]
31. Renton, D. and M.A. Elbestawi, "High Speed Servo Control of Multi-axis Machine Tools", International Journal of Machine Tools and Manufacture, 40, 539-559 (2000).         [ Links ]
32. Ro, P.I.., W. Shim and S. Jeong, "Robust Friction Compensation for Submicrometer Positioning and Tracking for a Ball-Screw-Driven Slide System", Precision Engineering, 24, 160-173 (2000).         [ Links ]
33. Sathyanarayanan, G., "Adaptive Control of Grinding - Technology and Research", SME, Technical Paper: MR86-638 (1986).         [ Links ]
34. Schmidt, C., "A Comparison of Control Strategies for Feed-Drive Systems of Ultraprecision Machine Tools - Effect of Frictionless Air Bearing", IEEE International Conference on Power Electronics and Drive Systems, 1, 262-269 (1997).         [ Links ]
35. Schofield, S. and P. Wright, "Open Architecture Controllers for Machine Tools, Part1: Design Principles", ASME Journal of Manufacturing Science and Engineering, 120, 417-424 (1998).         [ Links ]
36. Smith, D.A., "Wide Bandwidth control of high-speed milling machine feed drives", PhD dissertation, University of Florida (1999).         [ Links ]
37. Srinivasan, K. and T.-C. Tsao, "Machine Tool Feed Drives and Their Control - A Survey of the State of the Art", Journal of Manufacturing Science and Engineering, 119, 743-749 (1997).         [ Links ]
38. Symens, W., H. Van Brussel and J. Swevers, "Gain-scheduling control of machine tools with varying structural flexibility", CIRP Annals - Manufacturing Technology, 53, 321-324 (2004).         [ Links ]
39. Tomizuka, M., "Zero Phase Error Tracking Algorithm for Digital Control", ASME Journal of Dynamic Systems, Measurement, and Control, 109, 65-68 (1987).         [ Links ]
40. Tomizuka, M., T.-C. Tsao, and K.-K. Chew, "Analysis and Synthesis of Discrete-Time Repetitive Controllers", Journal of Dynamic Systems, Measurement and Control, 111, 353-358 (1989).         [ Links ]
41. Tung E.D., G. Anwar and M. Tomizuka, "Low velocity Friction Compensation and Feedforward Solution Based on Repetitive Control", Journal of Dynamic Systems, Measurement and Control, 115, 279-284 (1993).         [ Links ]
42. Van den Braembussche, P., J. Swevers and H. Van Brussel, "Design and experimental validation of robust controllers for machine tool drives with linear motor", Mechatronics, 11, 545-562 (2001).         [ Links ]
43. Xu, L. and B. Yao, "Adaptive robust precision motion control of linear motors with ripple force compensations: theory and experiments", IEEE Conference on Control Applications, 1, 373-378 (2000).         [ Links ]
44. Xu, L. and B. Yao, "Adaptive robust precision motion control of linear motors with negligible electrical dynamics: Theory and experiments", IEEE/ASME Transactions on Mechatronics, 6, 444-452 (2001).         [ Links ]
45. Yang, Y.P. and J.S. Chu, "Adaptive Velocity Control of DC Motors With Coloumb Friction Identification", Journal of Dynamic Systems, Measurement and Control, 155, 95-101 (1993).         [ Links ]
46. Yao B., M. Al-Majed and M. Tomizuka, "High Performance Robust Motion Control of Machine Tools: An Adaptive Robust Control Approach and Comparative Experiments", Proceeding of the American Control Conference, Albuquerque, New Mexico, 2754-2758 (1997).         [ Links ]
47. Yao, B., "Advanced motion control: An adaptive robust control framework", Proceedings - 8th IEEE International Workshop on Advanced Motion Control, 565-570 (2004).         [ Links ]
48. Yen, J.Y. and H.M. Chang, "Performance Robustness and Stiffness Analysis on a Machine Tool Servo Design", International Journal of Machine Tools and Manufacture, 44, 523-531 (2004).         [ Links ]

Received: September 28, 2006.
Accepted: July 23, 2007.
Recommended by Subject Editor Julio Braslavsky.