Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. v.38 n.4 Bahía Blanca oct. 2008
The effects of radiation on unsteady mhd convective heat transfer past a semi-infinite vertical porous moving surface with variable suction
A. Mahdy
Math. Department Science, South Valley University, Qena, EGYPT
sci_eng@yahoo.com
Abstract — Numerical solutions for the effects of radiation on a MHD convective heat transfer past a semi-infinite porous plate with a magnetic field are obtained. It is assumed that the porous plate moves with a constant velocity in the direction of fluid flow, and the free stream velocity follows the exponentially increasing small perturbation law. The magnetic field acts perpendicular to the porous surface which absorbs the fluid with a suction velocity varying with time. The governing equations for the flow are transformed into a system of nonlinear ordinary differential equations by perturbation technique and then are solved numerically by using the shooting method. The effects of the various parameters on the velocity, temperature profiles as well as the surface skin-friction and surface heat transfer are illustrated graphically.
Keywords — Unsteady State. Radiation. Moving Surface. Magnetic Field. Suction.
I. INTRODUCTION
It is known that the effects of radiation on MHD flow and heat transfer problem have become more important industrially. At high operating temperature, radiation effects can be quite significant. Many processes in engineering areas occur at high temperature and a knowledge of radiation heat transfer becomes very important for the design of the pertinent equipment. Nuclear power plants, gas turbines and the various propulsion devices for aircraft, missiles, satellites and space vehicles are examples of such engineering areas. Raptis (1998) investigate the steady flow of a viscous fluid through a very porous medium bounded by a porous plate subjected to a constant suction velocity by the presence of thermal radiation. Bestman (1990) examined the natural convection boundary layer with suction and mass transfer in a porous medium. His results confirmed the hypothesis that suction stabilizes the boundary layer and allows the most efficient method in boundary layer control yet known. Abdus Sattar and Hamid Kalim (1996) investigated the unsteady free convection interaction with thermal radiation in a boundary layer flow past a vertical porous plate. Makinde (2005) examined the transient free convection interaction with thermal radiation of an absorbing emitting fluid along moving vertical permeable plate.
Chamkha (2004) assumed that the plate is embedded in a uniform porous medium and moves with a constant velocity in the flow direction in the presence of a transverse magnetic field. Raptis and Perdikis (2002) studied the unsteady free convection flow of water near 4 oC in the laminar boundary layer over a vertical moving porous plate. Soundalgekar and Patti (1980) studied the problem of the flow past an impulsively started isothermal infinite vertical plate with mass transfer effects.
Takhar et al. (1996) studied the radiation effects on MHD free-convection flow of a gas past a semi-infinite vertical plate. Seddeek (2000, 2001) studied thermal radiation and buoyancy effects on MHD free convective heat generating flow over an accelerating permeable surface with temperature-dependent viscosity in the case of steady state. The radiation effects on heat transfer over a stretching surface have been studied by Elbashbeshy (2000).
In spite of all these studies, the unsteady MHD convective heat transfer in the presence of radiation has received little attention. Hence, the main objective of the present investigation is to consider the case of a semi-infinite moving porous plate in a porous medium with the presence of radiation and constant velocity in the flow direction when the magnetic field is imposed transverse to the plate and subjected to variable suction. It is also assumed that an exponential variation with time is imposed to temperature.
II. MATHEMATICAL FORMULATION
We consider, unsteady flow of a laminar, incompressible fluid past a semi-infinite vertical porous moving plate embedded in a porous medium in the presence of radiation and subjected to a transverse magnetic field (Fig. 1). In our problem we assumed that there is no applied voltage which implies the absence of an electric field. The transversely applied magnetic field and magnetic Reynolds number are very small and therefore the induced magnetic field is negligible (Cowling, 1957). Viscous and Darcy's resistance terms are taken into account with constant permeability of the porous medium. The governing equations for our problem under the usual boundary layer approximation can be written as follows:
 | (1) |
 | (2) |
 | (3) |

Fig. 1. The sketch of the physical model
where û and  are the components of dimensional velocities in the
are the components of dimensional velocities in the  and
and  directions, respectively
directions, respectively  and
and  are the dimensional distances along and perpendicular to the plate, respectively qr is the radiative heat flux and
are the dimensional distances along and perpendicular to the plate, respectively qr is the radiative heat flux and  are the temperature and pressure. Properties ν, ρ,
are the temperature and pressure. Properties ν, ρ,  , α and β are the kinematic viscosity, density, permeability, the fluid thermal diffusivity, and thermal expansion coefficients of the fluid, respectively, assumed constant. Furthermore, σ, B and cp are the fluid electrical conductivity, magnetic induction and the specific heat at constant pressure, respectively.
, α and β are the kinematic viscosity, density, permeability, the fluid thermal diffusivity, and thermal expansion coefficients of the fluid, respectively, assumed constant. Furthermore, σ, B and cp are the fluid electrical conductivity, magnetic induction and the specific heat at constant pressure, respectively.
Moreover, the appropriate boundary conditions for the velocity and temperature fields are:
 | (4) |
where ûp is the wall dimensional velocity  , ε are constants, T0 a reference temperature.
, ε are constants, T0 a reference temperature.
The radiative heat flux qr under the Rosseland approximation has the form
 |
where δ is the stefan-Boltzman's constant and  is the mean absorption coefficient.
is the mean absorption coefficient.
From the continuity equation Eq. (1), it is obvious that the suction velocity normal to the plate is a function of time only and it can be taken in the form:
 | (5) |
where A is a real positive constant value, ε and εA are small real numbers less than unity, V0 is a scale of suction velocity which has non-zero positive constant. Outside the boundary layer, Eq. (2) gives
 | (6) |
On introducing the dimensionless quantities, (the partial differential equations are converted into dimensionless form)
 | (7) |
In view of Eqs. (5)-(7), the governing Eqs. (2) and (3) reduce to the dimensionless form:
 | (8) |
 | (9) |
where
 |
 |
The previous boundary conditions take the following dimensionless form:
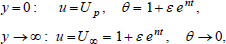 | (10) |
where Gr is the Grashof number, Mn is the magnetic field parameter, K is the permeability parameter, R is the radiation parameter, Pr is the Prandtl number, and θw is the temperature parameter.
III. SOLUTION PROCEDURE
Equations (8) and (9) represent a set of partial differential equations that can not be solved in closed form. However, it can be reduced to a set of ordinary differential equations that can be solved numerically. This can be done by representing the velocity and temperature as follows:
 | (11) |
Substituting Eq. (11) into Eqs. (8) and (9) and neglecting the coefficients of terms of O(ε2), we obtain the following pairs of equations for (f0,g0) and (f1,g1).
For zero order of ε
 | (12) |
 | (13) |
subject to the boundary conditions
 | (14) |
For O(1) of ε
 | (15) |
 | (16) |
subject to the boundary conditions
 | (17) |
The physical quantities of interest are the wall shear stress τw and the local surface heat transfer rate qw. These are defined as
 | (18) |
therefore, the local friction factor Cf is given by
 | (19) |
The local heat transfer coefficient in terms of Nusselt number can be expressed as
 | (20) |
or it can be also quantitatively evaluated by
 | (21) |
where  is the local Reynolds number.
is the local Reynolds number.
IV. RESULTS AND DISCUSSION
In the previous sections, we have formulated and solved the problem of the influence of radiation on an unsteady MHD convection heat transfer past a semi-infinite vertical porous moving plate. In the numerical computation, various values of the material parameters are used. In addition, the boundary condition y→∞ is approximated by ymax=6, which is sufficiently large for the velocity to approach the relevant stream velocity. A representative set of results is reported graphically in Figs. 2-16. These results are obtained to illustrate the influence of the radiation parameter R, the magnetic field parameter Mn, permeability parameter K, velocity of the plate Up, the dimensionless exponential index n, temperature parameter θw, Grashof number Gr, and Prandtl number Pr, on the velocity, temperature profiles, surface skin–friction and surface heat transfer in terms of Nusselt number.
Figures 2 and 3 show that the dimensionless velocity u and the dimensionless temperature θ increase as the radiation parameter R increases. Also, we observe that the magnitude of the stream wise velocity increases and the inflection point for the velocity distribution moves further away from the surface. In Fig. 4, the velocity is plotted for several values of Mn while R = 5.0. As seen in this figure, for a given value of magnetic field, the velocity profiles decrease monotonically with an increase in y. For small and large values of y, the effect of Mn is rather insignificant. Only when 0.5 < y < 4 the value of the velocity is reduced significantly depending on Mn.

Fig. 2. Effect of radiation parameter on velocity

Fig. 3. Effect of radiation parameter on temperature

Fig. 4. Effect of magnetic field on velocity
The velocity profiles for different values of plate moving velocity in the direction of fluid flow Up are described in Fig. 5 with R = 5.0. Although we have different initial plate moving velocities, the velocity decays to the constant value for the given material parameter.

Fig. 5. Effect of velocity of the plate on velocity
Figures 6 and 7 show that the dimensionless velocity u and the dimensionless temperature θ increase as the dimensionless exponential index n increases for the two cases R=0.0 and R = 5.0. The velocity profiles for different values of Grashof number Gr while R = 1.0 are described in Fig. 8. It is observed that an increase in Gr leads to an increase in the value of velocity. In addition, the curves show that the peak value of the velocity increases rapidly near the wall of the plate as Grashof number increases, and then decays to the relevant free stream velocity.

Fig. 6. Effect of n on velocity

Fig. 7. Effect of n on temperature

Fig. 8. Effect of Grashof number on velocity
Figure 9 depicts the temperature profiles as a function of the transversal coordinate y for various values of the Prandtl number, Pr. The numerical results show that the effect of increasing values of Prandtl number results in a decreasing thermal boundary layer thickness and more uniform temperature distribution across the boundary layer, while the values of the physical parameters are fixed at real constants, θw= 0.5, A = 0.5, ε= 0.2, the dimensionless exponential index n = 0.3, scale of free stream velocity Up = 0.5, Prandtl number Pr = 0.7 and t = 1.0 and for the two cases R = 0.0 and R = 3.0.

Fig. 9. Effect of Prandtl number on temperature
Figure 10 shows the velocity profiles for different values of the permeability parameter K. Clearly as K increases the peak value of velocity tends to increase with R = 0.0 and R = 2.0. The influence of the temperature parameter θw is plotted in Fig. 11. It is obviously that as θw increases leads to increase the thermal boundary layer thickness.

Fig. 10. Effect of K on velocity

Fig. 11. Effect of θw on temperature
The effect of time on velocity and temperature profiles is considered in Figs. 12 and 13. As it is clear from the figures that the peak value of velocity is increasing with increasing of time, the temperature increases in the range 0 ≤ y ≤ 2.614 and decreases when 2.614 ≤ y ≤ 6.

Fig. 12. Effect of time on velocity

Fig. 13. Effect of time on temperature
In addition, some graphs of the surface skin friction and surface heat transfer against the suction velocity parameter are reported in Figs. 14-18. The effect of radiation parameter on the surface skin friction and surface heat transfer illustrated in Figs. 14 and 15 respectively, and it is clear from these figures that both of skin friction and heat transfer increase with increasing the radiation parameter R. It has been observed from Fig. 16 that for a constant plate moving velocity Up with given material parameters, Mn, K, Pr, Gr, θw, and R = 0.0, 2.0 the effect of increasing values of suction velocity parameter A results in a slightly increasing surface skin friction for the lower values of Up. It is also evident that the surface skin friction decreases by increasing the plate moving velocity Up. As shown in Fig. 17, the skin friction on the porous plate increases by increasing the strength of suction velocity. It has been shown that for small values of the dimensionless exponential index n, the increment of surface skin friction has a gentle slope.

Fig. 14. Effect of R on the surface skin-friction

Fig. 15. Effect of R on the surface heat transfer

Fig. 16. Effect of Up on the surface skin-friction

Fig. 17. Effect of n on the surface skin-friction
Figure 18 illustrates the variation of surface heat transfer versus the suction velocity parameter A for several values of Prandtl number. Numerical results show that for given material parameters which are listed in figure, the surface heat transfer tends to decrease by increasing the magnitude of suction velocity for R = 0.0 and less decrease by increasing the magnitude of suction velocity when R = 2.0.

Fig. 18. Effect of Pr on the surface heat transfer
V. CONCLUSIONS
The plate velocity was maintained at constant value and the flow was subjected to a transverse magnetic field in the presence of radiation effect. The governing equations were developed and transformed into a system of nonlinear ordinary differential equations by perturbation technique and are solved numerically by employing the shooting method. The surface skin friction coefficient, surface heat transfer as well as the details of velocity and temperature profiles are presented for various values of parameters of the problem. The numerical results indicate that the temperature, skin friction and heat transfer increase as the radiation parameter increases. The velocity increases with the increase in radiation parameter, the exponential index, porous medium, Grashof number and plate moving velocity, while it decreases as the magnetic field parameter increases.
REFERENCES
1. Abdus Sattar, M.D., and M.D. Hamid Kalim, "Unsteady free-convection interaction with thermal radiation in a boundary layer flow past a vertical porous plate", J Math Phys Sci. 30, 25-37 (1996). [ Links ]
2. Bestman, A.R., "Natural convection boundary layer with suction and mass transfer in a porous medium", Int J Energy Res, 14, 389-396 (1990). [ Links ]
3. Chamkha, A.J., "Unsteady MHD convective heat and mass transfer past a semi-infinite vertical permeable moving plate with heat absorption", Int J Eng Sci., 42, 217-230 (2004). [ Links ]
4. Cowling, T.G., "Magnetohydrodynamics", Interscience, New York, (1957). [ Links ]
5. Elbashbeshy, E.M.A., "Radiation effect on heat transfer over a stretching surface", Can. J. Phys., 78, 1107-1112 (2000). [ Links ]
6. Makinde, O.D., "Free convection flow with thermal radiation and mass transfer past a moving vertical porous plate", Int Comm Heat Mass Transfer, 32, 1411-1419 (2005). [ Links ]
7. Raptis, A., "Radiation and free convection flow through a porous medium", Int Comm Heat Mass Transfer, 25, 289-295 (1998). [ Links ]
8. Raptis, A., and C. Perdikis, "Free convection flow of water near 4 oC past a moving plate", Forschung im Ingenieurwesen, 67, 206-208 (2002). [ Links ]
9. Seddeek, M.A., "The effect of variable viscosity on hydromagnetic flow and heat transfer past a continuously moving porous boundary with radiation", Int. Commun. Heat Mass Transfer, 27, 1037-1046 (2000). [ Links ]
10. Seddeek, M.A., "Thermal radiation and buoyancy effects on MHD free convective heat generating flow over an accelerating permeable surface with temperature-dependent viscosity", Can. J. Phys., 79, 725-732 (2001). [ Links ]
11. Soundalgekar, V.M., and M.R Patti, "Stokes problem for a vertical plate with constant heat flux", Astrophys Space Sci., 70, 179-182 (1980). [ Links ]
12. Takhar, H.S., R.S.R. Gorla and V.M. Soundalgekar, "Radiation effects on MHD free convection flow of a gas past a semi-infinite vertical plate", Int. J. Numer. Meth. Heat Fluid Flow, 6, 77-83 (1996). [ Links ]
Received: August 14, 2007.
Accepted: February 14, 2008.
Recommended by Subject Editor: Walter Ambrosini














