Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión On-line ISSN 1851-8796
Lat. Am. appl. res. vol.40 no.2 Bahía Blanca abr. 2010
ARTICLES
Convection in a rectangular channel with a flow of water in laminar-turbulent transition with high heat fluxes
N. Silin1,2, V. Masson1,2,3 y J. C. García2,3
1 CONICET; Comisión Nacional de Investigaciones Científicas y Técnicas; www.conicet.gov.ar
2 Instituto Balseiro, Universidad Nacional de Cuyo; Av. Bustillo 9500; 8400 - Bariloche- Argentina
3 CNEA-CAB; Comisión Nacional de Energía Atómica, Centro Atómico Bariloche; Av. Bustillo 9500; 8400 - Bariloche- Argentina.
silin@cab.cnea.gov.ar
Abstract - In this work we examine the phenomenon of laminar-turbulent transition in a heated rectangular channel under high heat fluxes and water as a working fluid. We use an experimental device that allows the electric heating of the walls and the measurement of its temperature through thermocouples housed beneath the surface. The results of this initial exploration clearly show the dependence of the convection coefficient on the heat flux through different mechanisms. In first place we can see an increase in the convection coefficient with the heat flux that is correctly predicted for laminar and turbulent flows by the Sieder-Tate correction. In second place, there was a clear change of behaviour that corresponds to the start of the transition to turbulence. The Reynolds number that corresponds to the departure from laminar behavior was independent of the heat flux in the walls within the conditions covered in this study.
Keywords - Convection; Hydrodynamic Transition; Heat Flux; Rectangular Channel.
I. INTRODUCTION
The main objective of this work is to investigate experimentally the thermo-hydraulic behaviour of a coolant channel similar to those found in the core of a nuclear research reactor. In this particular work we focus on the laminar to turbulent transition hydrodynamic regime with high wall heat fluxes. In our laboratory we began working on this issue starting with the RA6 research reactor power increase project. The RA6 is a pool type research reactor with a downward refrigerating flow forced by a pump. In the original design the flow between the fuel plates is in the laminar regime. A possible operation scenario involves a refrigerating flow between the fuel plates in a transition regime. This situation prompted us to make an experimental study in order to verify if the convection correlations developed for round tubes would apply to rectangular channels with high heat fluxes and regimes close to the transition to turbulence (Silin et al., 2007)
The pure hydrodynamic behaviour of rectangular channels has been studied under different conditions (Schlichting, 1979; White, 1991) resulting in a general consensus that even in micro-channels (Hartnett et al., 1965) the transition occurs for Reynolds numbers between 1800 and 2500. Above these Reynolds numbers the application of correlations for the turbulent regime is often accepted.
In contrast, the transition regime with heat transfer from the walls has not been studied experimentally in depth (Kandlikar et al., 2006; Boye et al., 2007). In an experimental study, Celata et al. (2002) have obtained the values of the transition Reynolds for capillary tubes of 0.13mm diameter, but even here the study is not detailed. It is a known fact that the transition regime is extremely sensitive to experimental conditions as the roughness of the walls and entry conditions (Schlichting, 1979; Wibel and Ehrhard, 2006). Similarly it is expected that in a heated section the varying properties of the fluid near the wall due to temperature gradient may also affect the transition to turbulence (Ozgen, 2004; Sameen and Govindarajan, 2007). In particular Ozgen, shows that in the boundary layer of external water flows the heat flux causes a delay the transition to turbulence. In contrast, the variation in the fluid density, that brings the natural convection phenomenon, appears to have a negligible effect in the transition regime in mini-channels (Delmastro et al., 2007).
Another important aspect is the occurrence of gas phase, even at temperatures below the temperature of saturation. This phenomenon is originated in the increase of the water temperature, causing a significant reduction of the air solubility in the water. The presence of dissolved gas may lead to the nucleation of gas bubbles in small pores of the walls. In general this phenomenon improves convection, however it has been shown experimentally that in some cases it may also affect the convection adversely, such as in micro-channels (Steinke and Kandlikar, 2004). To prevent the occurrence of this phenomenon, in this work we make sure that there is no presence of dissolved air in the water by boil degassing it.
Thus we can see that the heat transfer in rectangular channels under high heat fluxes can present various phenomena that are beyond the more traditional approaches and require special attention. Moreover, the combination of these factors has to be subject to a thorough experimental verification if reliable convection coefficients are needed as the interaction of factors is strongly non-linear in the transition regime.
In this work we will describe the design and operation of the test section developed to determining heat transfer coefficients under different conditions. This type of experimental devices presents different challenges in their thermo-mechanical design, mainly due to high heat fluxes that are pursued. We describe the solutions adopted and their limitations and finally present some preliminary measurements obtained with this test section. We will assess qualitatively the effects of the inlet Reynolds number, the wall heat flux, and propose a correction based on the use of the thermal conductivity of water at film temperature as opposed to the more traditional use of properties at bulk temperature.
A. Used parameters
In the study of heat transfer the main parameter of interest is the convection coefficient h defined as:
| (1) |
where q" is the heat flux per unit area, Tw is the surface temperature and Tm the flow bulk temperature. As the heat flux is uniform the fluid bulk temperature rise along the test section is expected to be linear within measurement error. Based on this characteristic the fluid bulk temperature Tm is calculated interpolating between the inlet and outlet temperatures. In the case of our study the heat input is homogeneously produced by Joule effect, by means of an electrical resistance tapes. The wall heat flux q" was derived from the heat balance based on the inlet and outlet temperature measurements for a given flow rate. In this way the effect of heat losses on the calculation of h are minimized. The fluid bulk temperature rise along the test section is expected to be linear because of the uniform heat flux, so Tm can be calculated as an interpolation between the inlet and outlet temperatures. Thus to calculate the convection coefficient h we need to measure: the flow input temperature Ti, the temperature of the wall at different points Tw(z) and the temperature output To. Additionally pressure and dissolved gas concentration of the water were controlled.
A number that is extremely useful for the comparison of results is the dimensionless form of the convection coefficient, the Nusselt number, which is defined as:
| (2) |
where k is the thermal conductivity of water and Dh is the hydraulic diameter of the test section.
When convection occurs under a significant variation of the fluid properties it affects the convection coefficient. A widely used correction to account for the variation of viscosity within the fluid is:
| (3) |
where µm y µw are the dynamic viscosities at bulk and wall temperatures respectively. This correction factor was first considered by Sieder and Tate (1936). In the laminar regime this correction takes into account the increase in the convection coefficient due to the lower viscosity close to the wall. This lower viscosity affects the laminar velocity profile of the flow and thus the convection. In this paper we introduce a further correction to account for the variation of the coefficient of thermal conductivity k due to the sharp temperature gradient close to the walls. We propose to use the value of kfilm corresponding to the film temperature (1/2(Tw+Tm)). The effect of the variation of the thermal conductivity is minor (the difference between the bulk and the film conductivity in the experiments is approximately 3%), but we want to show here that this factor is not taken into account by the Sieder-Tate correction. The Sieder-Tate correction was originally developed for oils in which have large viscosity indexes but relatively constant thermal conductivity. The Nusselt number then becomes:
| (4) |
For the study of convection in non developed flows a convenient nondimensional number is the Graetz (Gz), whose inverse is a nondimensional form of the entry length z.
| (5) |
According to Kakac and Yener (1995), the laminar hydrodynamic and thermal entry lengths, Lh and Lt respectively, for parallel plates with constant wall heat flux can be calculated as:
Lh = 0.011ReDh, Lt = 0.012RePrDh.
Following these expressions, at the beginning of the transition to turbulence, i.e. at Re of 2600, the hydrodynamic inlet length is about one fourth (0.16m) of the length of our test section and the thermal inlet is longer than the test section (0.85m).
II. EXPERIMENTAL DEVICE
The experimental device consists of a hydraulic circuit pressurized to 1.7 bar absolute pressure that allows regulating the temperature and flow of water through the test section (Figure 2). To avoid the flow pulsations and the drift of the water temperature at the entrance to the test section, it was decided not to use a pump. Instead water is driven from a reservoir that is pressurised using compressed air. The measurements are performed by batches of about half an hour each. Also the temperature and pressure as well as the contents of dissolved air and electrical conductivity of the water are relatively easy to control when the water is coming from a closed reservoir.
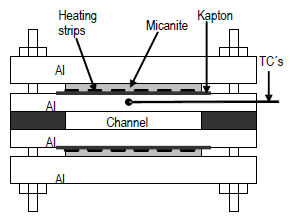
Figure 1: Cross section of the heated flow channel.

Figure 2: Experimental circuit outline
The hydraulic circuit is provided with PT100 temperature transducers to measure the temperature of the water incoming to and outgoing from the test section. The pressure is measured at the entrance to the section with a Jumo pressure transducer. The flow is obtained by means of an orifice plate and a DPcell that were carefully calibrated before performing the measurements.
A. Test section
The test section has a rectangular vertical geometry with a sharp inlet followed by 7cm (approximately 13 hydraulic diameters) of unheated channel. This length is followed by 62cm of electrically heated channel which provides a constant heat flux on both sides, and ends with an unheated channel length of 7cm. The passage area is a rectangle 60mm wide and 2.7mm thick.
The high heat flux that occurs in the plates of a nuclear reactor fuel is extremely difficult to reproduce in an experimental device. In this work we decided to heat the surface of the rectangular channel indirectly, that is using electrical resistance tapes to heat the test section. The heating tapes have a uniform resistivity and thus, provide uniform power. While this form of indirect heating is significantly complex in constructive terms, it allows greater geometric rigor. On the other hand it gives more flexibility in the election of direct current power supplies as it is relatively easy to modify the resistance value of heaters. The use of heating strips provides the channel wall a uniform heat flux. Axial conduction through the heating strips (0.1mm thick) is negligible and axial conduction along the test section walls is only relevant at the beginning and at the end of the test section.
Figure 1 shows the general outline of a cross section of the heated flow channel. In this figure it is shown how the heating tapes are electrically isolated from the walls of the canal through a thin sheet of Kapton. The Heating tapes are pressed by the backing plate through a layer of micanite which serves as thermal insulation. This pressure is important to minimize the thermal contact resistance between the tapes, the electrical insulation and walls of the channel.
Heat losses were estimated based on the comparison of the electrical power supplied to the test section with the heat balance based on inlet and outlet temperatures. Heat losses calculated as the difference between these two measurements have resulted in less than 10% for all measurements. In our design the thermocouples are inserted into transversal slots cut in one of the walls of the channel. The direct current power supply was a Bruker model BMN 70-700, which is robust and very reliable as to the accuracy of the current sup plied. In this study currents up to approximately 250 Amps were required.
The test section has a sharp entrance followed by 7cm (approx. 13 Dh) unheated channel length, it follows 62cm of electrically heated channel, which provides a constant heat flux on both sides, and finishes with an unheated channel of 7cm of length. Throughout the heated zone there are 8 type K thermocouples separated 80mm each, except for the latter that has a separation of 20mm with the previous one.
B. Measurement Methodology
To avoid the formation of bubbles on the wall and the consequent variation in the convection ratio, as a first step we let the water of the main reservoir degas by boiling it for about an hour. After the degassing the main reservoir is pressurized to the working pressure of 1.7 atm, this is done while the water is hot to minimize the possibility that air dissolves again in the water, and to avoid the creation of temperature gradients in the reservoir. A water flow rate through the test section is set and the temperature regulated by the cold water flow of the heat exchanger. After desired conditions are set up electrical power is applied to the heaters using a tension ramp of about 5 seconds to full power.
Temperatures are recorded by an acquisition card and stored in the memory of a PC to be processed later. We also record the tension between the heaters terminals, and the flow rate and inlet pressure to the test section.
III. EXPERIMENTAL RESULTS
The following results were obtained using degassed water as fluid at an input temperature of 20 ºC and a working pressure of 1.7 atm. The walls were applied a constant heat flux that was varied between 3.4 and 9.6 W/cm2. shows the Nusselt number as a function of the axial position for an entry Reynolds number of 1900 and various heat fluxes. This Nu is calculated with properties of the fluid at bulk temperature as Eq. (2). For a fixed z we see the Nu increases with the heat flux, which is an expected result. In the laminar regime this difference is due largely to the change in the velocity profile and in lesser degree to the higher conductivity of the hotter water near the wall.
Figure 4 shows the Nucorrected corrected as suggested in Eq.(3), as a function of the inverse Graetz number Gz-1 for the same measurements presented in Figure 3. In this case all the curves collapse in one unique curve for the extent of the laminar regime (up to Re ≈ 2300), which covers a different length depending on the power applied. In the laminar region a monotonous decay of the Nu is observed as the flow develops. This relatively long entry length is observed in the laminar regime while for turbulent flows the entry length is much shorter. Depending on the heat flux applied a departure from laminar behaviour is observed at different Gz numbers. This is due to the increase of the bulk temperature of the flow when heat is applied, lowering the viscosity and therefore increasing the Reynolds number along the channel. When the flow Reynolds number exceeds a certain threshold value it becomes unstable giving rise to an increase in the heat transfer coefficient and the Nu.

Figure 3: Nu calculated from properties at bulk temperature Tm as a function of axial position for an inlet Rein = 1900.
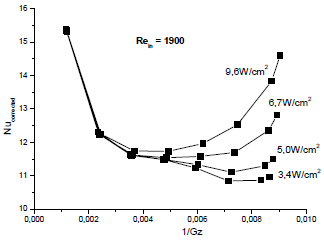
Figure 4: Corrected Nu vs. the Gz-1 for the same experimental data as shown in Fig. 3.
To study the influence of heat flux in the flow instabilization in Table 1 we show the Reynolds number at which the flow shows a departure from laminar behaviour as a function of the heat flux. The departure from laminar behaviour is determined from the convection coefficient measurements as the point where the Nusselt number shows an increase respect to the laminar case. As we can see the Reynolds number at which a departure from laminar behaviour occurs is roughly constant within the error margins and is about 2300 for an entry Re of 1900 and 2200 for an entry Re of 1800. At the same table we also show the axial position zd where this departure occurs. As expected the greater the heat flux the sooner the flow becomes unstable.
Table 1 Reynolds number and axial distance corresponding to the departure from laminar behaviour.

In Figure 5 we see the Nucorrected for different inlet Reynolds number, the heat flux is 6,7 W/cm2 and the inlet temperature Tin = 20 ºC. Also shown in thick line is the analytical result for a laminar flow assuming a combined hydrodynamic and thermal development, and in thin line the thermal development (Kays and Crawford, 1980). It is worth noting that the Nusselt number for fully developed laminar flow between parallel plates with constant properties is 8.23. From this figure we can see several different behaviors:
- The Nucorrected in the laminar regions depends on the inlet Re. This is expected because the length of channel without heating in the entrance is only 13 Dh, i.e. the flow is not hydrodynamically developed at the beginning of the heated zone, and the process of developing of the velocity profile depends on the Re number. If we compare, for instance, with the thin curve representing behaviour of a hydrodynamically developed flow, we see that the experimental points differ from this curve. This probably is because the profile is distorted by the entry conditions to the test section (sharp edges).
- For inlet Re numbers over 4300 the behaviour is clearly different from laminar in the whole heated part of the channel and entry length effects can not be observed. From this characteristic it can be assumed that the flow is already turbulent when entering the heated zone.
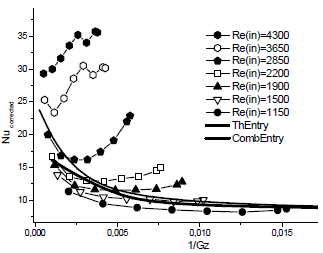
Figure 5: Nucorrected as a function of 1/Gz for different inlet Re, Tin = 20ºC, heat flux = 6,7 W/cm2.
Figure 6 shows the change of Nu with the inverse of the Gz number for different entry Re numbers and for each case, different values of heat flux, which are shown in Table 2. As we can see the curves of the Nucorrected calculated from experimental data collapse very well for each entry Re for the laminar cases.

Figure 6: Variation of the Nu number as a function of Gz-1 for different inlet Re and heat fluxes (see Table 2).
Table 2 Heat fluxes corresponding to measurements shown in Figure 6.

When the flow departs from laminar behaviour, it can be observed an increase in the values of Nu, being the increase stronger for the higher heat fluxes. Again this can be explained by the variation of the bulk Reynolds number along the channel, which is higher for the higher heat fluxes (viscosity varies with the increase of the mean temperature).
III. CONCLUSIONS
In the present work we have investigated experimentally the role of heat flux in the hydrodynamic transition to turbulent flow in a rectangular channel. The influence of the heat flux was studied using a corrected Nusselt number for different Reynolds numbers at the inlet to the test section and different heat fluxes. The method adopted for the correction of the Nusselt number proved to be appropriate, since it allows to collapse the laminar convection results in a single curve independent of the heat flux.
From the experimental Nucorrected we can clearly see the departure from laminar behaviour when either the axial distance or the heat flux is increased. This departure was always observed at a Reynolds number of about 2300 for the cases studied and its dependence on the heat flux seems to be weak.
The behaviour is clearly different from laminar across the whole channel for entry Re numbers greater than 4300.
As an additional result, it becomes apparent that the decline in the Nu with Gz-1 is different from the analytical model for the laminar case, this is probably due to a distorted velocity profile originated by the entry conditions of the test section.
REFERENCES
1. Boye, H., Y. Staate and J. Schmidt, "Experimental investigation and modelling of heat transfer during convective boiling in a minichannel", International Journal of Heat and Mass Transfer, 50, 208-215 (2007). [ Links ]
2. Celata, G.P., M. Cumo, M. Guglielmi and G. Zummo, "Experimental investigation of hydraulic and single-phase heat transfer in 0.130-mm capillary tube", Microscale Thermophysical Eng., 6, 85-97 (2002). [ Links ]
3. Delmastro, D., A.F. Chasseur, J.C. García, N. Silin and V.P. Masson, "Estudio de la influencia de la dependencia de las propiedades del agua con la temperatura en un flujo laminar descendente entre placas paralelas", XXXIV Reunión Anual AATN (2007). [ Links ]
4. Hartnett, J.P., J.C. Koh and S.T. McComas, "A comparison of predicted and measured friction factors for turbulent flow through rectangular ducts", J. Heat Transfer, 8484, 82-88 (1965). [ Links ]
5. Kakac, S. and Y. Yener, Convective heat transfer, 2nd Ed, CRC Press, (1995). [ Links ]
6. Kandlikar, S.G., S. Gaimella, D. Li, S. Colin and M.R. King, Heat transfer and fluid flow inminichannels and microchannels, Elsevier (2006). [ Links ]
7. Kays, W.M. and M.E. Crawford, Convective Heat and Mass Transfer, McGraw Hill, 100-128, (1980). [ Links ]
8. Ozgen, S. "Effect of heat transfer on stability and transition characteristics of boundary-layers", Int. J. of Heat and Mass Transfer, 47, 4697-4712 (2004). [ Links ]
9. Saneen, A, and R. Govindarajan, "The effect of wall heating on instability of channel flow", J. Fluid Mech., 577, 417-442 (2007). [ Links ]
10. Schlichting, H., Boundary layer theory, 7ª ed. Mc Graw -Hill, Nueva York (1979). [ Links ]
11. Sieder, E.N. and G.E. Tate, "Heat Transfer and Pressure Drop of Liquids in Tubes", Industrial and Engineering Chemistry, 28, 1429-1435 (1936). [ Links ]
12. Silin, N., V. Masson, A. Azcona, D. Delmastro, D. Mateos and S. Eckardt, "Determinación del coeficiente de convección del nuevo núcleo del RA6", XXXIV Reunión Anual de la AATN, Buenos Aires, Argentina, 19 al 23 de Noviembre (2007). [ Links ]
13. Steinke, M.E. and S.G. Kandlikar, "Control and effect of dissolved air in water during flow boiling in microchannels", Int. J. of Heat and Mass Transfer, 47, 1925-1935 (2004). [ Links ]
14. White, F.M., Viscous fluid flow, 2ª ed. Mc Graw -Hill, Nueva York (1991). [ Links ]
15. Wibel, W. and P. Ehrhard, "Experiments on Liquid Pressure-Drop in Rectangular Microchannels, Subject to Non-Unity Aspect Ratio and Finite Roughness", Proceedings of ICNMM2006 Fourth International Conference on Nanochannels, Microchannels and Minichannels, Ireland (2006). [ Links ]
Received: March 30, 2009.
Accepted: June 17, 2009.
Recommended by Subject Editor Walter Ambrosini.














