Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. vol.40 no.3 Bahía Blanca jul. 2010
The power series method in the effectiveness factor calculations
C.P. Filipich†, L.T. Villa‡ and R.O. Grossi‡*
† Mechanical System Group, FRBB, Universidad Tecnológica Nacional, 8000 Bahía Blanca, Argentina..
‡ Universidad Nacional de Salta - Facultad de Ingeniería. INIQUI - UNSa- CONICET. Buenos Aires 177, A 4402 FDC Salta, Argentina.
* Corresponding author. Tel: +543874255379, fax: +543874255351. E-mail address: grossiro@unsa.edu.ar
Abstract - In the present paper, exact analytical solutions are obtained for nonlinear ordinary differential equations which appear in complex diffusion-reaction processes. A technique based on the power series method is used. Numerical results were computed for a number of cases which correspond to boundary value problems available in the literature. Additionally, new numerical results were generated for several important cases.
Keywords - Diffusion And Reaction. Power Series Method.
I. INTRODUCTION
In the present work the exact analytical solutions are presented for a set of non-linear boundary value problems which arise in the analysis of steady diffusion-reaction processes. Several investigators have treated the heat and mass transport in catalysis pellets. Particular emphasis has been directed to the determination of the isothermal effectiveness factor. Early studies have been compiled by Gonzo and Gottifredi (1982). These authors predicted the mentioned factor under non-isothermal conditions usually met in most chemical reactor design calculations, using a perturbation technique. More recently Villa (2000) presented a practical approach for a non classical numerical analysis of the solution of boundary value problems for high non-linear second order differential equations. These problems arise from energy and mass balance equations for non isothermal steady diffusion-reaction processes.
The class of described problems, leading to the solution of high non-linear second order differential equations, is the source of considerable theoretical and practical difficulties. It is the purpose of the present paper to demonstrate that an approach based on the power series method is a very effective tool for the solutions of the mentioned problems. The power series method is an old tool to solve ordinary differential equations. A wide open literature is available on this topic. In the last century several methods of finding exact and approximate solutions have been developed with the appearance of new problems in several disciplines. The finite-difference method and the variational methods have been extensively applied to solve problems in engineering. The finite element method gained an immense popularity among applied mathematicians and engineers. Nevertheless, the old technique of power series solutions has been ignored in the solutions of some boundary and/or eigenvalue problems which involve ordinary non-linear differential equations. Filipich et al. (2004), with a properly systematisation, applied it in various difficult problems. For instance, they succeeded in the application of this technique to strongly non-linear dynamical systems.
In the present paper, the potential usefulness of the largely ignored power series methods for solving non-linear ordinary differential equations which appear in the complex diffusion-reaction processes, is demonstrated. A simple, computationally efficient and very accurate analytical approach has been developed for the determination of the values of the nondimensional concentration u, the gradient u' and the effectiveness factor η, for different values of the characteristic parameters which correspond to relevant steady diffusion - reaction processes. The obtained algorithm is very general and it is attractive regarding its versatility in handling different values of the reaction order, the Thiele's modulus and other specific parameters.
Close agreement with results presented by previous investigators is demonstrated for several particular cases. Additionally, new numerical results were generated for several important cases, including those with experimental values for the parameters involved in the models of some industrial chemical reactions.
II. THEORETICAL CONCEPTS.
A. Introduction.
The process of diffusion-reaction in catalytic porous media is a matter of great interest in chemical reactor design. A great number of relevant cases are included in the following general boundary value problem:
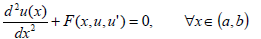 | (1) |
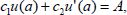 | (2) |
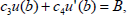 | (3) |
where ci where denotes the set of real number, i=1,2,...,4; a,b,A,B and the function F is continuous on [a,b]×(-∞,∞)×(-∞,∞).
The problem of existence and uniqueness of solution for initial value problems has extensively been investigated and a detailed analysis has been published. It is well known that in contrast the boundary value problems have several solutions or even no solution. This question has been analysed only for particular situations. So, the existence and uniqueness of the solution of the boundary value problem given by Eqs. (1)-(3) will be analysed, according to general theoretical results reported in the literature. For the sake of illustration, let us consider some known particular cases for which there exist more than one solution.
Example 1.
Consider the boundary value problem given by Eqs. (1)-(3) with F(u)=eu and a=0, b=1, c1=1, c2=0, c3=1, c4=0, A=B=0. In this case there exist two solutions (Bayley et al., 1968).
Example 2.
Consider the boundary value problem given by Eqs. (1)-(3) with 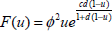 and a=0, b=1, c1=0, c2=1, c3=1, c4=0, A=0, B=1.
and a=0, b=1, c1=0, c2=1, c3=1, c4=0, A=0, B=1.
For the values
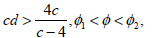 | (4) |
with 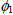 ,
,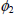 , three solutions exist. Outside the parametric region defined by (4) only one solution exists (Kubicek and Hlavacek, 1983).
, three solutions exist. Outside the parametric region defined by (4) only one solution exists (Kubicek and Hlavacek, 1983).
B. Analysis of a relevant steady diffusion - reaction process.
A very important steady diffusion-reaction process can be analysed when the boundary value problem given by Eqs. (1)-(3) is defined by
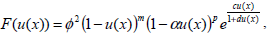 | (5) |
and
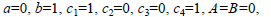 | (6) |
The function u in Eq. (5) is given by u=1-v, where v denotes a non-dimensional mass concentration of the key component referred to its surface value.
The physical interpretation of the parameters 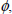 , m,α, p, c and d are given in Villa (2000).
, m,α, p, c and d are given in Villa (2000).
The following theorem, allows to analyse the existence and uniqueness of the corresponding solution (Bayley et al., 1968).
Theorem 1:
Let us consider the boundary value problem
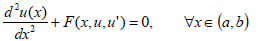 | (7) |
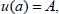 | (8) |
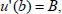 | (9) |
where the function F is continuous on [a,b] × (-∞,∞) × (-∞,∞) and satisfies the Lipschitz condition given as
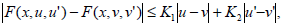 | (10) |
(u,v), (u',v')(-∞,∞)×(-∞,∞), where K1,K2, K1>0, K2≥0.
If b-a<g(K1,K2) with g(K1,K2) given by
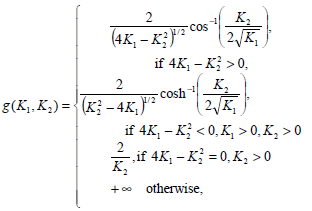 | (11) |
the boundary value problem given by Eqs. (7)-(9) has one and only one solution.
It is important to remark that from physical considerations the following restrictions hold on the parameters of the function F defined in Eq. (5):
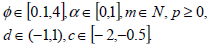 | (12) |
where N denotes the set of natural numbers.
The physical details are given in Gonzo and Gottifredi (1982). On the other hand the function F is nonnegative on the space [a,b]×(-∞,∞)×(-∞,∞), since it describes the kinetic law of the process. Then the application of the maximum principle leads to the following inequalities
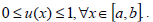 | (13) |
From (12), (13) and Theorem 1, the following inequality arises
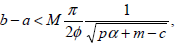 | (14) |
for any 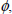 ,α,m and c defined by (12) and p≥1 or
,α,m and c defined by (12) and p≥1 or 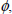 ,c,m and p defined by (12) and α=1.
,c,m and p defined by (12) and α=1.
It must be noted that in this case the Lipschitz constants K1 and K2, have the values K2=0 and
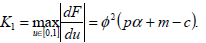 | (15) |
If the length b-a is fixed, the inequality (14) gives an additional restriction to the parameters involved in (12), which assure the existence and uniqueness of the solution. The Table 1 depicts values of the parameter M in some particular cases.
Table 1. Values of parameter M as a function of f,p,m,a and c. 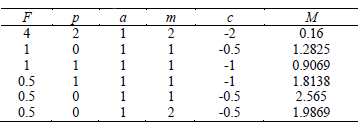
III. IMPLEMENTATION OF A TECHNIQUE BASED IN THE POWER SERIES METHOD.
The power series method involves the admission of sums of infinite power series as defining functions in the intervals were these series converge. The functions thus defined are called analytic. The fundamental as sumption in solving a differential equation is that the solution of this equation is in the form of a power series. This method constitutes a simple, computational efficient and accurate approach to solve the immense number of cases involved in the general boundary value problem given by Eqs. (1)-(3).
Consequently we consider a solution in the form
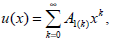 | (16) |
and assume that (16) converges |x|<R, where R denotes the convergence radius which determines an interval including [0,1]. The well known procedure of multiplication of power series means that if
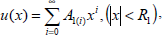
and
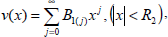
where R1 and R2 are positive, then
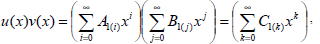 | (17) |
where
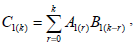 | (18) |
This series converges at least for |x|<min(R1,R2). In order to obtain u2(x) we write
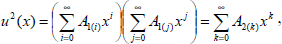
where
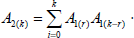
Applying mathematical induction, the power m of u(x) can be obtained as
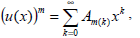 | (19) |
with
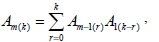 | (20) |
In the particular case where u(x)≡C, with C, it is convenient to write
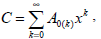 | (21) |
with A0(k)=Cδ0k where δ0k is the Kronecker delta. Within its domain of convergence every power series can be differentiated, term by term, any number of times. Hence if 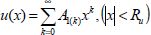 then the derivative u'(x) can be obtained using a term by term differentiation process
then the derivative u'(x) can be obtained using a term by term differentiation process 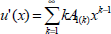 , with the same radius of convergence as the original series, i.e. convergent x, |x|<Ru. Consequently, the derivative of order n is given by
, with the same radius of convergence as the original series, i.e. convergent x, |x|<Ru. Consequently, the derivative of order n is given by
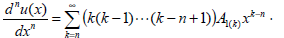 | (22) |
In order to collect the coefficients of like powers of x, we need to rewrite this series so that the general term is xk. Consequently, we make the substitution i=k-n. Thus we have
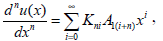 | (23) |
where
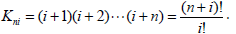 | (24) |
The series defined by Eq. (23) is convergent x, |x|<Ru. In the case of the differential equation
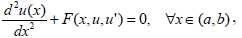 | (25) |
we assume a solution in the form (16). Differentiating twice we obtain
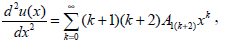 | (26) |
convergent x, |x|<Ru. We also assume that F(x,u(x),u'(x)) is analytic, i.e.
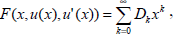 | (27) |
convergent x, |x|<RF.
Substituting Eqs. (26) and (27) into Eq. (25) and collecting the terms involving like powers of x, we obtain the recurrence formula which allows the determination of coefficients A1(k+2), k=0, 1, 2, ... .
When the function F(x,u(x),u'(x)) is given by
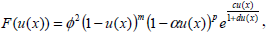 | (28) |
we assume
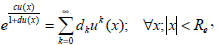 | (29) |
where the dk are the Taylor coefficients of the function 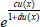 .
.
The term (1-u(x))m is obtained by well known binomial formula
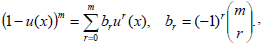 | (30) |
From Eqs. (19) and (20) we have
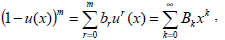 | (31) |
where 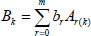 , and the series is convergent |x|<Ru. Similarly, applying Eq. (19) in the binomial formula
, and the series is convergent |x|<Ru. Similarly, applying Eq. (19) in the binomial formula 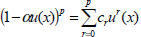 , where
, where 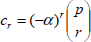 leads to
leads to
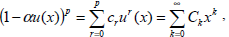 | (32) |
where 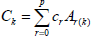 , and the series is convergent |x|<Ru.
, and the series is convergent |x|<Ru.
The product (1-u(x))m (1-αu(x))p is obtained applying Eqs. (17) and (18) and is given by
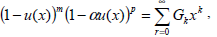 | (33) |
where 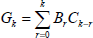 , and the series is convergent |x|<Ru. Taking into account Eqs. (19) and (29) the expression of
, and the series is convergent |x|<Ru. Taking into account Eqs. (19) and (29) the expression of 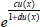 can be written as
can be written as
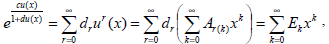 | (34) |
where 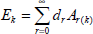 , and the series is convergent |x|<Ru.
, and the series is convergent |x|<Ru.
Applying Eqs. (33) and (34) the expression of F(u(x)) can be written as
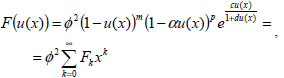 | (35) |
where 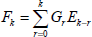 . The series in Eq. (35) is convergent x, |x|<min(Ru,Re).
. The series in Eq. (35) is convergent x, |x|<min(Ru,Re).
Substituting Eqs. (26) and (35) into Eq. (25) leads to
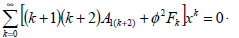 | (36) |
In consequence the recurrence formula is given by
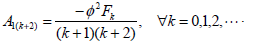 | (37) |
From (16) it must be noted that the coefficients to be determined are given by
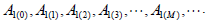 | (38) |
but the recurrence formula (37) yields
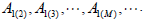 | (39) |
Consequently, in this case, the power series method produces two arbitrary coefficients A1(0) and A1(1).
Let us consider the boundary value problem (7)-(9) with a=0, b=1, A=B=0,
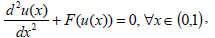 | (40) |
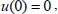 | (41) |
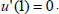 | (42) |
From the boundary condition (41) there follows A1(0)=0. On the other hand, the boundary condition (42) leads to
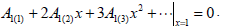 | (43) |
Finally, the coefficient A1(1) can be obtained by the well known shooting method (Gottifredi et al., 1981b; and Kubicek and Hlavacek, 1983).
It must be noted that the application of the power series method to the boundary value (40)-(42) implies the convergence of the different power series involved in all the interval [0,1]. If this is not the case, for instance, if Ru>1, in general it is sufficient if the interval [0,1] is partitioned in N subintervals and the method is applied over each subinterval.
IV. NUMERICAL RESULTS.
In order to establish the validity, accuracy and applicability of the developed algorithm, numerical results were computed for a number of cases, which correspond to the boundary value problem given by Eqs. (7)-(9), and which were available in the literature. Additionally, new numerical results were generated for several important problems.
Table 2 shows values of the nondimensional concentration u and gradient u' for different values of the reaction order m, the Thiele's modulus 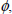 and A=B=0. Table 3 depicts values of the effectiveness factor η, for different values of the reaction order m, the Thiele's modulus
and A=B=0. Table 3 depicts values of the effectiveness factor η, for different values of the reaction order m, the Thiele's modulus 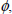 and the thermicity d and the parameter
and the thermicity d and the parameter 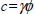 where γ denotes the Arrhenius number.
where γ denotes the Arrhenius number.
Table 2. Non-dimensional concentration u(x) and u'(x) in the pellets, p=0, a=1, c=-0.5, d=-0.1, 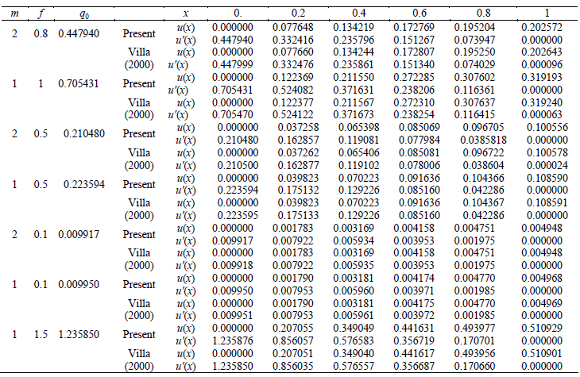
Table 3. Effectiveness factor h (p=0). 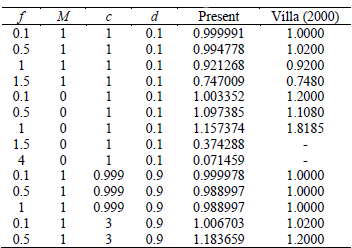
Tables 2 and 3 show a comparison of values with those of Villa (2000). This comparison shows a very close agreement in almost all cases. In Villa (2000) a practical complement to classical perturbation and numerical techniques for use in the analysis of steady diffusion-reaction process is presented. This approach combines basic aspects from elementary functional analysis, integral equations and differential calculus.
Table 4 depicts values of the effectiveness factor η, for different values of the reaction order m, the Thiele's modulus f and the parameters c and d. A comparison with Gonzo and Gottifredi (1982) and Villa (2000) is included. In Gonzo and Gottifredi (1982) a technique to estimate the non-isothermal effectiveness factor η is presented. This approach is based on the matching analysis for the asymptotic case for the Thiele's modulus 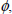 . This development is an extension of a previously developed technique (Gottifredi et al.,1981a,b).
. This development is an extension of a previously developed technique (Gottifredi et al.,1981a,b).
Table 4. Effectiveness factor h (p=0). 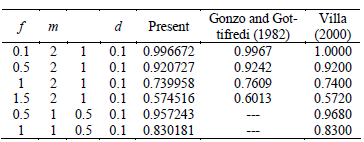
Table 5 depicts values of the effectiveness factor η, for different values of the Thiele's modulus 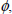 , and the parameters c and d. These parameters correspond to experimental values of some industrial chemical reactions, Muñoz Tavera (2005). Finally, Table 6 depicts new values of the nondimensional concentration u and gradient u' for the same set of parameters defined in Table 5.
, and the parameters c and d. These parameters correspond to experimental values of some industrial chemical reactions, Muñoz Tavera (2005). Finally, Table 6 depicts new values of the nondimensional concentration u and gradient u' for the same set of parameters defined in Table 5.
Table 5. Effectiveness factor h (p=0) (1): Synthesis of vinylchloride. (2): Oxidation of CH3OH to CH2O (3): NH3 synthesis. (4): Oxidation of ethylene. 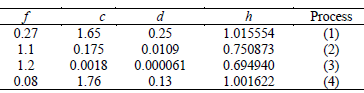
Table 6. Non-dimensional concentration u(x) and gradient u'(x) in the pellets, p=0, m=1, a=1. 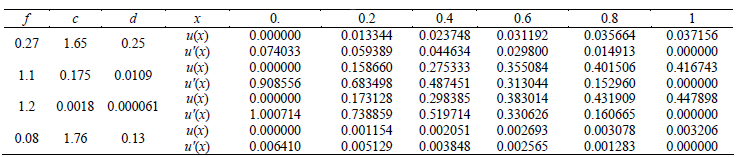
5. CONCLUSIONS.
The potential usefulness of a technique based on the power series methods for solving non-linear ordinary differential equations, which appear in the complex diffusion-reaction processes, has been demonstrated.
Numerical results were computed for a number of cases which correspond to boundary value problems available in the literature. Additionally, new numerical results were generated for several important practical cases.
ACKNOWLEDGMENTS
The authors are grateful to Drs. Juan Carlos Gottifredi and Elio E. Gonzo for their valuable comments and suggestions. The present investigation has been sponsored by CONICET Research and Development Program (PIP 5340) and CIUNSA.
REFERENCES
1. Bayley, P.B., L.F. Shampine and P.E. Waltman, Non-linear Two Point Boundary Value Problems, Academic Press, New York (1968). [ Links ]
2. Filipich, C.P., M.B. Rosales and F. Buezas, "Some non-linear mechanical problems solved with analytical solutions," Latin American Applied Res., 34, 101-109 (2004). [ Links ]
3. Gonzo, E. and J.C. Gottifredi, "Non isothermal effectiveness factor estimation with simple analytical expressions," Lat. Am. J. Heat Mass Transf., 6, 113-129 (1982). [ Links ]
4. Gottifredi, J.C, E.E. Gonzo and O.D. Quiroga, "Isothermal effectiveness factor I. Analytical expression for single reaction with arbitrary kinetics. Slab geometry," Chem. Eng. Sci., 36, 705-711 (1981a). [ Links ]
5. Gottifredi, J.C, E.E. Gonzo and O.D. Quiroga, "Isothermal effectiveness factor II. Analytical expression for single reaction with arbitrary kinetics, geometry and activity distribution," Chem. Eng. Sci., 36, 713-719 (1981b). [ Links ]
6. Kubicek, M. and V. Hlavacek, Numerical Solution of Non-linear Boundary Value Problems with Applications, Prentice Hall, Inc, Englewood Cliffs New Jersey (1983). [ Links ]
7. Muñoz Tavera, E., "Analytical expression for the non-isothermal effectiveness factor: the nth-order reaction in a slab geometry," Chem. Eng. Sci., 60, 907-916 (2005). [ Links ]
8. Villa L.T, "A mathematical approach to analyse a steady diffusion-reaction process," Latin Amercan Applied Res., 30, 1-8 (2000). [ Links ]
Received: April 28, 2008
Accepted: June 30, 2009
Recommended by Subject Editor: Orlando Alfano.














