Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. vol.40 no.4 Bahía Blanca oct. 2010
A biphasic hyperelastic model for hydrocephalus
J. J. García† and J. H. Smith‡
† Escuela de Ingeniería Civil y Geomática, Universidad del Valle, Cali, Colombia
josejgar@gmail.com
‡ Department of Mechanical Engineering, Lafayette College, Easton, PA 18042, USA
smithjh@lafayette.edu
Abstract — A biphasic hyperelastic model with spherical symmetry is presented to study hydrocephalus. The model can take into account the biphasic nature of brain tissue, non-linear stress-strain curves through an Ogden-type compressible strain energy function, a nonlinear variation of hydraulic conductivity with deformation, a constant production of cerebrospinal fluid (CSF) as well as a fluid absorption rate proportional to pressure. The biphasic equations were implemented in an updated Lagrangian finite element code where a novel procedure was devised to consider the constant generation of CSF in the ventricles. Results of a non-communicating model showed strains in the range of 35-45% in the peri-ventricular area and pore pressure and radial displacement distributions that were not significantly affected by material nonlinearities. High circumferential stresses documented in acute hydrocephalus suggest that the tissue may suffer damage at the ventricular surface while a communicating model was not capable of reproducing normal pressure hydrocephalus. Overall results suggest that normal pressure hydrocephalus cannot be explained with models that consider an elastic law for the solid phase of the material.
Keywords — Acute Hydrocephalus; Normal Pressure Hydrocephalus; Porohyperelastic Model; Hyperelastic Biphasic Model.
I. INTRODUCTION
The cerebrospinal fluid (CSF) present in the central nervous system plays an important role in the physiological activities and protection of the brain. This fluid is produced at a constant rate in the choroid plexuses of the lateral and third ventricles and flows within the Sylvius aqueduct to the fourth ventricle, whence it goes through small passages to the subarachnoid space. Disruptions of the CSF flow lead to different forms of a disease known as hydrocephalus, characterized by a significant increment of the ventricular space. In acute hydrocephalus the Sylvius aqueduct is blocked and ventricular pressure is greatly increased. In contrast, normal pressure hydrocephalus (NPH) is characterized by a significant deformation of the ventricles without an increase of the transmantle pressure or evidence of aqueduct blockage. It is important to study the biomechanics of hydrocephalus in order to help understanding the etiology of the disease, which may lead to better treatments or the development of more precise diagnostic tools.
In addition to several studies aimed to understand problems associated with the deformation of the brain (Wittek et al., 2007), many mechanical models have been proposed to analyze hydrocephalus. Some of these models have considered brain tissue as a single phase elastic or viscoelastic material (Sivaloganathan et al., 2005; Drapaca et al., 2006). Beginning with the work of Nagashima et al. (1987), other models have simulated brain tissue as a poroelastic material, including the work of Kaczmarek et al. (1997) for a cylindrical geometry, of Taylor and Miller (2004) for a planar geometry, and of Smillie et al. (2005) and Sobey and Wirth (2006) for a spherical symmetric geometry.
All these models have generally given good correlations of clinical observations for acute hydrocephalus, however they have not considered the nonlinear stress-strain response that has been experimentally documented for brain tissue under finite deformations (Miller, 1999; Franceschini et al., 2006). Considering that displacements occurring during acute hydrocephalus can be significantly large, it would appear that nonlinear stress-strain curves under finite deformations should be taken into account, as recently proposed by Dutta-Roy et al. (2008) in a patient-specific non-communicating model that was unable to explain NPH. Whereas this model represents an important advance from the geometric point-of-view, it includes a pressure gradient condition not consistent with the constant generation of CSF and does not include the effect of CSF flow from the ventricles to the subarachnoid space through the Sylvius aqueduct.
While a physical explanation for acute hydrocephalus seems to be well agreed upon, many attempts have been made to explain NPH. The primary issue is that a communicating (unblocked) aqueduct minimizes the secondary mechanism of flow of CSF to the subarachnoid space through the parenchyma. Recent analysis by Levine (1999) and Sobey and Wirth (2006) suggest that large displacements in NPH can be explained by a combination of fluid absorption in the parenchyma and small values of hydraulic conductivity, however these models did not consider nonlinear stress-strain response of brain tissue.
A mechanical model intended to explain both communicating and non-communicating hydrocephalus is presented here that can take into account the biphasic nature of brain tissue and non-linear stress-strain curves under finite deformations using a hyperelastic function valid for compressible materials. The model also allows simulating the constant generation of CSF and it includes a strain-dependent hydraulic conductivity as well as transvascular fluid absorption in the whole parenchyma. We first analyze the case of acute hydrocephalus caused by a blockage of the aqueduct, and then we conduct analyses of communicating models to determine if the rise in the fluid pressure and the displacement of the ventricles are consistent with the pathology of NPH.
II. METHODS
The spherical model for brain recently used by Smillie et al. (2005) and Sobey and Wirth (2006) was adopted in this analysis (Fig. 1). Brain tissue was assumed to be represented by a spherical domain of inner radius 30 mm and outer radius 100 mm, where the interface between the white matter (toward the ventricles) and gray matter (toward the subarachnoid space) was assumed to be a spherical surface of radius 70 mm. The ventricles were represented by the inner sphere of radius 30 mm and the brain parenchyma was assumed to be fully saturated with CSF.
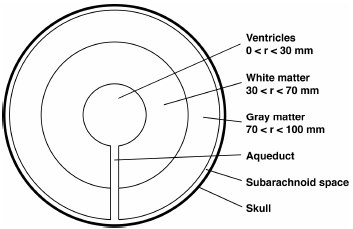
Figure 1. Schematic diagram of a spherically symmetric model of the brain, showing the ventricles, gray and white matter, subarachnoid space, skull, and the Sylvius aqueduct connecting the ventricles and subarachnoid space with negligible thickness.
Fluid flow and finite deformations in a hydrated biological tissue considering spherical symmetry are described by the following equations:
 | (1) |
 | (2) |
The variables σr and σθ are the effective stresses in radial and tangential direction, respectively, vs is the velocity of the solid phase, p is the pore pressure, the coefficient κ is the hydraulic conductivity, and k is the coefficient of fluid absorption. All functions only change with the radial Eulerian coordinate r. Equation (1) is a statement of force equilibrium and Eq. (2) is a statement of fluid mass continuity, incorporating Darcy's law and fluid absorption dependent on the pressure, consistent with Levine (1999). A well known nonlinear updated finite element Lagrangian scheme (Belytschko et al., 2000) was used to implement these equations, where the validation of the code was accomplished comparing numerical results with closed-form solutions reported in the literature (García and Cortés, 2006).
Since the strain rates associated with the development of hydrocephalus are so slow, the intrinsic viscous effects of the solid phase were neglected. Thus, the solid phase was represented by a hyperelastic isotropic function W (Ogden, 1984) as follows:
 | (3) |
where λr and λθ are, respectively, the radial and circumferential stretch ratios,μk,αk, and μ' are material parameters, and J is the determinant of the deformation gradient tensor. The material parameters can be adjusted to yield the Young's modulus E and Poisson 's ratio ν at zero strain as follows
 | (4) |
 | (5) |
This energy function allows reproducing the nonlinear behavior of brain tissue under finite deformations, as shown by Miller and Chinzei (2002) and Franceschini et al. (2006). The parameters αk can be adjusted to describe the shape of stress-strain curves. Therefore, to assess the sensitivity of results with respect to material nonlinearities, two sets of parameters were used in this study. Based on the experimental study of Miller and Chinzei (2002), in the first set only one term was considered with α1=-4.7. In addition, based on the experimental study of Franceschini et al. (2006), in the second set two terms were considered with α1=4.31 and α2=7.74. To be consistent with other studies of hydrocephalus (Taylor and Miller, 2004), a Young's modulus E of 584 Pa and a Poisson's ratio ν of 0.35 were used in this study. Based on these values the parameters μk and μ' for each set were calculated using Eqs. (4) and (5).
The variation of hydraulic conductivity with strain was assumed to depend on tissue dilatation as follows:
 | (6) |
where κ0 is the hydraulic conductivity at zero strain, M is a nondimensional parameter that controls the variation of hydraulic conductivity, and e is the volume dilatation, that can be related to the radial (λr ) and circumferential (λθ) stretch ratios as
 | (7) |
Consistent with other models (Smillie et al., 2005; Sobey and Wirth, 2006), a uniform value of κ0 equal to 15.7 mm4 / (N.s) was assumed for the whole parenchyma, or a value of 15.7 mm4 / (N.s) was assumed for
Table 1. Summary of material parameters used in this study
the white matter and of 4 mm4 / (N.s) for the gray matter (Cheng and Bilston, 2007). The parameter M was set equal to 4.3 (Kaczmarek et al., 1997; Sobey and Wirth, 2006) and the absorption coefficient was varied between 0 and 3 mm2 / (N.s) to cover a wide spectrum of properties. This represents a relatively high value of absorption considering that the square root of the relation between hydraulic conductivity and absorption is equal 2.29 mm, which is the distance that fluid can permeate the parenchyma before being attenuated one natural logarithmic unit (Levine, 1999). A summary of material parameters is presented in Table 1.
We adopt the conditions at the inner boundary proposed by Smillie et al. (2005) as follows. A constant production of CSF of 5.8 mm3/s was assumed, consistent with the experimental findings of Cutler et al. (1968) and Ekstedt (1978). As proposed by Smillie et al. (2005), the fluid flow through the aqueduct, Qa, was assumed to be described by Poiseuille equation as
 | (8) |
where d and L are the diameter and length of the aqueduct, respectively, μ is the viscosity of the fluid and Δp is the pore pressure difference between the ventricles and the subarachnoid space. To model the aqueduct in our finite element code, an element was created connecting the inner and outer nodes, with an effective hydraulic conductivity coefficient kef calculated from the following equation
 | (9) |
where Δ r is the difference of radius between the outer and inner spheres (70 mm) and r is the average radius. In order to simulate non-communicating hydrocephalus and partial obstructions of the aqueduct, this effective hydraulic conductivity was varied according to Eq. (9).
Since the amount of CSF generated inside the ventricles was assumed to be constant and the inner sphere may have significant radial displacements, fluid velocity and internal pressure are dependent on deformation, which are conditions difficult to implement numerically.
To circumvent this problem, an artificial inner fixed boundary was created in which fluid flow was defined, thus guaranteeing constant CSF generation. The connection between this artificial sphere and the inner sphere of radius 30 mm was made with an element with elastic properties 10-5 lower than those of the brain and with a hydraulic conductivity 105 higher than that of the parenchyma. Hence, the inner sphere of 30 mm initial radius was then able to displace in order to satisfy the governing equations at each time step. Analyses showed that the radius of the artificial sphere did not affect the results, hence, this sphere was assumed to be of 29 mm of radius.
The absorption of CSF at the subarachnoid space is dependent on the pressure differential with the venous system. However, Smillie et al. (2005) showed that the pressure in the subarachnoid space is approximately equal to blood pressure. Hence, a prescribed null pressure was considered for the outer boundary, which means that pore pressure distributions obtained in these analyses are relative to the pressure in the subarachnoid space. Additionally, consistent with other studies of hydrocephalus (Smillie et al., 2005; Sobey and Wirth, 2006), we assumed that the subarachnoid space has a negligible thickness and that the skull is greatly stiffer than brain tissue. Thus, we have included a fixed condition at the outer boundary.
With the combination of material parameters described above, analyses were conducted for both communicating and non-communicating hydrocephalus as well as partial blockage of the aqueduct. The aspect ratio (Hakim et al., 1976) calculated as the quotient between the outer and the inner radius in the deformed geometry was used to quantify hydrocephalus conditions, where an aspect ratio near 2 (or smaller) indicated hydrocephalus in an adult patient.
II. RESULTS
The energy function allowed obtaining stress-strain curves similar to those of the incompressible function (Fig. 2). The nonlinear parameters from Franceschini et al. (2006) yielded a stiffening effect more marked in tension, while the nonlinear parameter from Miller and Chinzei (2002) predicted a stiffening effect only in compression, with softening in tension.

Figure 2. Uniaxial stress response for the two sets of nonlinear parameters: α1 = -4.7, α2 = 0 from Miller and Chinzei (2002) and α1 = 4.31, α2 = 7.74 from Franceschini et al. (2006). The Young's modulus of 580 Pa is equal to the slope of each curve at zero deformation, i.e., stretch ratio equal to one.
For the non-communicating model (blocked aqueduct) and the two sets of nonlinear parameters, similar curves were obtained for the pore pressure, radial displacement and circumferential stretch distributions with maximum differences of 12.9%, 22.8%, and 5.9% for the maximum values, respectively (Fig. 3a-3c). In contrast, important differences were observed in the maximum values of circumferential stress displaying a maximum difference of 170% (Fig. 3d). Strains larger than 10% were present at the peri-ventricular area in a volume corresponding to approximately 23% of the total volume. The consideration of a hydraulic conductivity coefficient dependent on strain caused a reduction of the maximum pore pressure, pore pressure slope, radial displacement, and fluid fraction at the ventricular surface (Fig. 4). The inclusion of absorption caused reductions of 65%, 55% and 30%, respectively, for the maximum values of pore pressure, radial displacements, and fluid fraction (Fig. 5). With the aspects ratios were in the range 2.3-2.5 and the inclusion of absorption incremented this range to 2.8-2.9.

a. Pore pressure

b. Radial displacement

c. Distance from deformed ventricles (mm)

d. Circumfential stress.
Figure 3. Pore pressure, radial displacement, circumferential stretch, and circumferential stress distributions for the non-commnunicating model for the two sets of nonlinear parameters with constant hydraulic conductivity (κ0 = 15.7 mm 4 / (N.s) and M = 0) and zero fluid absorption (k = 0). Note that distributions are shown relative to the distance from the deformed ventricle surface. The amount that the ventricle displaced is the radial displacement value for a distance of zero.

a. Pore pressure

b. Radial displacement

c. Fluid fraction
Figure 4. Pore pressure, radial displacement, and fluid fraction distributions for the non-commnunicating model for the nonlinear parameter set with α1 = -4.7 and α2 = 0 considering the variation of hydraulic conductivity with deformation (κ 0 = 15.7 mm4 / (N.s) and M = 0 or M = 4.3) and zero fluid absorption (k = 0).

a. Pore pressure

b. Radial displacement

c. Fluid fraction
Figure 5. Pore pressure, radial displacement, and fluid fraction distributions for the non-commnunicating model for the nonlinear parameter set with α1 = -4.7 and α2 = 0 considering the variation of hydraulic conductivity with deformation (κ 0 = 15.7 mm4 / (N.s) and M = 0 or M = 4.3) and fluid absorption (k = 0 or k = 3 mm2 / (N.S)).
The use of non-homogeneous values for the hydraulic conductivity yielded an almost twofold increment of the ventricular pressure as well as qualitative changes in all distributions (Fig. 6). Mostly, in the non-homogeneous model the slopes of the curves were higher in the gray matter and the fluid fraction became equal to zero near the outer boundary.

a. Pore pressure

b. Radial displacement

c. Fluid fraction
Figure 6. Pore pressure, radial displacement, and fluid fraction distributions for the non-commnunicating model for the nonlinear parameter set with α1=-4.7 and α2=0 considering the variation of hydraulic conductivity with deformation (Homogeneous: κ 0=15.7 mm4 / (N.s) for both gray and white matter; Nonhomogeneous: κ 0= 4.0 mm4 / (N.s) for the inner gray matter and κ 0=15.7 mm4 / (N.s) for the outer while matter; Both: M = 4.3) and zero fluid absorption (k = 0).
All analyses with the communicating model (open aqueduct) yielded an aspect ratio virtually equal to the initial aspect ratio, i.e. 3.33, indicating that this model could not predict NPH. In addition, maximum radial displacements were low (0.0016 mm) and therefore, results did not depend on the nonlinear elastic properties. Hence, the following results were obtained with the nonlinear parameter set with α1 = -4.7 and α2 = 0. A maximum ventricular pressure of 0.54 Pa was obtained for all combinations of material parameters. In addition, all distributions were independent of the permeability coefficients (Fig. 7). The increase of the absorption coefficient caused an increment of the pressure slope and a small increment (14%) of the maximum displacement (Fig. 8). Considering the communicating model and all combination of material parameters, the maximum percentage of flow through the parenchyma was only 0.028%, obtained with the maximum permeability and maximum fluid absorption coefficient, while a tenfold decrease in permeability reduced this percentage of flow to 0.0024 %.

a. Pore pressure

b. Radial displacement
Figure 7. Pore pressure and radial displacement distributions for the communicating model for the nonlinear parameter set with α1=-4.7 and α2=0 considering the variation of hydraulic conductivity with deformation (κ0 = 0.157 mm4 / (N.s) or κ0 = 15.7 mm4 / (N.s) and M = 0 or M = 4.3) and zero fluid absorption (k = 0). No significant differences were observed in the distributions.

a. Pore pressure

b. Radial displacement
Figure 8. Pore pressure and radial displacement distributions for the communicating model for the nonlinear parameter set with α1 = -4.7 and α2 = 0 considering the variation of fluid absorption (k = 0, 0.3, or 3.0 mm 2 / (N.s))
Considering a partially closed aqueduct and all the other analyses, there was an approximately exponential relation between ventricular pressure and radial displacement, as depicted by the approximately linear relationship between the data plotted using a logarithmic scale (Fig. 9).

Figure 9. Ventricular pressure and radial displacement of the ventricular wall for the communicating and non-communicating models considering all combinations of material parameters analyzed in this study. The approximately linear relationship for the communicating model on the logarithmic scale indicates an exponential relationship between these quantities.
IV. DISCUSSION
A biphasic hyperelastic model was proposed for hydrocephalus that includes fluid absorption, a hydraulic conductivity dependent on strain, and a boundary condition consistent with the constant generation of CSF. Different from other models that have used Hooke's law for the solid phase, this approach includes an Ogden-type compressible function similar to that has been successfully used to fit experimental stress-strain curves of brain tissue under finite deformations (Miller and Chinzei, 2002; Franceschini et al., 2006). The function used here allows considering a compressible response for the solid phase, which gives a better representation of the behavior of the tissue (Tenti et al., 2000) and provides a higher degree of versatility to undertake parametric studies. It also allows the description of elastic nonlinearities that are deemed to be present for the high strain fields of acute hydrocephalus.
Comparison of results obtained with the non-communicating model (blocked aqueduct) and the two sets of nonlinear parameters indicate that ventricular pressure, radial displacement, and circumferential stretch are not highly sensitive to material nonlinearities. This may be explained since these functions are most affected by the global behavior of the tissue, which is subjected to strains lower than 10% in approximately 80% of the volume. On the other hand, large local strains (~40%) attained at the ventricular surface induce important differences in the circumferential stress, that, according to the nonlinear stress-strain curves for the two sets of nonlinear parameters, has important variations for strains near 30% (Fig. 2). Stress concentration at the ventricle surface may be even higher considering the geometric irregularities of real ventricles compared to the idealized sphere of this analysis. This result supports the hypothesis that the tissue may experience some local damage or "bioplastic yielding" during acute hydrocephalus (Hakim et al., 1976).
For the non-communicating model, ventricular pressure and radial displacement are within the range documented in other studies. For instance, comparison of our results for the parameter set with a1 = -4.7 and those by Sobey and Wirth (2006) using the Hooke's law indicates similar transmantle pressure (~400 Pa) and similar shapes of the radial displacement and pore pressure curves, as well as reduced maximum values of radial displacement, pore pressure and fluid content for the nonlinear permeability analyses compared to the results from the constant permeability models (Fig. 4). Additionally, the radial displacement from our analysis of approximately 11 mm is similar to 10 mm reported by Sobey and Wirth (2006). The range of aspect ratios(2.3-2.4) obtained with the non-communicating model is higher than the threshold of 2.0 that has been deemed to be an indicator of hydrocephalus in an adult patient (Hakim et al., 1976). However, considering than radial displacements are highly sensitive to permeability, aspect ratios closer to 2.0 may be obtained with a hydraulic conductivity lower than that used in our analyses that was chosen to be consistent with other studies of hydrocephalus. Increments of fluid content in the peri-ventricular area are also in agreement with previous analytical studies and with experiments on dogs (Kaczmarek et al., 1997). This can be explained considering the increments of circumferential strain near the ventricular space.
Given the low displacements attained with the communicating models (open aqueduct), results were the same for the two sets of nonlinear parameters since each of them yields the same slope of the stress-strain curve under infinitesimal deformations. Moreover, results did not depend on the nonlinear variation of hydraulic conductivity which in this case remained approximately uniform since the fluid fraction was constant throughout the whole domain. The independence of the ventricular pressure with material parameters can be explained since the aqueduct is opened and it establishes the pressure difference between the ventricle and the subarachnoid space. The analyses with a partially obstructed aqueduct showing increases of ventricular displacement with increments of ventricular pressure are consistent with the increment of resistance through the aqueduct.
For the communicating model, the small increment of radial displacement and the slope of the pore pressure curve with the increase of the fluid absorption coefficient is consistent with results by Sobey and Wirth (2006) but it is not enough to explain NPH because the aspect ratio from all analyses was virtually the same of normal conditions. Since the aqueduct is open, only a small amount of CSF flows through the interstitial spaces, either to be absorbed within the peri-ventricular area or to traverse the whole parenchyma to the subarachnoid space. Therefore, the drag of this small amount of flow cannot cause significant displacement of the parenchyma. These results are in conflict with those of Levine (1999) and Sobey and Wirth (2006), who suggested that NPH can be explained considering combinations of high fluid absorption and reduced hydraulic conductivity coefficients. The reason for this disagreement appears to be that Sobey and Wirth (2006) set a priori the percentage of flow to traverse the parenchyma (approximately 17-30%), while the analyses presented here showed that this percentage is negligible (0.028%) and therefore cannot alter displacement and pressure fields which are essentially the same as those of the normal conditions. Additional analyses (not shown) considering combinations of high fluid absorption and increased hydraulic conductivity coefficients also did not result in significant displacements of the ventricles.
Considering all sets of material parameters, the strong relation between pressure and ventricular enlargement suggests that significant displacements cannot be obtained with a low ventricular pressure using elastic models. Therefore it would appear that NPH cannot be explained with models such as this that consider the solid phase as an elastic material, a similar conclusion to that recently suggested by Dutta-Roy et al. (2008). The most feasible explanation for this behavior is that the deformations of the elastic skeleton depend on the applied load, which is produced by the dragging force of the fluid traveling through the interstitial spaces. In a communicating model, due to the low resistance through the aqueduct, only a small amount of fluid traverses the poroelastic skeleton. Thus, it cannot generate the required force to produce a significant enlargement of the ventricles.
One possible explanation for the onset of NPH is that during a temporary blockage of the aqueduct, the high peak stress in the peri-ventricular area may cause damage or "bioplastic yielding" (Hakim et al., 1976), which cannot be recovered when the aqueduct is reopened. To be able to simulate this condition, a damage theory has to be incorporated in this model. However, the experimental assessment of this hypothesis would require a complete history of ventricular pressure and enlargement, which is difficult to acquire in clinical practice considering the invasive nature of pressure measurements.
Limitations of the model include the consideration of a spherical symmetric configuration. Thus, efforts have to be made to describe patient specific geometries, as has been recently presented by Dutta-Roy et al. (2008). Elastic properties used here were adjusted from those documented in the literature, however, more experimental work has to be done to determine material parameters (e.g., Poisson's ratio) and their spatial distribution in order to obtain more accurate predictions.
REFERENCES
1. Belytschko, T., W.K. Liu and B. Mora, Nonlinear finite elements for continua and structures, John Wiley & Sons, Chichester (2000). [ Links ]
2. Bruehlmeier, M., U. Roelcke, P. Bläuenstein, J. Missimer, P.A. Schubiger, J.T. Locher, R. Pellikka and S.M. Ametamey, "Measurement of the extracellular space in brain tumors using 76Br-bromide and PET," Journal of Nuclear Medicine, 44, 1210-1218 (2003). [ Links ]
3. Cheng, S. and L. Bilston, "Unconfined compression of white matter," Journal of Biomechanics, 40, 117-124 (2007). [ Links ]
4. Cutler, R.W.P., L. Page, J. Galicich and G.V. Watters, "Formation and absorption of cerebrospinal fluid in man," Brain, 91, 707-720 (1968). [ Links ]
5. Dutta-Roy, T., A. Wittek and K. Miller, "Biomechanical modelling of normal pressure hydrocephalus," Journal of Biomechanics, 41, 2263-2271 (2008). [ Links ]
6. Drapaca, C.S., G. Tenti, K. Rohlf and S. Sivaloganathan, "A quasi-linear viscoelastic constitutive equation for the brain: application to hydrocephalus," Journal of Elasticity, 85, 65-83 (2006). [ Links ]
7. Ekstedt, J., "CSF hydrodynamic studies in man. 2. Normal hydrodynamic variables related to CSF pressure and flow," Journal of Neurology, Neurosurgery, and Psychiatry, 41, 345-353 (1978). [ Links ]
8. Franceschini, G., D. Bigoni, P. Regitnig and G.A. Holzapfel, "Brain tissue deforms similarly to filled elastomers and follows consolidation theory," Journal of the Mechanics and Physics of Solids, 54, 2592-2620 (2006). [ Links ]
9. García, J.J. and D.H. Cortés, "Modelo bifásico no lineal de elementos finitos para el análisis mecánico de tejidos biológicos. Parte II Implementación numérica y validación," Ingeniería & Desarrollo, 19, 57-73 (2006). [ Links ]
10. Hakim, S., J.G. Venegas and J.D. Burton, "The physics of the cranial cavity, hydrocephalus and normal pressure hydrocephalus: mechanical interpretation and mathematical model," Surgical Neurology, 5, 187-210 (1976). [ Links ]
11. Kaczmarek, M., R.P. Subramaniam and S.R. Neff, "The hydromechanics of hydrocephalus: steady-state solutions for cylindrical geometry," Bulletin of Mathematical Biology, 59, 295-323 (1997). [ Links ]
12. Levine, D.N., "The pathogenesis of normal pressure hydrocephalus: a theoretical analysis," Bulletin of Mathematical Biology, 61, 875-916 (1999). [ Links ]
13. Miller, K., "Constitutive model of brain tissue suitable for finite element analysis of surgical procedures," Journal of Biomechanics, 32, 531-537 (1999). [ Links ]
14. Miller, K. and K. Chinzei, "Mechanical properties of brain tissue in tension," Journal of Biomechanics, 35, 483-490 (2002). [ Links ]
15. Nagashima, T., N. Tamaki, S. Matsumoto, B. Horwitz and Y. Seguchi, "Biomechanics of hydrocephalus: a new theoretical model," Neurosurgery, 21, 898-904 (1987). [ Links ]
16. Ogden, R.W., Non-Linear Elastic Deformations. Dover Publications, Mineola, NY (1984). [ Links ]
17. Sivaloganathan, S., M. Stastna, G. Tenti and J.M. Drake, "A viscoelastic approach to the modelling of hydrocephalus," Applied Mathematics and Computation, 163, 1097-1107 (2005). [ Links ]
18. Smillie, A., I. Sobey and Z. Molnar, "A hydrostatic model of hydrocephalus," Journal of Fluid Mechanics, 539, 417-443 (2005). [ Links ]
19. Sobey, I. and B. Wirth, "Effect of non-linear permeability in a spherically symmetric model of hydrocephalus," Mathematical Medicine and Biology, 23, 339-361 (2006). [ Links ]
20. Tenti, G., J.M. Drake and S. Sivaloganathan, "Brain biomechanics: mathematical modeling of hydrocephalus," Neurological Research, 22, 19-24 (2000). [ Links ]
21. Taylor, Z. and K. Miller, "Reassessment of brain elasticity for analysis of biomechanisms of hydrocephalus", Journal of Biomechanics, 37, 2592-2620 (2004). [ Links ]
22. Wittek, A., K. Miller, R. Kikinis and S.K. Warfield, "Patient-specific model of brain deformation: Application to medical image registration," Journal of Biomechanics, 40, 919-929 (2007). [ Links ]
Received: December 8, 2008.
Accepted: September 24, 2009.
Recommended by Subject Editor: Alberto Cuitiño.














