Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. vol.40 no.4 Bahía Blanca oct. 2010
Modeling water absorption of sorghum during soaking
M. Kashiri, M. Kashaninejad and N. Aghajani
Department of Food Science & Technology, Gorgan University of Agricultural Sciences and Natural Resources, Beheshti Ave., Gorgan,49138-15739, Iran
kashaninejad@yahoo.com, kashani@gau.ac.ir
Abstract — Water absorption of sorghum during soaking in water at temperatures of 10, 20, 30, 40 and 50 ºC was simulated using Peleg's model. The weight gain during soaking process was determined in terms of moisture content. Peleg's equation was adequately capable to predict water uptake of sorghum under the experimental conditions. The Peleg rate constant, k1, and capacity constant, k2, decreased from 11.8×10-2 to 0.95×10-2 h %-1 and 2.46×10-2 to 2.06×10-2 %, respectively, with increasing temperature. The effective diffusivity was evaluated by fitting experimental absorption data to Fick's second law of diffusion. Effective diffusivity of water varied from 8.376×10-12 to 2.22×10-12 m2.s-1 over the temperature range studied, with an energy activation of 24.21 kJ.mol-1. The temperature dependence of the diffusivity coefficient was described satisfactorily by Arrhenius-type relationship.
Keywords — Peleg's Model. Soaking. Sorghum. Water Absorption.
I. INTRODUCTION
Sorghum (Sorghum bicolor L. Monench) is an important crop in semiarid tropics of Africa and Asia, and constitutes a major source of carbohydrates and proteins for people living in these regions. In developing countries the commercial processing of this locally grown grain into value-added food and beverage products is an important driver for economic development (Good et al., 2002). Lately there has been a growing research in sorghum with respect to its potential for starch production (Buffo et al., 1998). Recently, production of malt from wheat, sorghum and other cereal grains rather than barley has begun in the world. In the malting process, carefully selected grains are soaked in water until saturation before germination. In malting process, steeping time and temperature had a highly significant effect on malt quality (Briggs, 1997). Adding water is also a pretreatment for the flour milling process (tempering). The kinetics of water absorption has been extensively studied for traditional food products such as cereal grains and legumes (Abu-Ghannam and McKenna, 1997; Hung et al., 1993; Sopade et al., 1992; Turhan et al., 2002).
Mathematical modeling of hydration process is known to be important for the design and optimization of food process operations. These models are classified to theoretical, empirical and semi-empirical, and despite of the widespread application of computers and their associated softwares, empirical equations are still extensively used in view of their simplicity and ease of computation (Turhan et al., 2002; Sopade et al., 2007). Peleg's equation is popular empirical non-exponential model and some of its parameters are of immense practical significance in hydration kinetics that applied to weight gain during rehydration (Peleg, 1988; Singh and Kulshrestha, 1987; Turhan et al., 2002; Sopade et al., 2007; Cunningham et al., 2007)
Peleg (1988) proposed a two-parameter sorption equation and tested its prediction accuracy during water adsorption of food products. The original form of the Peleg model is as in Eq. (1), which can be rearranged to Eq. (2):
 | (1) |
 | (2) |
It follows that the absorption rate at the beginning of soaking process is expressed subsequently as showing that k1 is linked to water absorption rate, R0 (Peleg 1988).
 | (3) |
The Peleg capacity constant, K2, relates to maximum attainable moisture content. As t → ∞, Eq. (4) gives the relation between equilibrium moisture content (Me) and K2:
 | (4) |
To authors' knowledge there is no information about soaking of sorghum. Therefore, this study was carried out to evaluate the physical properties of sorghum kernel and determine the applicability of Peleg's equation in modeling of water absorption and also to find out the diffusivity and activation energy of sorghum kernel during soaking at different temperatures.
II. MATERIALS AND METHODS
A. Sample preparation
Sorghum (Sorghum bicolor L. Monench) samples harvested in 2007 were obtained from the Karaj field crops Research Institute, Tehran, Iran. Samples were cleaned manually to remove foreign materials and broken, cracked and damaged grains, then sealed in polyethylene bags and stored at 4°C until experiments. Official AOAC (2006) methods were used to determine moisture, fat, ash and protein contents of samples. All experiments were conducted in triplicate and reagents were analytical grades.
B. Determination of Physical properties
In order to determine dimensions, one hundred kernels were randomly selected. For each Sorghum kernel, the three principal dimensions, namely length, width and height were measured using an electronic digital caliper (GUANGLU, China) having a resolution of 0.01 mm. The geometric mean diameter (Gmd) and degree of sphericity ( ) of Sorghum kernels were calculated using the following relationships (Kashaninejad et al., 2006):
) of Sorghum kernels were calculated using the following relationships (Kashaninejad et al., 2006):
 | (5) |
 | (6) |
C. Determination of water absorption kinetics
To determine the kinetics of water absorption, five gram of sample was weighted and soaked in 5 times weigh of distilled water at five temperatures 10, 20, 30, 40 and 50°C for 600 min. During soaking, grains were periodically removed from incubator, superficially dried with paper towels and weighted using an electronic balance (END, 0.0001 gr, Japan). At each interval, the water content of the kernels was calculated as the difference between the weight of the dry solid and soaked kernels. The variation of the moisture content of the grains with time was used to plot the kinetic curve of samples moisture.
D. Determination of the effective diffusivity and activation energy
In order to eliminate the effect of the seed radius on the constant rate of diffusion, the effective diffusivity was calculated in analogy with the analytical solution of one dimensional Fick's law of diffusion with constant moisture diffusivity for sphere given by Kaptso et al. (2008). In this respect, the following equation was used:
 | (7) |
The obtained diffusivity coefficients were correlated with the reciprocal of the absolute temperature, according to the Arrhenius type Eq. (8) and activation energy was calculated by linear regression of Ln(Deff) versus 1/T:
 | (8) |
III. RESULTS AND DISCUSSION
A. Physico-chemical properties of sorghum
Some physico-chemical properties of sorghum kernels are given in Table 1. The length, width, height and geometric mean diameter of the kernels were determined to be 4.77± 0.33, 3.85± 0.43, 2.74± 0.19 and 3.63±0.22 mm, respectively. The results are comparable with previous study by Mwithiga and Sifuna (2006) that reported the average length, width and height of sorghum kernels were 4.04± 0.04, 3.50± 0.03 and 3.61± 0.05 mm, respectively, at a moisture content of 12.33% (d.b.). The sphericity of the kernels at the moisture content of 11.96 (% db) determined using Eq. 7 was 0.764±0.05. The 1000 grain weight of sorghum kernels was 28.37±0.52 g..
Table 1. Average physio-chemical analysis of sorghum (g/100 g dry weight)
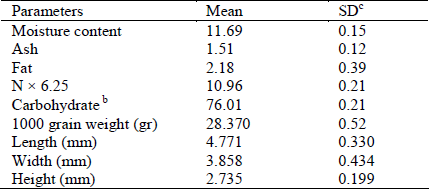
b By difference from 100%.
c Standard deviation.
B. Kinetics of Water absorption
The moisture content (on a dry weight basis) of sorghum kernels calculated at five soaking temperatures during hydration process is shown in Fig. 1. A regular increase in water absorption was observed as temperature increased from 10 to 50°C. This phenomenon can be linked to high rate of water diffusion at higher temperature. These observations are in agreement with other studies (Sopade and Obekpa, 1990; Pan and Tangratanavalee, 2002; Chiang and Yeh, 2002; Moreira et al., 2008; Kaptso et al., 2008).

Figure 1. Comparison of predicted and experimental moisture content of sorghum at different soaking temperatures, solid lines represent predicted values.
Figure 1 indicates that the rate of water absorption is initially rapid and then slows down as equilibrium approaches. This asymptotic behavior is related to the decrease of driving force for water transfer as hydration progresses and the system is close to equilibrium. This effect was also observed during water soaking of rice and Lupin (Bello et al., 2004; Solomon, 2007). The water absorption data of the samples in terms of moisture content under the experimental conditions was fitted to Peleg's equation (Eq. 1), the predicted values were close to the experimental moisture content.
C. The constant rate of water absorption
Plot of t/(Mt -Mo) versus soaking time (t) allows to study the characteristics of Peleg's constants (Fig. 2). The Peleg's rate constant (k1) and capacity constant (k2) determined at different temperatures are presented in Table 2. The R2 values greater than 0.99 confirms the adequacy of the equation for describing the water absorption kinetics of sorghum within the studied temperature range. In this study, K1 values were inversely related to temperature that indicates the increasing of water absorption rate at higher temperatures. This result is in agreement with previous studies for different beans, peas and cereal grains (Sopade and Obekpa, 1990; Sopade et al., 1992; Hung et al., 1993; Abu-Ghannam and McKenna 1997; Turhan et al., 2002; Resio et al., 2006).

Figure 2. Fitting of water absorption data during soaking of sorghum to the Peleg's model.
Table 2. Average Peleg's constants and equilibrium moisture content of sorghum kernels

It is observed that the Peleg's constant K2 for sorghum kernels can be a function of temperature (Fig. 3). Similar trends have been observed for chickpea (Turhan et al., 2002), pigeon pea (Sing and Kulshrestha, 1987) and unblanched red kidney beans (Abu-Ghannam and McKenna, 1997) while other workers (Sopade and Obekpa, 1990; Hung et al., 1993) have reported that K2 can be independent of temperature.

Figure 3. Effect of temperature on the Peleg's capacity constant (K2) during soaking of sorghum kernels.
Table 2 shows the constant K2 decreased from 0.0246 to 0.0206 while the soaking temperature increased from 10 to 50°C. This is due to increasing of water absorption capacity of sorghum with increasing of temperature. This statement clearly confirms that as soaking temperature increases the equilibrium moisture content of sorghum kernel increases too (Table 2).
D. Effective diffusivity and activation energy
The effective diffusivity of kernels calculated by Eq. (7) is shown in Table 3. The effective diffusivity of the kernels increased from 2.22×10-12 to 8.376×10-12 m2s-1 as the soaking temperature increased from 10 to 50ºC. The comparison of the diffusion coefficients for water soaking obtained in this study for sorghum kernels with those reported in the literature for other grains indicates that the effective diffusivity of sorghum kernels is very similar to other agricultural materials (Resio et al., 2006; Bello et al., 2004).
Table 3. Arrhenius parameters for water absorption of sorghum

The logarithm of Deff as a function of reciprocal of absolute temperature (T) is plotted in Fig. 4. The results show a linear relationship between (log Deff) and (1/T) or an Arrhenius-type relationship (Eq. 8). The diffusivity constant (D0) and activation energy (Ea) calculated from the linear regression were 6.39×10-4 (m2 s-1) and 24.21 (kJ mol-1), respectively. The obtained activation energy is in reasonable agreement with the data presented by several authors for other grains. For example Kaptso et al. (2008) found Ea values for cowpea and bambara groundnuta 37.62 and 35.69 kJ mol-1 respectively. Resio et al. (2006) found out the activation energy of 32.1 kJ mol-1 for amaranth grain. Solomon (2007) reported the activation energy of 60.44 kJ mol-1 for lupin seeds and Maskan (2002) reported 11.979 kJ mol-1 as activation energy for wheat.

Figure 4. Effect of soaking temperature on the effective diffusivity of sorghum kernels.
IV. CONCLUSIONS
Peleg's equation successfully represented the water absorption behavior of sorghum kernels during the soaking process at different temperatures and could be used to estimate the moisture content at given soaking time and temperature within the experimental condition considered. The Peleg's constants K1 and K2 were a function of temperature for sorghum and decreased with increase in soaking temperature. The effective diffusivity of sorghum increased with increase in temperature according to the Arrhenius type relationship which the activation energy can be calculated. This study revealed that it is possible to predict the water absorption characteristics of sorghum kernels which can help optimize soaking conditions.
NOMENCLATURE
| D0 | Diffusion constant,(m2 s-1) |
| Deff | Effective diffusivity,(m2 s-1 ) |
| Ea | Activation energy,(kJ mol-1 ) |
| Gmd | Geometric mean diameter, r (mm) |
| H | Height of kernel, (mm) |
| L | Length of kernel, (mm) |
| K | Soaking constant, ( s -1) |
| K1 | Peleg rate constant, (h %-1) % MC db) |
| K2 | Peleg capacity constant, (%-1) % MC db) |
| Mo | Initial moisture content, (% db) |
| Me | Equilibrium moisture content, (% db) |
| Mt | Moisture content at a known time, (% db) |
| r | Sample radius, (m) |
| R | Universal gas constant,( 8.314 kJ mol-1 K-1) |
| R2 | Coefficient of determination |
| t | Soaking time, (min) |
| T | Absolute temperature, (K) |
| W | Width of kernel, (mm) |
 | Sphericity, (%) |
REFERENCES
1. Abu-Ghannam, N. and B. McKenna, "The application of Peleg's equation to model water absorption during the soaking of red kidney beans (Phaseolus vulgaris L.)," Journal of Food Engineering, 32, 391-401 (1997). [ Links ]
2. AOAC, Official methods of analysis,Association of Official Analytical Chemists (18th ed), Washington DC. (2006). [ Links ]
3. Bello, M., M.P. Tolaba and C. Suarez, "Factors affecting water uptake of rice grain during soaking," Lebensmittel-Wissenschaft und-Technologie, 37, 811-816 (2004). [ Links ]
4. Briggs, D.E., Malts and Malting, Chapman & Hall, London (1997). [ Links ]
5. Buffo, R.A., C.L. Waller and A.N. Parkhurst, "Relationship among grain sorhum quality factors," Cereal Chemistry, 75, 100-104 (1998). [ Links ]
6. Chiang, P.Y. and A.I. Yeh, "Effect of soaking on wet milling of rice," Journal of Cereal Science, 35, 85-94 (2002). [ Links ]
7. Cunningham, S.E., W.A.M. McMinn, T.R.A. Magee and P.S. Richardson, "Modelling water absorption of pasta during soaking," Journal of Food Engineering, 82, 600-607 (2007). [ Links ]
8. Good, D.L., C. Halbert and E.K. Arendt, "Mashing studies with unmalted sorghum and malted barley," Journal of Institute of Brewing, 108, 465-473 (2002). [ Links ]
9. Hung, T.V., L.H. Liu, R.G. Black and M.A. Trewhella, "Water absorption in chickpea (C. arietinum) and eld pea (P. sativum) cultivars using the Peleg model," Journal of Food Science, 58, 848-852 (1993). [ Links ]
10. Kaptso, K.G., Y.N. Njintang, A.E. Komnek, J. Hounhouigan, J. Scher and C.M.F. Mbofung, "Physical properties and rehydration kinetics of two varieties of cowpea (Vigna unguiculata) and bambara groundnuts (Voandzeia subterranea) seeds," Journal of Food Engineering, 86, 91-99 (2008). [ Links ]
11. Kashaninejad, M., A. Mortazavi, A. Safekordi and L.G. Tabil, "Some physical properties of pistachio (Pistacia vera L.) nut and its kernel," Journal of Food Engineering, 72, 30-38 (2006). [ Links ]
12. Maskan, M., "Effect of processing on hydration kinetics of three wheat products of the same variety," Journal of Food Engineering, 52, 337-341 (2002). [ Links ]
13. Moreira, R., F. Chenlo, L. Chaguri and C. Fernandes, "Water absorption, texture, and color kinetics of air-dried chestnuts during rehydration," Journal of Food Engineering, 86, 584-594 (2008). [ Links ]
14. Mwithiga, G. and M.M. Sifuna, "Effect of moisture content on the physical properties of three varieties of sorghum seeds," Journal of Food Engineering, 75, 480-486 (2006). [ Links ]
15. Pan, Z. and W. Tangratanavalee, "Characteristics of soybeans as affected by soaking conditions," Lebensmittel-Wissenschaft und-Technologie, 36, 143-151 (2003). [ Links ]
16. Peleg, M. "An empirical model for the description of moisture sorption curves," Journal of Food Science, 53, 1216-1219 (1988). [ Links ]
17. Resio, C.A., R.J. Aguerre and C. Suarez, "Hydration kinetics of amaranth grain," Journal of Food Engineering, 72, 247-253 (2006). [ Links ]
18. Singh, B.P.N. and S.P. Kulshrestha, "Kinetics of water sorption by soybean and pigeonpea grains," Journal of Food Science, 52, 1538-1544 (1987). [ Links ]
19. Solomon, W.K., "Hydration kinetics of lupin seeds," Journal of Food Processing and Engineering, 30, 119-130 (2007). [ Links ]
20. Sopade, P.A. and J.A. Obekpa, "Modelling water-absorption in soybean, cowpea and peanuts at three temperatures using Peleg equation," Journal of Food Science, 55, 1084-1087 (1990). [ Links ]
21. Sopade, P.A., E.S. Ajisegiri and M.H. Badau, "The use of Peleg's equation to model water absorption in some cereal grains during soaking," Journal of Food Engineering, 15, 269-283 (1992). [ Links ]
22. Sopade, P.A., P. Yu Xun, P.J. Halley and M. Hardin, "Equivalence of the Peleg, Pilosof and Singh-Kulshrestha models for water absorption in food," Journal of Food Engineering, 78, 730-734 (2007). [ Links ]
23. Turhan, M., S. Sayar and S. Gunasekaran, "Application of Peleg model to study water absorption in chickpea during soaking," Journal of Food Engineering, 53, 153-159 (2002). [ Links ]
Received: July 18, 2009.
Accepted: November 18, 2009.
Recommended by Subject Editor: Ricardo Gómez.














