Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. vol.41 no.1 Bahía Blanca ene. 2011
ARTICLES
Simulation of wood drying stresses using CVFEM
C. H. Salinas, C. A. Chavez, Y. Gatica♠ and R.A. Ananias♣
Departamento de Ingeniería Mecánica, Universidad del Bío-Bío, Av. Collao 1202, Concepción, CHILE.
casali@ubiobio.cl
Master's Program (c), Ciencias y Tecnología de la Madera, Universidad del Bío-Bío, Av. Collao 1202, Concepción, CHILE. crchavez@alumnos.ubiobio.cl
♠ Doctoral Program (c), Ciencias e Industrias de la Madera, Universidad del Bío-Bío, Av. Collao 1202, Concepción, CHILE. ygatica@ubiobio.cl
♣ Departamento de Ingeniería en Maderas, Universidad del Bío-Bío, Av. Collao 1202, Concepción, CHILE.
ananias@ubiobio.cl
Abstract - The drying of solid wood and associated stresses were simulated by applying the Control Volume Finite Element Method (CVFEM) to a transversal section of solid wood on the radial/tangential plane. The transport of moisture content and stresses produced by its gradients associated with the phenomena of shrinkage and mechanical sorption were modeled simultaneously. In particular, we used a CVFEM program (Fortran 90) that allows integrating a differential equation of non-linear transient diffusion, defining triangular finite elements with linear interpolation of the independent variable within itself. The model was validated by comparing the experimental and analytical results available in the specialized literature. Finally, we showed the original results of the simulation applied to the drying of aspen wood(Populus tremuloides) at three drying temperatures.
Keywords - Simulation; Drying; Wood; Stress; CVFEM.
I. INTRODUCTION
The present study focuses on heat and mass transfer coupled with strain/stress problem during drying process in terms of modeling and simulating the drying of solid wood. A collection of related works can be found in Turner and Mujumdar (1997) and an updated review of these methods is given in Hernandez and Quinto (2005).
In particular, Cloutier and Fortin (1994) develops a numerical model that predicts the drying curve using the water potential model. In the present works, this model is adopted to simulate the transport of moisture content within the wood as described in Salinas et al. (2004).
The effects of heat and mass transport cause strain/ stress within the wood. Modeling this phenomenon is a complex process due to the effects that the drying process produces on the wood. These lead to stresses that cause permanent and transitory deformations due to variations of moisture contents.
The models proposed for wood focus mainly on deformations caused by the transport of energy (temperature) and mass (moisture content). Some works (Perre et al., 1993; Chen et al., 1997; Pang, 2000; Pang, 2007) propose one-dimensional models for determining the deformations resulting from heat and mass transport; notably, deformation by shrinkage and mechanical sorption. Likewise, in two-dimensional (Turner and Ferguson, 1995; Lin and Cloutier, 1996; Ferguson, 1998; Kang and Lee, 2004) and three-dimensional (Ormarsson et al., 2003) models have been proposed for deformation.
Numerically, we use the Control Volume Finite Element Method (CVFEM) to solve the transport and deformation equations induced during the drying process. In general terms, the method CVFEM consists of a Finite Volume that is made up with Finite Elements. This model offers advantages related mainly to its intrinsic quality of conservatively given by Finite Volume Method and the topological versatility bestowed by Finite Elements Method (Baliga and Patankar, 1983).
Thus, we consider linear orthotropic variations of the properties and independent variables within the Finite Element, considering the discrete variable centered on the Control Volume. The numerical approach leads to the formulation of linear algebraic equations systems that are solved through iterative and direct methods (Gauss Saidel with SOR and Gauss Elimination, Lapidus and Pinder, 1982).
The aim of the present work is concerning with simulation of the drying/stress problem, following systematic variations of geometric and physical parameters for the analysis of stability and consistency of the algorithms developed. Moreover, we validate the results obtained by comparing them with the experimental, numerical and analytical data available in the literature.
II PHYSICAL MODEL
We study a physical model of the wood strain/stress problem during drying process. We consider the non-uniform transitory effects induced by the variation in the moisture content (M); that is: stress (sij), strain (eij), and displacements (ui = (u,v)).
As shown in Fig. 1, we consider a transversal two-dimensional section of wood on the radial-tangential plane. The properties are given in Table 1 (Cloutier et al., 1992). The dimensions of this piece of wood are: wide L=0.045 (m) and thickness H=0.045 (m).

Figure 1. Diagram of the physical problem: Transversal section of wood on the radial-tangential plane with non-uniform transient variations in moisture content.
Table 1: Wood properties

The initial and contour conditions are: a) for the problem of moisture content transport, initial moisture content of M=Mini, Neumann-type contour conditions of no-flow on the symmetry axes (x=L/2 and y=0), and surface convection of x=0 and y=H/2; and b) for the strain/stress problem, a non-deformed initial state (sij=eij=ui=0), Dirichlet-type contour conditions on the symmetry axes (u=0 on x=L/2 and v=0 on y=0), and free contour conditions on the surfaces x=0 and y=H/2.
III MATHEMATICAL MODEL
The mathematical model considers that the local variation in the concentration of moisture content, equivalent to the flow divergence, can be written according to the model proposed in (Cloutier and Fortin, 1994). That is:
 | (1) |
where C is the concentration of moisture content (kgwater/kgwood-moist) and qm is the flow of moisture content (kgwater/m2wood-moists).
Assuming small variations in temperature and wood water in equilibrium, the flow can be described in function of conductivity and water potential as 1:
 | (2) |
In particular, as implemented in Salinas et al. (2004), the transport is described indirectly through the water potential ψ (J/kg), considering wood to be a two-dimensional orthotropic medium on the plane x, y. This can be expressed as1:
 | (3) |
where kxx, kyy conductivity (kg2water/mwood-moistsJ) and  capacity (kg2water/Jm3wood-moist).
capacity (kg2water/Jm3wood-moist).
The physical transport parameters to be determined experimentally are conductivity kxx and kyy in the main directions X and Y, respectively, and the variation of moisture content in relation to the potential (∂ M / ∂ ψ).
Alternatively, Eq. 3 can be expressed based on the moisture content (M).
 | (4) |
| where |  |
The mathematical model for two-dimensional deformation resulting from the mechanical equilibrium applied to each point in the absence of a body force can be written as Zienkiewicz and Taylor (2000).
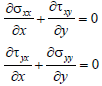 | (5) |
In terms of the gradient, this results in:
∇σi = 0 to i = 1,2 (6)
| where |  | two-dimensional gradient |
σ1 = (σxx, τxy) stress in x
σ2 = (τyx, σyy) stress in y.
The non-uniform distribution of moisture content produces stress induced by free deformation and stress sustained over time. The modeling of these stresses can be done through an implicit function of five parameters that define an initial deformation ε0: shrinkage α, mechano sorptive creep coefficient m, stress σ, variation of concentration ΔC and, in the case of plane deformation, the Poisson ratio v. That is:
 | (7) |
Thus, the stresses are determined based on the following expression:
σ = D(ε - ε0) + σ0 (8)
where σ0 represents the values of the initial stresses and D is the elasticity matrix of material.
In order to implement the Initial Deformation Method, the aforementioned problem is integrated over time in discreet terms (Turner, 1996). For this, ΔC is considered to be the variation in moisture content between time tn = ndt and time tn + 1 = (n + 1)dt where dt is the interval of time considered; that is: ΔC = Cn+1 - Cn and, likewise, Δσ = σn + 1 - σn and Δε0 = εn + 1 - ε0n. Thus, we can pose the following expression that describes the stress mentioned in time tn+1 as a totally explicit function of the variables and/or parameters in time tn. That is:
 | (9) |
The mathematical model for the case of moisture content transport and stress (Eqs. 3, 4, 6) can be presented in the generic form by a non-linear, second-order equation of transient diffusion in which the independent variable is denominated as  (see specific variables and properties in Table 2). That is:
(see specific variables and properties in Table 2). That is:
 | (10) |
Table 2: Variables and properties.

where  is the transported variable, t is time (s),
is the transported variable, t is time (s),  is capacity, Γ is the diffusion coefficient and S = So -
is capacity, Γ is the diffusion coefficient and S = So -  is the source.
is the source.
Considering a volume (domain) ∀; with contour  , we have the following initial and contour conditions:
, we have the following initial and contour conditions:

IV NUMERICAL MODEL
Upon integrating Eq. 10, in domain ∀, according to Green's Theorem, the divergence integral in domain ∀ becomes an integral in the contour Ω. That is:
 | (11) |
where  is the normal external unitary vector to Ω.
is the normal external unitary vector to Ω.
 | is the gradient equal to |  |
Now, considering that domain ∀ made up of by nl Finite Volumes (FV) (∀l with (l = 1, nl)) of contour Ω1 and that, similarly, each FV consists of nk partial contributions of Finite Elements (FE) of contour  with (k = 1, nk) (see Fig. 2), we can write:
with (k = 1, nk) (see Fig. 2), we can write:

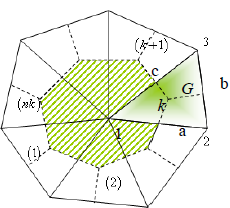
Figure 2. Finite Volume l made up of nk FE.
When considering the term of local variation  and the source term S in the centroid of the FV as predominant and evaluating the temporal term through finite difference at (t=m Δt) with (t=(m-1) Δt) we get:
and the source term S in the centroid of the FV as predominant and evaluating the temporal term through finite difference at (t=m Δt) with (t=(m-1) Δt) we get:
 | (12) |
 | (13) |
The diffusion term  is integrated on the contour of the FE k equal to
is integrated on the contour of the FE k equal to  for time t=m Δt (omitted for simplicity). Thus, and considering that each FV is made up of partial contributions of nk FE, as shown in Fig. 1, the partial diffusive contributions of the FE k to the FV centered on the local nodes li (i=1, 2, and 3) can be written as:
for time t=m Δt (omitted for simplicity). Thus, and considering that each FV is made up of partial contributions of nk FE, as shown in Fig. 1, the partial diffusive contributions of the FE k to the FV centered on the local nodes li (i=1, 2, and 3) can be written as:
 | (14) |
Similar expressions can be written for the contributions centered on l2 and l3. The subscripts a, b and c represent the contour segments  ,
,  and
and  , respectively (see Fig. 2).
, respectively (see Fig. 2).
For the above integration, we define a linear variation  within the FE, that is:
within the FE, that is:
 | (15) |
where A, B and C are constants defined based on the nodal values  ,
,  and
and  , equal to:
, equal to:

According to Eq. 14, the diffusive contribution of the contour defined by the segment  is given by:
is given by:
 | (16) |
and, in consideration of Eq. 15, the gradient of  is equal to:
is equal to:
 | (17) |
The diffusive flows Jx and Jy in the orthotropic directions x and y, when considering diffusion Γ;x and Γy, respectively, are given by:
 | (18) |
With the gradient and normal constant in the contour  , the resulting integral is equal to:
, the resulting integral is equal to:
 | (19) |
where da is segment length  .
.
The normal unitary vectors na is defined as:
 | (20) |
According to these last definitions, we get:
 | (21) |
where

Likewise, we obtain expressions for the contributions of the contour segments  .
.
Thus, the contribution of the element k to the FV l centered on node l1:
 | (22) |
Finally, when considering the transient contributions and those of the source term given by (12) and (13), in addition to the diffusive terms given by (22), the discreet two-dimensional transient diffusion equation posed implicitly for  at t = mΔt in a generic volume l, is given by:
at t = mΔt in a generic volume l, is given by:
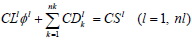 | (23) |
With  and
and  .
.
Thus, for each value l, we obtain an algebraic equation formulated for the average value of  in each subdomain
in each subdomain  , configuring a system of nl x nl equations of the form [A]
, configuring a system of nl x nl equations of the form [A]  ={B}.
={B}.
V RESULTS
The results from the three simulations (moisture content transport in aspen wood, heat diffusion and thermal stresses in a steel plate, and moisture content transport and drying stress in aspen wood) are presented herein. The first two simulations are done in order to validate the computer codes for modeling, respectively, the transport of moisture content and stresses. The third simulation shows an application of this in the context of the wood drying process, which motivated this study.
A. Transport of moisture content in wood
Below are shown results of transient moisture content transport on a two-dimensional section of the aspen wood on the radial-tangential plane. The drying problem is modeling as discussed in the item III, it is illustrated in Fig. 1 and its properties are given in Table 1.
Figure 3 shows a characteristic mesh used in modeling that presents exponential-type refinement towards the surfaces with convection. This type of mesh is optimal for capturing the large moisture content gradients in these regions.

Figure 3. Mesh with 30x30 logarithmic refinement.
In Fig. 4, the consistency and convergence are analyzed in relation to the mesh type (uniform, cosine, and logarithmic element distribution) for moisture content values in the CD layer. We note that the distributions that concentrate the element towards the convection regions best approach the convergent solution.

Figure 4. Moisture Content v/s Mesh analysis.
Figure 5 shows details of the moisture content distribution simulated for T equal to 20, 35 and 50 (ºC). We can see the advance of the drying front: greater concentration of moisture content isolines reflect greater gradients. The orthotropic behavior can be observed in the lack of polar symmetry of the moisture content.

a) 20 ºC.

b) 35 ºC.

c) 50 ºC.
Figure 5. Drying fronts v/s time.
Finally, Fig. 6 shows the results of drying curves obtained by the present model with those experimental results obtained by Cloutier et al. (1992). The good agreement observed shows that this captures the essence of the physical phenomenon under study.

Figure 6. Drying curves with dt=0.1 (h).
B. Heat diffusion and thermal stresses.
The transient two-dimensional simulation of heat transport and the associated stresses was done for a steel plate. The problem is shown in Fig. 7 and the properties are given in Table 3. The plate dimensions are: length L=0.6 (m) and height H=0.2 (m). The contour condition effects considered are: restricted displacement in the Y direction of layer AD (v=0 in y=0), restricting in the X direction in the layer BC (u=0 in x=L), and freedom in the layers CD and DA. Naturally, point B is restricted in X and Y ((u,v)=(0,0) in B). This problem has an analytical solution (Boley and Weiner, 1960).

Figure 7. Two-dimensional steel plate problem
Table 3: Properties of the thermal plate.

The non-uniform distribution of temperatures produces stresses induced by dilatation, as it does when sustained over time (creep). The modeling of these stresses can be done in a manner equivalent to that of stresses presented for the variation of moisture content in wood. In particular, for an initial deformation ε0 in function of: thermal dilatation α, creep coefficient m, stress σ, temperature variation ΔT, and for plane strain, the Poisson ratio ν. The problem was solved with the present algorithm and some results are presented in Fig. 9-11.
Figure 8 shows mappings of the state of strain and stress for t=1 (h). These maps reveal the consistency in terms of the imposition of contour conditions (Fig. 8a). The effects of the restrictions to the free deformation added to the creep phenomenon in terms of its qualitative consistency can be appreciated in Fig. 8b. The analysis of convergence and consistency related to the size contrasted with the analytical solution, as shown in Fig. 9. As can be seen, transitory convergent results can be obtained with uniform meshes of 50x20.

a) Displacement u.

b) Normal stress
Figure 8. Stress and displacement: t= 1, dt=0.01 (h).

Figure 9. Normal stress σxx: Point B, dt=0.01 (h).
Finally, Fig. 10 shows the results of the distribution of normal stresses in the direction x (σxx) of the BC layer, contrasting with the analytical results. This agreement reflects appropriate modeling of the stress/strain problem under study.

Figure 10. Normal stress σxx: BC layer, dt=0.01(h).
C. Moisture content and drying stresses.
Below are shown results of computer code for moisture content coupled with strain/stresses problem in a piece of aspen wood during the drying process. For this, we determine, in each time of integration, the distribution of moisture content that allows a later calculation of the free deformations ε0 that motivate drying stresses.
Figure 11 shows spatial distributions of the calculation parameters for the strain/stress problem for the permanent state (400 h) and drying temperature equal to 50ºC. In Fig. 11a and 11b, are we can appreciate the implementation of the contour conditions and as the greatest displacements concentrate on the restriction of a degree of freedom. Figure 11c and 11d show in detail how the normal stresses concentrated in A, B, and C (see Fig. 1), focusing on tension in A and C (surface) and compression in B (center). On the other hand, the shear stresses are shown in Fig. 11e concentrate on the diagonal slightly displaced towards point D (surface).
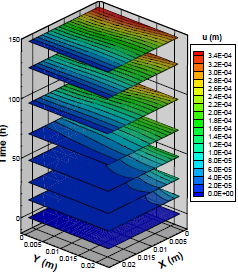
a) Displacement u (Radial).

b) Displacement v (Tangential).

c) Stress σxx
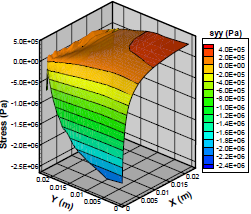
d) Stress σxx

e) Stress Γxy
Figure 11. Strain and displacement: T=50ºC, t=400 (h).
Figure 12 show the transitory normal stress σxx at centerline X=L/4, split in two drying stage according to fiber saturation point (FSP): Figure 12a, show 1º Stage, upper FSP, where the center have compressive stresses, induced by tensile effort in the surface. And Fig. 12a, show 2º Stage, under FSP, where the center became a developed tensile stresses, as a reaction to contraction. In these pictures we can see how the cross section of timber is subjected to tensile and compressive during drying process, which are highly variables.

a) 1º Stage.

b) 2º Stage.
Figure 12. Normal stress σxx at centerline.
Figure 13 shows the transitory evolutions of the stresses in the center and the surface of the domain of calculation, points B and C of Fig. 1 for three drying temperature (20, 35 y 50 ºC). There, the dynamic of the variation of the intensities of the normal stresses can be appreciated. Basically, at the onset of drying on the surface and in the center, we observe a marked tension and slight compression, respectively. This contrasts with the final state of stresses at the end of the drying, in which the normal stresses are inverted. The latter is one of the relevant characteristics of the simulated physical problem. Furthermore, we can see that the residual stress are very similar for three cases studied, but there are strong differences in the stress transitory evolution, specially, how the stresses are inverted. Of course, at initial drying the surface stress have one oscillatory performance because the critical drying condition.

a) 20 ºC.

b) 35 ºC.

c)50 ºC.
Figure 13. Transitory stress σxx Mesh Log 30x30.
VI CONCLUSIONS
The results presented in Fig. 3-6 lead us to conclude that the two-dimensional simulation of moisture content transport modeled according to water potential was effective.
The results given in Fig. 7-10 show that an effective simulation was also done for the stress/strain phenomenon caused by free deformations and the associated creep phenomenon.
The results of the application shown in Fig. 11-13 indicate consistent qualitative results, in terms of the simulation of the phenomenon of moisture content transport correlated with the stresses associated with the moisture content gradients during the transient process of wood drying.
Furthermore, are not high differences in residual stresses for drying temperature studied. Nevertheless there are hard differences in how the transitory stress are performed, specially when are compared stresses in the center versus surface.
1 Because the coefficients cψ, kxx and kyy are now dependent on the variable transported and, in the case of conductivity, also on direction, these configure non-linear, orthotropic mass transport.
REFERENCES
1. Baliga, B.R. and S.V. Patankar, "A control volumen finito element method for two dimensional incompressible Fluid flow and heat transfer," Num. Heat Transfer, 6, 245-261 (1983). [ Links ]
2. Boley, B.A. and J.H. Weiner, Theory of Thermal Stresses, John Wiley and Sons, Inc., New York (1960). [ Links ]
3. Chen, G., R.B. Keey and J.f.C. Walker, "The drying stress and check development on high-temperature kiln seasoning of sapwood," Pinus radiate boards. Holz als Roh-und Werkstoff, 55, 59-64 (1997). [ Links ]
4. Cloutier, A. and Y. Fortin. "Wood drying modelling based on the water potential concept: Effect of the hysteresis in the M-ψ relationship," Drying Tech., 12, 1793-1814 (1994). [ Links ]
5. Cloutier, A., Y. Fortin and G. Dhatt, "A wood drying finite element model based on the water potential concept," Drying Technology, 10, 1151-1181 (1992). [ Links ]
6. Ferguson, W.J., "The control volume finite element numerical solution technique applied to creep in softwoods," Int. J. Solid Structures, 35, 1325-1338 (1998). [ Links ]
7. Hernandez, R. and P. Quinto, "Secado en Medios Porosos: Una Revisión a las Teorías Actualmente en Uso," Cinética, 9, 63-71 (2005). [ Links ]
8. Kang, W. and J.H. Lee, "Simple analytical methods to predict one-an two-dimensional drying stresses and deformations in lumber," Wood Sci. Tech., 38, 417-428 (2004). [ Links ]
9. Lapidus, L. and G.F. Pinder, Numerical solution of partial differential equations in science and engineering, John Wiley & Sons, Inc. (1982). [ Links ]
10. Lin, J. and A. Cloutier, "Finite element modelling of the viscoelastic behaviour of word during drying," 5th IUFRO International wood drying conference, 117-122 (1996). [ Links ]
11. Ormarsson, S., D. Cown and O. Dahlblom, "Finite element simulations de moisture related distortion in laminated timber products of norway spruce and radiata pine," 8th IUFRO International wood drying conference (2003). [ Links ]
12. Pang, S., "Modelling of stress development during drying and relief during steaming in Pinus radiate lumber," Drying Technology,18, 1677-1696 (2000). [ Links ]
13. Pang, S., "Mathematical modeling of kiln drying of softwood timber: Model development, validation and practical application," Drying Technology, 25, 421-431 (2007). [ Links ]
14. Perre, P., M. Moser and M. Martin, "Advances in transport phenomena during convective drying with superheated steam and moist air," Int. Journal of Heat and Mass Transfer, 36, 2725-2746 (1993). [ Links ]
15. Salinas, C., R. Ananias and M. Alvear, "Simulación del secado convencional de la Madera," Maderas Ciencia y Tecnología, 6, 3-18 (2004). [ Links ]
16. Turner, I. and A.S. Mujumdar, Mathematical modeling and numerical techniques in drying technology, Marcel Dekker Inc., New York (1997). [ Links ]
17. Turner, I.W. and W.J. Ferguson, "Unstructured mesh cell-centered control volume method for simulating heat and mass transfer in porous media: Application to softwood drying, part I and II," Appl. Math. Modeling, 19, 654-674 (1995). [ Links ]
18. Turner, I.W., "A two dimensional orthotropic model for simulating wood drying process," Applied Mathematical Modeling, 20, 60-81 (1996). [ Links ]
19. Zienkiewicz, O.C. and R.L. Taylor, The Finite Element Method, Fifth edition, published by Butterworth-Heinemann (2000). [ Links ]
Received: November 2, 2009.
Accepted: January 11, 2010.
Recommended by Subject Editor: Eduardo Dvorkin.














