Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. vol.41 no.2 Bahía Blanca abr. 2011
ARTICLES
Modeling and testing of moving base manipulators with elastic joints
M. H. Korayem and H. R. Heidari
Robotic Research Laboratory, College of Mechanical Engineering,
Iran University of Science and Technology, Tehran, Iran.
hkorayem@iust.ac.ir
Abstract - In this paper, design and manufacturing of a manipulator with joint elasticity is described while different base positions are considered. First, the kinematics and dynamic equations of the mechanism with flexible joints for the three major axis of the mobile robot are derived and simulated. Next, computational technique for obtaining maximum load carrying capacity of robotic manipulators with joint elasticity is described while different base positions are considered. The maximum load carrying capacity that can be achieved by a robotic manipulator during a given trajectory is limited by number of factors. Probably the most important factors are the actuator limitations, joint elasticity (transmissions, reducers and servo drive system) and relative configuration of robot with respect to its base. Finally, the manipulator is tested for a given trajectory in order to find the characteristics of the designed manipulator. While the manipulator is designed to carry the maximum load, end-effector's speed, robot's compatibility with the operator's condition, and accuracy are the most important applicable points of the manipulator. Therefore, the manipulator in different trajectories with various speeds and loads are tested, and then the results are analyzed.
Keywords - Modeling and Simulation; Manipulator; Flexible Joints.
I. INTRODUCTION
Today, one of the most important problems in the modern industrial companies is difficulties in the manufacturing for operators. In addition, in the automation, which needs operator's accuracy and swiftness, manipulating might cause errors in measurement especially in hard working situations. This hard work situation not only might hurt labor but also cause unqualified production. Efficiency is the main purpose in manipulators usage in industries and they are tremendously used in carrying pieces. The use of industrial mechanisms especially robotic manipulators in production industry has been very important worldwide. For many industrial applications, current robotic manipulators with flexible joint are relatively slow even when they are not fully loaded, so it is hard to justify their use economically. Their speed, load-carrying capacity, and hence their productivity, are limited by the deflection of the end-effector and the capability of their actuators. Increasing actuator size and power is largely self-defeating, because of increased cost and power consumption of the larger actuators as well as increased inertia of the actuators themselves. Consequently, a more successful approach should be to maximize the load-carrying capacity of the flexible manipulator, subject to the constraints imposed by actuator capacity and allowable end-effector deflection for a given dynamic trajectory.
Works on load-carrying-capacity problems for manipulators have applications in advanced trajectory planning, design and selection of robot manipulators. For instance, Wang and Ravani (1988) were shown the maximum allowable load of a fixed base manipulator on a given trajectory is primarily constrained by the joint actuator torque and its velocity characteristic. Thomas et al. (1985) used the load capacity as a criterion for sizing the actuator at the design stage of robotic manipulators. In their study, they considered the maximum load in the neighborhood of a robot configuration. A technique was also developed in Wang and Ravani (1988) to maximize the DLCC of an entire trajectory, rather than in the neighborhood of a configuration. In this work, piece-wise rigid links and joints were assumed. Korayem and Basu (1994a,b), by relaxing the rigid body assumption, presented an algorithm for computing the Dynamic Load Carrying Capacity (DLCC) of elastic manipulators. Yue and Tso (2001) used a finite-element method for describing the dynamics of a system and computed the maximum payload of kinematically redundant manipulators. Korayem and Ghariblu (2003) developed an algorithm for finding the DLCC of rigid mobile manipulators.
The main source of vibration in industrial robot manipulators is the presence of joint elasticity between the driving actuators and the drive links. The origin of elasticity is transmission parts, such as harmonic drives, belts, or long shafts, during high-speed motion or hard contact with the environment (Sweet and Good, 1985; Rivin, 1988). Ider and Ozgoren (2000) studied the inverse dynamic control of a manipulator with elastic joints. A computer modeling was applied to show the accuracy of the results based on a manipulator with 3 degrees of freedom with elastic joints. Gamrraado and Yuhara (1999) obtained interesting results by applying Newton-Euler method to computer modeling for an elastic robot with two arms and revolute joint. Usually, in computing the DLCC by assuming rigid joints and links, the actuator torque limits are considered (Wand and Ravani, 1985), but for the flexible robot, the difference between the allowable deflection and the magnitude of the deflection with added end-effector mass can be introduced as a load coefficient for DLCC determination (Korayem and Basu, 1994a). For a flexible joints 6UPS-Stewart platform, joint actuator torque capacity and the motion accuracy were considered to determine the maximum payload capacity (Korayem and Shokri, 2006). In these papers test and flexibility are not taken into account for determination of the dynamic load carrying capacity.
In this paper, first, the Lagrange's method is used for dynamic modeling of the elastic joint manipulator. The results were obtained for different joint stiffness coefficients for a given trajectory. A method to obtain dynamic load capacity subject to the accuracy and actuator constraints is described. Then, several experimental tests are done on the flexible joints manipulator for the given trajectories. The results depicted the importance of the two constraints. According to the accuracy and tracking, they show which one would be the main. Depending on the operation's requirements or robot's model, manufacturers test the path and end-effectors properties. These tests depend on the operation's requirements and the customer favorite. While the manipulator was designed to carry the automobile petrol tank, end-effector's speed, robot's compatibility with the operator's condition, accuracy and the maximum dynamic load carrying capacity were the most important applicable points of the manipulator. Therefore, by experimenting in various trajectories with different speed and load, we have attained manipulator's characteristics as accuracy, repeatability and DLCC. Finally, the paper reports simulation results as well as successful experiments of implementing the algorithm.
II. INTRODUCING THE MANIPULATOR
This manipulator has 3 revolute joints and a mobile base. These joints make a 360° rotation in the z-axis and ±15 vertical motion (Fig. 1). The schematic of the manipulator is shown in Fig. 2. Due to the rail's horizontal motion and negligible flexibility.

Figure 1: The designed manipulator for carrying automobile petrol tank

Figure 2: Schematic of the manipulator
The position of the end effector in all over path should be determined in order to find the accuracy in the final points. By using encoders in each joints and electronic board, finding position of the rotational axis is possible. Regarding the position of axes, can be found speed and acceleration in each point.
We can control the encoder's position by a computer program, on line. In each interval in the experiment, data of encoder's position can be saved.
Applying kinematics equations, the end-effector's position could be calculated. However, to attain desired goal these parts are needed.
- Three encoders to determine the three major joint's position.
- Intermediate circuit; to convert the pulses and orientation.
- Computer programming; in order to convert and save the information and data.
- Computer for receiving the information.
Each part of the manipulator can be introduced as follows:
A. Encoders
Encoders ENB-500-3-1 as sensitive sensors are used in joint rotational angle measurement. There is a code on each encoder to determine the accuracy. Number 500 shows the number of pulses in each revolution. The accuracy of this encoder is 0.72 degree. The encoder's voltage varies from 5V to 24V. According to the intermediate circuit's voltage, 5V is used.
B. Intermediate circuit
Initially raw signals enter into the intermediate circuit and through a FPGA circuit, used as a signal converter, are converted to processor-friendly ones. Computer and the hardware circuit are connected, using a COM1 port and RS232 standard by 2400 bit per second sending rate.
C. Computer programming
Visual Basic program is used to run computer program, which processes the received information from the encoders. In each time, until all three encoder's data are received, the information would be saved in special array. The diagram would change with renewed information.
D. Computer
All the information, through a serial port No.1, would enter into the computer and computer program would draw refreshing data diagram, which was displayed in Fig. 3.

Figure 3: Computer programming
A controlling pneumatic system, including pneumatic cylinder and a relative regulator is used to balance the load in all the time. There are some compacted pneumatic cylinders as brake to lock the mechanism in any position.
III. MANIPULATOR ERGONOMIC ANALYZING
Manipulators are designed to make system semi-automated and reduce operator's tiredness. Therefore, we should consider ergonomic principles such as balancing the work's surface height and anthropometric, enough space for moving, accessibility of the controls and making the environment labour-friendly and adapting the manipulator with the load, anthropometric and the facilities, fitting knobs with human hand; in designing. Operator's training is important too.
In different manipulator's parts, some ergonomic points are considered.
- Rail System: Aluminum structure, hanger system for suspension, trolley system for frictionless movement, and accessories like end stops; allow effortless movements of load in a single line.
- Balancer System: using various control modules, allows zero gravity manipulation of load and the handles grippers or tackles.
- Jib Boom Systems: allow floor or roof mounted single point support for a cantilevered transportation of the load.
- Manipulator arm: these articulated arms allow the load to be manipulated with a rigid mechanical support that allows offset or cantilevered operation to operate in constrained spaces.
- Driver System: it is composed of dry and oil-free compressed, part grippers and vacuum mechanical tools to carry loads.
IV. KINEMATICS MODELING OF MECHANICAL MANIPULATOR
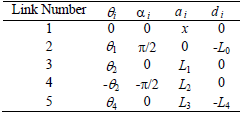
Initially, absolute coordinate and four relative coordinates were selected. Denavit-Hartenberg parameters can be defined for the above mechanism as listed in Table (1).
Table 1: D-H parameters of the given manipulator
A general transformation matrix can be obtained as follows:
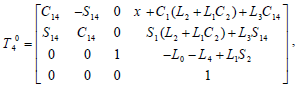 | (1) |
where s12 = sin(θ1 + θ2),c12 = cos (θ1 + θ2) and s14 = sin(θ1 + θ4),c14 = cos (θ1 + θ4). It is obvious that in the above matrix the number of unknowns is greater than the number of equations. As a result, an extra degree of freedom can be seen in the equations. Angular velocity must be calculated using pseudo inverse matrix as below:
 | (2) |
Where J is Jacobian matrix.
V. SIMULATION OF THE MANIPULATOR WITH MATLAB SOFTWARE
In order to initially check the validity of the model, the path traversed by end-effector was determined in 3D space using the following equation (Fig. 4).
X =580+550t Y =250-420t Z =-835+150t -30t2, (3)

Figure 4: 3D diagram of the assumed trajectory
The paths traversed by the end effector attained by experiments and simulation were compared. In simulation, the equations obtained from inverse kinematics modeling were solved for 4 degree of freedom.
VI. DYNAMIC MODELING OF MANIPULATOR WITH ELASTIC JOINTS
For the current modeling of manipulator and load dynamics, it is essential to determine "The maximum load" for a flexible joint robot. The joint deflection or oscillation at higher speed is assumed as much as 25% of the end-effector's deflection. The elasticity at the ithjoint can be modeled as a linear torsion spring having the spring constant ki. Vectors 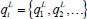 , as the link angles and
, as the link angles and  as the rotor angles defined for the multi-link flexible joint manipulator. A Lagrangian approach was used in order to obtain the dynamic equations of motion for the manipulator with elastic joints, as below:
as the rotor angles defined for the multi-link flexible joint manipulator. A Lagrangian approach was used in order to obtain the dynamic equations of motion for the manipulator with elastic joints, as below:
 | , (4) |
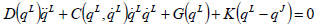 | , (5) |
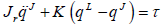 | , (6) |
Where D(qL) is the inertia matrix for the associated rigid system,  is the vector of Coriolis and centripetal forces, G(qL) is the vector of forces due to gravity, K = diag[k1, k2,...,kn] is a diagonal matrix of restoring force constants modeling the joint elasticity, Jr = diag[Jr1,Jr2,...,Jrn] is diagonal matrix representing rotor inertia, and τ and F are the generalized force delivered by the actuator. Each link is moved by an actuator. This motion is transformed to the next link by either gears or belts but in each condition, the elasticity of these joints is reason of elastic coupling between actuator and the link. This elastic coupling behaves like a spring and such modeling is shown in Fig. 5.
is the vector of Coriolis and centripetal forces, G(qL) is the vector of forces due to gravity, K = diag[k1, k2,...,kn] is a diagonal matrix of restoring force constants modeling the joint elasticity, Jr = diag[Jr1,Jr2,...,Jrn] is diagonal matrix representing rotor inertia, and τ and F are the generalized force delivered by the actuator. Each link is moved by an actuator. This motion is transformed to the next link by either gears or belts but in each condition, the elasticity of these joints is reason of elastic coupling between actuator and the link. This elastic coupling behaves like a spring and such modeling is shown in Fig. 5.

Figure 5: Rotational elastic model of joints
In this model, 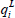 represents the general coordinates of ith link,
represents the general coordinates of ith link,  represents the general coordinates of elastic ith joint, kti represents torsional stiffness coefficient of the ith joint and ui is the applied torque from ith actuator to ith link. According to these, the dynamic equations of the manipulator with an assumed elastic joint were obtained for the trolley and three major joints as shown below:
represents the general coordinates of elastic ith joint, kti represents torsional stiffness coefficient of the ith joint and ui is the applied torque from ith actuator to ith link. According to these, the dynamic equations of the manipulator with an assumed elastic joint were obtained for the trolley and three major joints as shown below:
 | (7) |
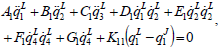 | (8) |
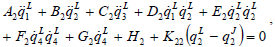 | (9) |
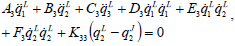 | (10) |
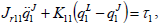 | (11) |
 | (12) |
 | (13) |
Assuming a given trajectory, variation of joints angles are determined from the above differential equations. The graphic representation of the solutions with different torsional stiffness coefficients are depicted in Figs. 6 and 7 for trolley and joints 2, respectively. Joint's torques are shown in Fig. 8.
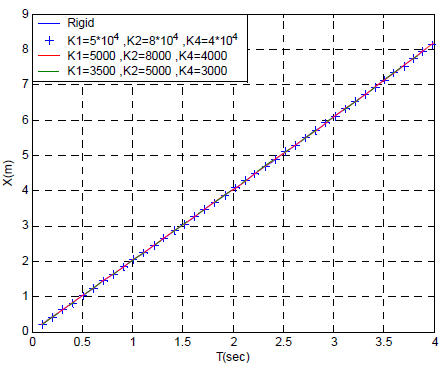
Figure 6: Linear motion of trolley versus time

Figure 7: Angular response of second joint versus time
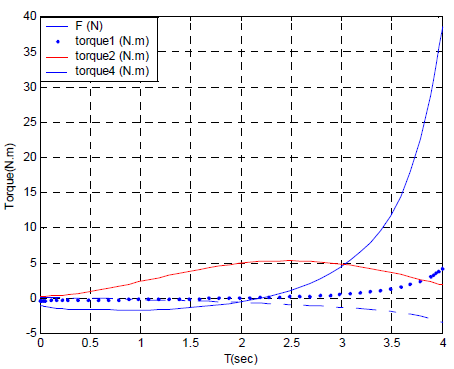
Figure 8: Variation of joint torques with time
As shown in the manipulator angle diagrams (Figs. 6-7), it is seen that increased torsional stiffness coefficient does result in joint stiffness, which in turn reduces vibration in both the joint and the end-effector path. For a very high coefficient, the result shows a solution equivalent to a pure rigid system. Flexibility of joint's drivers and power transport system would include at least 80% of the total flexibility. The main reason of the manipulator deviation is its major joint's flexibility. There is no difference in displacement for different stiffness by neglecting the rail's flexibility, as shown in Fig. 6. However, according to the simulated trajectory and manipulator's structure, the second joint is more sensitive to the stiffness and flexibility.
VII. TESTING THE MANIPULATOR
While the manipulator is designed to carry the automobile petrol tank, end-effector speed, robot's compatibility with the operator's condition, accuracy and the maximum dynamic load carrying capacity are the most important applicable characteristics of the manipulator. Maximum error of a trajectory, accuracy and repeatability are obtained for this manipulator.
Analyzing and modeling this manipulator, it has tested in one, two and three-dimensional various trajectories carrying different loads, in different speeds in the laboratory. Various methods used to control the test and error calculation and surveying different variations, show that flexibility and manipulator's initial condition must be controlled. However, results are acceptable.
VIII. JOINT FLEXIBILITY TESTING IN A CIRCULAR AND OBLIQUE LINE MOTION
Constraining end-effector to move on a purposed trajectory, joint rotation can be measured using the encoders. The results for two-dimensional Circular and three-dimensional Oblique line with in which the end-effector proceed the trajectory in 25 second, are shown in Figs. 9-12. Next, we compared the results with the theoretical equations ones. It shows that the results were acceptable, although, according to the flexibility, human's fluctuation error and the simplicity of the controlling pneumatic circuit, there was 0.08 m error. Figures 9 and 11 show the joint angles in simulation and experiment. Figs. 10 and 12 show the Circular and Oblique line on which the end-effector moves. The pose accuracy and pose repeatability are reported using ISO9283 standard.

Figure 9: The joint angles in simulation and experiment on the Circular path vs. time
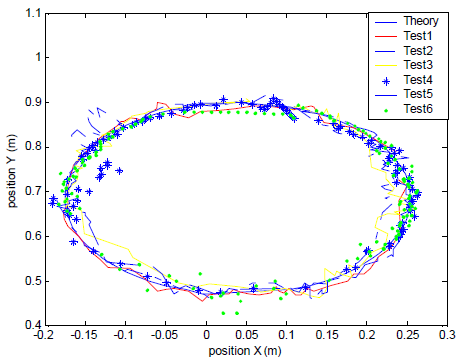
Figure 10: 2D diagram of the Circular trajectory in various tests

Figure 11: The joint angles in simulation and experiment on the Oblique line path

Figure 12: 3D diagram of the Oblique line trajectory in simulation and experiment
A. Pose Accuracy of End-Effector (positioning error)
The manipulator has been guided from a determined point to command pose zc, yc, xc for N times and its actual pose zj, yj, xj is determined. The Eq. 12 calculates the pose accuracy (APp).
 | , (14) |
where:
 | , (15) |
 ,
,  ,
,  is barycentre, has been found in N times repeatability. zj, yj, xj refer to Jth attained pose. The pose accuracy is shown in Fig. 13.
is barycentre, has been found in N times repeatability. zj, yj, xj refer to Jth attained pose. The pose accuracy is shown in Fig. 13.
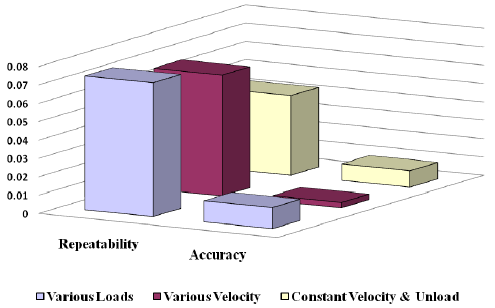
Figure 13: Pose Accuracy and Pose Repeatability of the oblique line trajectory
B. Pose Repeatability
Pose Repeatability refer to the accuracy of attained pose and command pose, which has been found in a determined pose in N times. For a given trajectory, pose repeatability (RPL) refer to the radial of sphere in the center of cluster. As we have shown below:
 |  | , (16) |
where:
 | 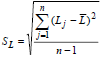 | , (17) |
Pose repeatability for this manipulator is shown in Fig.13.
Flexibility and initial conditions of arm are two important criteria have been controlled in the experiments. The absolute error in each point of the trajectory computed from the difference between the actual quantity and experiments. Maximum absolute errors emax for the Oblique line trajectory are shown in Fig. 14. Variation and Sum square error SSE are two controlling criteria that show the error in each test, as determined in Eqs. 18 and 19.
 | (18) |
 | (19) |
 | (20) |
where nk refer to the number of points, xk to measured quantities and nth to theoretical quantities. Although the experimental results are near to the theoretical, at the end of the trajectory, due to joints flexibility and manufacturing low quality of the manipulator, they diverge. Various controlling is shown in Fig. 20.

Figure 14: Maximum Absolute Error of the Oblique line trajectory
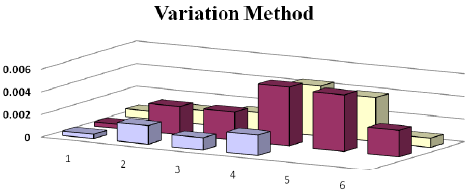
Figure 15: Variation Analyzing of the Oblique line trajectory
IX. END-EFFECTOR'S TRAJECTORY IN VARIOUS SPEEDS TEST
Various speeds and their relation with the error are an important manipulator's characteristics. We tested six different speeds in each trajectory and attained the errors. According to Fig. 14, errors did not change in an Oblique line.
X. END-EFFECTOR'S TRAJECTORY IN VARIOUS LOADS TEST
Maximum load carrying capacity is another important characteristic of a manipulator. Four different loads, 10, 12, 14, 20 Kg have been used in testing and finding the error. Maximum acceptable load depends on the drift from the main trajectory. Increasing load would increase the error and in a trajectory total error calculated in the final point is unacceptable (Fig. 14).
XI. DLCC formulation for a given trajectory
The DLCC of a flexible link manipulator is defined as the dynamic load which the manipulator can carry in performing the trajectory with acceptable precision for a pre-defined trajectory. The dynamic payload-carrying capacity of a robot manipulator is usually defined as the maximum payload that the manipulator can repeatedly lift in its fully extended configuration while the dynamics of both the load and the robot manipulator itself must be taken into account. The maximum DLCC which can be achieved by a manipulator during a given trajectory is limited by a number of factors. The most important ones are; the dynamic specification of the manipulator, the actuator limitations and accuracy. The algorithm illustrates computing procedure for finding DLCC is presented in Korayem et al. (2008).
XII. DISCUSSION
To design a robot, one should consider kinematics and dynamic situations. It needs to solve some complicated long lasting equations. Nevertheless, no experiment could be applied until a prototype has been constructed even the genuine engineers use the simulation software and the prototype. In this study, we have designed a manipulator for automobile petrol tank carrying. Using simulation and coding in commercial software, we have found the manipulator characteristic after kinematics and dynamic studying. Laboratory tests in different trajectories were accomplished and the results were compared with the theory and simulation. As shown in Figs. 6 and 7 joints flexibility and quality manufacturing have substantial effects in the results.
According to Oblique line test, controlling variation would help to reduce errors and controlling errors sources. In addition, human's fluctuation error and joints flexibility are effective factors on manipulator accuracy. Maximum dynamic load carrying capacity would be attained in experience in different trajectories with different loads and Rp quantity. While in Rp =0.08m, the maximum load is 15Kg in comparison with 10Kg for simulation maximum load with the same Rp; the manipulator does not have actuator so talking about torque is meaningless. According to RD's petrol tank weight, 10Kg, the result is acceptable.
XIII. CONCLUSION
The manipulator is designed, simulated and tested in different trajectories and pose. While the manipulator is designed to carrying the automobile petrol tank, operator's facility, end-effector speed, accuracy and DLCC are the main criteria. The main error sources are human's fluctuation, noise, measurement tools etc. although the experimental results are near the theoretical ones, at the end of trajectory, according to joint flexibility and non-accurate manufacturing they diverge, and the error interval is about 5-8 percent. Quality manufacturing, manipulator conditions, adaptable working space and optimizing the pneumatic system design are main criteria in manipulator manufacturing. According to manipulator usage, maximum error in each trajectory, pose accuracy and pose repeatability are its important characteristics. Regarding error sources, as human's fluctuation in automobile petrol tank carrying, deviation from desired path particularly in direct angular rotation of the joints, is acceptable.
REFERENCES
1. Gamarraado, V.O. and E.A.O. Yuhara, "Dynamics modeling and simulation of flexible robotic manipulator," Robotica, 17, 523-528 (1999). [ Links ]
2. Ider, S.K. and M.K. Ozgoren, "Trajectory tracking control of flexible joint robots," Computers and structures, 76, 757-763 (2000). [ Links ]
3. Korayem, M.H. and A. Basu, "Formulation and numerical solution of elastic robot dynamic motion with maximum load carrying capacities," Robotica, 12, 253-261 (1994a). [ Links ]
4. Korayem, M.H. and A. Basu, "Dynamic load carrying capacity for robotic manipulators with joint elasticity imposing accuracy constraints," Robot Auton. Sys, 13, 219-229 (1994b). [ Links ]
5. Korayem, M.H. and H. Ghariblu, "Maximum allowable load on wheeled mobile manipulators imposing redundancy constraints," Robot Auton. Sys, 44, 151-159 (2003). [ Links ]
6. Korayem, M.H. and M. Shokri, "Maximum dynamic load carrying capacity of 6UPS-Stewart platform flexible joint manipulator," IEEE Int. Conf. on Robotics and Biomimetics, Kunming, China, 727-732 (2006). [ Links ]
7. Korayem, M.H., A. Heidari, A. Nikoobin, "Maximum allowable dynamic load of flexible mobile manipulators using finite element approach," Int. J Adv Manufacture and Technology, 36, 606-617 (2008). [ Links ]
8. Rivin, E., Mechanical design of robots, McGraw-Hill, New York (1988). [ Links ]
9. Sweet, L.M. and M.C. Good, "Redefinition of the robot motion control problem," IEEE Control Syst., 5, 18-24 (1985). [ Links ]
10. Thomas, M., H.C. Yuan-Chou and D. Tesar, "Optimal actuator sizing for robotic manipulators based on local dynamic criteria," ASME Journal of Mechanisms, Transactions and Automation Design, 107, 163-169 (1985). [ Links ]
11. Wang, L.T. and B. Ravani, "Dynamic load carrying capacity of mechanical manipulators -Part I: Problem formulation," Transactions of ASME Journal of Dynamic System, Measurement and Control, 110, 46-52 (1988). [ Links ]
12. Yue, Sh. and S.K. Tso, "Maximum dynamic payload trajectory for flexible robot manipulators with kinematic redundancy," Mechanism and Machine Theory, 36, 785- 800 (2001). [ Links ]
Received: July 19, 2009.
Accepted: April 5, 2010.
Recommended by Subject Editor Jorge Solsona.














