Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. vol.41 no.2 Bahía Blanca abr. 2011
ARTICLES
Thermal diffusion effect on a three-dimensional mhd free convection with mass transfer flow from a porous vertical plate
N. Ahmed, H. K. Sarmah and D. Kalita
Department of Mathematics. Gauhati University, Guwahati 781 014. Assam, India
e-mail: saheel_nazib@yahoo.com
Abstract - A systematic analysis to study the effect of thermal diffusion on a three dimensional free convective flow with mass transfer of an incompressible viscous electrically conducting fluid past a porous vertical plate with transverse sinusoidal suction velocity is presented. Due to this type of suction velocity at the plate the flow becomes three-dimensional one. A magnetic field of uniform strength is assumed to be applied normal to the plate directed into the fluid region. The magnetic Reynolds number is considered to be small so that the induced magnetic field can be neglected. An analytical solution of the problem is obtained. The expressions for the velocity field, fluid temperature, species concentration, fluid pressure, skin-friction, Nusselt number and Sherwood number and current density are obtained in non-dimensional forms. The effects of Hartmann number, Soret number, Reynolds number and Prandtl number on the velocity field, temperature and concentration distributions, skin friction at the plate and on the amplitudes of the first order skin-friction, the first order Nusselt number and the first order Sherwood number at the plate are discussed graphically. It is seen that the thermal diffusion and applied magnetic field have significant effects on the flow and on the heat and mass transfer characteristics.
Keywords - Thermal Diffusion; Species Concentration; Free Convection; Skin-Friction; Electrically Conducting.
I. INTRODUCTION
Many natural phenomena and technological problems are susceptible to MHD analysis. Geophysics encounters MHD characteristics in the interactions of conducting fluids and magnetic fields. Engineers employ MHD principle in the design of heat exchange pumps and flow meters, in space vehicle propulsion, thermal protection, braking, control and re-entry, in creating naval power generating systems etc. From technological point of view, MHD convection flow problems are also very significant in the fields of stellar and planetary magnetospheres, aeronautics, chemical engineering and electronics. The application of MHD principles in medicine and biology are of paramount interest owing to their significance in bio medical engineering in general and in the treatment of various pathological state in particular. Applications in biomedical engineering include cardiac MRI, ECG etc. MHD is also used in stabilizing a flow against the transition from laminar to turbulent flow and in the reduction of turbulent drag and suppression of flow separation. Some Model studies of the above phenomena of MHD convection have been made by many. Some of them are Sanyal and Bhattacharya (1992), Ferraro and Plumpton (1996) and Cramer and Pai (1973). On the other hand, along with free convection currents caused by the temperature difference, the flow is also affected by the difference in concentrations of material constitutions. Many investigators have studied the phenomena of MHD free convection and mass transfer flow of who the names of Singh and Singh (2000) and Singh et al. (2007) are worth mentioning.
The effect of the three dimensional flow caused by the periodic suction perpendicular to the main flow when the difference between the wall temperature and free stream temperature gives rise to buoyancy force in the direction of the free stream on heat transfer characteristics was investigated by Singh et al. (1988), Ahmed and Sarma (1997) and Chaudhary and Chand (2002). The effects of transverse sinusoidal injection velocity distribution on the three dimensional free convective Couette flow of a viscous incompressible fluid in slip flow regime under the influence of heat source has been recently studied by Jain and Gupta (2006). Ahmed et al. (2006) obtained an analytical solution to the problem of the three-dimensional free convective flow of an incompressible viscous fluid past a porous vertical plate with transverse sinusoidal suction velocity taking into account the presence of species concentration.
However in the above mentioned works, the thermal - diffusion (Soret) effect was not taken into account. This assumption is justified when the concentration level is very low. The flux of mass caused due to temperature gradient is known as the Soret effect or the thermal - diffusion effect. The thermal diffusion effect is applied for isotope separation and in mixtures between gases with very light molecular weight (H2,He) and medium molecular weight (N2,air) where the diffusion - thermo effect is found to be of a magnitude such that it can not be neglected. The experimental investigation of the thermal - diffusion effect on mass transfer related problem was first performed by Charles Soret in 1879. There after this thermal - diffusion effect is termed as the Soret effect in honour of Charles Soret. In general the Soret effect is of a smaller order of magnitude than the effect described in Fick's law and very often it is neglected in mass transfer process. Though this effect is quite small, but the devices can be arranged to produce very steep temperature gradient so that the separation of components in mixtures is affected. Eckert and Drake (1972) have emphasized the importance of the Soret effect in the cases concerning isotope separation and in mixtures between gases with very light molecular weight (H2,He) and for medium molecular weight (N2,air). Following Eckert and Drake (1972) work several other investigators have carried out model studies on the Soret and Dufour effects in different heat and mass transfer problems. Some of them are Hurle and Jakeman (1971), Sattar and Alam (1994), Singh et al. (2007) and Raju et al. (2008).
In view of the importance of the joint effect of the magnetic field and thermal diffusion, it is proposed to study a problem of three dimensional MHD free convective flow with mass transfer past a porous vertical infinite plate taking into account the effect of thermal diffusion. The infinite plate assumption is one such classical idealization of great practical importance. Although the flow over a flat plate is the simplest case of boundary layer development in external flow, yet its significance cannot be undervalued because of its relevance to numerous engineering applications. Several configurations such as flow over airfoils, turbine blades, ship hulls etc. can initially be estimated as flow past flat plates. The justification of considering the three-dimensional flow is that most of the fluid flows that occur in nature are three-dimensional. Of course we have chosen a simple model of a three-dimensional flow caused by transverse sinusoidal suction velocity. Here, our main objectives are to study the Soret effect and the magnetic field effect on the flow and heat and mass transfer characteristics.
II. BASIC EQUATIONS
The equations governing the steady motion of an incompressible viscous electrically conducting fluid in presence of a magnetic field are
The continuity equation (Ferraro and Plumpton, 1966)
 | (1) |
The Gauss's law of magnetism (Ferraro and Plumpton, 1966)
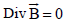 | (2) |
The momentum equation (Ferraro and Plumpton, 1966)
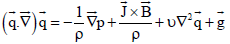 | (3) |
The energy equation (Eckert and Drake, 1972; Ferraro and Plumpton, 1966)
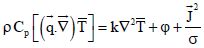 | (4) |
The species continuity equation (Eckert and Drake, 1972)
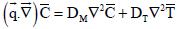 | (5) |
The Ohm's law (Ferraro and Plumpton, 1966)
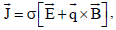 | (6) |
where, 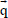 is the fluid velocity vector, p is the pressure,
is the fluid velocity vector, p is the pressure, 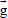 is the acceleration due to gravity, υ is the kinematic viscosity,
is the acceleration due to gravity, υ is the kinematic viscosity,  is the temperature,
is the temperature,  is the magnetic induction vector,
is the magnetic induction vector, 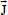 is the electric current density,
is the electric current density, 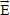 is the electric field, (here assumed to be Zero) σ is the electrical conductivity, k is the thermal conductivity, φ is the viscous dissipation of energy per unit volume, Cp is the specific heat at constant pressure, ρ is the density of the fluid,
is the electric field, (here assumed to be Zero) σ is the electrical conductivity, k is the thermal conductivity, φ is the viscous dissipation of energy per unit volume, Cp is the specific heat at constant pressure, ρ is the density of the fluid, 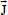 ×
×  is the Lorentz force per unit volume,
is the Lorentz force per unit volume, 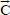 is the species concentration, DM is the co-efficient of chemical molecular diffusivity, DT is the co-efficient of chemical thermal diffusivity and the other symbols have their usual meanings.
is the species concentration, DM is the co-efficient of chemical molecular diffusivity, DT is the co-efficient of chemical thermal diffusivity and the other symbols have their usual meanings.
We now consider the steady free convection flow of an incompressible viscous electrically conducting fluid taking into account species concentration and thermal diffusion past a vertical porous plate with transverse sinusoidal suction velocity by making the following assumptions
(i) All the fluid properties except the density in the buoyancy force term are constants.
(ii) A magnetic field of uniform strength Bo is applied normal to the plate directed into the fluid region.
(iii) The magnetic Reynolds number is so small that the induced magnetic fluid can be neglected.
(iv) The viscous dissipation and magnetic dissipations of energy are negligible.
(v) 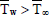 and
and 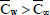
We introduce a co-ordinate system 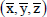 with X-axis vertically upwards along the plate, Y-axis perpendicular to it and directed into the fluid region and Z-axis along the width of the plate.
with X-axis vertically upwards along the plate, Y-axis perpendicular to it and directed into the fluid region and Z-axis along the width of the plate.
Let 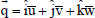 be the fluid velocity at the point
be the fluid velocity at the point 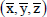 and
and 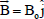 be the applied magnetic field,
be the applied magnetic field, 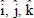 being the unit vectors along X-axis, Y-axis and Z-axis respectively.
being the unit vectors along X-axis, Y-axis and Z-axis respectively.
The suction velocity is taken as follows:
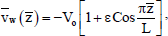 | (7) |
where ε is small reference parameter such that ε << 1 and L is the wavelength of the periodic suction. Since the plate is infinite in length in X-direction, therefore all the quantities except possibly the pressure are assumed to be independent of  .
.
With the foregoing assumptions and under the usual boundary layer and Boussinesq approximation (Eckert and Drake, 1972), the Eqs. (1), (2), (4) and (5) reduce to
Continuity equation:
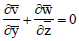 | (8) |
Momentum equations:
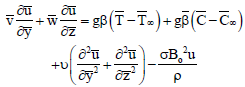 | (9) |
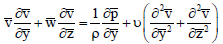 | (10) |
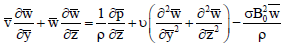 | (11) |
Energy equation:
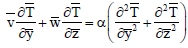 | (12) |
Species continuity equation:
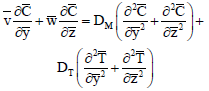 | (13) |
where, β is the coefficient of volume expansion for heat transfer, 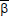 is the coefficient of volume expansion for mass transfer, α is the thermal diffusivity,
is the coefficient of volume expansion for mass transfer, α is the thermal diffusivity, 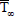 is the fluid temperature in the free stream,
is the fluid temperature in the free stream, 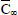 is the species concentration in the free stream and the other symbols have their usual meanings.
is the species concentration in the free stream and the other symbols have their usual meanings.
The Eq. (2) is satisfied by 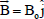 .
.
The relevant boundary conditions are
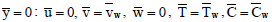 | (14) |
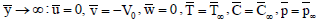 | (15) |
We introduce the following dimensionless quantities:
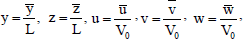
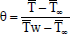 (Dimensionless temperature),
(Dimensionless temperature), 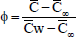 (Dimensionless species concentration),
(Dimensionless species concentration), (Prandtl number),
(Prandtl number), 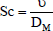 (Schmidt number),
(Schmidt number), 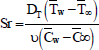 (Soret number),
(Soret number), 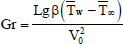 (Grashof number for heat transfer),
(Grashof number for heat transfer), 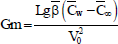 (Grashof number for mass transfer),
(Grashof number for mass transfer),  (Hartmann number),
(Hartmann number), 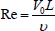 (Reynolds number),
(Reynolds number), 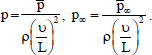
The non-dimensional forms of the Eqs. (8-13) are
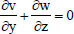 | (16) |
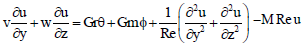 | (17) |
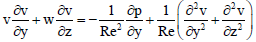 | (18) |
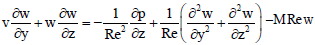 | (19) |
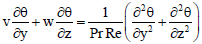 | (20) |
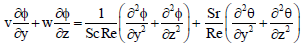 | (21) |
With relevant boundary conditions:
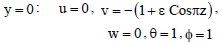 | (22) |
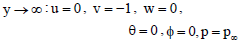 | (23) |
III. METHOD OF SOLUTION
We assume the solutions of the Eqs (16) to (21) to be of the form:
u = u0(y) + εu1(y,z) + 0(ε2) (24)
v = v0(y) + εv1(y,z) + 0(ε2) (25)
w = w0(y) + εw1(y,z) + 0(ε2) (26)
p = p0(y) + εp1(y,z) + 0(ε2) (27)
θ = θ0(y) + εθ1(y,z) + 0(ε2) (28)
 =
=  0(y) + ε
0(y) + ε 1(y,z) + 0(ε2) (29)
1(y,z) + 0(ε2) (29)
with p0 = p∞, w0 = 0.
Substituting these in the Eqs. (16-21) and by equating the coefficients of the similar terms and neglecting ε2, the following differential equations are obtained.
Zeroth - Order equations:
 | (30) |
 | (31) |
 | (32) |
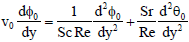 | (33) |
First order equations:
 | (34) |
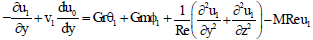 | (35) |
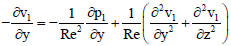 | (36) |
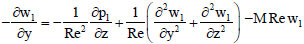 | (37) |
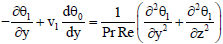 | (38) |
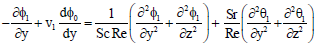 | (39) |
Subject to the boundary conditions
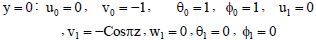 | (40) |
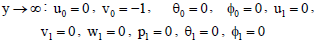 | (41) |
The solution of the Eqs. (33-33) under the boundary conditions (40) and (41) are
| v0 = -1 | (42) |
| θ0 = e-Pr Re y | (43) |
 0 = (1-a)e-Sc Re y + ae-Pr Re y for Sc ≠ Pr 0 = (1-a)e-Sc Re y + ae-Pr Re y for Sc ≠ Pr | (44) |
| = (1 + Pr2 Sr Re y)e-Pr Re y for Sc = Pr | (45) |
| u0 = A1e-Pr Re y + A2e-Sc Re y + (-A1 -A2)e-λ Re y for Sc ≠ Pr | (46) |
| = A6(e-λ Re y - e-Pr Re y) - A5ue-Pe Re y for Sc = Pr | (47) |
| where, | |
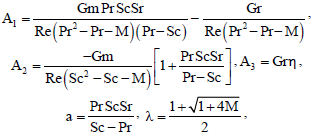 | |
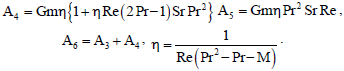 | |
IV. CROSS FLOW SOLUTION:
We shall first consider the Eqs. (34), (36), (37) for v1(y,z), w1(y,z) and p1(y,z) which are independent of the main flow component u1, temperature field θ1 and the concentration field  1.
1.
The suction velocity vw = -(1 + εCosπz) consists of a basic uniform distribution -1 with superimposed weak sinusoidal distribution εCosπz. Hence the velocity components v, w and p are also separated into mean and small sinusoidal components v1, w1 and p1.
We assume v1, w1 and p1 to be of the following forms:
| v1 = -πv11(y)Cosπz | (48) |
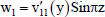 | (49) |
| p1 = Re2p11(y)Cosπz. | (50) |
On substitution of (48), (49) and (50), Eq (34) is satisfied and Eqs. (36) and (37) reduce to the following ordinary differential equations:
 | (51) |
 | (52) |
with relevant boundary conditions
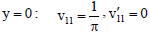 | (53) |
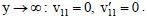 | (54) |
The solutions of these equations are:
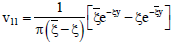 | (55) |
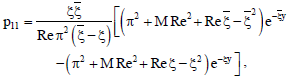 | (56) |
where 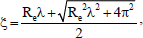
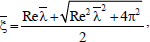
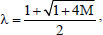

Hence the solutions for the velocity components v1, w1 and pressure p1 and as follows
 | (57) |
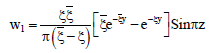 | (58) |
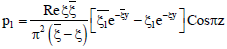 | (59) |
where
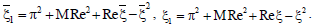
V. SOLUTION FOR FIRST ORDER FLOW, CONCENTRATION AND TEMPERATURE FIELD
We now consider the Eqs. (35), (38) and (39). The solutions for velocity components u1, temperature field θ and concentration field  are also separated into mean and sinusoidal components u1, θ1 and
are also separated into mean and sinusoidal components u1, θ1 and  1. To reduce the partial differential Eqs. (35), (38), (39) into ordinary differential equations, we consider the following forms for u1, θ1 and
1. To reduce the partial differential Eqs. (35), (38), (39) into ordinary differential equations, we consider the following forms for u1, θ1 and  1.
1.
u1 = u11(y)Cosπz (60)
θ1 = θ11(y)Cosπz (61)
u1 = u11(y)Cosπz (62).
Using the expressions for u1, v1, θ1,  1 in (35), (38) and (39), we get the following ordinary differential equations
1 in (35), (38) and (39), we get the following ordinary differential equations
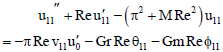 | (63) |
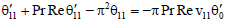 | (64) |
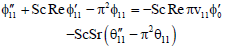 | (65) |
with the boundary conditions
y = 0: u11 = 0, θ11 = 0,  11 = 0 (66)
11 = 0 (66)
y → ∞: u11 = 0, θ11 = 0,  11 = 0 (67)
11 = 0 (67)
The solutions of the Eqs. (63), (64) and (65) subject to the boundary conditions (66) and (67) are
 | (68) |
 | (69) |
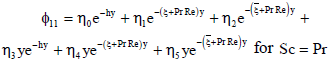 | (70) |
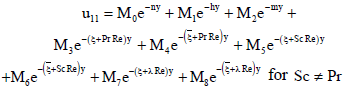 | (71) |
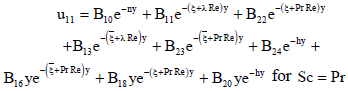 | (72) |
where
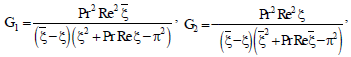
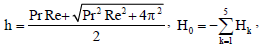
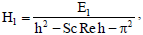
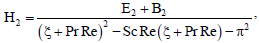
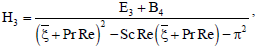
G0 = -(G1 + G2)

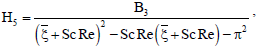

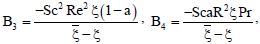
E2 = -ScSr{G1(ξ + Pr Re)2 - π2G1},
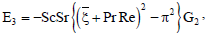
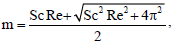

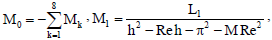
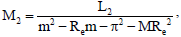
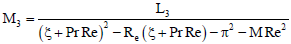
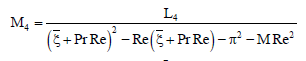
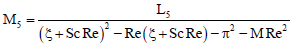
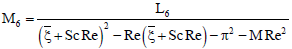


L1 = -GrReG0 - GmReH1, L2 = -GmReH0,
L3 = K1 - GmReH2 - GrReG1,
L4 = K4 - GrReH3, L5 = K2 - GmReH4,

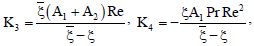

η0 = - (η1 + η2), η1 = C2 + η4J1, η2 = C3 + η5J2,
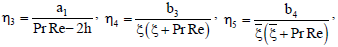
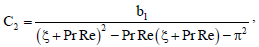


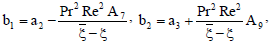

a1 = - PrSr(h2 - π2)G0,
a2 = - PrSrG1 {(ξ + PrRe)2 - π2},
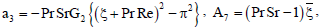
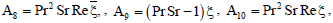
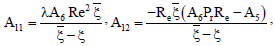
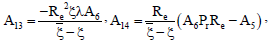
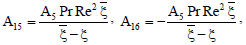
A17 = A12 - GrReG1 - GmReη1,
A18 = A14 - GrReG2 - GmReη2,
A19 = A15 - η5.GmRe, A20 = A16 - η4GmRe
A21 = GrReG0 - GmReη0, A22 = - GmReη3,
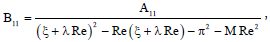
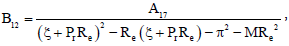

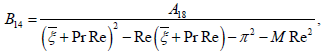

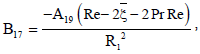
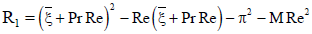
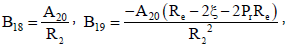
R2 = (ξ + PrRe)2 - Re(ξ + PrRe) - π2 - MRe2

R3 = h2 - Reh - π2 - MRe2, B22 = B12 + B19
B23 = B14 + B17, B24 = B25 + B21,
B10 = -(B11 + B22 + B13 + B23 + B24 + B20)
The dimensionless velocity fields u, v, w; the pressure distribution p, the temperature field θ and the concentration field  are as follows:
are as follows:
| u = u0(y) + εu11(y)Cosπz + 0(ε2) | (73) |
| v = v0(y) - εv11(y)Cosπz + 0(ε2) | (74) |
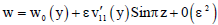 | (75) |
| p = p0(y) + εRe2p11(y)Cosπz + 0(ε2) | (76) |
| θ = θ0(y) + εθ11(y)Cosπz + 0(ε2) | (77) |
 = =  0(y) + ε 0(y) + ε 11(y)osπz + 0(ε2) 11(y)osπz + 0(ε2) | (78) |
with p0 = p∞, w0 = 0.
VI. SKIN-FRICTION AT THE PLATE
The non-dimensional skin-friction at the plate in the direction of the free stream is given by -
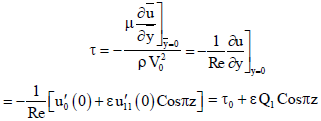 | (79). |
where,
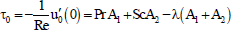 | for Pr ≠ Sc (80) | |
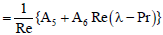 | for Pr = Sc | (81) |
and
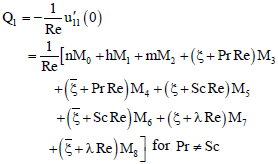 | (82) |
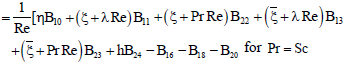 | (83) |
VII. THE CO-EFFICIENT OF RATE OF HEAT TRANSFER
The heat flux from the plate to the fluid in terms of Nusselt number Nu is given by
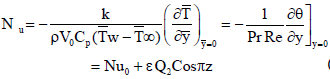 | (84) |
where, 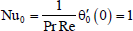 and
and
 | (85) |
VIII. THE CO-EFFICIENT OF MASS TRANSFER:
The mass flux at the wall y=0 in terms of Sherwood number Sh is given by
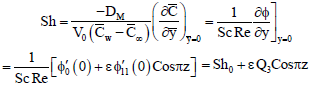 | (86) |
where,
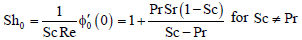 | (87) |
| = 1 - PrSr for Sc = Pr | (88) |
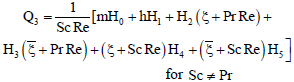 | (89) |
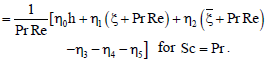 | (90) |
IX. CURRENT DENSITY
The current density 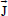 is given by
is given by
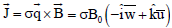 | (91) |
The magnitude of 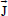 is given by
is given by
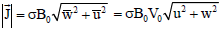 | (92) |
The current density (in magnitude) in non-dimensional form is given by

That is the magnitude of the non-dimensional current density is proportional to the boundary layer velocity.
X. RESULTS AND DISCUSSION.
In order to get physical insight into the problem, we have carried out the numerical calculations for u, θ,  , Q1, Q2, Q3 and τ which are respectively the velocity component in main flow direction, fluid temperature, species concentration, amplitudes of the first order skin friction, Nusselt number, Sherwood number and skin friction at the plate y=0 in direction of the buoyancy force and their values are demonstrated in graphs. It may be noted that Q1, Q2 and Q3 may be termed as the first order skin friction, Nusselt number and Sherwood number at the plate y=0 for z=0. In other words Q1, Q2 and Q3 are respectively the maximum first order skin friction, Nusselt number and Sherwood number at the plate y=0 .We have restricted our investigation to Pr (Prandtl number) equal to 0.7 which corresponds to air. The value of the Grashof number Gr for heat transfer has been chosen as 10 (externally cooled plate) whereas the value of Grashof number Gm for mass transfer is kept fixed at 5 .As we have considered water vapour as solute and air as solvent, therefore the value of the Schmidt number Sc is chosen as 0.60. The value of the Soret number Sr, the Hartmann number M and the Reynolds number Re are taken arbitrarily.
, Q1, Q2, Q3 and τ which are respectively the velocity component in main flow direction, fluid temperature, species concentration, amplitudes of the first order skin friction, Nusselt number, Sherwood number and skin friction at the plate y=0 in direction of the buoyancy force and their values are demonstrated in graphs. It may be noted that Q1, Q2 and Q3 may be termed as the first order skin friction, Nusselt number and Sherwood number at the plate y=0 for z=0. In other words Q1, Q2 and Q3 are respectively the maximum first order skin friction, Nusselt number and Sherwood number at the plate y=0 .We have restricted our investigation to Pr (Prandtl number) equal to 0.7 which corresponds to air. The value of the Grashof number Gr for heat transfer has been chosen as 10 (externally cooled plate) whereas the value of Grashof number Gm for mass transfer is kept fixed at 5 .As we have considered water vapour as solute and air as solvent, therefore the value of the Schmidt number Sc is chosen as 0.60. The value of the Soret number Sr, the Hartmann number M and the Reynolds number Re are taken arbitrarily.
The variation of the velocity field u against y under the influence of Re, M and Sr has been displayed in Figs. 2-4. It is inferred from these figures that the thermal diffusion effect accelerates the flow whereas an increase in the Hartmann number or the Reynolds number causes the fluid velocity to fall. That is the flow is retarded due to the application of the transverse magnetic field. The same figures further indicate that the fluid velocity first increases in a very thin layer adjacent to the plate and after this layer the fluid velocity asymptotically decreases to its zero value as y → ∞.
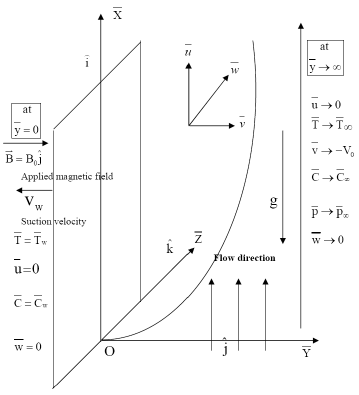
Fig 1. The flow configuration
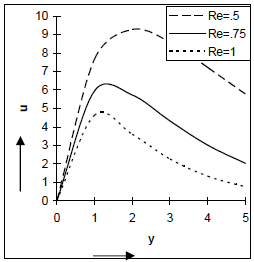
Fig 2: velocity distribution u versus y when Pr=. 71, Sc=. 6, Gr=10, Gm=5, M=1,Sr=1, ε=.001, z=1/6.

Fig 3: velocity distribution u versus y when Pr=. 71, Sc=. 6, Gr=10, Gm=5, M=1, Re=.5, ε=.001, z=1/6.
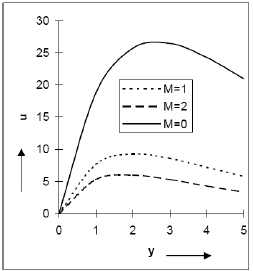
Fig 4: velocity distribution u versus y when Pr=. 71, Sc=. 6, Gr=10, Gm=5, Sr=1, Re=.5, ε=.001, z=1/6.
Figure 5 depicts the change of behaviour of the temperature versus y under the effect of the Reynolds number. This figure clearly shows that an increase in the Reynolds number Re leads the fluid temperature to fall. That is the fluid temperature is kept low due to suction (large Reynolds number). There is also a clear indication from this figure that the fluid temperature asymptotically falls from its maximum value to minimum value as y → ∞
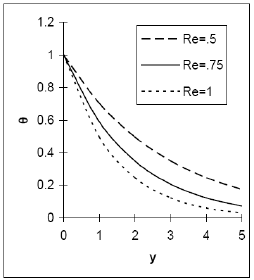
Fig 5: velocity distribution u versus y when Pr=. 71, Sc=. 6, Gr=10, Gm=5, M=1, Sr=1, ε=. 001, z=1/6.
The effects of the Reynolds number Re, Soret number Sr and the normal coordinate y on the concentration  are presented in Fig. 6 and Fig. 7. It is observed from these figures that a steady drop in the concentration occurs when the Reynolds number Re is increased or the Soret number Sr is decreased. In other words the thermal diffusion raises the concentration whereas the suction velocity leads to a steady fall in
are presented in Fig. 6 and Fig. 7. It is observed from these figures that a steady drop in the concentration occurs when the Reynolds number Re is increased or the Soret number Sr is decreased. In other words the thermal diffusion raises the concentration whereas the suction velocity leads to a steady fall in  . Further it is noticed from these figures that for small Soret number Sr, as the distance of the fluid particles increases the concentration decreases. But for large Soret number
. Further it is noticed from these figures that for small Soret number Sr, as the distance of the fluid particles increases the concentration decreases. But for large Soret number  first increases in a thin layer adjacent to the plate and there after it falls down.
first increases in a thin layer adjacent to the plate and there after it falls down.
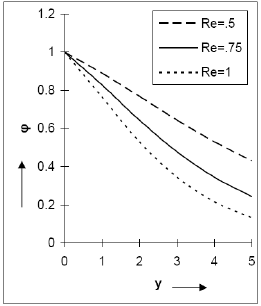
Fig 6: Species concentration distribution φ versus y when Pr=. 71, Sc=. 6, Gr=10, Gm=5, M=1, Sr=1, ε=.001, z=1/6.
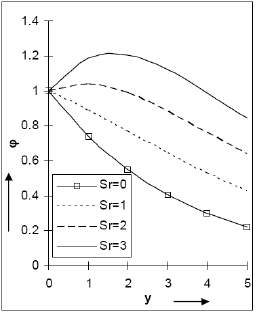
Fig 7: Species concentration distribution φ versus y when Pr=. 71, Sc=. 6, Gr=10, Gm=5, M=1, Re=.5, ε=.001, z=1/6.
The influence of the Reynolds number Re, thermal diffusion and the magnetic field on Q1 (first order skin-friction) are presented in the Figs. 8 and 9. It is seen that the Soret effect or the imposition of the magnetic field and suction leads Q1 to decrease. That is the first order viscous drag on the plate is reduced under thermal diffusion or due to the application of the transverse magnetic field or suction on the plate.

Fig 8: The amplitude Q1 for the first order skin friction for Pr=. 71, Sc=. 6, Gr=10, Gm=5, M=1against Reynolds number Re
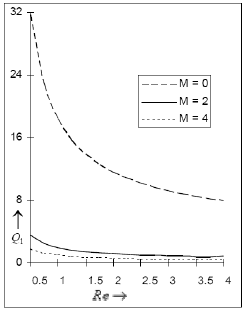
Fig 9: The amplitude Q1 for the first order skin friction for Pr=. 71, Sc=. 6, Gr=10, Gm=5, Sr=1against Reynolds number Re
Figures 10 and 11 exhibit the influence of the Reynolds number, Soret number and the magnetic field parameter on Q2 (first order Nusselt number). It is observed from these figures that the Soret effect is insignificant on Q2 although an increase in magnetic field parameter as well as the Reynolds number causes a growth in Q2.
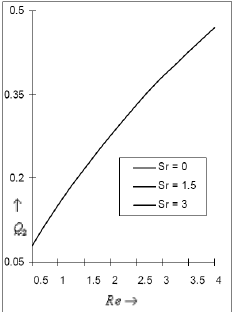
Fig 10: The amplitude Q2 for the first order skin friction for Pr=. 71, Sc=. 6, Gr=10, Gm=5, M=1against Reynolds number Re
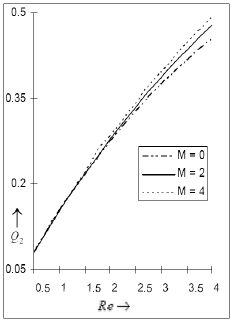
Fig 11: The amplitude Q2 for the first order skin friction for Pr=. 71, Sc=. 6, Gr=10, Gm=5, S r=1against Reynolds number Re
The behavior of Q3 (first order Sherwood number) under the effect of thermal diffusion, magnetic field and the Reynolds number is demonstrated in the Figs. 12 and 13. We observe that the Soret effect leads to a growth in Q3. Again, in the absence of a magnetic field Q3 is positive i.e. the first order mass flux occurs from the plate to the fluid whereas this behavior takes reverse trend in the presence of a magnetic field. Hence, in the presence of a magnetic field, the first order mass flux occurs from the fluid to the plate. Moreover, the imposition of the magnetic field leads the magnitude of first order mass flux at the plate to fall.

Fig 12: The amplitude Q3 for the first order skin friction for Pr=.71, Sc=.6, Gr=10, Gm=5, M=1 against Reynolds number Re
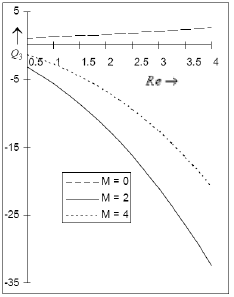
Fig 13: The amplitude Q3 for the first order skin friction for Pr=. 71, Sc=. 6, Gr=10, Gm=5, Sr=1against Reynolds number Re
The nature of skin friction τ at the plate in the direction of the buoyancy force versus Reynolds number, Hartmann number and Soret number is depicted in the Figs. 14 and 15. It is seen that the application of the magnetic field and suction reduces the viscous drag at the plate surface whereas the thermal diffusion effect results in a moderate growth in the skin friction.
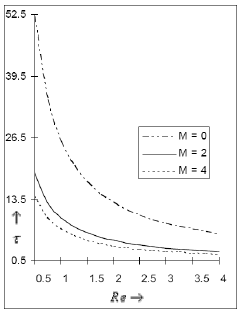
Fig 14: The skin friction τ for Pr=. 71, Sc=.6, Gr=10, Gm=5, Sr=1against Reynolds number Re
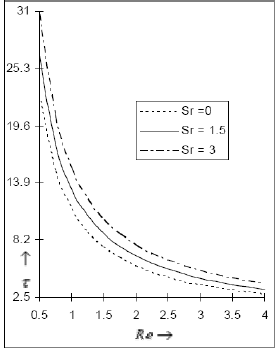
Fig 15: The skin friction τ for Pr=. 71, Sc=. 6, Gr=10, Gm=5, M=1against Reynolds number Re
XI. CONCLUSIONS
Our investigation leads to the following conclusions.
1. The flow is retarded due to the application of the transverse magnetic field and suction.
2. The fluid temperature is kept low due to suction (large Reynolds number).
3. The thermal diffusion raises the concentration whereas the suction velocity leads to a steady fall in the concentration  .
.
4. The first order viscous drag on the plate is reduced under thermal diffusion or due to the application of the transverse magnetic field or suction on the plate.
5. It is observed from these figures that the Soret effect is insignificant on Q2 (first order Nusselt number) although an increase in magnetic field parameter as well as the Reynolds number causes a growth in Q2.
6. The Soret effect leads to a growth in Q3 (first order Sherwood number). In the absence of a magnetic field the first order mass flux occurs from the plate to the fluid whereas this behavior takes reverse trend in the presence of a magnetic field.. Moreover, the imposition of the magnetic field leads the magnitude of first order mass flux at the plate to fall.
7. The application of the magnetic field and suction reduces the viscous drag at the plate surface whereas the thermal diffusion effect results in a moderate growth in the skin friction.
ACKNOWLEDGEMENT
The Authors of the paper are highly thankful to UGC for supporting the research work under MRP (F. No. 36-96/2008(SR))
REFERENCES
1. Ahmed, N. and D. Sarma, "Three-dimensional free convection flow and heat transfer through a porous medium," Indian J. Pure Appl. Math, 26, 1345-1353 (1997). [ Links ]
2. Ahmed, N., D. Sarma and D.P. Barua, "Three dimensional free convective flow and mass transfer along a porous vertical plate," Bulletin of the Allahabad Mathematical Society, 21, 128-141 (2006). [ Links ]
3. Cramer, K.P. and S.I. Pai, Magneto Fluid Dynamics for Engineers and Applied Physics, New York: McGraw-Hill Book Co (1973). [ Links ]
4. Chaudhary, R.C. and T. Chand, "Three-dimensional flow and heat transfer through porous medium," Int. J. Appl. Mech. Engineering, 7, 1141-1156 (2002). [ Links ]
5. Eckert, E.R.G. and R.M. Drake, Analysis of Heat and Mass Transfer, New York: McGraw-Hill (1972). [ Links ]
6. Ferraro, V.C.A and C. Plumpton, An introduction to Magneto Fluid Mechanics, Oxford, Clarendon Press (1966). [ Links ]
7. Hurle, D.T.J. and E Jakeman, "Soret-Driven Thermosolutal Convection," J. Fluid Mechanics, 47,667-687 (1971). [ Links ]
8. Jain, N.C and P. Gupta, "Three-dimensional free convection couette flow with transpiration cooling," Journal of Zhejiang University Science A, 7, 340-346 (2006). [ Links ]
9. Raju, M.C., S.V.K. Varma, P.V. Reddy and S. Saha, "Soret effects due to natural convection between heated inclined plates with magnetic field," Journal of Mechanical Engineering, 39,65-70 (2008). [ Links ]
10. Sanyal, D.C and S. Bhattacharya, "Similarly solutions of an unsteady incompressible thermal MHD boundary layer flow by group theoretic approach," In. J. Eng. Sci., 30, 561-569 (1992). [ Links ]
11. Sattar, M.A. and M.M. Alam, "Thermal-diffusion as well as transpiration effects on MHD free convection and mass transfer flow past an accelerated vertical porous plate," Indian J. Pure, Appl. Math., 25, 679-688 (1994). [ Links ]
12. Singh, N.P. and A. Kr. Singh, "MHD effects on Heat and mass transfer in flow of a viscous fluid with induced magnetic field," Ind. J. Pure Appl. Phys., 38, 182-189 (2000). [ Links ]
13. Singh, N.P., A.Kr. Singh and and Kr. Ajay, "MHD free convection MHD mass transfer flow part of flat plate," The Arabian Journal for Science and Engineering, 32, 93-112 (2007). [ Links ]
14. Singh, P., J.K. Mishra and K.A. Narayan, "Three-dimensional convective flow and heat transfer in a porous medium," Indian J. Pure Appl. Math., 19, 1130-1135 (1988). [ Links ]
Received: July 8, 2009.
Accepted: April 14, 2010.
Recommended by Subject Editor Walter Ambrosini.














