Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. vol.41 no.2 Bahía Blanca abr. 2011
ARTICLES
Modeling conventional one-dimensional drying of radiata pine based on the effective diffusion coefficient
Y.A. Gatica, C. H. Salinas and R.A. Ananias*
Doctoral student in Wood Sciences and Industries, U. del Bío-Bío, Collao 1202, Concepción, CHILE.
ygatica@ubiobio.cl
Department of Mechanical Engineering, U. del Bío-Bío, Collao 1202,Concepción CHILE.
casali@ubiobio.cl
* Department of Wood Engineering, U. del Bío-Bío, Collao 1202, Concepción, CHILE.
ananias@ubiobio.cl
Abstract - We modeled conventional one-dimensional drying of radiata pine (Pinus radiata) wood using the concept of effective diffusion. The experimentally determined effective diffusion coefficients for the radial and tangential directions were related exponentially to the moisture content. These coefficients were characterized by two parameters that were determined through optimization within the context of an inverse problem. One-dimensional drying experiments were carried out under constant drying 44/36 (°C/°C) in order to determine transitory spatial distributions of moisture and drying curves, which were used then to determine the model parameters and validate the model. The mathematical model consisted of a partial, non-linear, differential equation of the second order and was characterized by coefficients that varied exponentially with moisture content; this later was integrated numerically through the finite volume method. Simulations of the transitory distribution of moisture gradients gave satisfactory results, and the drying curves were correlated with experimental data as well as the values of the parameters required by the proposed model.
Keywords - Drying; Wood; Radiata Pine; Diffusion.
I. INTRODUCTION
The process of drying wood is particularly interesting due to the complexity of this material's porous matrix and the different form in which water can be found within it (free water in cavities of the porous matrix, water contained within cell walls). This complexity leads to diverse physical mechanisms of moisture transport (capillary flow, convection, diffusion) and is heightened by the high variability among species as well as differences resulting from the tree age, height of the cut, growing conditions, etc.
The modeling of moisture transport in wood can be viewed from a phenomenological point of view or in terms of the physics of the transport phenomena (Ananias et al., 2005; Salinas et al., 2008). The latter approach includes classical diffusion models such as those presented by Stamm (1964) or Siau (1984), models based on the thermodynamics of irreversible processes (Luikov, 1966), and those developed using Whittaker's multiphase approach (Whittaker, 1977).
This study focuses on diffusion models, which are advantageous given their simplicity in terms of the number of physical parameters required and numerical calculations. Wood drying simulations of conifers below the fiber saturation point (FSP) traditionally rely on these methods due to the dominance of diffusive transport in this range (Smith and Langrish, 2008; Hukka, 1999; Pang, 1997). When wood exceeds the FSP, diffusion models are limited by other dominant phenomena such as capillarity and permeability (Keey et al., 2000). By the way, the researchers have formulated models that made difference above and below FSP like the one proposed by Davis et al. (2002). Nonetheless, diffusion models have also been used beyond the hygroscopic range; these use an effective water diffusion coefficient obtained as suggested for porous materials in general by Chen (2007) and employed to simulate the drying kinetics across the entire moisture range of conifer woods by Rozas et al. (2009). In this matter, we followed the suggestion of Hukka (1999), who simulated moisture transport in the transversal plane of Scots pine (Pinus sylvestris) based on the concept of an effective diffusion coefficient and proposed extending this simulation to moisture contents above the FSP.
In numerical terms, the finite volume method (Patankar, 1980) was implemented in order to integrate the diffusive transport equation, using a central difference for the second order derivatives and an implicit Euler scheme for the transitory term.
The parameters that ultimately determined the relationship between moisture content and moisture flow were calculated by solving the following inverse problem: Given a known drying curve and known moisture distributions in certain sections, we determined the effective diffusion coefficient in order to simulate the drying process using a diffusive transport equation. Moreover, it was necessary to calculate the mass convection coefficient required as a boundary condition at the wood/drying environment interface.
The objective of this work was to simulate the one-dimensional drying process of radiata pine over the entire moisture range using the concept of effective diffusion coefficient, which is dependent on the moisture content as proposed by Comstock (1963). This was used for one-dimensional modeling in the radial and tangential directions of a transversal plane of radiata pine. Our experiments provided transitory distributions of moisture gradients and drying curves, which were then used to determine the radial and tangential effective diffusion coefficients and to validate the proposed modeling.
II. MATERIALS AND METHODS
A. Description of experiments
Radiata pine wood was dried in a climate-controlled chamber for convective drying at a low temperature, with an average air flow velocity of 1.6 (m/s) and dry and wet bulb temperatures of 44 and 36 (°C), respectively. The experimental design contemplated the use of seven samples of wood (P1 to P7) for each direction of study (radial and tangential). The wood samples measured 40x40x40 (mm), and their faces were oriented in the typical orthotropic directions of wood (radial, tangential, longitudinal). The samples were selected of a twenty-year old radiate pine tree growing in the Bio-Bio region in the south of Chile according to Chilean norms for testing and procedure to determine moisture content (INN, 1984; INN, 1986). A one of the sample's faces were covered with silicone and aluminum foil; the uncovered face was oriented normal to moisture flow of interest and parallel to air flow direction (See Fig. 1a).
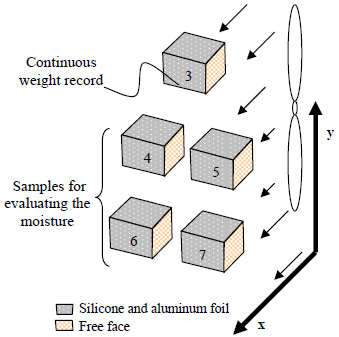
a)

b)
Figure 1. Experiment set E2: a) placement of samples, b) view of the installation inside the climate chamber.
Two experiments (E1 and E2) were performed for each direction of study (see Fig. 1). In the first experiment (E1), two wood samples (P1, P2) were subjected to the drying process. Sample P1 was connected to a balance (A&D model DF4000 with accuracy 0.1 g and measure error ± 0.1 g) that continuously measured its variation in weight. Later, the dry mass (anhydrous) of sample P1 was determined by drying for 24 hours in a Memmert oven conditioned with dry air at 103 (°C). The dry mass was used to calculate the water mass (M) according to Eq. (1).
These data allowed us to obtain an experimental drying curve and to select the drying times at which spatial moisture distributions would be determined. Sample P2 was used to monitor the temperatures inside the sample by using T-type thermocouples. The data were collected in a data acquisition system (Fluke, Hydra II model, accuracy ± 0.5 °C). Both devices (balance and Hydra II) were connected to a computer to store the respective data.
 | (1) |
where CH is the moisture content (%), mm is the moist mass (kg), md the anhydrous mass (kg), and M the water mass (kg).
The second experiment (E2, see diagram in Fig. 1) involved the remaining five samples (P3 to P7) and employed the same drying conditions as E1. Sample P3 was used to measure the average water mass, which was monitored continuously on a balance. Samples P4 to P7 were used to take transitory samples of the spatial distribution of the moisture content throughout the drying process at the times set with data obtained in E1. For it, each sample was sectioned into five normal slices considering the moisture flow direction of interest, and the wet weights of each were determined. Later, as in E1, we determined |the anhydrous mass for sample P3 and for each one of the sections obtained from samples P4 to P7 using a Boeco precision balance model BPB32; 0.01 g (See Fig. 2). These values were used to determine the water content according to Chilean norm INN (1984).

Figure 2. Boeco balance (model BPB32, Accuracy 1 mg with measure error ± 0.05 %) used to determine the mass of each section of samples P4 to P7.
B. Effective Diffusion Coefficient
The effective diffusion coefficient (D) was obtained with an exponential-type function suggested by Hukka (1999). When applied to the case of isothermal drying, this coefficient can be described by the following expression:
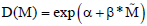 | (2) | |
| Where |  | |
| FSP = 0.603 - 0.001*Td (Simpson and Liu, 1997) | ||
| Td temperature of dry bulb (K) |
Thus, parameters α and b were determined for each direction of study, as was the mass convection coefficient S (m/s). This was done by solving the following inverse problem: Given a known spatial moisture distribution at certain characteristic points along the drying curve, we calculated the aforementioned parameters (α, b, S) such that the experimentally determined moisture distributions could be simulated.
For this, we carried out an extensive search for these parameters. We chose those that presented a minimum difference between the experimental and simulated data (see Fig. 3). This difference was determined from the following error function:
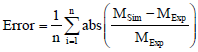 | (3) |
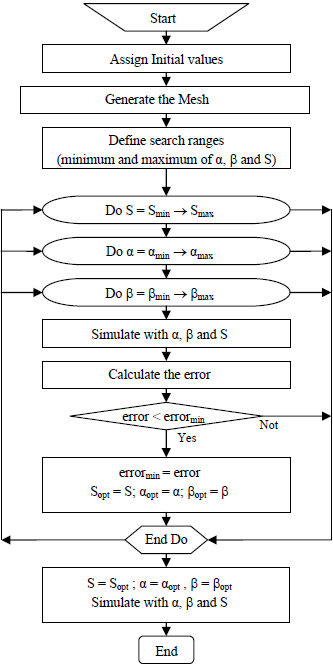
Figure 3. Flow chart of the algorithm used to determine the optimum values of parameters α, b, and S.
III. MATHEMATICAL/NUMERICAL MODEL
The mathematical model consisted of a partial, differential, non-linear equation of the second order that described the phenomenon of one-dimensional transitory diffusion (direction x) of the water mass M (kgw):
 | (4) |
where D is the effective diffusion coefficient (m2/s), in particular, the function of the water mass M.
The initial and boundary conditions were the following:
| M = M0 for t = 0 | (inicial) | |
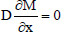 | in x = 0 | (symmetry) |
 | in x = L | (convection) |
The numerical integration of this differential model was done with the finite volume method. For this, the domain 0 < x < L was subdivided into N subdomains (finite volumes) (∀i (i=1,N)), the centroid of which contained the average value of the variable distinguished by the subscript p (MP) and the values of M in the adjacent volumes: behind (MW) and forward (ME). The limits of finite volumes (FV) centered on P were identified by w and e, respectively (see Fig. 4).

Figure 4. Discretization scheme of variables.
Integrating (4) according to FV shown in Fig. 4, we have:
 | (5) |
According to the rule of the middle point, the integrals of the transient terms and considering the fundamental theorem of calculus, we have:
 | (6) |
Now, evaluating the derivatives of M in the central form and the temporal derivative according to Euler fully implicit scheme:
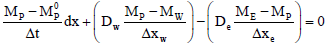 | (7) |
where M0 is the value of M in the previous time.
By grouping terms, we can write the generic algebraic equation for an FV centered on the P node as:
| awMW + (ap + at) Mp + aeME = bp | (8) | ||
| Where | 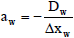 | ||
 | |||
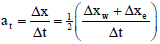 | |||
| ap = -(aw + ae) + at | |||
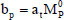 | |||
Thus, we were able to write n-2 equations of the type (one for each internal volume). Two are discounted since the volumes of their ends were special (not generic), requiring the incorporation of the boundary conditions.
For the initial FV subject to a boundary condition of no flow (in our case, this represents symmetry), we have:
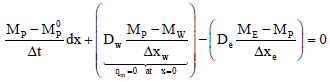 | (9) |
Thus, grouping terms according to Eq. (8), we have: aw with ae, at, bp, and ap as defined in the generic equation. That is, by evaluating the coefficientaw, we gave form to the special equation of the FV with a contour coinciding with the initial end, where we applied a boundary condition of symmetry.
Likewise, for the final FV subjected to a boundary condition of convection (in this case, representing the end exposed to the drying environment), we get:
 | (10) |
At this point, the value of the variable at end e (Me) is necessary. This can be obtained by linearly extrapolating based on the values of M in P and W; that is:
 | (11) |
Thus, by grouping terms to take them to the form of Eq. (8), we get:
| ae = 0 |
 |
| ap = -aw + S + at |
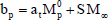 |
| at as defined in the generic equation |
For greater clarity, according to that described in Fig 4, Eq. (8), (9) and (10) make up the following equations system.
 | (12) |
As can be seen, a tridiagonal system of equations is obtained for each calculation. Thus, the TDMA algorithm known as the Thomas algorithm can be used to efficiently solve these systems (Lapidus and Pinder, 1982), thereby providing the spatial moisture distribution.
IV. RESULTS
The results obtained from our experiments show that the behavior of radiata pine wood is classic in terms of differentiating three drying ranges. The first range is from green wood to the critical moisture content (CMC; estimated to be 65% in the present study). This range is characterized by a predominant free flow of water with the front of evaporation at the wood/drying environment interface and moisture distributions with low variability (rather flat moisture distribution profiles).
The second drying range involves moisture contents from the CMC to the FSP and is characterized by the shift of the evaporation source towards the interior of the wood. These results in lower drying rates and a marked slope of the moisture distribution towards the wood/drying environment interface (markedly parabolic moisture distribution profiles).
Finally, near the fiber saturation point (FSP), the drying rates drop noticeably due to the additional requirements of disconnecting and transporting the water from the cell walls. In this range, the diffusive transport phenomenon is dominant and the spatial moisture distributions maintain their parabolic shape (note that the physical parameter FSP is considered in the effective diffusion coefficient function). Given the previous observation, we chose to simulate the drying process, distinguishing specific functions for effective diffusion above and below the CMC, which is fundamental for an effective simulation of drying from the green state.
Table 1 contains the values of parameters α, b and S determined for the radial and tangential directions, distinguishing drying ranges above and below the CMC.
Table 1. Parameters α, b and S.
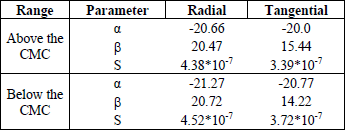
The values of the coefficient S fall within the range of magnitude reported by literature (Siau, 1995; Pang, 1996).
As the moisture content of the wood declines, the effective diffusion coefficient diminishes noticeably. For moisture content about FSP, the effective diffusion coefficient values are similar ones given for other authors at comparable temperatures (see Fig. 5).

Figure 5. Effective Diffusion Coefficients below FSP.
Figures 6 to 9 show experimental and numerical results of drying curves and spatial moisture distributions. In particular, Fig. 6 and 8 show the one-dimensional drying curves in the tangential and radial directions. Therein, we can see the orderly dispersal of the experimental data obtained by the continuous monitoring of the weight of sample 3 during drying. We used the average of these values, which are very close to those simulated by the proposed model (less than 2% difference), to define an experimental drying curve. Moreover, these figures highlight the drying states in which the spatial moisture distributions were evaluated.

Figure 6. Drying curves for the tangential direction.

Figure 7. Moisture content for the tangential direction.

Figure 8. Drying curves for the radial direction.

Figure 9. Moisture content for the radial direction.
Figures 7 and 9 show the spatial moisture distributions in the tangential and radial directions, respectively, evaluated every 24 (h) of drying. As mentioned earlier, we observed a noteworthy change in the curvature of the moisture distribution profiles related to the moisture content. The observation of the profiles allows us to infer that the moisture distribution profiles have a low curvature and/or are rather flat when the moisture contents exceed the CMC (around 65%), whereas moisture contents below this threshold are markedly parabolic. The effective simulation of this phenomenon was done by differentiating the function that determined the effective diffusion coefficients above and below the CMC. This led to high magnitude effective diffusion coefficients above the FSP. As can be seen in these figures, the approximation of the simulations to the experimental data is adequate: Average error less than 1% with maximum about 5%.
V. CONCLUSION
We can conclude that the model presented allows a satisfactory simulation (simple, with a good approximation and low computational cost) of the conventional isothermal drying process of radiata pine wood based on the effective diffusion coefficient for overall drying process.
The ability to distinguish the function that determines the effective diffusion coefficients above and below the CMC is fundamental for an effective simulation in terms of the drying process from the green state.
The optimization strategy of the function that determines the effective diffusion coefficients through an extensive searching scheme, which implies solving an inverse problem, is effective for determining the parameters of said function and the coefficient of mass convection required at the wood/drying environment interface.
Simulations above the FSP are conditioned by high effective diffusion coefficients, which drop noticeably with lower wood moisture contents.
The present methodology could be extended to two and three dimensions with no more difficulty than that caused by the multiple data and the computational cost.
VI. NOMENCLATURE
| P | Samples |
| E | Experiment |
| CH | Moisture content (%) |
| M | Water mass (kg). |
| D | Effective diffusion coefficient (m2/s) |
| α, β | Effective diffusion constants |
| FSP | Fiber Saturacion Point |
| T | Temperature (K) |
| Error | Average error |
| t | Time (s) |
| x | Spatial co-ordinate (m) |
| L | Total length (m) |
| ∀ | Finite volume |
| CMC | Critical Moisture Content (%) |
| S | Convection coefficient (m/s) |
| a | Matrix coefficient |
| b | Vector coefficient |
| m | mass (kg) |
Subscripts
| m | moist |
| d | dry |
| Sim | Simulated |
| Exp | Experimental |
| P | Finite volume center |
| W | Adjacent West finite volume center |
| E | Adjacent East finite volume center |
| w | Adjacent West boundary |
| e | Adjacent East boundary |
| i | knot |
| s | Surface |
| ∞ | Environment |
| min | Minimum |
| max | Maximum |
| opt | Optimum |
REFERENCES
1. Ananías, R.A., S. Vallejos and C. Salinas, "Estudio de la cinética del secado convencional y bajo vacío del pino radiata," Maderas. Ciencia y tecnología, 7, 37-47 (2005). [ Links ]
2. Chen, X.D., "Moisture diffusivity in food and biological materials," Drying Technology, 25, 1203-1213 (2007) [ Links ]
3. Comstock, G.L., "Moisture diffusion coefficients in wood as calculated from adsorption, desorption and steady state data," Forest Products Journal, 13, 97-103 (1963). [ Links ]
4. Davis, C.P., C.G. Carrington and Z.F. Sum, "The influence of compression wood on the drying curves of pinus radiata dried in dehumidifier conditions," Drying Technology, 20, 2005-2026 (2002). [ Links ]
5. Hukka, A., "The effective diffusion coefficient and mass transfer coefficient of nordic softwoods as calculated from direct drying experiments," Holzforschung, 53, 534-540 (1999). [ Links ]
6. Keey, R., T. Langrish and J. Walker, Kiln drying lumber, Springer, N. York (2000). [ Links ]
7. Lapidus, L. and G.F. Pinder, Numerical solution of partial differential equations in science and engineering. John Wiley & Sons Inc. (1982). [ Links ]
8. Luikov, S.A.V., Heat and mass transfer in capillary porous bodies. Pergamon Press, Oxford. pp 522 (1966). [ Links ]
9. INN, Madera. Parte 1: determinación de humedad, Instituto Nacional de Normalización, Santiago, Chile, NCH 176/1 Of84 (1984). [ Links ]
10. INN, Madera. Selección, obtención y acondicionamiento de muestras y probetas para la determinación de propiedades físicas y mecánicas, Instituto Nacional de Normalización, Santiago, Chile, NCh 968. Of. 1986 (1986). [ Links ]
11. Pang, S., "External heat and mass transfer coefficients for kiln drying of timber," Drying Technology, 14, 859-871 (1996). [ Links ]
12. Pang, S., "Relationship between a diffusion model and a transport model for softwood drying," Wood and Fiber Science, 29, 58-67 (1997). [ Links ]
13. Patankar, S.V., Numerical heat transfer and fluid flow, Hemisphere Publishing Corporation, Washington DC (1980). [ Links ]
14. Rozas, C., I. Tomaselli and E. Zanoelo, "Internal mass transfer coefficient during drying of softwood (Pinus elliotti) boards," Wood Science and Technology, 43, 361-373 (2009). [ Links ]
15. Salinas, C., R.A. Ananías and P. Ruminot, "Modelación Fenomenológica del Secado de Madera de Pino Radiata a Alta Temperatura," Maderas. Ciencia y tecnología, 10, 207-217 (2008). [ Links ]
16. Siau, J.F., Transport Processes in Wood. Springer, New York (1984). [ Links ]
17. Siau, J.F., Wood: Influence of moisture on physical properties, VPI and State University, USA (1995). [ Links ]
18. Simpson, W.T. and J.Y. Liu, "An optimization technique to determine red oak surface and internal moisture transfer coefficients during drying," Wood and Fiber Science, 29, 312-318 (1997). [ Links ]
19. Smith, S. and T. Langrish, "Multicomponent solid modeling of continuos and intermittent drying of Pinus radiata sapwood below the fiber saturation point," Drying Technology, 26, 844-854 (2008). [ Links ]
20. Stamm, A., Wood and cellullose science, Ch. 23: Diffusion in wood. Ronald Press, New York (1964). [ Links ]
21. Whittaker, S., "Simultaneous heat, mass, and momentum transfer in porous media: A theory of drying," Advances in Heat Transfer, 13, 119- 203 (1977). [ Links ]
Received: January 27, 2010.
Accepted: June 22, 2010.
Recommended by Subject Editor Walter Ambrosini.














