Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Latin American applied research
Print version ISSN 0327-0793
Lat. Am. appl. res. vol.41 no.2 Bahía Blanca Apr. 2011
ARTICLES
Finite volume simulation of 2-D and 3-D non-stationary magnetogasdynamic flow
M. Martínez, S. Elaskar, L. Maglione* and A. Scarabino
Grupo Fluidodinámica Computacional, Universidad Nacional de La Plata, La Plata, 1900, Argentina.
mmartinezk@ing.unlp.edu.ar, scarabino@ing.unlp.edu.ar
Universidad Nacional de Cordoba and CONICET, Córdoba, 5000, Argentina. selaskar@yahoo.com
* Facultad de Ingeniería, Universidad Nacional de Río Cuarto. smaglione@ing.unrc.edu.ar
Abstract - This work presents the development of the ideal and real magnetogasdynamic (MGD) equations in two and three spatial dimensions, followed by a modern numerical resolution method. The equations that govern the MGD flows are continuity, momentum, energy and magnetic induction together with a state equation. The method of Roe has been applied, in a high resolution Total Variation Diminishing scheme, with modifications proposed by Yee et al. For the implementation of this method in finite volumes a FORTRAN code has been developed, and it has been applied to the resolution of the magnetogasdynamic Riemann problem and the Hartman flow. Due to the high computational cost demanded by a 3D simulation, it has been necessary to reduce the grid density, compared to that used on the unidimensional and bidimensional cases. In order to evaluate this last issue, an analysis of the effect of the grid density on the results has been included at the end of the present work. The magnetogasdynamic shock tube and the Hartman flow, used as "benchmarks", have been satisfactorily solved.
Keywords - Magnetogasdynamics; Riemann Problem; Hartman Flow; TVD Scheme.
I. INTRODUCTION
The magnetogasdynamics is the branch of physics that studies the flow of compressible ionized fluids. The governing equations are those of continuity, Newton's second law, conservation of energy, Maxwell's equations and equations of state for the involved fluids. This set of equations must be completed, with thermo-chemical models for fluids at very high temperatures (D'Ambrosio and Giordano, 2004). The magnetogasdynamic analysis can be classified in three categories, depending on the hypothesis assumed for the flow and the governing equations:
-Ideal Magnetogasdynamics (IMGD): the system is described by Euler equations plus the magnetic induction equation.
-Real Magnetogasdynamics (RMGD): the system is described by Navier-Stokes equations plus the magnetic induction equation
-Complete Magnetogasdynamics (CMGD): the system is defined by the coupled Navier-Stokes and Maxwell equations.
In all cases it is possible to have more than one specie and chemical reaction between them, which are modeled as source terms. It is also necessary to specify equations of state.
The main objective of this work is to present the results obtained with a computational code developed to solve the non-stationary 3-D ideal and 2-D real magnetogasdynamic equations using an approximated Riemann solver and with a Total Variation Diminishing (TVD) scheme. This research intends to contribute to achieving a comprehensive description of the ablative pulse plasma thruster (APPT) behavior. There is previous work (Elaskar and Brito, 2001) in which the authors use numerical codes to simulate the flow inside of magnetoplasmadynamics thruster.
The new 3-D code presented in this work is a natural extension of the 2-D code developed by Maglione (2004) and the works of Maglione et al. (2003, 2007).
An application of particular interest of IMGD is the propagation of waves in solar magnetic loops (Fernandez et al., 2009) and the evolution of solar tadpoles (Costa et al., 2009).
Among other researchers work in this line, Keppens (2001) uses Roe's approximation to a Riemann solver, Sankaran (2003) develops a "Local Extremum Diminishing-LED" scheme, D'Ambrosio et al. (2004) solve the time-dependent complete magnetogasdynamics equations (CMGD) in one spatial dimension and Loverich (2004) simulates the Magnetohydrodynamic (MHD) equations considering two substances, with Roe's approximation.
This work offers a comparison between the results obtained with our 3-D ideal MGD code and those obtained with the previous 2-D code, in order to validate the first one. During the tests of our software, which were performed using a lower density mesh, due to our limited computing facilities, slight differences were noticed between the results and those obtained with a higher density mesh in 2-D. For that reason it was decided to extend the scope of this work, by carrying out a comparison between the results obtained with meshes of different density. In this way it was possible to establish the effect that the mesh density introduces in the results in this sort of problems and to confirm that the differences between the 3-D results and those from 2-D computations corresponded to mesh density effects. Together, results obtained by two dimensional real MGD simulations for the Hartmann flow are presented and compared with analytical solutions. It is important to note that this last benchmark corresponds to steady flow and incompressible plasma.
II. MGD EQUATIONS
The real magnetogasdynamics equations (RMGD) characterize the flow of an ionized conducting fluid in the presence of magnetic fields. They represent the coupling of the viscous compressible fluid dynamics equations (Navier-Stokes equations) with Maxwell electrodynamics equations, considering only magnetic fields and neglecting electrostatic forces (Dendy, 1999),
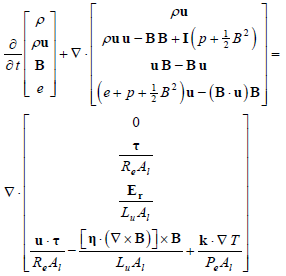 | (1) |
which we will write as
 | (2) |
where fh and fp represent the hyperbolic and parabolic flows respectively, and U is the vector of conserved variables
U = (ρ, ρux, ρuy, ρuz, Bx, By, Bz, e)T , (3)
with ∇ · Er = - ∇ × [η · (∇ × B) / µo]; ρ is the density, p the pressure, u the velocity vector and e the total energy. B is the magnetic field vector, µo the vacuum magnetic permeability,  the conductivity tensor and
the conductivity tensor and  the electric resistivity tensor. The viscous stress tensor is
the electric resistivity tensor. The viscous stress tensor is  , where µ is the non-dimensional viscosity and I is the unity tensor. The non-dimensional numbers are: Reynolds Re = ρref LU / µref; Alfvén Al = ca / U, Peclet Pe = LU / αref and Lundquist Lu = µoLU / ηref. The suffix "ref" indicates reference values, U and L are the characteristic velocity and the characteristic length, respectively. a is the thermal diffusivity coefficient and "ca" is the Alfvén velocity.
, where µ is the non-dimensional viscosity and I is the unity tensor. The non-dimensional numbers are: Reynolds Re = ρref LU / µref; Alfvén Al = ca / U, Peclet Pe = LU / αref and Lundquist Lu = µoLU / ηref. The suffix "ref" indicates reference values, U and L are the characteristic velocity and the characteristic length, respectively. a is the thermal diffusivity coefficient and "ca" is the Alfvén velocity.
If the diffusive effects are neglected, fp = 0, the ideal magnetogasdynamics equations are recovered. The system is hyperbolic, since its Jacobian matrix has real eigenvalues, and it is non linear. The resolution method, which will be developed in next sections, is for strictly hyperbolic systems; therefore some modifications must be introduced in the Jacobian matrix, in order to get eight different eigenvalues (Powell 1995).
Unlike non-conducting fluid mechanics, where only five waves appear in a 3-D formulation, MGD allows the existence of eight waves, their velocities given by the respective eigenvalues of the Jacobian matrix. The fastest wave, which is the fast magnetosonic wave, limits the time step in the numerical discretization.
In an orthonormal Cartesian coordinates system, the ideal magnetogasdynamics equations can be written in terms of "flows" for the three-dimensional case, as
 | (4) |
where F, G and H are "hyperbolic flow vectors" or "Godunov flows", because of the second version of Godunov's method, presented in 1976. For example,
 | (5) |
Vector fluxes G and H are of analogous formulation.
These flows will be computed in an analogous way as in the 1-D formulation of Elaskar et al. (2000) and the 2-D formulation of Maglione (2004).
III. NUMERICAL APPROXIMATION
An integral finite volume formulation is implemented in a structured spatial grid. The time derivatives are approximated with an upwind first-order explicit scheme. The hyperbolic numerical flows are evaluated using Roe's method (Roe, 1981), with the modifications introduced by Yee et al. (1985) and Yee (1989), employing the "Total Variation Diminishing - TVD" technique (Leveque, 2005). This methodology allows to have results of second order precision in the regions where the solution is smooth, and also to capture discontinuities without introducing spurious oscillations.
The problem studied is the flow in a magnetogasdynamics shock tube of length L, filled with an ionized gas that behaves in a way represented by Eqs. (1). In the middle section of the tube a discontinuity or diaphragm separates two different states of the gas. This ideal diaphragm is removed at the initial time of computation, starting the interaction between the two initial states of the gas. This process is modeled as a Riemann problem of Magnetogasdynamics in the following way: Eq. (4) is solved with initial condition
U(x, y, z, 0) = U0(x, y, z) (6)
and boundary conditions:
| U(0, y, z, t) = Ul(y, z, t) U(L, y, z, t) = Ur(y, z, t) U(x, H, z, t) = Ut(x, z, t) U(x, 0, z, t) = Ub(x, z, t) U(x, y, 0, t) = Uba(y, z, t) U(x, y, F, t) = Ufr(y, z, t) | (7) |
Subscripts l, r, t, b, ba and fr indicate respectively left, right, top, bottom, back and front boundaries.
The method originally suggested by Godunov (1959) consists basically in considering a constant value of conserved variables in each cell, and to solve a local Riemann problem in each cell boundary. Because local Riemann problems are lineal, they have an exact solution, given by a number of waves equal to the number of eigenvalues of the Jacobian matrix, with propagation velocities given by these eigenvalues. Between consecutive waves the conserved variables have constant values, as shown in Fig. 1. for a 1-D formulation.

Figure. 1 Exact solution to a 1-D Riemann problem. λi are eigenvalues corresponding to each wave.
In a later work, Godunov (1976) demonstrated that this problem could be solved by defining flows across cell boundaries, as expressed in Eq. (5). Later, other researchers proposed different ways of computing these flows, being Roe's method (Roe, 1981) one of the most extensively adopted. This method, with a TVD scheme, is the one chosen for this work.
IV. HIGH RESOLUTION METHOD.
A high resolution method is one with at least second order precision in smooth solutions, and able to detect and follow discontinuities without introducing numerical oscillations (Leveque, 2005). The general idea in this work is to use a high order method, modified with the objective of incrementing numerical dissipation near discontinuities, considering, for instance, the numerical flow as a combination of a high order flow FH and a low order flow FL.
One of the most common high resolution methods expresses the numerical flow as:
FH = FL + Φ (FH - FL) (8)
where Φ is a limiter function that changes smoothly the scheme between high and low resolution. In regions where the solution is smooth, Φ must be equal to 1, whereas in regions of high gradients, it must take values close to zero, in order to avoid numerical oscillations with no physical significance. Based on previous experience (Elaskar and Brito, 2001, Maglione et al., 2007), the minmod function (Roe, 1986) was chosen.
With the purpose of detecting accurately the expansion waves, Yee (1989) introduced in his scheme a function that modifies the eigenvalues absolute value as:
 | (9) |
The numerical flow proposed by Roe (1981) with the modifications introduced by Yee et al. (1985) is finally as follows:
 | (10) |
where
 | (11) |
Is the "minmod" limiter function with
 | (12) |
 | (13) |
Integer subscripts refer to cells and subscripts with ± ½ refer to cell boundaries. The numerical flow given by Eq. (10) is used to compute the temporal evolution of the conserved variables by means of Eq. (3). For the numerical computation, variables have been made non-dimensional, as in (Brio and Wu, 1988).
V. RESULTS
In this section are presented the results obtained for the 3-D shock tube problem and the Hartman flow.
A. Shock tube
A FORTRAN code was developed in order to implement the numerical computation of the flow with a AMD Athlon 64 X2 Dual Core 3800+ 2,1GHz processor with 1Gb RAM. A 200 x 70 x 70 element grid was close to the maximum that the compiler was able to process. Each 1500 time step run took more than 24 hs in this system. Results of runs in the 3-D geometry but with a 2-D flow were compared with those of a 2-D model obtained with a 1000 x 350 grid (Maglione, 2004), finding an almost complete concordance. At a second stage of the work different grid densities were tested in order to study the possible influence of this parameters in the results.
The comparisons between the results obtained using different mesh densities were made for similar 'time' instead of similar 'time step', since the time steps in this simulation are not constant in order optimize the computation, fulfilling the Courant-Friedrichs-Lewy condition:
 | (14) |
where, u= velocity , Δt= time step, Δx= mesh density and C = number defined for a specific problem. The condition must be fulfilled in all three dimensions.
For the magnetogasdynamics Riemann problem, the following initial values were considered at each side of the dividing diaphragm, expressed in primitive or physical variables, for comparison with previous results (Maglion, 2004; Maglione et al., 2003; Brio and Wu, 1988):
 | (15) |
From this initial state the following evolutions, shown in figures 2 to 8 were obtained for 1, 100, 200, 250, 300 y 500 time steps (t = 0.001, 0.014, 0.047, 0.095 and 0.289 respectively) at the duct central line, for the 200 x 70 x 70 grid.

Fig. 2 Density spatial distribution for different values of t (table) with 200x70x70 mesh.

Fig. 3 Pressure spatial distribution for different values of t (table) with 200x70x70 mesh.

Fig. 4 Longitudinal velocity distribution for different values of t (table) with 200x70x70 mesh.

Fig. 5 Vertical velocity distribution for different values of t (table) with 200x70x70 mesh.

Fig. 6 Lateral velocity distribution for different values of t (table) with 200x70x70 mesh.

Fig. 7 Vertical component of the magnetic field B for different values of t (table) with 200x70x70 mesh.

Fig. 8 Lateral component of the magnetic field B for different values of t (table) with 200x70x70 mesh.
In Fig. 2 one can observe five waves in the density field. From left to right, there are
- A fast expansion wave, traveling left
- A compound wave (the sharp peak) traveling left
- A contact discontinuity, traveling right
- A shock wave, traveling right
- A small fast expansion wave, traveling right.
In the Riemann problem for IMGD three of the eight original waves merge, reducing the number of waves to five (Udrea, 1999).
Figures 9 to 16 show some variables in the 3D computations using different grid densities: 200 x 70 x 70, 160 x 56 x 56, 100 x 35 x 35 and 40 x 14 x 14 respectively. The first two grids give practically the same results. The 160 x 56 x 56 grid detects correctly the position of the different waves, but produces naturally smoother gradients. The 40 x 14 x 14 grid is clearly of insufficient resolution for this problem.

Fig. 9 Density distribution for t = 0.2, in 2-D and 3-D simulations

Fig. 10 Pressure distribution for t = 0.2, in 2-D and 3-D simulations

Fig. 11. X Velocity components for t = 0.2, in 2-D and 3-D simulations.

Fig. 12. Y and Z velocity components 2D and 3D for t = 0.2.

Fig. 13. Magnetic Field 2D y 3D for t = 0.2.

Fig. 14. Density calculated with four different meshes for t=0.2.

Fig. 15.- Pressure calculated with four different meshes for t=0.2.

Fig. 16. X velocity component calculated with four different meshes for t = 0,2.
2. Hartman flow
The second benchmark is the Hartmann flow; it is an extension of Couette's flow for electrically conductive fluids (Sutton and Sherman, 1967). To solve this flow is necessary to incorporate the parabolic terms in the magnetogasdynamics equations.
In this problem the flow is steady-state, laminar and it develops between two, virtually infinite, parallel moving plates with opposite velocities of equal magnitude. The applied field is normal to the plates and constant. The Hartmann flow can be studied as a 2-D flow. The geometry is shown in Fig. 17.

Figure 17. Hartmann flow. Geometry.
Figures 18 and 19 show the comparison between the numerical and the analytical data for the Hartmann number Ha = 1 and 10 respectively (Maglione et al., 2007).

Figure 18. Hartmann flow. Ha = 1. Left velocity, right magnetic field. Theoretical solution: line. Numerical simulation: points.

Figure 19. Hartmann flow. Ha = 10. Left velocity, right magnetic field. Theoretical solution: line. Numerical simulation: points.
This benchmark corresponds to incompressible fluid and steady state flow. The code simulates correctly the Hartmann flow, even though it was developed to simulate compressible and time-dependent magnetogasdynamics flows.
VI. CONCLUSIONS
Numerical results have been presented in this work, obtained with a finite volume code, developed with the purpose of modeling the non-stationary three-dimensional flow of an ideal conducting fluid and non-steady two-dimensional real MGD equations. The code is based in a Roe solver modified by Yee et al, with a Total Variation Diminishing approximation technique.
Results obtained in the magnetogasdynamics shock tube have been satisfactory and in concordance with those of previous work, for one and two dimensional flows. This numerical methodology allowed to capture shock waves without oscillations, providing also good approximations in flow regions with no discontinuities.
The limitations in grid density imposed by the computational resources introduce some differences in the results, particularly smoother graphs, due to the lower resolution of this solution, compared with the one obtained for one and two-dimensional flows with denser grids. The analysis of the influence of grid density shows that the solution for 2-D problems computed with the 3-D code will converge for denser grids to the 2-D solution. It also highlights the limitations of coarse grids for this type of problems.
The developed 3-D code has been validated with the benchmark proposed by Brio and Wu (1988) in order to evaluate the behavior of codes for the numerical simulation of the magnetohydrodynamic equations.
To evaluate a steady-state problem the Hartmann flow was simulated, the results obtained in the Hartmann flow test have been successful. Some differences were founded between numerical and analytical solutions; however the software captures properly the nature of the solution. It is important to note that the code has been developed to solve time dependent and compressible magnetogasdynamics equations; the Hartmann flow is a benchmark that requires solving an incompressible and steady state flow.
Further works will include modeling dissipative effects in 3-D flow and test its in more complex geometries.
ACKNOWLEDGMENTS
This research work has been partially funded by the Argentine Council for Scientific and Technological Research, CONICET, through the grant PIP No 5692; it is also included in the project PICTO-UNRC-2005 No. 30339.
REFERENCES
1. Brio, M. and C.C. Wu, "An upwind differencing scheme for the equations of ideal magnetohydrodynamics", J. of Computational Physics 75, 400-422 (1988). [ Links ]
2. Costa, A., S. Elaskar, C. Fernández and G. Martinez, "Numerical simulation of dark inflow in post-flare-supra-arcade," Monthly Notices of the Royal Astronomical Society, 400, 85-89 (2009). [ Links ]
3. D'Ambrosio, D. and D. Giordano, "Electromagnetic Fluid Dynamics for Aerospace Applications. Part I: Classification and critical Review of Physical Models," AIAA Paper,2165 (2004). [ Links ]
4. D'Ambrosio, D., M. Pandolfi and D. Giordano, "Electromagnetic Fluid Dynamics for Aerospace Applications. Part II: Numerical Simulation Using Different Physical Models," AIAA Paper, 2362. (2004). [ Links ]
5. Dendy, R., Plasma Physics. An Introductory Course, Cambridge University Press, Cambridge (1999). [ Links ]
6. Elaskar, S. and H. Brito, "Solution of real magnetogasdynamics equations using a TVD scheme as a tool for electric propulsion," International Electric Propulsion Conference, Pasadena., IEPC-01-161 (2001) [ Links ]
7. Elaskar, S., C. Sanchez and H. Brito, "Numerical Tools for the Simulation of the APPT behaviour: Arc Generation and Plasma Flow," Third International Conference on Spacecraft Propulsion, Cannes, France, October (2000). [ Links ]
8. Fernández, C., A. Costa, S. Elaskar and W. Schulz, "Numerical simulation of the internal plasma dynamics of post-flare loops," Monthly Notices of the Royal Astronomical Society, 400, 1821-1828 (2009). [ Links ]
9. Godunov, S., "A Finite Difference Method for the Computation of Discontinuous Solutions of the Equations of Fluid Dynamics," Mat. Sb., 47, 357-393 (1959) [ Links ]
10. Godunov, S., Numerical Solution of Multi-Dimensional Problems in Gas Dynamics, Nauka Press, Moscow, (1976) [ Links ]
11. Keppens, R., "Dynamics controlled by magnetic fields: parallel astrophysical computations", Parallel Computational Fluid Dynamics - Trends and Applications, eds. C.B. Jenssen et al., Amsterdam, Elsevier Science B.V., 31-42 (2001). [ Links ]
12. Leveque, R., Numerical Methods for Hyperbolic Systems, Cambridge Text in Applied Mathematics, Cambridge (2005). [ Links ]
13. Loverich, J., A finite volume algorithm for the two fluid plasma system in one dimension, Master Thesis, University of Washington (2004). [ Links ]
14. Maglione, L. Simulación numérica del flujo magnetogasdinámico inestacionario en dos dimensiones, Master Thesis, Univ. Nacional de Río Cuarto, Argentina (2004). [ Links ]
15. Maglione, L., S. Elaskar and H. Brito, "Numerical simulation of two-dimensional, non-steady, ideal magnetogasdynamic equations," International Electric Propulsion Conference, Toulouse, IEPC-03-070. (2003). [ Links ]
16. Maglione, L., S. Elaskar, H. Brito, R. Dean and L. Lifschitz, "A software engineering for numerical simulation of 2D non-stationary real MGD flows," PAMM, 7, 2010027-2010029 (2007). [ Links ]
17. Powell, K., An approximate Riemann solver for magnetohydrodynamics (that works in more than one dimension), NASA Contract No NAS1-19489, ICASE, NASA Langley Research Laboratory, Hampton (1995). [ Links ]
18. Roe, P.L., "Approximate Riemann solvers, parameter vectors and difference scheme," Journal of Computational Physics, 43, 357-372 (1981). [ Links ]
19. Roe, P.L., "Characteristic-based schemes for the Euler equations," Ann. Rev. Fluid Mech., 18, 337-365 (1986). [ Links ]
20. Sankaran, K., Simulation of MPD Flows Using a Flux-Limited Numerical Method for the MHD Equations, Master Thesis, Princeton University (2003). [ Links ]
21. Sutton, G. and A. Sherman, Engineering Magnetohydrodynamics, MacGraw-Hill, New York (1965). [ Links ]
22. Udrea, B., An advanced implicit solver for MHD, PhD Thesis, University of Washington (1999). [ Links ]
23. Yee, H., R. Warming and A. Harten, "Implicit Total Variation Diminishing (TVD) Schemes for Steady-state Calculations," Journal of Computational Physics, 57, 327-360 (1985). [ Links ]
24. Yee, H., A class of high resolution explicit and implicit shock-capturing methods, NASA Report N89-25652 (1989). [ Links ]
Received: July 9, 2009.
Accepted: June 14, 2010.
Recommended by Subject Editor Alberto Cuitiño.














