Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. vol.41 no.4 Bahía Blanca oct. 2011
ARTICLES
Approximating the solution to lqr problems with bounded controls
V. Costanza and P.S. Rivadeneira
Nonlinear Systems Group, INTEC (UNL-CONICET). email: tsinoli@santafe-conicet.gov.ar
Abstract New equations involving the unknown final states and initial costates corresponding to families of LQR problems are shown to be useful in calculating optimal strategies when bounded control restrictions are present, and in approximating the solution to fixed-end problems. The missing boundary values of the Hamiltonian equations are obtained by (offline) solving two uncoupled, first-order, linear partial differential equations for two auxiliary n × n matrices, whose independent variables are the time-horizon duration T and the eigenvalues of the final-penalty matrix S. The solutions to these PDEs give information on the behavior of the whole (T, S)-family of control problems. Illustrations of numerical results are provided and checked against analytical solutions of the cheapest stop of a train' problem.
Keywords Optimal control; Constrained control; Linear-quadratic problem; First order PDEs; Boundary-value problems; Riccati equations.
I. INTRODUCTION
The linear-quadratic regulator (LQR) is probably the most studied and quoted problem in the state-space optimal control literature. The main line of work in this direction has evolved around the algebraic (ARE, for infinite-horizon problems) and differential (DRE, for finite-horizon ones) Riccati equations. When expressed in 2n-phase space, i.e. introducing the costate (in the smooth case, the gradient of the value function), the dynamics of the optimal control problem takes the form of Hamilton's classical equations of fundamental Physics.
Since the early sixties, Hamiltonian formalism has also been at the core of the development of modern optimal control theory (see Pontryagin et al., 1962). When the problem concerning an n-dimensional system and an additive cost objective is regular (Kalman et al., 1969), i.e. when the Hamiltonian of the problem can be uniquely optimized by a control value udepending on the remaining variables (t, x, ?), then a set of 2n ordinary differential equations (ODEs) with twopoint boundary-value conditions, known as Hamilton's (or Hamiltonian) Canonical Equations (HCEs), has to be solved. This is often a rather difficult numerical problem for nonlinear systems. For the linearquadratic regulator (LQR) with a finite horizon, there exist well known methods (see for instance Bernhard, 1972; and Sontag, 1998) to transform the boundaryvalue problem into an initial-value one. In the infinitehorizon, bilinear-quadratic regulator and change of set-point servo, there also exists an attempt to find the missing initial condition for the costate variable, which allows to integrate the equations on-line with the underlying control process (Costanza and Neuman, 2006).
Usual Hamiltonian systems are those modelled by a 2n-dimensional ODE whose vector field can be expressed in terms of the partial derivatives of an underlying 'total energy' function -called 'the Hamiltonian'which is constant along trajectories. The ODEs for the state and costate of an optimal control problem constitute a Hamiltonian system from this general point of view. Richard Bellman has contributed in many fields, but he was particularly interested in symplectic systems coming from Physics (see for instance Abraham and Marsden, 1978) when he devised a partial differential equation (PDE) for the final value of the state x(tf) = ?(T,c) as a function of the duration of the process T = tf - t0, and of the final value imposed on the costate ?(tf) = c (one of the boundary conditions, the other being the fixed initial value of the state x(t0) = x0, see Bellman and Kalaba, 1963). Bellman exploited in that case ideas common to the 'invariant imbedding' numerical techniques, also associated with his name.
In Costanza (2008a) the invariant imbedding approach was generalized and new PDEs were found for the one-dimensional nonlinear-quadratic finite-horizon optimal control situation, where the final value of the costate depends on the final value of the state, i.e. c = c(?). The procedure followed in this proof induces a quasilinear PDE for the initial value s of the costate ?(t0), which was actually the main concern from the optimal control point of view. The firstorder equation for s can be integrated after the PDE for the final state ? (independent of s) has been solved. The 'initial' condition for s depends on the final value of the state and on the weight matrix S involved in the quadratic final penalty x'(T)Sx(T). Therefore it seems more natural to choose here (T,S) as the independent parameters of the family of control problems under consideration. Provided the solution s(T,S) is obtained, then the HCE can be integrated on-line for each particular pair of parameter values, and the optimal control can be constructed at each time the HCE solution becomes available.
The solutions ?(T,S),s(T,S) are also useful to generate a compensation component for the control, needed when the state solution to the HCE differs from the actual state of the system, due to perturbations. This allows to device a whole 'two-degrees-of-freedom' scheme for nonlinear optimal regular problems (see Costanza, 2009; for more details).
In this paper the application of these solutions to treat fixed-end and bounded-control problems in the linear quadratic context is explored and some promising results are shown. The main contributions are: (i) the formulation of new first order linear PDEs for the LQR problem in the n-dimensional case for a general nonnegative semidefinite final penalty matrix S, and (ii) the proposal of a technique to approximate the solutions to LQR problems with fixed final states under unbounded or bounded controls.
After some notation and general characteristics of the problem are exposed in section II, then the main PDEs for auxiliary matrices leading to the missing boundary conditions accepting a general nonnegative matrix S are proved in section III. The fixed-endpoint and bounded-control problems, with numerical validations and illustrations are discussed in section IV, in the context of a classical two-dimensional problem. There it is shown that the optimal control obtained through the analytical treatment of the case-study can also be calculated from the main objects substantiated in this paper, namely, the solutions to the matrix PDEs introduced in Section III. The whole approach is summarized in the final section V.
II. FORMULATION OF THE LQR PROBLEM FOR FREE FINAL STATES AND UNCONSTRAINED CONTROLS.
The classical finite-horizon, time-constant formulation of the 'LQR problem' for finite-dimensional systems with free final states and unconstrained controls, attempts to minimize the (quadratic) cost
 | (1) |
with respect to all admissible (let us assume piecewisecontinuous) control trajectories u : [0,T] ?  of duration T applied to some fixed, deterministic (linear) plant; i.e. those controls affecting the
of duration T applied to some fixed, deterministic (linear) plant; i.e. those controls affecting the  -valued states x of the system through the initialized dynamic constraint
-valued states x of the system through the initialized dynamic constraint
 | (2) |
The (real, time-constant) matrices in Eqs. (1, 2) normally have the following properties: Q, S are  , symmetric and positive-semidefinite, R is
, symmetric and positive-semidefinite, R is  and positive-definite, A is
and positive-definite, A is  , B is
, B is  , and the pair (A, B) is controllable. The expression under the integral is usually known as the 'Lagrangian' L of the cost, i.e.
, and the pair (A, B) is controllable. The expression under the integral is usually known as the 'Lagrangian' L of the cost, i.e.
 | (3) |
Under these conditions the Hamiltonian of the problem, namely the  function defined by
function defined by
 | (4) |
is known to be regular, i.e. that H is uniquely minimized with respect to u, and this happens for the explicit control value
 | (5) |
(in this case, independent of x), which is usually called 'the H-minimal control'. The 'Hamiltonian' form of the problem (see for instance Sontag, 1998) requires then to solve the two-point boundary-value problem
 | (6) |
 | (7) |
where H0(x, ?) stands for H(x, ?, u0(x, ?)), and  for the column vectors with i-components
for the column vectors with i-components  , respectively, i.e. Eqs.(6,7) here take the form
, respectively, i.e. Eqs.(6,7) here take the form
 | (8) |
with  . In the following section a novel approach to the solution (known to exist and be unique in this case), based on imbedding the individual situation into a two-parameter family of similar problems, will be presented and substantiated.
. In the following section a novel approach to the solution (known to exist and be unique in this case), based on imbedding the individual situation into a two-parameter family of similar problems, will be presented and substantiated.
III. EQUATIONS FOR THE MISSING BOUNDARY VALUES x(T) AND ?(0).
It is well known that the LQR problem as posed above can be solved via the Riccati differential equation (DRE)
 | (9) |
leading to the optimal feedback
 | (10) |
where P(t) is the (unique) positive-definite solution to equation (9). An alternative classical approach (see for instance Bernhard, 1972) transforms the original boundary-value problem into an initial-value one, by introducing the following auxiliary objects:
(i) the Hamiltonian matrix H,
 | (11) |
(ii) the augmented Hamiltonian system (a linear 2ndimensional matrix ODE with a final condition) defined for the combination of two  matrices X(t), ?(t), t ? [0, T] through
matrices X(t), ?(t), t ? [0, T] through
 | (12) |
The solution to the augmented (linear) problem (12) being unique, must verify
 | (13) |
and since in this case Eq. (8) also reads
 | (14) |
then the missing boundary conditions can be explicitly found, namely
 | (15) |
 | (16) |
 | (17) |
 | (18) |
(see Sontag, 1998; for a proof of the invertibility of X and other details). Actually, the whole solution to the DRE can be recovered from the solution to problem (12), explicitly
 | (19) |
As will become clear in the following sections, it is desirable to count with the missing boundary values for different values of the parameters (T, S) without solving either the DRE or the augmented system described above. A novel approach (in what follows called the 'PDE method') to solve the whole (T, S)family of LQR problems (with common A, B, Q, R, x0 values) is described below. The method starts by defining, for each particular (T, S)-problem,
 | (20) |
 | (21) |
 | (22) |
where the superscript  refers to the individual problem of duration T and final penalty matrix S. Then Eq. (13) can be rewritten in the form
refers to the individual problem of duration T and final penalty matrix S. Then Eq. (13) can be rewritten in the form
 | (23) |
Since the subjacent Hamiltonian system is linear, its solutions depend smoothly on parameters and initial conditions, and then the (partial) derivative of Eq. (23) with respect to T (denoted by the subscript 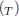 ) results
) results
 | (24) |
where the variables (T, S) have been dropped for clarity here and whenever convenient and clear through the rest of the paper. At this point, it is convenient to start by adopting the simplest expressions for matrix S, to make sense of the partial derivatives  with respect to the second parameter.
with respect to the second parameter.
A. The scalar (S = sI) case
In this subsection the form of the final penalty matrix will be scalar, i.e. S = sI, s ?  . The partial derivatives of Eq. (23) with respect to the real variable
. The partial derivatives of Eq. (23) with respect to the real variable
 | (25) |
Now, by partitioning U into  submatrices Ui, i = 1,... 4 in the form
submatrices Ui, i = 1,... 4 in the form
 | (26) |
then Eq. (25) reads
 | (27) |
which combined with Eq. (23) gives
 | (28) |
By inserting these results in Eq. (24), the following relations are obtained
 | (29) |
 | (30) |
where
 | (31) |
 | (32) |
These are first-order quasilinear PDEs for the matrices a, ß. Boundary conditions for a process of zero horizon are imposed in view of Eqs. (22, 17, 18), i.e.
 | (33) |
If the solutions a, ß for this problem are found, then the desired missing values for the state and costate, for any (T, s)-problem may be recovered immediately, namely
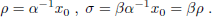 | (34) |
Illustrations of the behavior of solutions to these PDEs can be found for instance in Costanza (2008a) and Costanza and Neuman (2009).
B. Extension to a general S
Although in Section IV only scalar S matrices will be used, the general case of a positive semi-definite symmetric final penalty matrix S is discussed below. First, for the diagonal case, i.e. for S = diag(s1, s2,..., sn), where si = 0, i =1,..., n, the following identity can be easily obtained after differentiating the first equality in (23):
 | (35) |
where  = diag(0,..., 0, 1, 0,..., 0), with the "1" in the ith position (the sub-index n refers to the dimension of the state space). Then, by defining
= diag(0,..., 0, 1, 0,..., 0), with the "1" in the ith position (the sub-index n refers to the dimension of the state space). Then, by defining
 | (36) |
the condensed expression of Eq. (35) follows
 | (37) |
As a consequence, Eqs. (27) need only a slight modification in this context (S instead of s), i.e.:
 | (38) |
which combined with Eq. (23) gives
 | (39) |
and it is immediate to confirm that Eqs. (29-32) retain their form, i.e.
 | (40) |
Therefore, for a diagonal S the PDEs remain linear but they should be integrated in the (n + 1) independent variables (T, s1,..., sn). Finally, for a general (symmetric, positive-semidefinite) matrix S, it is well known that S can be diagonalized via an orthogonal matrix E (which depends on S), i.e.
 |
Then, after defining
 | (41) |
and maintaining the original definition (23) for a and ß, and by using definitions (36) and Eq. (37), then the following relations can be easily derived:
 | (42) |
 | (43) |
 | (44) |
 | (45) |
C. Relations amongst PDEs' solutions, Riccati equations, and feedback control.
For any (T, S)-LQR problem the optimal initial costate has the form
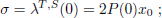 | (46) |
where P (·) is the numerical solution of the corresponding DRE, i.e. the final-value matrix ODE in Eq. (9). Therefore, from Eqs. (34, 46), for each (T, S)-problem the Riccati matrix P (·) should also verify
 | (47) |
allowing to solve the DRE as an initial-value problem (eventually on-line with the dynamics). But actually, as shown below (see Eq. 51) the PDE method for missing boundary conditions avoids solving the DRE for each particular (T, S)-problem. It also avoids storing, necessarily as an approximation, the Riccati matrix P(t) for the values of t ? [0, T] chosen by the numerical integrator, possibly different from the time instants for which the control u(t) is constructed. Instead, the HCEs (6, 7) can be integrated with initial conditions
 | (48) |
rendering the optimal trajectories x*(t), ?*(t) for 0 = t = T, which allow to generate the optimal control at each sampling time
 | (49) |
Even better, the feedback form for the control becomes directly available due to the linear dependence of Eqs. (34) on initial conditions, namely
 | (50) |
since ?*(t) is also the optimal initial costate for the problem with parameters (T - t, S) starting at x(0) = x*(t). Then, as a side-product, an alternative formula for the Riccati matrix results:
 | (51) |
More complex PDEs have been derived and applied, for the one-dimensional nonlinear case, in Costanza (2008a) and Costanza and Rivadeneira (2008); and for the n-dimensional nonlinear case, in Costanza (2008b) and Costanza et al. (2011).
IV. FIXED-ENDPOINT AND BOUNDED-CONTROL PROBLEMS
Optimal control problems with hard restrictions on final state values, or with other constraints on states or control values, require for their solution some version of the Pontryagin Maximum Principle (PMP). The objective of this Section is to show that, notwithstanding the generality of PMP, the solution to the PDEs described above may be also helpful in: (i) approximating the PMP solution of some fixed-end problems, (ii) approximating some fixed-end problems whose PMP solutions under constrained controls turn unfeasible in practice, and solving these approximate problems. These assertions will be substantiated through the treatment of a classical example (see for instance Agrachev and Sachkov, 2004; and for similar problems concerning the determination of optimal switching times, see Howlett et al., 2009, and their references therein).
A. The cheapest stop of a train
The case-study will have dynamics with the following simple linear form:
 | (52) |
or, in matrix notation,
 | (53) |
 | (54) |
where the real-valued control u may be interpreted as a braking action over an imaginary train with position x1 and velocity x2. The objective (in the original formulation) is to optimize the 'braking energy' needed to 'stop the train', i.e. to arrive at the exact final states results
 | (55) |
Succinctly, the optimal control problem under study is defined by Eqs. (52, 55) and
 | (56) |
 | (57) |
Unless indicated, the initial conditions x(0) = x0 chosen for illustration will be kept fixed at
 | (58) |
A.1. Unbounded controls. The PMP solution.
When the admissible control values are all the real numbers, then the rigorous treatment of this problem along the lines of the PMP is given below. The Hamiltonian H of the problem reads
 | (59) |
which admits a global u-minimization, with explicit forms for the H-minimal control u0 and the minimized Hamiltonian H0, i.e.
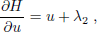 | (60) |
 | (61) |
 | (62) |
leading to the canonical adjoint equations
 | (63) |
Then there should exist real constants a, b such that the optimal costate ?* and control trajectory u have the form
 | (64) |
 | (65) |
 | (66) |
and consequently the dynamic Eqs. (52) can be symbolically integrated to obtain the form of the optimal state trajectories, namely
 | (67) |
Final conditions are compatible (the system is controllable), therefore the value of the constants can be uniquely determined, and the optimal control strategy results
 | (68) |
 | (69) |
In Fig. 1 the optimal control and state trajectories are shown. The unbounded-control solution found above uses (intuitively unexpected) negative control values, i.e. the optimal solution prescribes that the train should be accelerated before beginning the actual braking process. So an obvious question comes to mind: what would the optimal solution be if only (positive) braking is admitted? That will be discussed in detail, but first it will be shown that the solution to the fixed endpoint problem is the limit of flexible-endpoint solutions corresponding to increasing final penalties.

Figure 1: Optimal (PMP) states and control trajectories for the fixed end and unbounded control case.
A.2. Unbounded controls. Flexible endpoints. The PDE solution.
The 'flexible endpoint' problem for the same system and the same Lagrangian replaces the hard constraints in Eqs. (55) by an alternative 'quadratic final penalty' K(x(T)) = x'(T)Sx(T) in the cost objective function, as announced in equation (1). In this example only scalar matrices S = sI will be considered for simplicity. The Riccati matrix P (·) solution to Eq. (9) can be analytically found, having the following components
 | (70) |
and therefore the optimal dynamics (corresponding to the optimal feedback in Eq. (10)) can be integrated and plotted for increasing values of s (see Fig. 2) to ascertain the limiting behavior
 | (71) |

Figure 2: Phase-space optimal trajectories for increasing final penalty. Flexible endpoint, unbounded control case.
where x*(t) denotes the solution to the fixed-end problem resulting from Eqs. (67, 68), i.e.
 | (72) |
Actually, the convergence of solutions from flexible to fixed final-point problems can be proved through the relevant PDE objects as follows. The limiting form of PDEs (40) for s ? 8 is obtained by making as = ßs = 0. Since  (notice that, in general, W ? 0), then the following self-explaining steps lead to the expected result:
(notice that, in general, W ? 0), then the following self-explaining steps lead to the expected result:
 | (73) |
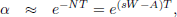 | (74) |
 | (75) |
 | (76) |
In Fig. 2 phase-space trajectories are shown for different values of the parameter s.
A.3.Constrained controls. The case u = 0.
In what follows only nonnegative controls will be allowed (pure braking action), and the initial conditions will remain as in Eq. (58). Since the Hamiltonian has to be minimized at each point, and given that the optimal control begins with a negative value in the unbounded case (or equivalently, ?2(0) > 0), then from Eq. (59) there should exist an initial time interval where the control u assumes the value of the lower bound, namely
 | (77) |
where t is still to be determined. Now, while the control variable is kept at its lower bound, the system evolves along a state trajectory denoted {x(t), t ? [0, t]} . As time increases it is possible to pose successive unbounded control problems starting at x(t) and with optimization horizon [t, T]. By continuity, near t = 0 the optimal solutions to those unbounded control problems will remain negative. If the optimal control for the bounded problem were nontrivial, there should exist a switching time t where the optimal control  for the unbounded problem corresponding to: (i) the remaining horizon {t ? [t, T]} , and (ii) the initial condition x(t), turns nonnegative, i.e.
for the unbounded problem corresponding to: (i) the remaining horizon {t ? [t, T]} , and (ii) the initial condition x(t), turns nonnegative, i.e.  (for alternative arguments leading to the same statement see for instance Alt, 2003; and Bryson and Ho, 1975). Let us assume that such a t ? (0, T] exists, thus during the interval [0, t) the dynamics can be integrated, to obtain
(for alternative arguments leading to the same statement see for instance Alt, 2003; and Bryson and Ho, 1975). Let us assume that such a t ? (0, T] exists, thus during the interval [0, t) the dynamics can be integrated, to obtain
 | (78) |
After time t the optimal control (denoted ut) must be linear, because it behaves as the u0 of a regular problem (the Eqs. (60-63) must be met), i.e. real numbers c, d, m, n exist such that ?t ? [t, T],
 | |
 | (79) |
 | (80) |
and then, after integration, the corresponding state trajectories take the forms
 | (81) |
 |
The concatenation of the lower-bound control followed by 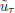 is an admissible control strategy, so the states must match at t = t. In view of Eqs. (78, 81), this amounts to say
is an admissible control strategy, so the states must match at t = t. In view of Eqs. (78, 81), this amounts to say
 | (82) |
 |
Continuity of the control values ut(t) with respect to t follows from the regularity of the unbounded optimal control problem and the smoothness of their governing equations, which implies in this case
 | (83) |
Then, Eqs. (82, 83) require that the unknowns must be solutions to the following pair of equations:
 | (84) |
The final conditions should provide two additional equations to solve the problem. Two cases can in principle be studied:
1. Original (sharp) restrictions: x1(T) = x2(T) = 0. In this case, keeping T = 1, Eq. (81) and the final conditions require
 | (85) |
 |
which, together with Eqs. (83, 84), lead successively to: (t - 1)3 = 0, t = 1, d ? 8, c ? -8. Then, starting at the original initial conditions, only the unfeasible 'infinite braking at the end' solution to the problem is allowed. Thus, the conjecture about the existence of a finite switching time t is wrong in this case.
2. Flexible case:
Let us denote  =
=  (-t, x(t),
(-t, x(t), 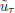 ), where
), where  is the transition map of the system and
is the transition map of the system and 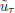 (t)
(t)  c + dt, t ? [0, t), i.e. the continuation of ut to the initial 'saturation' interval (where the optimal control is u(t) = 0). This
c + dt, t ? [0, t), i.e. the continuation of ut to the initial 'saturation' interval (where the optimal control is u(t) = 0). This  results then the proper initial condition of an unbounded-control problem with (full) optimization horizon [0, T] , whose optimal control solution is
results then the proper initial condition of an unbounded-control problem with (full) optimization horizon [0, T] , whose optimal control solution is
 | (86) |
Consequently, the optimal costates  for such unbounded-control problem will obey the HCEs in [0, t] , resulting in
for such unbounded-control problem will obey the HCEs in [0, t] , resulting in
 | (87) |
 | (88) |
Then the costates trajectories ?(·) in Eqs. (79) can be seen as the continuation of trajectories  , i.e. the trajectories
, i.e. the trajectories
 | (89) |
are the optimal costate trajectories corresponding to the initial condition  and control
and control  . This implies, in particular, that at the final time T , the boundary condition for the unbounded problem should be met, precisely
. This implies, in particular, that at the final time T , the boundary condition for the unbounded problem should be met, precisely
 | (90) |
The analysis can then be continued as follows:
 | (91) |
 |
and combining with Eqs. (81, 84), the desired pair of new conditions are obtained:
 | (92) |
 |
At this point it should be noticed that, whatever the final values of the costates, Eqs. (91) already reflect the expected limiting behavior
 |
In order to approximate the fixed-endpoint situation, a large enough value of s should eventually be chosen. Taking for instance s = 100, there exist 5 solutions to Eqs. (92) for (c, d) , but only one of them lies in  , namely c = -13.8331, d = 20.069, t =
, namely c = -13.8331, d = 20.069, t =  = 0.6893; and then, by using Eqs. (91), the final states for this case are obtained: x1(1) = 0.1004, x2(1) = -0.0312. The resulting state and control strategies are depicted in Fig. 3. The train does not arrive to rest, but the solution is more like what can be found in practice: at time T the velocity x2(T) is small enough as to let the train inertially continue from x1(T) to its stoppage without any braking action (u = 0). By using standard mathematical software, analytical expressions for c(s), d(s), t(s) should be obtained, confirming that
= 0.6893; and then, by using Eqs. (91), the final states for this case are obtained: x1(1) = 0.1004, x2(1) = -0.0312. The resulting state and control strategies are depicted in Fig. 3. The train does not arrive to rest, but the solution is more like what can be found in practice: at time T the velocity x2(T) is small enough as to let the train inertially continue from x1(T) to its stoppage without any braking action (u = 0). By using standard mathematical software, analytical expressions for c(s), d(s), t(s) should be obtained, confirming that
 | (93) |

Figure 3: Optimal (PDE) states and control trajectories for the flexible endpoint (s = 100) and bounded control case.
In Fig. A.3. the relations between (some componentes of) x0,  , x,
, x,  , ?,
, ?,  , ut,
, ut,  , are depicted for a fixed value of s. The treatment of this problem along PDE lines will be pursued in subsection B.
, are depicted for a fixed value of s. The treatment of this problem along PDE lines will be pursued in subsection B.

Figure 4: Optimal state x1, costate ?2, and control u trajectories for the bounded-from-below control case, and their hidden parts during saturation.
Comment: The smallest absolute velocity that admits pure braking. In the regular (unbounded) linear-quadratic case the solutions to optimal control problems depend continuously on the parameters (initial and final conditions, matrix coefficients, final penalties, and the like). It is important to ascertain this continuous behavior in the non regular situation, as an extension of the arguments used above. For instance, the influence of the lower bound on the structure of the optimal control also varies continuously with other parameters. In this subsection it will be shown that not all initial conditions require calculation of broken-line trajectories and their corresponding switching times in order to avoid negative control values. Clearly, absolute values for the initial velocity  will lead to acceleration periods (with u < 0). But, let us explore whether there exists a smallest absolute value ? for the initial velocity, i.e.
will lead to acceleration periods (with u < 0). But, let us explore whether there exists a smallest absolute value ? for the initial velocity, i.e.
 | (94) |
such that the optimal (unbounded) control results always nonnegative. Using the notation in Subsection A.1. and supposing as a limiting condition that the control starts at its bound-value, then
 | (95) |
and the following relations become valid from state and costate dynamics:
 | |
 | |
 | (96) |
 | |
 |
Now, in order to reach the final target x1(1) = x2(1) = 0, the unknowns should be
 | (97) |
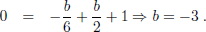 |
This gives the desired bound on the initial velocities for pure braking optimal control, namely,
 |
and the optimal control
 |
requires half the slope than the case with  = 1. For
= 1. For  = ? the optimal control will be always nonnegative (pure braking), and for
= ? the optimal control will be always nonnegative (pure braking), and for  < ? there will be an initial acceleration period.
< ? there will be an initial acceleration period.
B. Approximating the original problem via the PDE solutions.
In subsection A it became clear that meeting sharp restrictions on final states with PMP is not practicable when only nonnegative controls and initial velocities with smaller absolute values than ? are allowed. Then an approximate solvable problem was sought and analytically solved. The alternative was found by making the endpoint flexible, precisely by imposing a quadratic final penalty on the states. In the literature (see Alt (2003), Bryson and Ho (1975) and the references therein) little theoretical advances have been made in the treatment of these situations, other than including extra Lagrange multipliers to take into account the control bounds (a major inconvenience of such an approach is the appearing of inequalities, difficult to handle analytically).
From now on the same flexible-endpoint boundedcontrol linear-quadratic problem above will be treated along PDE lines. Notice however that all relevant equations in this subsection are expressed in terms of the auxiliary matrices solving the main PDEs, and therefore these results are applicable to general LQR problems. It will be assumed that a reasonably high value of s has been fixed. It was shown that an intermediate time t ? (0, 1) exists such that the optimal control strategy is of the form
 | (98) |
where ub(t) is the control assuming the bound value, and us,t(t) is the optimal control for the free-endpoint problem corresponding to the horizon T - t = 1 - t, final penalization  , and initial condition
, and initial condition
 | (99) |
Then, according to Eq. (50),
 | (100) |
 | |
 |
where the subscript  denotes 'the second component'of the vector inside the brackets.
denotes 'the second component'of the vector inside the brackets.
Using Eq. (101) for t = t, and noticing that u(t) = ub(t) = 0 ? t ? [0, t) implies that x(t) = eAtx0, then the matching condition reads
 | (101) |
 |
The value of t is the only unknown in Eq. (102). Assuming that a(T, S), ß(T, S) have been calculated for a wide range of (T, S)-values, then the problem of finding t may reduce to find the zero of the function ûs : [0, T] ?  defined by
defined by
 | (102) |
In Fig. 5 a plot of the curve ûs(t) obtained by the PDE method is shown. It can be seen that the crosspoint is very close to t = 0.6892 as predicted analytically. The curve is an isocline (s = 100) for the controls evaluated at time t and present state value eAtx0. Each control value ûs(t) is optimal at time t for an optimal control problem with: (i) the 'initial' state eAtx0 (no braking has been applied before t), (ii) the optimization horizon T - t, and (iii) the final penalty coefficient s.

Figure 5: Isocline (PDE, s = 100) for the controls evaluated at time t and present state value eAtx0, each one optimal with respect to the horizon T - t.
Some numerical calculations have been performed to test these results. Figure 5 also illustrates other isoclines for different values of s and their corresponding switching times t(s), all constructed from PDEs' solutions. Figure 6 shows the relative deviations in states and control trajectories generated by the PDE method (Eqs. (101, 102) and numerical integration of Eqs. (52)), from those corresponding to the analytical solution of the problem Eqs. (78-81), for s = 100 and times greater than the relevant switching time t. An empirical test for optimality can be observed in Table 1, where total and partial costs for several control variations have been reported. The names given in Table 1 for the control variations are self-explaining when associated to their graphical versions shown in Fig. 7, except for the 'shortsighted' curve. That label has been assigned to the strategy consisting in applying the saturation control u(t) = 0 up to the time (t = t0 =  ) where the optimal control u*(t) for the fixed-end problem stops being negative (see Fig. 1 and Eq. (69)), and then continue by using u(t) = u*(t) for t ? [t0, T].
) where the optimal control u*(t) for the fixed-end problem stops being negative (see Fig. 1 and Eq. (69)), and then continue by using u(t) = u*(t) for t ? [t0, T].

Figure 6: Relative errors in calculations of x and u from the numerical solutions of the first orders PDEs, with respect to the analytical solution of the problem.

Table 1: Costs and final states' values and final for the solution strategy to the optimal control problem with a unique switching point, and for some control variations.

Figure 7: Variations to the optimal control strategy with a unique switching time t, used for cost comparisons.
C. Extension to the treatment of both lower and upper bounds in control values.
Let us consider now the existence of two bounds on control values, for instance 0 = u(t) = D. In case the control is saturated at both constrains, that will happen at least for two switching times t1, t2. Assume 0 < t1 < t2 < T, and applying the same arguments than before to the example at hand, the three emerging subintervals can be analyzed as follows:
(i) For t ? [0, t1], u = 0. This first part is analogous to the case with only the lower bound at u = 0, so the Eqs. (78): x2(t) = - 1, x1(t) = 1 - t, remain valid.
(ii) For t ? [t1, t2], the optimal control will be a linear function of t, since in this subinterval the problem has a regular structure. Then, after writing
 | (103) |
and using  ,
,  , z, w to denote unknown constants, relations between the states' trajectories and the boundary conditions can be obtained by direct integration, namely
, z, w to denote unknown constants, relations between the states' trajectories and the boundary conditions can be obtained by direct integration, namely
 | (104) |
 | (105) |
 | (106) |
 | (107) |
Using the same arguments, the costates and control trajectories become
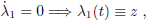 | (108) |
 | (109) |
 | (110) |
and therefore, at the next switching time the following relations must be true
 | (111) |
 | (112) |
 | (113) |
 | (114) |
As shown when u was only bounded from below, the condition for the final instant of this period should be
 | (115) |
where the expression for P(t2) can be obtained from Eq. (70). Then, from Eqs. (103-115) the values of the remaining unknowns t1 and t2 can be obtained:
| t1 = 0.689277, t2 = 0.938417, | (116) |
which shows that t1 is the same as the t previously found, and also that the second switching time t2 verifies ut1(t2) = D , where ut1 must be interpreted as in Eq. (80) for the lower-bound case. The calculation of t2, assuming t1 is known, is also possible from the solutions to the PDEs. In fact, it reduces to solve
 | (117) |
 |
with the provision of replacing x(t2) by the optimal final state for an horizon of duration t2 - t1 and initial condition x(t1), i.e.
 | (118) |
This can be simplified by using the properties of matrix a as the fundamental matrix of the system
 | (119) |
(see Eqs. (12, 19)), i.e.
 | |
 | (120) |
Then the appropriate equation to solve for t2 is
 | (121) |
The value t2 = 0.938417 found this way coincides with the one obtained analytically (see also Fig. 9).

Figure 9: Second switching times t2 and corresponding optimal control strategies, for different final penalty coefficients s.
(iii) Finally, for time t ? [t2, T] = [t2, 1],
 |
Summarizing, the switching times can be obtained from the PDE method by solving algebraic equations like (102) and (121). This in principle may be done numerically, since all values for matrices a, ß are stored. During the 'regular' subintervals the optimal feedback is also generated from the PDEs' solutions as required by Eq. (29). Results are illustrated in Fig. 8. The empirical optimality comparisons for the two-bounds case are condensed in Table 2 and Fig. 10. The sisoclines for determining the switching time t2 from PDE's solutions are depicted in Fig. 9.

Figure 8: Optimal states and control trajectories when lower and upper constraints are present.

Table 2: Costs and final states' values for the solution strategy to the optimal control problem with two switching points, and for some control variations.

Figure 10: Variations to the optimal control strategy with two switching times (t1,t2), used for cost comparisons.
V. CONCLUSIONS
The first-order PDEs for the final states and initial costates of optimal control regular problems have been proved useful in non regular and fixed-final-state situations. Solutions to these PDEs allow to transform the classical two-point boundary-value ODE system associated with the Hamiltonian formulation, into an initial-value set-up with unique solution. In the LQR context, two matrix, quasilinear, first-order PDEs for auxiliary variables a, ß were here made explicit, and their treatment was extended for the first time to a general final coefficient matrix S. From their solutions, the missing boundary conditions can be effectively recovered after simple manipulations. Actually, the auxiliary variables are found for a two-parameter family of LQR problems posed for fixed plant dynamics and trajectory costs, but with variable final penalties and horizon spans. This immersion allows a whole range of (T, S)-problems to be assessed by looking at the final reachable state ?(T, S) and the associated marginal cost s(T,S).
It has been found that the solution to a twice-infinite family of LQR problems requires little numerical effort, roughly similar to the one involved in running the associated DRE for just one individual situation. The solution for a range of (T, S)-values provides design information, useful when flexible choice of the parameters to improve performance is required. It is even more important the fact that these solutions can also be used to find the optimal strategy when the admissible control values are bounded. The eventual switching times ti, i = 1, 2,..., can either be: (i) calculated a priori (off-line) by solving algebraic equations like (102, 121) associated with all control saturation possibilities, or (ii) detected on-line by continuously evaluating the right-hand-side-members of the same equations until they reach/leave the saturation conditions.
The novel PDEs were developed and proved for flexible-final-state problems with a quadratic final penalty of the type (x(T) -  )' S (x(T) -
)' S (x(T) -  ) , were
) , were  is a target. But when S = sI, s = 0, then for s ? 8 their solutions approach that of the corresponding fixed-final-state problem (with condition x(T) =
is a target. But when S = sI, s = 0, then for s ? 8 their solutions approach that of the corresponding fixed-final-state problem (with condition x(T) =  ). Therefore solutions to 'flexible' problems can be regarded as approximations to the 'fixed endpoint' situation. This turns out to be relevant in solving non-regular (here just bounded-control) problems. It has been shown through the chosen example that the limiting, fixed endpoint solution for bounded control may not exist (or may be not realizable in practical terms), while the flexible approximations give appropriate engineering answers.
). Therefore solutions to 'flexible' problems can be regarded as approximations to the 'fixed endpoint' situation. This turns out to be relevant in solving non-regular (here just bounded-control) problems. It has been shown through the chosen example that the limiting, fixed endpoint solution for bounded control may not exist (or may be not realizable in practical terms), while the flexible approximations give appropriate engineering answers.
REFERENCES
1. Abraham, R. and J. E. Marsden, Foundations of Mechanics, Benjamin / Cummings, Reading, Massachusetts, second edition (1978). [ Links ]
2. Agrachev, A. and Y. Sachkov, Control Theory from the Geometric Viewpoint, Springer-Verlag, Berlin-Heidelberg (2004). [ Links ]
3. Alt, W., "Approximation of optimal control problems with bound constraints by control parameterization," Control and Cybernetics, 32, 451-472 (2003). [ Links ]
4. Bellman, R. and R. Kalaba, "A note on hamilton's equations and invariant imbedding," Quarterly of Applied Mathematics, XXI, 166-168 (1963). [ Links ]
5. Bernhard, P., Introducción a la Teoría de Control Óptimo, Instituto de Matemática "Beppo Levi", Cuaderno Nro. 4, Rosario, Argentina (1972). [ Links ]
6. Bryson, A. J. and Y. Ho, Applied Optimal Control, John Wiley and Sons, New York, revised printing edition (1975). [ Links ]
7. Costanza, V., "Finding initial costates in finitehorizon nonlinear-quadratic optimal control problems," Optimal Control Applications and Methods, 29, 225-242 (2008a). [ Links ]
8. Costanza, V., "Regular optimal control problems with quadratic final penalties," Revista de la Uni´on Matem´atica Argentina, 49, 43-56 (2008b). [ Links ]
9. Costanza, V., "Optimal two-degrees-of-freedom control of nonlinear systems," Proceedings of the XIII Workshop on Information Processing and Control, Rosario-Argentina (2009). [ Links ]
10. Costanza, V. and C. E. Neuman, "Optimal control of nonlinear chemical reactors via an initial-value hamiltonian problem," Optimal Control Applications and Methods, 27, 41-60 (2006). [ Links ]
11. Costanza, V. and C. E. Neuman, "Partial differential equations for missing boundary conditions in the linear-quadratic optimal control problem," Latin American Applied Research, 39, 207-212 (2009). [ Links ]
12. Costanza, V. and P. S. Rivadeneira, "Finite-horizon dynamic optimization of nonlinear systems in real time," Automatica, 44, 2427-2434 (2008). [ Links ]
13. Costanza, V., P. S. Rivadeneira, and R. D. Spies, "Equations for the missing boundary values in the Hamiltonian formulation of optimal control problems," Journal of Optimization Theory and Applications, (To appear) (2011). [ Links ]
14. Howlett, P., P. Pudney, and X. Vu, "Local energy minimization in optimal train control," Automatica, 45, 2692-2698 (2009). [ Links ]
15. Kalman, R. E., P. L. Falb, and M. A. Arbib, Topics in Mathematical System Theory, MacGraw-Hill, New York (1969). [ Links ]
16. Pontryagin, L. S., V. G. Boltyanskii, R. V. Gamkrelidze, and E. F. Mischenko, The Mathematical Theory of Optimal Processes, Wiley, New York (1962). [ Links ]
17. Sontag, E. D., Mathematical Control Theory, Springer, New York (1998). [ Links ]
Received: March 25, 2010
Accepted: January 17, 2011
Recommended by subject editor: José Guivant













