ARTICLES

Soret and dufour effects in a mixed convection couple stress fluid with heat and mass fluxes

D. Srinivasacharya and K. Kaladhar

Department of Mathematics, National Institute of Technology, Warangal-506004, India
dsc@nitw.ac.in, dsrinivasacharya@yahoo.com

Abstract — An analysis is presented to investigate the Soret and Dufour effects on the mixed convection heat and mass transfer along a semi-infinite vertical plate embedded in a couple stress fluid with flux distributions. The governing non-linear partial differential equations are transformed into a system of ordinary differential equations using similarity transformations and then solved numerically. Profiles of dimensionless velocity, temperature and concentration are shown graphically for various values of Dufour number, Soret number and Couple stress parameter.

Keywords — Mixed convection; Couple stress fluid; Soret and Dufour effect; Heat and mass transfer.

I. INTRODUCTION

The analysis of mixed convection boundary layer flow along a vertical plate embedded in viscous fluid has received considerable theoretical and practical interest. The phenomenon of mixed convection occurs in many technical and industrial problems such as electronic devices cooled by fans, nuclear reactors cooled during an emergency shutdown, a heat exchanger placed in a low-velocity environment, solar collectors and so on. Several authors have studied the problem of mixed convection about different surface geometries. When heat and mass transfer occur simultaneously in a moving fluid, the relations between the fluxes and the driving potentials are of a more intricate nature. It has been observed that an energy flux can be generated not only by temperature gradients but also by concentration gradients. The energy flux caused by a concentration gradient is termed the diffusion-thermo (Dufour) effect. On the other hand, mass fluxes can also be created by temperature gradients and this embodies the thermal-diffusion (Soret) effect. In most of the studies related to heat and mass transfer process, Soret and Dufour effects are neglected on the basis that they are of a smaller order of magnitude than the effects described by Fourier and Fick's laws. But these effects are considered as second order phenomena and may become significant in areas such as hydrology, petrology, geosciences, etc. The Dufour effect was recently found to be of order of considerable magnitude such that it cannot be neglected (Eckeret and Drake, 1972). Dursunkaya and Worek (1992) studied diffusion-thermo and thermal-diffusion effects in transient and steady natural convection from a vertical surface, whereas Kafoussias and Williams (1995) presented the same effects on mixed convective and mass transfer transfer steady laminar boundary layer flow over a vertical flat plate with temperature dependent viscosity. Postelnicu (2004) studied numerically the influence of a magnetic field on heat and mass transfer by natural convection from vertical surfaces in porous media considering Soret and Dufour effects. Both free and forced convection boundary layer flows with Soret and Dufour have been addressed by Abreu et.al., (2006). Alam and Rahman (2006) have investigated the Dufour and Soret effects on mixed convection flow past a vertical porous flat plate with variable suction. The effect of Soret and Dufour parameters on free convection heat and mass transfers from a vertical surface in a doubly stratified Darcian porous medium have been reported by Lakshmi Narayana and Murthy (2007). Recently, Lakshmi Narayana and Sibanda (2010) studied Soret and Dufour effects on free convection along a vertical wavy surface in a fluid saturated Darcy porous medium.

It is known that many of the industrially and technologically important fluids behave like a non-Newtonian fluid. The effects of heat and mass transfer in non-Newtonian fluid also have great importance in engineering applications like the thermal design of industrial equipment dealing with molten plastics, polymeric liquids, foodstuffs, or slurries. Several investigators have extended many of the available convection heat and mass transfer problems to include the non-Newtonian effects. Dufour and Soret effects on heat and mass transfer in a non-Newtonian micropolar fluid in a horizontal channel have been presented by Awad and Sibanda (2010). The couple stress fluid theory developed by Stokes (1966) represents the simplest generalization of the classical viscous fluid theory that sustains couple stresses and the body couples. The important feature of these fluids is that the stress tensor is not symmetric and their accurate flow behavior cannot be predicted by the classical Newtonian theory. The main effect of couple stresses will be to introduce a size dependent effect that is not present in the classical viscous theories. The fluids consisting of rigid, randomly oriented particles suspended in a viscous medium, such as blood, lubricants containing small amount of polymer additive, electro-rheological fluids and synthetic fluids are examples of these fluids. Application of the couple stress model to biomechanics problems has been proposed in the study of peristaltic transport by Srivastava (1986), Shehawey and Mekheimer (1994) and blood flow in the microcirculation by Pal et al., (1988). In lubrication problems many authors have investigated the couple stress effects on different lubrication problems (Chiang et al.,, 2004; Naduvinamani et al., 2005; Chiang-Jian and Chen et al., 2008; Lu and Lin, 2007).

The objective of this paper is to investigate the Dufour and Soret effects on steady combined free-forced convective and mass transfer flow past a semi-infinite vertical flat plate in couple stress fluid. The Keller-box method (Cebeci and Bradshaw, 1988) is employed to solve the nonlinear problem. The effects of couple stress fluid parameter, Soret and Dufour numbers are examined and are displayed through graphs.

II. MATHEMATICAL FORMULATION

Consider a two-dimensional mixed convective heat and mass transfer along a semi-infinite vertical plate embedded in a free stream of couple stress fluid with velocity u8, temperature T8 and concentrations C8.

Choose the coordinate system such that x-axis is along the vertical plate and y-axis normal to the plate. The plate is maintained at uniform and constant heat and mass fluxes qw and mw respectively. In addition, the Soret and Dufour effects are considered (Kafoussias and Williams, 1995). The flow configuration and the coordinates system are shown in Fig. 1

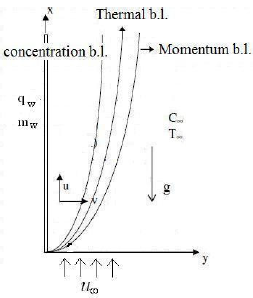
Figure 1: Physical model and coordinate system.

Using Boussinesq and boundary layer approximations, the governing equations for the couple stress fluid are given by

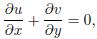	(1)
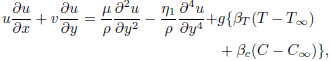	(2)
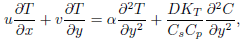	(3)
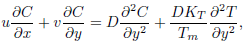	(4)

where u, v are the velocity components in the x and y directions respectively, µ is the coefficient of viscosity, g is the acceleration due to gravity, ? is the density, ß_T is the coefficient of thermal expansion, ß_c is the coefficient of solutal expansion, a is the thermal diffusivity, D is the mass diffusivity, C_p is the specific heat capacity, C_s is the concentration susceptibility, T_m is the mean fluid temperature, K_T is the thermal diffusion ratio and ?₁ is the couple stress fluid parameter. The last terms on the right-hand side of the energy equation (3) and concentration equation (4) signifies the Dufour (diffusion-thermo) effect and the Soret (thermal-diffusion) effect, respectively.

The boundary conditions are

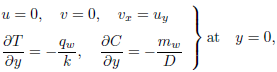	(5a)
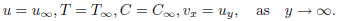	(5b)

Introducing the following similarity transformations

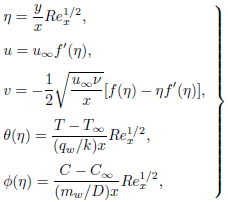(6)

in Eqs. (1) -(4), we get the following nonlinear system of differential equations

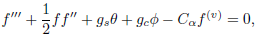	(7)
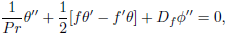	(8)
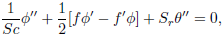	(9)

where primes denote differentiation with respect to ?, 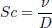is the Schmidt number, 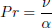is the Prandtl number, 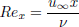is the local Reynolds number, 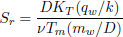is the Soret number, 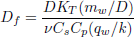is the Dufour number, 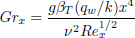is the local temperature Grashof number, 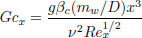is the local mass Grashof number, 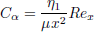is the couple stress parameter, 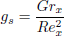is the temperature buoyancy parameter and 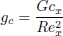is the mass buoyancy parameter. The term 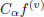in (7) gives the effect of couple stresses. Hence, as C_a increases, the effect of couple stresses increase.

Boundary conditions (17) in terms of f, ? and become

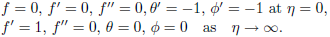(10)

III. METHOD OF SOLUTION

The flow equation (7) together with the energy and concentration equations (8) and (9), constitute non-linear nonhomogeneous differential equations for which closed-form solutions cannot be obtained. Hence the governing equations (7) -(9) are solved numerically using the Keller-box implicit method (Cebeci and Bradshaw, 1988). This method has been proven to be adequate and give accurate results for boundary layer equations.

To solve the boundary value problems by the Keller box method Eqs. (7) -(9) are first converted into a system of first order differential equations as follows:

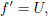	(11a)
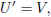	(11b)
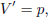	(11c)
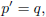	(11d)
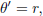	(11e)
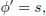	(11f)
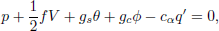	(11g)
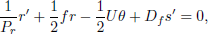	(11h)
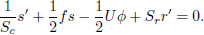	(11i)

In terms of the new dependent variables, the boundary conditions (10) are given by

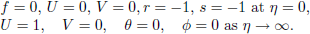(12)

The derivatives are approximated by centereddifference gradients and averages centered at the midpoints of the net, defined by

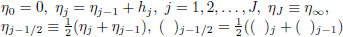(13)

where h_j is ?? the spacing.

Equation (11) then becomes

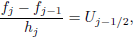	(14a)
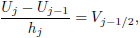	(14b)
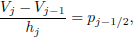	(14c)
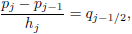	(14d)
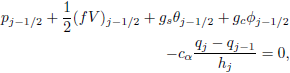	(14e)
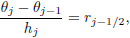	(14f)
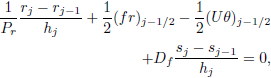	(14g)
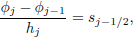	(14h)
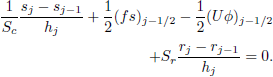	(14i)

Equations (14) are nonlinear algebraic equations and therefore have to be linearized before the factorization scheme can be used. To linearize the nonlinear system of equations (14), using Newton's method, we introduce the following iterates

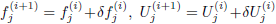etc.

(15)

for all dependent variables. By substituting these expressions into Eq. (14) and dropping the quadratic and higher-order terms in 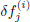, , 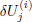etc., the following linear tridiagonal system of equations is obtained (the superscript i is dropped for simplicity):):

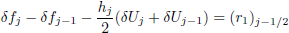	(16a)
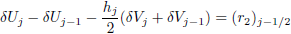	(16b)
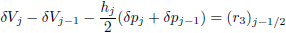	(16c)
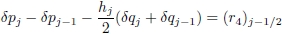	(16d)
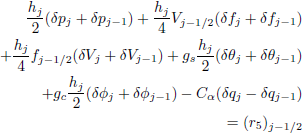	(16e)
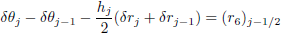	(16f)
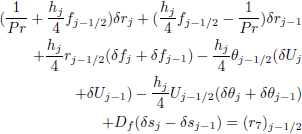	(16g)
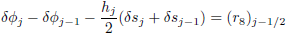	(16h)
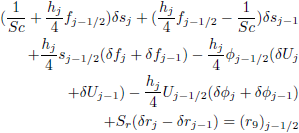	(16i)

here

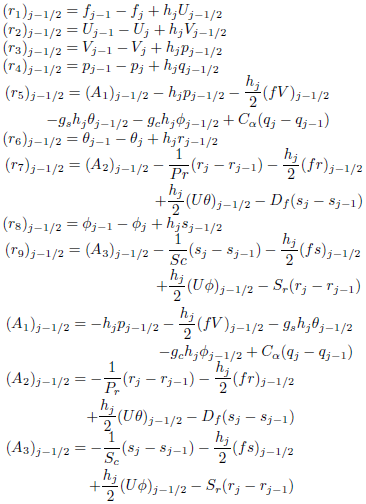The boundary conditions (12) become

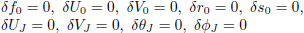(17)

The linearized difference equations (16) can be solved using a block-matrix version of the Thomas algorithm; the details of the computational procedure have been discussed further in the book by Cebecci and Bradshow (1988), since the system has block-tridiagonal structure. Commonly, the blocktridiagonal structure consists of variables or constants, but here an interesting feature can be observed that it consists of block matrices.

present method has a second-order accuracy, is unconditionally stable and is easy to be programmed, thus making it highly attractive for production use.

In the present study, the boundary conditions for ? at 8 are replaced by a sufficiently large value of ? where the velocity approaches one and temperature and concentration approach zero. The value of ?₈ is taken as 6. In order to see the effects of step size (?_?) we executed the code for our model with two different step sizes as ?_? = 0.01 and ?_? = 0.001 depending on the values of the parameters considered and in each case we found very good agreement between them. a uniform grid of ?? = 0.01 was found to be satisfactory for a convergence criterion of 10^-6, which gives accuracy to four decimal places, in nearly all cases.

IV. RESULTS AND DISCUSSION

In order to study the effects of couple stress fluid parameter C_a, Soret number S_r and Dufour number D_f explicitly, computations were carried out for the cases of Pr = 0.71(air), Sc = 0.22(hydrogen at 25°C and 1 atmosphere pressure), g_s = 1.0 and g_c = 0.1. The values of Soret number S_r and Dufour number D_f are chosen in such a way that their product is constant according to their definition provided that the mean temperature T_m is kept constant (Kafoussias and Williams, 1995).

Figure 2 displays the non-dimensional velocity for different values of Soret number S_r and Dufour number D_f with fixed value of couple stress fluid paramter C_a. It can be observed from this figure that the velocity of the fluid increases with the increase of Dufour number (or decrease of Soret number). The dimensionless temperature for different values of Soret number S_r and Dufour number D_f for C_a = 1.0 is shown in Fig. 3. It is clear that the temperature of the fluid increases with the increase of Dufour number (or de-crease Soret number). Figure 4 shows the dimensionless concentration for different values of Soret number S_r and Dufour number D_f for C_a = 1.0. It is seen that the concentration of the fluid increases with decrease of Dufour number (or increase of Soret number).

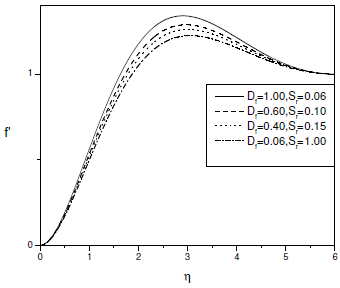
Figure 2: Velocity profile for different values of D_f, S_r at C_a = 1.0,g_s = 1.0,g_c = 0.10

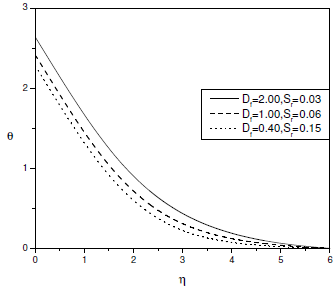
Figure 3: Temperature profile for different values of D_f, S_r at C_a = 1.0,g_s = 1.0,g_c = 0.10

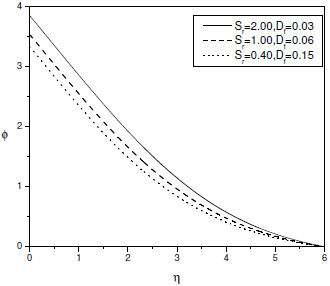
Figure 4: Concentration profile for different values of D_f, S_r at C_a = 1.0,g_s = 1.0,g_c = 0.10

In Figs. 5-7, the effects of the couple stress parameter C_a on the dimensionless velocity, temperature and concentration profiles are presented for fixed values of Soret and Dufour numbers. As C_a increases, it can be observed from Fig. 5 that the maximum velocity decreases in amplitude and the location of the maximum velocity moves far away from the wall. It is clear from Fig. 6 that the temperature increases with the increase of couple stress fluid parameter C_a. It can be seen from Fig. 7 that the concentration of the fluid increases with the increase of couple stress fluid parameter C_a. It can be noted that the velocity in case of couple stress fluid is less than that of a Newtonian fluid case. Temperature and concentration in case of couple stress fluid are more than that of viscous fluid. Hence, the presence of couple stresses in the fluid decreases the velocity and increases temperature and concentration.

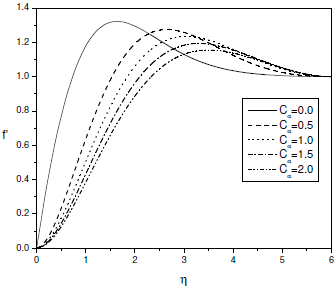
Figure 5: Velocity profile for different values of C_a at g_s = 1.0,g_c = 0.10, D_f = 0.03, S_r = 2.0

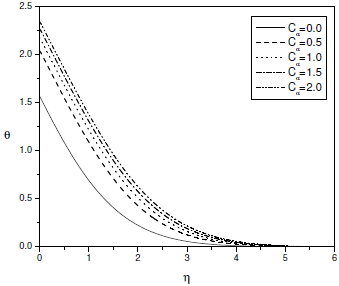
Figure 6: Temperature profile for different values of C_a at g_s = 1.0,g_c = 0.10, D_f = 0.03, S_r = 2.0

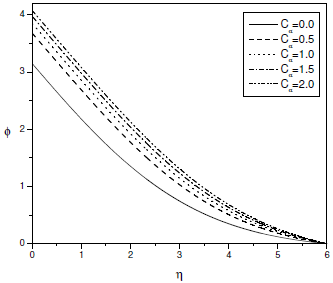
Figure 7: Concentration profile for different values of C_a at g_s = 1.0,g_c = 0.10, D_f = 0.03, S_r = 2.0

V. CONCLUSIONS

In this paper, the Dufour and Soret effects on steady mixed convective heat and mass transfer flow along a semi-infinite vertical plate in a couple stress fluid has been studied numerically. Using similarity transformations, the governing equations have been transformed into non-linear ordinary differential equations. The similarity solutions are obtained numerically applying Keller-Box method. From the present study we observe that

1. The velocity and the temperature of the fluid increases with the increase of Dufour number (or decrease of Soret number) and with decrease of Dufour number (or increase of Soret number) the concentration of the fluid increases.
2. The presence of couple stresses in the fluid de-creases the velocity and increases temperature and concentration.

REFERENCES
1. Abreu, C.R.A., M.F. Alfradique and A.T. Silva, "Boundary layer flows with Dufour and Soret effects: I: Forced and natural convection," Chemical Engineering Science, 61, 4282-4289 (2006).         [ Links ]
2. Alam, M.S. and M.M. Rahman, "Dufour and Soret effects on mixed convection flow past a vertical porous flat plate with variable suction," Nonlinear analysis: Modeling and Control, 11, 3-12 (2006).         [ Links ]
3. Awad, F. and P. Sibanda, "Dufour and Soret effects on heat and mass transfer in a micropolar fluid in a horizontal channel," WSEAS Transactions on Heat and Mass Transfer, 5, 165 -177 (2010).         [ Links ]
4. Cebeci, T. and P. Bradshaw, "Physical and Computational Aspects of Convective Heat Transfer," Springer-Verlag, New York, (1988).         [ Links ]
5. Chiang, H-L., C-H. Hsu and J-R. Lin, "Lubrication performance of finite journal bearings considering effects of couple stresses and surface roughness," Tribol. Int, 37, 297-307 (2004).         [ Links ]
6. Dursunkaya, Z. and W.M. Worek, "Diffusion-thermo and thermal diffusion effects in transient and steady natural convection from a vertical surface," Int. J. Heat Mass Transfer, 35 , 2060-2065 (1992).         [ Links ]
7. Eckeret, E.R.G. and R.M. Drake, "Analysis of heat and mass transfer," McGraw Hill,Newyark, (1972).         [ Links ]
8. Chang-Jian, C-W. and Chao-Kuang Chen, "Chaos and bifurcation of a flexible rotor supported by porous squeeze couple stress fluid film journal bearings with non-linear suspension," Chaos, Solitons Fractals, 35, 358-375 (2008).         [ Links ]
9. Kafoussias, N.G. and N.G. Williams, "Thermal-diffusion and diffusion-thermo effects on mixed free-forced convective and mass transfer boundary layer flow with temperature dependent viscosity," Int. J. Engng. Sci., 33 , 1369-1384 (1995).         [ Links ]
10. Kafoussias N.G, "Local similarity Solution for Cmbined Free-forced Convective and Mass Transfer Flow Past a Semi-infinite Vertical Plate," Int. J. Energy Res., 14, 305-309 (1990).         [ Links ]
11. Lu, R-F. and J-R. Lin, "A theoretical study of combined effects of non-Newtonian rheology and viscositypressure dependence in the sphere-plate squeeze-film system," Tribol. Int., 40, 125-131 (2007).         [ Links ]
12. Lakshmi Narayana, P.A. and P.V.S.N. Murthy, "Soret and Dufour effects in a doubly stratified Darcy porous medium," Journal of Porous Media, 10, 613-624 (2007).         [ Links ]
13. Lakshmi Narayana, P.A. and P. Sibanda, "Soret and Dufour effects on free convection along a vertical wavy surface in a fluid saturated Darcy porous medium," Int. J. of Heat and Mass Transfer, 53, 3030 -3034 (2010).         [ Links ]
14. Naduvinamani, N.B., P.S. Hiremath and G. Gurubasavaraj, "Effect of surface roughness on the couplestress squeeze filmbetween a sphere and a flat plate," Tribol. Int., 38 , 451-458 (2005).         [ Links ]
15. Pal, D., N. Rudraiah and R. Devanathan, "A couple stress model of blood flow in the microcirculation," Bull. Math. Biol, 50, 329-344 (1988).         [ Links ]
16. Postelnicu, A., "Influence of a magnetic field on heat and mass transfer by natural convection from vertical su-faces in porous media considering Soret and Dufour effects," Int. J. of Heat Mass Transfer, 47, 1467-1475 (2004).         [ Links ]
17. Shehawey, E.F.E. and K.S. Mekheimer, "Couple-stresses in peristaltic transport of fluids," J. Phys. D. Appl. Phys, 27, 1163-1170 (1994).         [ Links ]
18. Srivastava, L.M., "Peristaltic transport of a couple-stress fluid," Rheol. Acta 25, 294, 638-641 (1986).         [ Links ]
19. Stokes, V.K., "Couple Stresses in fluid," The physics of fluids, 9, 1709-1715 (1966).         [ Links ]

Received: August 13, 2010
Accepted: January 17, 2011
Recommended by subject editor: Walter Ambrosini