Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. vol.41 no.4 Bahía Blanca oct. 2011
ARTICLES
Using hybrid parallel programming techniques for the computation, assembly and solution stages in finite element codes
R.R. Paz, M.A. Storti, H.G. Castro and L.D. Dalcín
Centro Internacional de Métodos Computacionales en Ingeniería (CIMEC), Instituto de Desarrollo Tecnológico para la Industria Química (INTEC), CONICET, Universidad Nacional del Litoral (UNL). Santa Fe, Argentina.
{rodrigop\mstorti\dalcinl}@intec.unl.edu.ar
Grupo de Investigación en Mecánica de Fluidos, Universidad Tecnológica Nacional, Facultad Regional Resistencia, Chaco,
Argentina. castrohgui@gmail.com
Abstract The so called "hybrid parallelism paradigm", that combines programming techniques for architectures with distributed and shared memories using MPI (Message Passing Interface) and OpenMP (Open Multi-Processing) standards, is currently adopted to exploit the growing use of multi-core computers, thus improving the efficiency of codes in such architectures (several multi-core nodes or clustered symmetric multi-processors (SMP) connected by a fast net to do exhaustive computations).
In this paper a parallel hybrid finite element code is developed and its performance is evaluated, using MPI for communication between cluster nodes and OpenMP for parallelism within the SMP nodes. An efficient thread-safe matrix library for computing element/cell residuals (or right hand sides) and Jacobians (or matrices) in FEM-like codes is introduced and fully described. The cluster in which the code was tested is the CIMEC's 'Coyote' cluster, which consists of eight-core computing nodes connected through Gigabit Ethernet.
Keywords Finite Elements; MPI; OpenMP; PETSc; Hybrid programming; Matrix Library.
I. INTRODUCTION
A variety of engineering applications and scientific problems related to Computational Mechanics (CM) area, and particularly in the Computational Fluid Dynamics (CFD) field, demand high computational resources (Sonzogni et al., 2002). A great effort has been made over the years in order to obtain high quality solutions (Paz et al., 2006) for large-scale problems in realistic time (Behara and Mittal., 2009) using many different computing architectures (e.g., vector processors, distributed and shared memories, graphic process units or GPGPU's).
Symmetric multi-processors (SMP) involve a hardware architecture with two or more identical processors connected to a single shared main memory. Other recent computing systems might use Non-Uniform Memory Access (NUMA). NUMA dedicates different memory banks to different processors; processors may access local memory quickly. Despite the differences with NUMA architectures, this work will use the term SMP in a broader sense to refer to a general many-processor many-core single-memory computing machine.
Since SMP have spread out widely in conjunction with high-speed network hardware, using SMP clusters have become attractive for high-performance computing. To exploit such computing systems the tendency is to use the so called hybrid parallelism paradigm that combines programming techniques for architectures with distributed and shared memory, often using MPI and OpenMP standards (Jost and Jin., 2003). The hybrid MPI/OpenMP programming technique is based on using message passing for coarse-grained parallelism and multi-threading for fine-grained parallelism.
The MPI programming paradigm defines a high-level abstraction for fast and portable inter-process communication and assumes a local/private address space for each process. Applications can run in clusters of (possibly heterogeneous) workstations or dedicated nodes, SMP machines, or even a mixture of both. MPI hides all the low-level details, like networking or shared memory management; simplifying development and maintaining portability, without sacrificing performance (see Section V.B).
Although message passing is the way to communicate between nodes, it could not be an efficient resource within an SMP node. In shared memory architectures, parallelization strategies that use OpenMP standard could provide better performances and efficiency in parallel applications. A combination of both paradigms within an application that runs on hybrid clusters may provide a more efficient parallelization strategy than those applications that exploit the features of pure MPI.
This paper is focused on a mixed MPI and OpenMP implementation of a finite element code for scalar PDE's and discusses the benefits of developing mixed mode MPI/OpenMP codes running on Beowulf clusters of SMP's. To address these objectives, the remainder of this paper is organized as follows. Section II provides a short description and comparison of different characteristics of OpenMP and MPI paradigms. Section III introduces and describes an efficient thread-safe matrix library called Fast-Mat for computing element residuals and Jacobians in the context of multi-threaded finite element codes. Section IV discusses the implementation of mixed (hybrid) mode application and describes a number of situations where mixed mode programming is potentially beneficial. Section V presents the implementation of an hybrid application such as advective-diffusive partial differential equation. Several tests are performed on a cluster of SMP's and on single SMP workstations (Intel Xeon E54xx-series and i7 architectures) comparing and contrasting the performance of the FEM code. The results demonstrate that this style of programming may increase the code performance. This improvement can be achieved by taking into account a few rules of thumb depending on the application at hand. Concluding remarks are given in section VI.
II AN OVERVIEW OF MPI AND OPENMP
A. MPI
MPI, the Message Passing Interface (MPI, 2010), is a standardized and portable message-passing system designed to function on a wide variety of parallel computers. The standard defines the syntax and semantics of library routines (MPI is not a programming language extension) and allows users to write portable programs in the main scientific programming languages (Fortran, C and C++). The MPI programming model is a distributed memory model with explicit control of parallelism. MPI is portable to both distributed and shared memory architecture. The explicit parallelism often provides a better performance and a number of optimized collective communication routines are available for optimal efficiency.
MPI defines a high-level abstraction for fast and portable inter-process communication (Snir et al., 1998; Gropp et al., 1998). MPI applications can run in clusters of (possibly heterogeneous) workstations or dedicated nodes, (symmetric) multi-processors machines, or even a mixture of both. MPI hides all the low-level details, like networking or shared memory management, simplifying development and maintaining portability, without sacrificing performance.
The MPI specifications is nowadays the leading standard for message passing libraries in the world of parallel computers. At the time of this writing, clarifications to MPI-2 are being actively discussed and new working groups are being established for generating a future MPI-3 specification.
MPI provides the following functionality:
- Communication Domains and Process Groups: MPI communication operations occurs within a specific communication domain through an abstraction called communicator. Communicators are built from groups of participating processes and provide a communication context for the members of those groups. Process groups enable parallel applications to assign processing resources in sets of cooperating processes in order to perform independent work.
- Point-to-Point Communication: This fundamental mechanism enables the transmission of data between a pair of processes, one side sending, the other receiving.
- Collective Communications: They allow the transmission of data between multiple processes of a group simultaneously.
- Dynamic Process Management: MPI provides mechanisms to create or connect a set of processes and establish communication between them and the existing MPI application.
- One-Sided Operations: One-sided communications supplements the traditional two-sided, cooperative send/receive MPI communication model with a one-sided, remote put/get operation of specified regions of processes memory that have been made available for read and write operations.
- Parallel Input/Output.
B. OpenMP
OpenMP, the Open specifications for Multi-Processing (OpenMP, 2010), defines an application program interface that supports concurrent programming employing a shared memory model. OpenMP is available for several platforms and languages. There are extensions for most known languages like Fortran (77, 90 and 95) and C/C++. OpenMP is the result of the joint work between companies and educational institutions involved in the research and development of hardware and software.
OpenMP is based on the fork-join model (see Fig. 1), a paradigm implemented early on UNIX systems, where a task is divided into several processes (fork) with less weight than the initial task, and then collecting their results at the end and merging into a single result (join). Using OpenMP in existing codes implies the insertion of special compiler directives (beginning with #pragma omp in C/C++) and runtime routine calls. Additionally, environment variables can be defined in order to control some functionality at execution time.
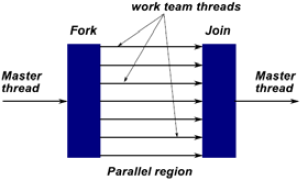
Figure 1: The master thread creates a team of parallel threads.
A code parallelized using OpenMP directives initially runs as a single process by the master thread or main process. Upon entering into a region to be parallalized the main process creates a set of parallel processes or parallel threads. Including an OpenMP directive implies a mandatory synchronization across the parallel block. That is, the code block is marked as parallel and threads are launched according to the characteristics of the directive. At the end of the parallel block, working threads are synchronized (unless an additional directive is inserted to remove this implicit synchronization). By default, in the parallelized region, all variables except those used in loops are shared by each thread. This can be changed by specifying the variable type (private or shared) before get into the parallel region. This model is also applicable to nested parallelism.
C. PETSc
PETSc (Balay et al., 2010a,b), the Portable Extensible Toolkit for Scientific Computation (PETSc), is a suite of data structures and routines for the scalable (parallel) solution of scientific applications modeled by partial differential equations. It employs the MPI standard for all message-passing communication. Being written in C and based on MPI, PETSc is a highly portable software library. PETScbased applications can run in almost all modern parallel environment, ranging from distributed memory architectures (Balay et al., 1997) (with standard networks as well as specialized communication hardware) to multi-processor (and multi-core) shared memory machines. PETSc library provides to its users a platform to develop applications exploiting fully parallelism and the flexibility to experiment many different models, linear and nonlinear large system solving methods avoiding explicit calls to MPI library. It is a freely available library usable from C/C++, Fortran 77/90 and Python (Dalcin, 2010). An overview of some of the components of PETSc can be seen in Fig. 2. An important feature of the package is the possibility to write applications at a high level and work the way down in level of abstraction (including explicit calls to MPI). As PETSc employs the distributed memory model, each process has its own address space. Data is communicated using MPI when required. For instance, in a linear (or nonlinear) system solution stage (a common case in FEM applications) each process will own a contiguous subset of rows of the system matrix (in the C implementation) and will primarily work on this subset, sending (or receiving) information to (or from) other processes. PETSc interface allows users an agile development of parallel applications. PETSc provides sequential/ distributed matrix and vector data structures, efficient parallel matrix/vector assembly operations using an object oriented style. Also, several iterative methods for linear/nonlinear solvers are designed in the same way.

Figure 2: Hierarchical structure of the PETSc library (taken from PETSc Manual (Balay et al., 2010a)).
III THE FastMat MATRIX CLASS
A. Preliminaries
Finite element codes usually have two levels of programming. In the outer level a large vector describes the "state" of the physical system. Usually the size of this vector is the number of nodes times the number of fields minus the number of constraints (e.g. Dirichlet boundary conditions). So that the state vector size is Nnod ndof-nconstr. This vector can be computed at once by assembling the right hand side (RHS) and the stiffness matrix in a linear problem, iterated in a non-linear problem or updated at each time step through solution of a linear or non-linear system. The point is that at this outer level all global assemble operations, that build the residual vector and matrices, are performed. At the inner level, one performs a loop over all the elements in the mesh, compute the RHS vector and matrix contributions of each element and assemble them in the global vector/matrix. From one application to another, the strategy at the outer level (linear/non-linear, steady/temporal dependent, etc) and the physics of the problem that defines the FEM matrices and vectors may vary.
The FastMat matrix class has been designed in order to perform matrix computations efficiently at the element level. One of the key points in the design of the matrix library is the characteristic of being thread-safe so that it can be used in an SMP environment within OpenMP parallel blocks. In view of efficiency there is an operation caching mechanism which will be described later. Caching is also thread-safe provided that independent cache contexts are used in each thread.
It is assumed that the code has an outer loop (usually the loop over elements) that is executed many times, and at each execution of the loop a series of operations are performed with a rather reduced set of local (or element) vectors and matrices.
In many cases, FEM-like algorithms need to operate on sub-matrices i.e., columns, rows or sets of them. In general, performance is degraded for such operations because there is a certain amount of work needed to extract or set the sub-matrix. Otherwise, a copy of the row or column in an intermediate object can be made, but some overhead is expected due to the copy operations.
The particularity of FastMat is that at the first execution of the loop the address of the elements used in the operation are cached in an internal object, so that in the second and subsequent executions of the loop the addresses are retrieved from the cache. The library is of public domain and can be accessed from (Storti et al., 2010).
A.1 Example
Consider the following simple example: A given 2D finite element mesh composed by triangles, i.e. an array xnod of 2×Nnod doubles with the node coordinates and an array icone with 3×nelem elements with node connectivities. For each element 0=j< nelem its nodes are stored at icone[3*j+k] for 0=k<2. For instance, it is required to compute the maximum and minimum value of the area of the triangles. This is a computation which is quite similar to those found in FEM analysis. For each element in the mesh two basic operations are needed: i) loading the node coordinates in local vectors x1, x2 and x3, ii) computing the vectors along the sides of the elements a=x2-x1 and b=x3-x1. The area of the element is, then, the determinant of the 2×2 matrix J formed by putting a and b as rows.
The FastMat code for the proposed computations is shown in Listing 1.

Listing 1: Simple FEM-like code
Calls to the FastMat::CacheCtx ctx object are related to the caching manipulation and will be discussed later. Matrices are dimensioned in line 3, the first argument is the matrix (rank), and then, follow the dimensions for each index rank or shape. For instance FastMat x(2,3,2) defines a matrix of rank 2 and shape (3,2), i.e., with 2 indices ranging from 1 to 3, and 1 to 2 respectively. The rows of this matrix will store the coordinates of the local nodes to the element. FastMat matrices may have any number of indices or rank. Also they can have zero rank, which stands for scalars.
A.2 Current matrix views (the so-called 'masks')
In lines 7 to 10 of code Listing 1 the coordinates of the nodes are loaded in matrix x. The underlying philosophy in FastMat is that "views" (or "masks") of the matrix can be made without making any copies of the underlying values. For instance the operation x.ir(1,k) (for "index restriction") sets a view of x so that index 1 is restricted to take the value k reducing in one the rank of the matrix. As x has two indices, the operation x.ir(1,k) gives a matrix of dimension one consisting in the k-th row of x. A call without arguments like in x.ir(.) cancels the restriction. Also, the function rs(.) (for "reset") cancels the actual view. Please, refer to the Appendix A for a synopsis of methods/operations available in the FastMat class.
A.3 Set operations
The operation a.set(x.ir(1,2)) copies the contents of the argument x.ir(1,2) in a. Also, x.set(xp) can be used, being xp an array of doubles (double *xp).
A.4 Dimension matching
The x.set(y) operation, where y is another FastMat object, requires that x and y have the same "masked" dimensions. As the .ir(1,2) operation restricts index to the value of 2, x.ir(1,2) is seen as a row vector of size 2 and then can be copied to a. If the "masked" dimensions do not fit then an error is issued.
A.5 Automatic dimensioning
In the example, a has been dimensioned at line 3, but most operations perform the dimensioning if the matrix has not been already dimensioned. For instance, if at line 3 a FastMat a is declared without specifying dimensions, then at line 12, the matrix is dimensioned taking the dimensions from the argument. The same applies to set(Matrix &) but not to set(double *) since in this last case the argument (double *) does not give information about his dimensions. Other operations that define dimensions are products and contraction operations.
A.6 Concatenation of operations
Many operations return a reference to the matrix (return value FastMat &) so that operations may be concatenated as in A.ir(1,k).ir(2,j).
A.7 Underlying implementation with BLAS/LAPACK
Some functions are implemented at the low level using BLAS(BLAS, 2010)/LAPACK(Lapack, 2010). Notably prod() uses BLAS's dgemm so that the amortized cost of the prod() call is the same as for dgemm(). As a matter of fact, a profiling study of FastMat efficiency in a typical FEM code has determined that the largest CPU consumption in the residual/Jacobian computation stage corresponds to prod() calls. Another notable case is eig() that uses LAPACK dgeev. The eig() method is not commonly used, but if it does, its cost may be significant so that a fast implementation as proposed here with dgeev is mandatory.
A.8 The FastMat operation cache concept
The idea with caches is that they are objects (class FastMatCache) that store the addresses and any other information that can be computed in advance for the current operation. In the first pass through the body of the loop (i.e., ie=0 in the example of Listing 1) a cache object is created for each of the operations, and stored in a list. This list is basically a doubly linked list (list< >) of cache objects. When the body of the loop is executed the second time (i.e., ie>1 in the example) and the following, the addresses of the matrix elements are not needed to be recomputed but they are read from the cache instead. The use of the cache is rather automatic and requires little intervention by the user but in some cases the position in the cache-list can get out of synchronization with respect to the execution of the operations and severe errors may occur.
The basic use of caching is to create the cache structure FastMat::CacheCtx ctx and keep the position in the cache structure synchronized with the position of the code. The process is very simple, when the code consists in a linear sequence of FastMat operations that are executed always in the same order. In this case the CacheCtx object stores a list of the cache objects (one for each Fast-Mat operation). As the operations are executed the internal FastMat code is in charge of advancing the cache position in the cache list automatically. A linear sequence of cache operations that are executed always in the same order is called a branch.
Looking at the previous code, it has one branch starting at the x.ir(1,k).set(...) line, through the J.rs().det() line. This sequence is repeated many times (one for each element) so that it is interesting to reuse the cache list. For this, a branch object b1 (class FastMat:: Cache Ctx::Branch) and a jump to this branch are created each time a loop is executed. In the first loop iteration the cache list is created and stored in the first position of the cache structure. In the next and subsequent executions of the loop, the cache is reused avoiding recomputing many administrative work related with the matrices.
The problem is when the sequence of operations is not always the same. In that case several jump() commands must be issued, each one to the start of a sequence of Fast-Mat operations. Consider for instance the following code,

A vector x of size 3 is randomly generated in a loop (the line x.fun(rnd);). Then its length is computed, and if it is shorter than 1.0 it is scaled by 1.0/len, so that its final length is one. In this case two branches are defined and two jumps are executed,
branch b1: operations x.fun() and x.norm_p_all(),
branch b2: operation x.scale().
B. Caching the addresses used in the operations
If caching is not used the performance of the library is poor while the cached version is very fast, in the sense that almost all the CPU time is spent in performing multiplications and additions, and negligible CPU time is spent in auxiliary operations.
B.1 Branching is not always needed
However, branching is needed only if the instruction sequence changes during the same execution of the code. For instance, if a code like follows is considered

the method flag is determined at the moment of reading the data and then is left unchanged for the whole execution of the code, then it is not necessary to "jump()" since the instruction sequence will be always the same.
B.2 Cache mismatch
The cache process may fail if a cache mismatch is produced. For instance, consider the following variation of the previous code

There is an additional block in the conditional, if the length of the vector is greater than 1.1, then the vector is set to the null vector.
Every time that a branch is opened in a program block a ctx.jump() must be called using different arguments for the branches (i.e., b1, b2, etc). In the previous code there are three branches. The code shown is correct, but assume that the user forgets the jump() calls at lines 10 and 13 (sentences ctx.jump(b2) and ctx.jump (b3)), then when reaching the x.set(0.0), the operation in line 14, the corresponding cache would be the cache corresponding to the x.scale() operation (line 11), and an incorrect computation will occur.
Each time that the retrieved cache does not match with the operation that will be computed or even when it does not exist a cache mismatch exception is produced.
B.3 Causes for a cache mismatch error
Basically, the information stored in the cache (and then, retrieved from the objects that were passed in the moment of creating the cache) must be the same needed for performing the current FastMat operation, that is
- The FastMat matrices involved must be the same, (i.e. their pointers to the matrices must be the same).
- The indices passed in the operation must coincide (for instance for the prod(), ctr, sum() operations).
- The masks (see III.A.2) applied to each of the matrix arguments must be the same.
B.4 Multi-threading and reentrancy
If caching is not enabled, FastMat is thread safe. If caching is enabled, then it is thread safe in the following sense, a context ctx must be created for each thread, and the matrices used in each thread must be associated with the context of that thread.
If creating the cache structures each time is too bad for efficiency, then the context and the matrices may be used in a parallel region, stored in variables, and reused in a subsequent parallel region.
C. Efficiency
This benchmark computes a=b*c in a loop for a large number N of distinct square matrices a, b, c of varying size n. As mentioned before the amortized cost is the same as the underlying dgemm() call. The processing rate in Gflops is computed on the base of an operation count per matrix product, i.e. 2n3
 | (1) |
The number of times for reaching a 50% amortization (n1/2) is in the order of 15 to 30. With respect to the dgemm() implementation for the matrix product, several options were tested on an Intel Core 2 Duo T5450 (1.66GHz) processor using one core (see Fig. 3). The options tested were: i) the Atlas (Whaley et al., 2001) self-configurable version, both with the default setup and self-configured; ii) the Intel Math Kernel Library (MKL) library, with the GNU/GCC g++ and iii) Intel icc compilers. A significant improvement is obtained if the library is linked to the MKL, combined with either icc or g++ compiler. This combinations peak at 5 to 6 Gflops for 100< n<200. With operation caching activated the overhead of the mask computation is avoided, and the amortized cost is similar to using dgemm() on plain C matrices.
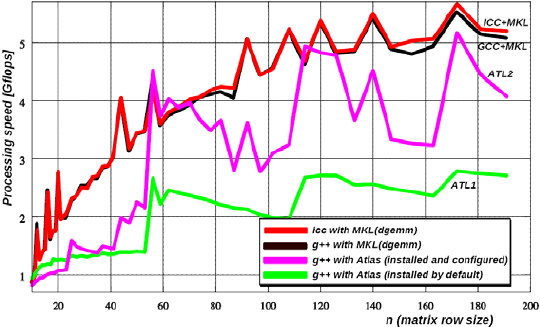
Figure 3: Efficiency comparatives on Intel Core 2 Duo T5450 (1.66GHz) processor
D. FastMat "Multi-product" operation
A common operation in FEM codes (see Section V) and many other applications is the product of several matrices or tensors. In addition, this kind of operation usually consume the largest part of the CPU time in a typical FEM computation of residuals and Jacobians. The number of operations (and consequently the CPU time) can be largely reduced by choosing the order in which the products are performed.
For instance consider the following operation
 | (2) |
(Einstein's convention on repeated indices is assumed). The same operation using matricial notation is
| A = BCD | (3) |
where A, B, C, D are rectangular (rank 2) matrices of shape (m1,m4), (m1,m2), (m2,m3), (m3,m4), respectively. As the matrix product is associative the order in which the computations are performed can be chosen at will, so that it can be performed in the following two ways
 | (4) |
The order in which the computations are performed can be represented by a Complete Binary Tree. In this paper the order will be described using parentheses. The number of operations (op. count) for the different trees, and in consequence the CPU time, can be very different. The cost of performing the first product BC in the first row of (4) (and a product of two rectangular matrices in general) is
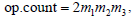 | (5) |
which can be put as,
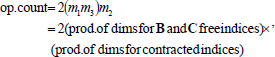 | (6) |
or alternatively,
 | (7) |
and for the second product is 2m1m3m4 so that the total cost for the first computation tree CT1 is 2m1m3(m2+ m4). If the second computation tree CT2 is used, then the number of operations is 2m2m4(m1+ m3). This numbers may be very different, for instance when B and C are square matrices and D is a vector, i.e. m1=m2=m3= m> 1, m4 =1. In this case the operation count is 2m2(m+ 1) = O(m3) for CT1 and 4m2= O(m2) for CT2, so that CT2 is much more convenient.
D.1. Algorithms for the determination of the computation tree
There is a simple algorithm that exploits this heuristic rule in a general case (Aho et al., 1983). If the multi-product is
| R = A1 A2 ... An , | (8) |
with Ak of shape (mkmk+1), then the operation count ck for each of the possible products AkAk+1, is computed, namely ck= mkmk+1m k+2 for k =1 to n-1. Let cflk* be the minimum operation count, then the corresponding product Ak*Ak*+1 is performed and the pair Aq, Aq+1 is replaced by this product. Then, the list of matrices in the multi-product is shortened by one. The algorithm proceeds recursively until the number of matrices is reduced to only one. The cost of this algorithm is O(n2) (please note that this refers to the number of operations needed to determine the computation tree, not in actually computing the matrix product).
For a small number of matrices the optimal tree may be found by performing an exhaustive search over all possible orders. The cost is in this case O(n!). In Fig. 4 the computing times of the exhaustive optimal and the heuristic algorithms is shown for a number of matrices up to 8. Of course it is prohibitive for a large number of matrices, but it can be afforded for up to 6 or 7 matrices, which is by far the most common case. The situation is basically the same but more complex in the full tensorial case, as it is implemented in the FastMat library. First consider a product of two tensors like this
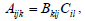 | (9) |

Figure 4: Cost of determination of the optimal order for computing the product of matrices with the heuristic and exhaustive (optimal) algorithms.
where tensors A, B, C have shape (m1,m2,m3), (m3,m4,m2), (m1,m4) respectively. i, j, k are free indices while l is a contracted index. The cost of this product is (Eqs. 6 and 7)
 | (10) |
On one hand, the modification with respect to the case of rectangular (rank 2) matrices is that every matrix can be contracted with any other in the list. So that, the heuristic algorithm must check now all the pair of distinct matrices which is n'(n'- 1)/2 where 1=n'< n is the number of actual matrices. This must be added over n' so that the algorithm is O(n3). On the other hand, regarding the optimal order, it turns out to be that the complexity for its computation is
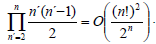 | (11) |
In the FastMat library the strategy is to use the exhaustive approach for n=nmax and the heuristic one. Otherwise, with nmax=5 by default but dynamically configurable by the user.
D.2. Example: Computation of SUPG stabilizatiofln term. Element residual and Jacobian
As an example, consider the computation of the stabilization term (see Section V) for general advective-diffusive systems. The following product must be computed
 | (12) |
where
 (shape (nel,ndof), identifier res) is the SUPG residual contribution from the element e (see Section V and Eq. 15),
(shape (nel,ndof), identifier res) is the SUPG residual contribution from the element e (see Section V and Eq. 15),- ?p,flk (shape (ndim,nel), identifier gN) are the spatial gradients of the interpolation functions ?p,
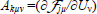 (shape (nel,ndof,ndof), identifier A) are the Jacobians of the advective fluxes
(shape (nel,ndof,ndof), identifier A) are the Jacobians of the advective fluxes 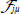 with respect to the state variables U?,
with respect to the state variables U?,- t?a (shape (ndof, ndof ), identifier tau) is the matrix of intrinsic times, and
 (shape (ndof), identifier R) is the vector of residuals per field at the Gauss point.
(shape (ndof), identifier R) is the vector of residuals per field at the Gauss point.
This tensor products arise, for instance, in the context of the FEM-Galerkin SUPG stabilizing methods (see References Donea and Huerta., 2003; Tezduyar and Osawa, 2000). This multi-product is just an example of typical computations that are performed in a FEM based CFD code. This operation can be computed in a FastMat call like this
res.prod(gN,A,tau,R,-1,1,-1,2,-2,-2,-3,-3);
where if the j-th integer argument is positive it represents the position of the index in the resulting matrix, otherwise if the j-th argument is -1 then a contraction operation is performed over all these indices (see Appendix A.C).
The FastMat::prod() method then implements several possibilities for the computing tree
- natural: The products are performed in the order the user has entered them, i.e. (((A1A2)A3)A4)...
- heuristic: Uses the heuristic algorithm described in Section III.D.1.
- optimal: An exhaustive brute-force approach is applied in order to determine the computation tree with the lowest operation count.
In Table 1 the operation counts for these three strategies are reported. The first three columns show the relevant dimension parameters. ndim may be 1,2,3 and nel may be 2 (segments), 3 (triangles), 4 (quads in 2D, tetras in 3D) and 8 (hexahedra). The values explored for ndof are
ndof=1: scalar advection-diffusion,
ndof= ndim +2: compressible flow,
ndof= 10: advection-diffusion for 10 species.
Table 1: Operation count for the stabilization term in the SUPG formulation of advection-diffusion of ndof number of fields. Other relevant dimensions are the space dimension ndim and the number of nodes per element nel.

Operation counts for the computation of element residuals. The costs of the tensor operation defined in Eq. (12) (where the involved tensors are as described above) are evaluated in terms of the gains (%) (see Table 1). The gains are related to the cost of products performed in the natural order, so that
- CT1 is: ((gN*R)*tau)*A
- CT2 is: (gN*(tau*R))*A
- CT3 is: gN*((A*tau)*R)
- CT4 is: gN*(A*(tau*R))
Operation counts for the computation of element Jacobians. This product is similar as the one described above, but now the Jacobian of the residual term is computed so that the last tensor is not a vector, but rather a rank 3 tensor.
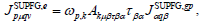 | (13) |
J.prod(gN,A,tau,JR,-1,1,-1,2,-2, -2,-3,-3,3,4);
where  (shape (ndof ,nel,ndof), identifier JR) is the Jacobian of residuals per field at the Gauss point.
(shape (ndof ,nel,ndof), identifier JR) is the Jacobian of residuals per field at the Gauss point.
Possible orders (or computation trees):
- CT5: ((gN*A)*tau)*JR
- CT6: (gN*(A*tau))*JR
- CT7: gN*((A*tau)*JR)
Discussion of the influence of computation tree From the previous examples it is noticed that:
In many cases the use of the CT determined with the heuristic or optimal orders yields a significant gain in operation count. The gain may be 90% or even higher in a realistic case like the computations for Eqs. (12) and (13).
- In the presented cases, the heuristic algorithm yielded always a reduction in operation count, though in general this is not guaranteed. In some cases the heuristic approach yielded the optimal CT. In others it gave a gain, but far from the optimal one.
- It is very interesting that neither the heuristic nor optimal computation trees are the same for all combinations of parameters (ndim,nel,ndof). For instance in the computation of the Jacobian the optimal order is (gN*(A*tau))*JR in some cases and gN*((A*tau)*JR) in others (designated as CT6 and CT7 in the tables). This means that it would be impossible for the user to choose an optimal order for all cases. This must be computed automatically at run-time as proposed here in FastMat library.
- In same cases the optimal or heuristically determined orders involve contractions that are not in the natural order, for instance the CT (gN*(tau*R))*A (designated as CT2) is obtained with the heuristic algorithm for the computation of the element residual for some set of parameters. Note that the second scheduled contraction involves the gN and tau*R tensors, even if they do not share any contracted indices.
Note that, in order to perform the computation of an efficient CT for the multi-product (with either the heuristic or optimal algorithms) it is needed that the library implements the operation in functional form as in the FastMat library. Operator overloading is not friendly with the implementation of an algorithm like this, because there is no way to capture the whole set of matrices and the contraction indices. The computation of the optimal or heuristic order is done only once and stored in the cache. In fact this is a very good example of the utility of using caches.
Using more elaborated estimations of computing time. In the present work it is assumed that the computing time is directly proportional to the number of operations. This may not be true, but note that the computation tree could be determined with a more direct approach. For instance, by benchmarking the products and then determining the CT that results in the lowest computing time, not in operation count.
IV COMBINING MPI WITH OPENMP
To exploit the benefits of both parallel approaches the so-called hybrid programming paradigm was used earlier when multi-core processors become available and Massively Parallel Processing (MPP) systems were abandoned in favor of clusters of SMP nodes. In the hybrid model, each SMP node executes one multi-threaded MPI process (here this is done by implementing OpenMP directives) while in pure MPI programming, each processor executes a single-threaded MPI process.
The hybrid model approach not always provides many benefits. For example, (Henty, 2000) observed that although in some cases OpenMP was more efficient than MPI on a single SMP node (flat MPI), hybrid parallelism did not outperform pure message-passing on an SMP cluster. Also, according to Smith and Bull (2001), this style of programming cannot be regarded as the ideal programming model for all codes. Nevertheless, a significant benefit may be obtained if the parallel MPI code suffers from poor scaling due to load imbalance or too fine grained tasks.
On one hand, if the code scales poorly with an increasing number of SMP nodes and a multi-threading implementation of a specific part of it scales well, it may be expected an improvement in performance on a mixed code. This is because intra-node communication disappears. On the other hand, if an MPI code scales poorly due to load imbalance an hybrid programming code version will create a coarser grained problem. Thus improving the code performance inasmuch as MPI will only be used for communication between nodes.
Table 2: Operation count for the Jacobian of the SUPG term in the for ndof number of fields. Other relevant dimensions are the space dimension ndim and the number of nodes per element nel.

Typically, a mixed mode code involves a hierarchical model where MPI parallelization occurs at top level (coarse grain) and multi-threading parallelization below (fine grain). This implies that MPI routines are called outside parallel regions while all threads but the master are sleeping. This approach provides a portable parallelization and it is the scheme used in this work. Thread-safe objects, like FastMat ones, are also needed in this technique.
Hybrid MPI/OpenMP parallelization
In this work hybrid parallelism is evaluated with a C++ code for the solution of the scalar advection-diffusion partial differential equation by means of a stabilized finite element method. The parallel code was implemented using MPI, PETSc and OpenMP, having four main parts:
- Problem Partition across SMP nodes: each node stores a portion of the mesh elements and the associated degrees-of-freedom. Besides, a parallel matrix and work vectors are created (MatCreateMPIAIJ, VecCreateMPI).
- Element FEM matrices and RHS computation: each SMP node performs a loop over the owned partition of the elements in the mesh and computes element matrices and right hand side contributions using OpenMP threads. Each thread performs the computations of its assigned group of elements according to a selected OpenMP scheduling (static, dynamic, guided).
- Matrix/Vector Values Assembly: vector and matrix element contributions are stored in PETSc Matrices and Vectors objects (VecSetValue, MatSetValue) on each SMP node. After that, {Vec|Mat}Assembly Begin and {Vec|Mat}AssemblyEnd are called in order to communicate the off-process vector/matrix contributions and to prepare internal matrix data structures for subsequent operations like parallel matrix-vector product.
- Linear System Solving: a suitable iterative Krylov Space-based linear solver (KSP objects) is used. The matrix-vector product is a highly demanding operation of most iterative Krylov methods. The MatMult operation which is employed in all PETSc Krylov solvers is also parallelized using OpenMP threads inside an SMP node. For this purpose, OpenMP directives are introduced at the row loop of the sparse matrix-vector product.
V TEST CASE: ADVECTION-DIFFUSION SKEW TO THE MESH
The scalar advection-diffusion equation to be solved is,
 | (14) |
where u is the unknown scalar, a is the advection velocity vector, ?>0 is the diffusion coefficient and s(x) is a volumetric source term. For the sake of simplicity only Dirichlet and Neumann boundary conditions are considered. Prescribed values for Dirichlet and Neumann conditions are uD and q, and n is the unit exterior normal to the boundary G N.
The discrete variational formulation of (14) with added SUPG stabilizing term (Tezduyar and Osawa, 2000) is written as follows: find uh?Sh such that
 | (15) |
where
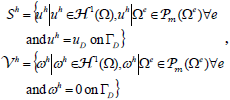 | (16) |
where  is the finite element interpolating space. According to Tezduyar and Osawa (2000) the stabilization parameter tsupg is computed as
is the finite element interpolating space. According to Tezduyar and Osawa (2000) the stabilization parameter tsupg is computed as
 | (17) |
with
 | (18) |
where s is a unit vector pointing in the streamline direction.
The problem statement is depicted in Fig. 5 where the computational domain is a unit square, i.e., ?= (x,y) in [0, 1]× [0, 1]. This 2D test case has been widely used to illustrate the effectiveness of stabilized finite element methods in the modeling of advection-dominated flows (Donea and Huerta., 2003). The flow is unidirectional and constant,  , but the advection velocity is skew to the mesh with an angle of 30°. The diffusion coefficient is 10-4, thus obtaining an advection-dominated system. As shown in Fig. 5, Dirichlet boundary conditions are imposed at inlet walls (x=0 and y=0 planes) while at outlet walls (x=1 and y=1 planes) Neumann homogeneous conditions are considered.
, but the advection velocity is skew to the mesh with an angle of 30°. The diffusion coefficient is 10-4, thus obtaining an advection-dominated system. As shown in Fig. 5, Dirichlet boundary conditions are imposed at inlet walls (x=0 and y=0 planes) while at outlet walls (x=1 and y=1 planes) Neumann homogeneous conditions are considered.

Figure 5: Advection of discontinuous inlet data skew to the mesh: problem statement.
A solution obtained on a coarse mesh is plotted in Fig. 6.

Figure 6: SUPG solution for the 2D convection-diffusion problem with downwind natural conditions in a coarse mesh.
A. Results
The equipment used to perform the tests was the Coyote cluster at CIMEC laboratory. This is a Beowulf-class cluster, consisting of a server and 6 nodes dual quad-core Intel Xeon E5420 (1333Mhz Front Side Bus, FSB) 2.5 GHz CPU with 8 Gb RAM per node (see Fig. 11.a), interconnected via a Gigabit Ethernet network.

Figure 11: dual Xeon and i7 archs.
In order to compute the performance of the proposed algorithm a mesh of 4.5 millions of linear triangles (with linear refinement toward walls) is used. As the system of linear equations arising from (15) is non-symmetric, the Stabilized Bi-Conjugate Gradient (BiCG-Stab) method with diagonal preconditioning is employed as solver (Saad., 2000).
The results for the consumed wall-clock time while sweeping the number of SMP nodes (np) and the number of threads (nc) are shown in Fig. 7 for the RHS and matrix computation; and in Fig. 8 for the MatMult operation.
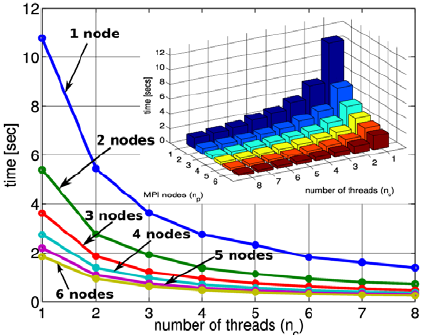
Figure 7: Elapsed time for the RHS and matrix computation.

Figure 8: Elapsed time for the MatMult solver operation.
Let T* be the execution time to solve the problem on 1 node and 1 thread (np=1 and nc=1) and T denote the execution time of the parallel algorithm when there are np MPI processes each running nc OpenMP threads. Then, the speedup S and efficiency E are defined as
 | (19) |
 | (20) |
respectively. The speedup obtained for the RHS and matrix computation are illustrated in Fig. 9 and for the MatMult operation in Fig. 10.

Figure 9: Speedup for the RHS and matrix computation.

Figure 10: Speedup for the MatMult iterative solver operation.
As shown through Figs. 7 to 9, the Matrix and RHS computation stage scales linearly for the whole range of SMP nodes and numbers of considered cores/threads as expected. This stage is highly parallelizable (i.e., do not require inter-node communications) and the performance is only slightly degraded. The memory access pattern of this stage consists on loading a few element data from memory (like nodal coordinates and a few physical parameters) and computing several quantities with them (element area, interpolation functions, gradients, element contribution to global FEM matrix, etc). Thus, the ratio between floating point operations and memory accesses is high. As expected, this stage is not appreciably influenced by memory bandwidth.
On one hand, when considering the left plot of Fig. 9, it can be seen from the blue line labeled ("1 thread") that pure MPI run scaling is linear. On the other hand, if axis line np=1 is considered (or the blue line labeled "1 node" in the right plot of the same figure), OpenMP threaded runs also show linearity. Beyond what has been said, all hybrid runs exhibit the same behavior with a maximum loss in efficiency of about 10% (for the case of np =6 and nc =8 threads).
The situation is clearly different for the MatMult operation (Figs. 8 and 10). In this case, although pure MPI/PETSc runs represented by the blue line labeled "1 thread" in the left part of Fig. 10 show a linear scaling when varying the number of SMP processors (or nodes), the hybrid runs show an appreciable degradation of speedup. A speedup of 10 is obtained for 6 nodes with 8 cores, whereas the theoretical value is 48. This loss in efficiency can be better appreciated on the right plot of the Figure where speedup stagnates beyond four threads. In sparse matrix-vector product, the ratio between floating point operations and memory accesses is low. Thus, the overall performance in this stage is mainly controlled by memory bandwidth.
B. OpenMP and Flat MPI on one multi-processor machine
A speedup comparison between pure OpenMP and pure MPI versions of the FEM code running on one multiprocessor machine was made using a mesh of 2 millions of linear triangles. Two different architectures are used separately: a quad-core Intel i7-950 (3.07Ghz) machine and a dual Intel quad-core (dual-die dual-core each processor) Xeon E5420 (2.5GHz) with a 1333Mhz Front Side Bus (FSB).
Common features of all Nehalem (and so that the i7 processor) based processors include an integrated DDR3 memory controller as well as QuickPath Interconnect (QPI) on the processor replacing the Front Side Bus used in earlier Core processors like the Xeon architecture. Besides, Nehalem processors have 256KB on-die L2 cache per core, plus up to 12 MB shared on-die L3 cache. QPI is much faster than FSB and hence improves the overall performance. The Core i7 have an on-die memory controller which means that it can access memory much faster than the dual core Xeon processors (that have an external memory controller), therefore improving the overall performance.
The hierarchical topology, including memory nodes, sockets, shared caches and cores of the processors involved in this test are sketched in Fig. 11. They were obtained using hwloc (hwloc, 2010). Figures 12 and 13 show the speedups obtained on Xeon and i7 architectures, respectively, for the matrix and RHS computation and for the iterative system solution stages (MatMult). Performances when computing the FEM matrix and the RHS are comparable with those presented in the previous tests. Regarding the linear system solution stage, as shown in the right plot of Fig. 12 and 13, i7 processor performs slightly better than Xeon processor considering runs with varying number of threads (OpenMP) or processes (flat MPI) from one to four. Beyond that, when running the test using five to eight threads/ processes in the Xeon processor (recall that i7 processor has only 4 cores and Xeon has 8 cores), the memory bandwidth saturates and there is no improvement of performance in the MatMult operation.
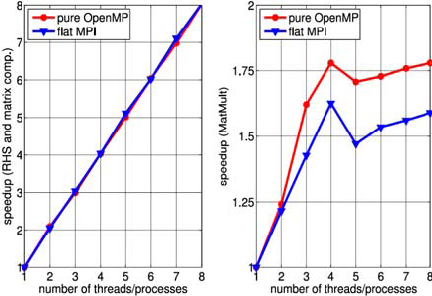
Figure 12: Speedup for the RHS and matrix computations (left) and MatMult op. (right) stages in Xeon architecture.
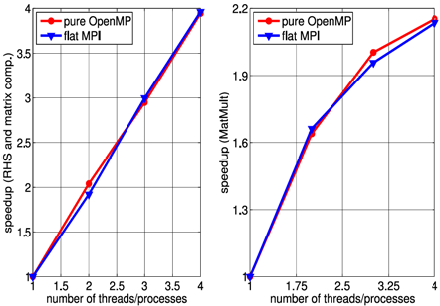
Figure 13: Speedup for the RHS and matrix computations (left) and MatMult op. (right) stages in i7 architecture.
VI CONCLUSIONS
The computation, assembly and solution stages in typical Finite Element codes have been discussed and studied in order to exploit the advantages provided by new hybrid architectures, like clusters of multi-core processors. For this purpose an efficient tensor library, which is thread-safe, is presented and rigorously evaluated. Having in mind that for large scale meshes all FEM computation inside the loop over elements must be evaluated millions of times, the process of caching all FEM operations at the element level (provides by FastMat library) is a key-point in the performance for the computing/assembling stages. The most important features of the FastMat tensor library can be summarized as follows:
- Highly repeated tensorial operations at the element level are cached. Hence, element routines are very fast, in the sense that almost all the CPU time is spent in performing multiplications and additions, and negligible CPU time is spent in auxiliary operations. This feature is the key-point when dealing with large/fine FEM meshes.
- For the very common multi-product tensor operation, the order in which the successive tensor contractions are computed is always performed at the minimum operation count cost depending on the number of tensor/matrices in the FEM terms (exhaustive or heuristic approaches).
- The FastMat library is fully tensorial in the sense that contractions are implemented in a general way. The number of contracted tensors and the range of their indices can be variable. Also, a complete set of classical tensorial functions are available in the library.
- The FastMat library is "thread-safe", i.e., element residuals and Jacobians can be computed in the context of multi-threaded FEM codes.
Also, in this article, a stabilized finite element formulation of the linear scalar advection-diffusion equation has been implemented. This formulation is used to analyze the performance of computing the element contributions and the assemble process using the FastMat library and the multi-threaded version of PETSc's linear equation solver on a cluster of SMP nodes (hybrid architecture).
Extending pure MPI FEM codes to be used on hybrid clusters with OpenMP is not a difficult task. It could be only based on the different levels of parallelism of each part of the code. Implementing MPI/OpenMP hybrid codes starting from threaded codes generally requires much effort, especially when considering the linear and non-linear solution stages.
FEM code developers and researchers can take advantages from spreading hybrid architectures combining MPI and OpenMP standards. Nonetheless, as it was shown in tests, it seems that there is a limitation on the performance of architectures implementing the FSB model, which is not appreciably improved on i7 architectures. Thus, numerical algorithms with low ratios between floating point operations and memory accesses would perform poorly on hybrid environments.
APPENDIX A: SYNOPSIS OF FASTMAT OPERATIONS
A. One-to-one operations
The operations are from one element of A to the corresponding element in *this.
The one-to-one operations implemented so far are
- FastMat& set(const FastMat &A): Copy matrix.
- FastMat& add(const FastMat &A): Add matrix.
- FastMat& rest(const FastMat &A): Substract a matrix.
- FastMat& mult(const FastMat &A): Multiply (element by element) (like Matlab .*).
- FastMat& div(const FastMat &A): Divide matrix (element by element, like Matlab ./).
- FastMat& axpy(const FastMat &A, const double alpha): Axpy operation (element by element): (*this) += alpha * A
B. In-place operations
These operations perform an action on all the elements of a matrix.
- FastMat& set(const double val=0.): Sets all the element of a matrix to a constant value.
- FastMat& scale(const double val): Scale by a constant value.
- FastMat& add(const double val): Adds constant val.
- FastMat& fun(double (*)(double) *f): Apply a function to all elements.
C. Generic "sum" operations (sum over indices)
These methods perform some associative reduction operation an all the indices of a given dimension resulting in a matrix which has a lower rank. It's a generalization of the sum/max/min operations in Matlab that returns the specified operation per columns, resulting in a row vector result (one element per column). Here you specify a number of integer arguments, in such a way that
- if the j-th integer argument is positive it represents the position of the index in the resulting matrix, otherwise
- if the j-th argument is -1 then the specified operation (sum/max/min etc...) is performed over all this index.
For instance, if a FastMat A(4,2,2,3,3) is declared then B.sum(A,-1,2,1,-1) means
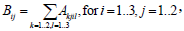 | (21) |
These operations can be extended to any binary associative operation. So far the following operations are implemented
- FastMat& sum(const FastMat &A, const int m=0,..): Sum over all selected indices.
- FastMat& sum_square(const FastMat &A, const int m=0,..): Sum of squares over all selected indices.
- sum_abs(const FastMat &A,+ const int m=0,..): Sum of absolute values all selected indices.
- FastMat& min(const FastMat &A, const int m=0,..): Minimum over all selected indices.
- FastMat& max(const FastMat &A, const int m=0,..): Maximum over all selected indices.
- FastMat& min_abs(const FastMat &A, const int m=0,..): Min of absolute value over all selected indices.
- FastMat& max_abs(const FastMat &A, const int m=0,..): Max of absolute value over all selected indices.
D. Sum operations over all indices
When the sum is over all indices the resulting matrix has zero dimensions, so that it is a scalar. You can get this scalar by creating an auxiliary matrix (with zero dimensions) casting with operator double() as in
FastMat A(2,3,3),Z;
... // assign elements to A
double a = double(Z.sum(A,-1,-1));
or using the get() function
double a = Z.sum(A,-1,-1).get();
without arguments, which returns a double. In addition there is for each of the previous mentioned "generic sum" function a companion function that sums over all indices. The name of this function is obtained by appending _all to the generic function
double a = A.sum_square_all();
The list of these functions is
- double sum_all() const: Sum over all indices.
- double sum_square_all() const: Sum of squares over all indices.
- double sum_abs_all() const: Sum of absolute values over all indices.
- double min_all() const: Minimum over all indices.
- double max_all() const: Maximum over all indices.
- double min_abs_all() const: Minimum absolute value over all indices.
- double max_abs_all() const: Maximum absolute value over all indices.
E. Export/Import operations
These routines allow to convert matrices from or to arrays of doubles
- FastMat& set(const double *a): Copy from array of doubles.
- FastMat& export(double *a): exports to a double vector.
ACKNOWLEDGMENTS
This work has received financial support from Consejo Nacional de Investigaciones Científlfiflcas y Técnicas (CONICET, Argentina, grant PIP 5271/05), Universidad Nacional del Litoral (UNL, Argentina, grants CAI+D 2009 65/334), Agencia Nacional de Promoción Científlfiflca y Tecnológica (ANPCyT, Argentina, grants PICT 01141/2007, PICT 2008-0270 "Jóvenes Investigadores", PICT-1506/2006) and Secretaría de Ciencia y Tecnología de la Universidad Tecnológica Nacional, Facultad Regional Resistencia (Chaco).
REFERENCES
1. Aho, A.V., J.D. Ullman and J.E. Hopcroft. Data structures and algorithms, Addison Wesley (1983). [ Links ]
2. Balay, S., W.D. Gropp, L. Curfman McInnes and B.F. Smith, Efficient management of parallelism in object oriented numerical software libraries, 163-202 (1997). [ Links ]
3. Balay, S., K. Buschelman, V. Eijkhout, W.D. Gropp, D. Kaushik, M.G. Knepley, L. Curfman McInnes, B.F. Smith and H. Zhang, PETSc users manual. technical report ANL-95/11 (2010a). [ Links ]
4. Balay, S., K. Buschelman, W.D. Gropp, D.Kaushik, M.G. Knepley, L.Curfman McInnes, B.F. Smith and H. Zhang. PETSc Web page. URL http://www.mcs.anl.gov/petsc (2010b). [ Links ]
5. Behara, S. and S. Mittal, "Parallel finite element computation of incompressible flows," Parallel Computing, 35, 195- 212 (2009). [ Links ]
6. BLAS, BLAS-Basic Linear Algebra Subprograms, URL http://www.netlib.org/blas (2010). [ Links ]
7. Dalcin, L.D., PETSc for Python, URL http://petsc4py.googlecode.com (2010). [ Links ]
8. Donea, J. and A. Huerta, Finite element methods for flow problems, Wiley and Sons (2003). [ Links ]
9. Gropp, W., S. Huss-Lederman, A. Lumsdaine, E. Lusk, B. Nitzberg, W. Saphir and M. Snir, The MPI-2 Extensions, volume 2 of MPI -The Complete Reference. MIT Press, Cambridge, 2 edition (1998). [ Links ]
10. Henty, D.S., "Performance of hybrid message-passing and shared-memory parallelism for discrete element modeling," Proceedings of Supercomputing 00 (2000). [ Links ]
11. Hwloc, Portable hardware locality (hwloc), URL http://www.open-mpi.org/projects/hwloc (2010). [ Links ]
12. Jost, G. and H. Jin, "Comparing the OpenMP, MPI, and hybrid programming paradigms on an SMP cluster," Fifth European Workshop on OpenMP (2003). [ Links ]
13. Lapack, LAPACK -Linear Algebra PACKage, URL http://www.netlib.org/lapack (2010). [ Links ]
14. MPI, MPI Web page, URL http://www.mpi-forum.org (2010). [ Links ]
15. OpenMP, OpenMP specification, URL http:// openmp. org/wp/ openmp-specifications (2010). [ Links ]
16. Paz, R.R., N.M. Nigro and M.A.Storti, "On the efficiency and quality of numerical solutions in CFD problems using the interface strip preconditioner for domain decomposition methods," International Journal for Numerical Methods in Fluids, 51, 89-118 (2006). [ Links ]
17. Saad, Y., Iterative Methods for Sparse Linear Systems. PWS Publishing Co. (2000). [ Links ]
18. Smith, L. and M. Bull, "Development of mixed mode MPI/OpenMP applications," Scientific Programming, 9, 83-98 (2001). [ Links ]
19. Snir, M., S. Otto, S. Huss-Lederman, D. Walker and J. Dongarra, The MPI Core, volume 1 of MPI -The Complete Reference. MIT Press, Cambridge, 2 edition (1998). [ Links ]
20. Sonzogni, V., A. Yommi, N.M. Nigro and M.A. Storti, "A parallel finite element program on a Beowulf cluster," Advances in Engineering Software, 33, 427-443 (2002). [ Links ]
21. Storti, M.A., N.M. Nigro, R.R. Paz and L.D. Dalcin, PETSc-FEM: A General Purpose, Parallel, Multi-Physics FEM Program, URL http://www.cimec.org.ar/petscfem (2010). [ Links ]
22. Tezduyar, T. and Y. Osawa, "Finite element stabilization parameters computed from element matrices and vectors," Computer Methods in Applied Mechanics and Engineering, 190, 411-430 (2000). [ Links ]
23. Whaley, R.C., A. Petitet and J. Dongarra, "Practical experience in the numerical dangers of heterogeneous computing," Parallel Computing, 27, 3-35 (2001). [ Links ]
Received: September 19, 2010
Accepted: October 21, 2010
Recommended by subject editor: Eduardo Dvorkin













