Servicios Personalizados
Revista
Articulo
Indicadores
-
 Citado por SciELO
Citado por SciELO
Links relacionados
-
 Similares en
SciELO
Similares en
SciELO
Compartir
Latin American applied research
versión impresa ISSN 0327-0793
Lat. Am. appl. res. vol.41 no.4 Bahía Blanca oct. 2011
ARTICLES
Molecular weight distributions in ideal polymerization reactors. An introductory review
G.R. Meira and H.M. Oliva
INTEC (Univ. Nac. del Litoral and CONICET), Santa Fe (3000), Argentina. gmeira@santafe-conicet.gov.ar
Escuela de Ingeniería Química, Univ. del Zulia, Maracaibo, Venezuela. holiva@luz.edu.ve
Abstract The ultimate aim of polymerization reaction engineering is the production of polymers with tailor-made properties. An introductory review into this field is presented, with emphasis on the effects on the molar mass distribution (MMD), of the sought combination of polymerization mechanism, reactor type, and reactor control. Three ideal polymerization mechanisms are analyzed: free-radical, "living" anionic, and step-growth. "Living" anionic and step-growth polymerizations are similar in that their growing chains remain reactive while inside the reactor; and for these systems the narrowest MMDs are produced in reactors with narrow residence time distributions (RDT); i.e.: batch or continuous tubular reactors. In contrast, in conventional free-radical polymerizations, the polymer molecules grow in a fraction of a second and thereafter remain inactive while inside the reactor. In this case, the RTD does not affect the MMD, and the homogeneous continuous stirred-tank reactors provide the narrowest MMDs. Representative mathematical models of polymerization reactors are useful for: a) quantifying the interrelationships between their numerous inputs and outputs; and b) developing open- and closed-loop strategies for increasing reactor productivity and product quality.
Keywords Molecular Weight Distribution; Polymerization; Reactor.
I. INTRODUCTION
Synthetic polymers are important materials that find innumerate applications as plastics, composites, rubbers, fibers, adhesives, and coatings. Unlike low molar mass substances where quality is mainly determined by purity, synthetic polymers are mixtures of a large variety of molecular species and morphologies, and therefore are difficult to characterize. The physical properties of polymers (both in the solid and in the melt) depend on complex interrelationships with: a) the molecular structure (described by the distributions of molecular weights, of isomers, of the chemical composition in copolymers, of the molecular topology in long-branched polymers, etc.); and b) the supramolecular morphology (degree of crystallinity, particle size in heterogeneous solids, etc.). "Commodity" thermoplastics and fibers such as polyethylene, polypropilene, PVC, and polystyrene are synthesized in large continuous processes that were mostly developed in the mid-20th Century. In 2007, the World production of synthetic polymers was around 260 million tons, and it is expected to reach 350 million tons by 2015. In volume, the annual production of polymers exceeds that of the 2 most important metals: iron and aluminum. The raw materials for the production of around 95% of all synthetic polymers are non-renewable sources (fossil oil, gas, and coal).
Polymerization Reaction Engineering deals with problems involving the measurement, mathematical modeling, optimization, and control of industrial polymerization processes. It aims at improving both the productivity of the polymerization process and the quality of the produced polymer. Some general references on this area are: Ray (1972), Reichert and Moritz (1989), Hamielec and Tobita (1992), Kiparissides (1996), Ray et al. (2004), Yoon et al. (2004), Meyer and Keurentjes (2005), Villa (2007) and Asua (2007).
Polymers are high molar mass substances characterized by the repetition (neglecting ends, branch junctions, and other minor irregularities) of one or more types of monomeric repeating units. While homopolymers contain a single type of chemical repeating unit, copolymers contain 2 or more. Polymers may be synthetic or natural (such as proteins, carbohydrates, etc.). In spite of their highly sophisticated structures, natural macromolecules are synthesized at ambient temperature and in mild aqueous media, with the aid of specialized catalysts or enzymes (themselves also polymers). In contrast, synthetic polymers are considerably simpler in their chemical and structural characteristics, are mostly soluble in organic solvents, and their syntheses typically require stringent conditions of pressures, temperatures, and solvents.
The total number of repeating units in a chain is the chain length or degree of polymerization. Most synthetic polymers are linear molecules made up of repeating units of functionality 2. Due to their high molar masses and chain entanglements, polymers are solids at room temperature, but may become viscous liquids between 100 and 300 °C. Their average molar masses are typically between 20,000 and 300,000 g/mol. These values are a compromise between mechanical properties (such as elastic modulus, and tensile strength that all increase with the molar mass), and ease of processability in the molten state, favored by a low melt viscosity (or a low molar mass). In contrast, if the polymer is crosslinked or cured, then the material is essentially a single molecule that unless degraded, it will not flow upon increasing the temperature. "Reactors" for producing crosslinked articles are not stirred, and their shapes provide the shape of the final article (e.g.: a mould for producing a rubber tire by vulcanization of a styrene-butadiene prepolymer).
The two main polymerization mechanisms are: chain (or monomer-growth) and step (or polymer-growth). In chain polymerizations, the linear molecule grows by reaction between a monomer and a reactive site on the growing chain end, with the reactive site being regenerated after each propagation step. According to the nature of the reactive site, chain polymerizations are classified into free-radical, anionic, and cationic. Many important polymers such as low-density polyethylene, poly(vinyl chloride) and polystyrenes are produced via free-radical polymerizations. However, from the point of total production, the most important synthetic polymers are obtained via catalyzed chain coordination polymerizations. Examples of these are high-density polyethylene (HDPE), linear low-density polyethylene (LLDPE), isotactic polypropylene, isotactic poly(1-butene), various ethylene-propylene co- and terpolymers, cis-1,4-polybutadiene, and cis-1,4-polyisoprene.
In step polymerizations, all the molecules exhibit reactive chain ends, and the chains grow by reaction between any two molecules (including the monomers). Most step polymerizations are also polycondensations, when a low-molar-mass by-product is generated at each propagation step. Two important industrial polycondensations are the syntheses of Nylon 6,6 (by reaction between hexamethylenediamine and adipic acid), and poly(ethylene terephtalate) or PET (by reaction between terephtalic acid and ethylene glycol).
Most polymerizations are highly exothermic, to compensate for the reduction in entropy produced when transforming many disordered monomer molecules into a reduced number of ordered polymer structures. Thus, most polymerization reactors require an efficient heat extraction system. The heat extraction capacity limit the rate of polymerization of many industrial stirred-tank reactors, due to the reduction in the heat interchange area per unit volume when increasing reaction volume. Most polymerization processes require the monomers to be in a liquid phase. However, some industrial polymerizations also employ gaseous or solid monomers. In bulk polymerizations, the monomer is in liquid state, and the polymer may or may not be soluble in its monomer. Bulk polymerizations can be homogeneous or heterogeneous according to polymer solubility. In addition, bulk polymerizations can be heterogeneous by thermodynamic incompatibility between long chains of different polymers (e.g: a bulk polymerization of styrene in the presence of polybutadiene to produce high-impact polystyrene). In a bulk process, the viscosity of the reaction mixture increases drammatically with conversion; and for this reason final conversions are often limited to ensure an adequate mixing and product extraction. The problems of heat extraction and viscosity increase can be simultaneously solved by carrying out the polymerizations in a dispersed aqueous medium. Suspension and emulsion processes are often employed for the free-radical polymerization of nonpolar monomers (free-radicals are unaffected by water). In contrast, aqueous media are incompatible with anionic polymerizations. Anionic coordination catalysts are mostly supported on magnesium chloride or silica particles, but may also be used in liquid form. Anionic coordination polymerizations are carried out in dispersions or in homogeneous organic media. In coordination polymerizations, the monomer in contact with the catalyst can be either a gas (in the fluidized-bed gas phase process), a pure liquid (in the liquid solution process), or dissolved in a diluent (in the slurry process). Other heterogeneous polymerizations are the interfacial processes for the production of nylons and polycarbonates.
For the random nature of polymerization reactions, all synthetic polymers exhibit a molecular weight distribution, or better: a molar mass distribution (MMD). MMDs totally characterize the molecular macrostructure of linear homopolymers. In long-branched homopolymers and in linear copolymers, the macrostructures respectively include distributions of the number of branches per molecule and of the chemical composition. Apart from the macrostructure, the microstructure of a homopolymer examines the orientation of the different geometrical or optical isomers along the chain (e.g.: the trans content in a dienic monomer or the tacticity of a mono-substituted vinyl monomer). A homopolymer is atactic if there is no systematic or regular configuration of the repeating units along the chain. Atactic polymers are amorphous materials that soften around the glass transition temperature (Tg). In contrast, polymers with chain regularity such as iso- or syndiotactic polypropylene are semi-crystalline when cooled slowly from the melt. Semi-crystalline materials exhibit a (lower) softening temperature at Tg, and a (higher) softening temperature at the melting point (Tm) associated with the crystals fusion. Compared with amorphous polymers, semi-crystalline polymers generally present improved mechanical properties, but are non-transparent.
Copolymers widen the range of properties (such as Tg and Tm) with respect to the base homopolymers; and their microstructure also includes the sequence distributions for each of the comonomers. According to their topology and sequence distributions, copolymers are classified into: a) statistical, when each comonomer exhibits a sequence distribution of known statistics; b) alternate, when the 2 comonomer types are added into the chain in an alternative manner; c) linear block, when long sequences of one comonomer type are followed by long sequences of the other; and d) branched graft, when one of the comonomers constitute the main backbone onto which long-chained branches of the other comonomer are bound.
The processability and end-use properties of uncured polymers are mainly determined at the polymerization stage. This is because it is generally impossible (or technically unviable) to modify the base polymer properties via post-polymerization reactions or unit operations such as fractionation according to molar mass.
The synthesis of complex macromolecules poses major challenges and opportunities, with the expectation that such materials will exhibit distinctive properties and functions (Hawker and Wooley, 2005; Matyjaszewski, 2005). This work is a basic introduction into that field, with emphasis on the effects on the MMDs of the obtained polymers of the different reaction mechanisms, reactor types, and reactor control.
II. MOLAR MASS DISTRIBUTIONS AND AVERAGES
Strictly speaking, MMDs are discrete in the molar masses. In spite of this, MMDs of high polymers are generally represented by continuous curves due to the large number of molar mass types involved, and to the difficulty (or impossibility) of independently determining the exact amount at each molar mass type. In the case of homopolymers, molar masses are restricted to multiples of the repeating-unit molar mass. At each molar mass class M, the ordinates of the MMD can either represent (or be proportional to) the molar fraction (x) or the mass fraction (w). In the former case, the distribution is the number MMD (NMMD) x(M), and its arithmetic mean is the number-average molar mass (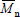 ). In the latter case, the distribution is the weight- or mass-MMD (WMMD) w(M), and its arithmetic mean is the weight-average molar mass (
). In the latter case, the distribution is the weight- or mass-MMD (WMMD) w(M), and its arithmetic mean is the weight-average molar mass (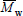 ). The transformation from a NMMD into a WMMD involves multiplying the ordinates of the NMMD by its corresponding abscissas. For this reason, WMMDs are more skewed toward the higher molar masses than NMMDs, and
). The transformation from a NMMD into a WMMD involves multiplying the ordinates of the NMMD by its corresponding abscissas. For this reason, WMMDs are more skewed toward the higher molar masses than NMMDs, and 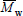 =
= 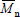 . In homopolymers, the chain length r (= 1, 2, ...) is proportional to the molar mass, and therefore any MMD may be directly transformed into its corresponding Number- or Mass- Chain Length Distribution (NCLD and WCLD, respectively). However, such transformation is impossible for copolymers, because at a given chain length there can be a whole distribution of the chemical composition, and therefore of the molar mass. The arithmetic means of the NCLD and WCLDs are the number- and weight-average chain lengths (
. In homopolymers, the chain length r (= 1, 2, ...) is proportional to the molar mass, and therefore any MMD may be directly transformed into its corresponding Number- or Mass- Chain Length Distribution (NCLD and WCLD, respectively). However, such transformation is impossible for copolymers, because at a given chain length there can be a whole distribution of the chemical composition, and therefore of the molar mass. The arithmetic means of the NCLD and WCLDs are the number- and weight-average chain lengths (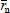 and
and 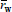 , respectively).
, respectively).
The difference in shapes between a number- and a weight-based MMD is more noticeable when the sample contains a high fraction of low molar mass. Thus, a large difference is observed between x(M) and w(M) in a Schulz-Flory (or "most probable") distribution (Fig. 1 a); while the mentioned difference becomes negligible in a high molar-mass Poisson distribution (Fig. 1 b).
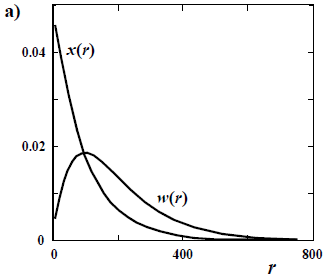
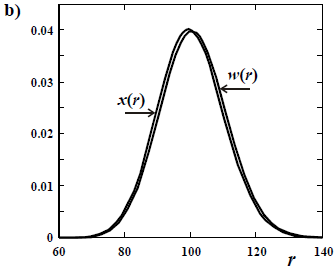
Figure 1. Comparison between a number- and a weight-chain-length distributions of number-average chain length 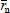 = 100 for: a) a Schulz-Flory distribution; and b) a Poisson distribution. All the distributions are discrete, with values at integers of the chain length r. The ordinates are either the molar fraction x and the weight fraction w.
= 100 for: a) a Schulz-Flory distribution; and b) a Poisson distribution. All the distributions are discrete, with values at integers of the chain length r. The ordinates are either the molar fraction x and the weight fraction w.
At each molar mass Mi, call xi, Ni, Wi,and wi,the corresponding molar fraction, number of moles, mass, and mass fraction, respectively. The following expressions can be written:
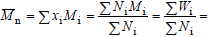 | (1) |
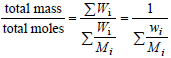 |
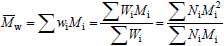 | (2) |
The k-th moment of the NMMD is defined by:
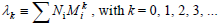 | (3) |
Equations (1-3) yield:
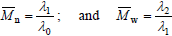 | (4) |
Note that ?0 and ?1 respectively represent the total number of polymer moles and the total number of polymerized monomeric units in a sample. By extension of Eqs (4), the z-average molar mass is defined by:
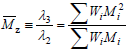 | (5) |
Finally, the viscosity-average molar mass 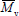 is defined by:
is defined by:
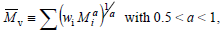 | (6) |
where a is the Mark-Houwink-Sakurada exponent,that depends on the solvent nature and on the temperature of the viscosity measurement. The following inequalities are verified: 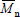 =
= 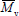 =
= 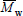 =
= 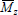 , with the equal signs indicating a uniform or "monodisperse" distribution.
, with the equal signs indicating a uniform or "monodisperse" distribution.
Several analytical techniques have been developed for measuring molar masses. Absolute measurements of 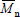 are obtained by membrane osmometry, vapor pressure osmometry, or end-group analysis. Absolute measurements of
are obtained by membrane osmometry, vapor pressure osmometry, or end-group analysis. Absolute measurements of 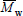 are obtained by light scattering photometry. Capillary viscometry is a relative technique for measuring
are obtained by light scattering photometry. Capillary viscometry is a relative technique for measuring 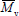 . Size exclusion chromatography (SEC) is the most important technique for measuring the WMMD (Meira et al., 2005; Berek, 2010). These measurements may be either an absolute or relative method, according to whether or not an on-line light-scattering sensor is included in addition to the main concentration (or mass) detector.
. Size exclusion chromatography (SEC) is the most important technique for measuring the WMMD (Meira et al., 2005; Berek, 2010). These measurements may be either an absolute or relative method, according to whether or not an on-line light-scattering sensor is included in addition to the main concentration (or mass) detector.
The ratio D = 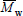 /
/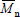 = 1 is called the dispersity, dispersity index, or polydispersity (with the former term being preferred by IUPAC). The following relationship may be proven:
= 1 is called the dispersity, dispersity index, or polydispersity (with the former term being preferred by IUPAC). The following relationship may be proven:
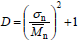 | (7) |
where sn is the standard deviation of the NMMD (an absolute measure of the distribution breadth). From Eq. (7), it follows that (D - 1) is a measure of the ratio between the absolute breadth of a NMMD and its arithmetic mean. Thus, D increases when broadening a NMMD while maintaining a constant 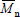 ; but it remains constant when both sn and
; but it remains constant when both sn and 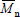 are simultaneously increased or decreased in the same proportion. Dispersities between 1.004 and 1.2 are typical of the narrow MMDs produced by living anionic polymerization (Lee et al., 2000). Dispersities between 1.5 and 3.0 are typical of conventional free-radical polymerizations. Dispersities of 20 or higher are typical of polyolefins obtained via Ziegler-Natta catalysts.
are simultaneously increased or decreased in the same proportion. Dispersities between 1.004 and 1.2 are typical of the narrow MMDs produced by living anionic polymerization (Lee et al., 2000). Dispersities between 1.5 and 3.0 are typical of conventional free-radical polymerizations. Dispersities of 20 or higher are typical of polyolefins obtained via Ziegler-Natta catalysts.
III. IDEAL POLYMERIZATION MECHANISMS IN BATCH REACTORS AND THEIR MOLAR MASS DISTRIBUTIONS
Polymerization chemistry is a complex and well-established discipline (Carraher, 2000, Matyjaszewski and Davis, 2002, and Odian, 2004). In this review, we shall limit to the 3 more basic and representative polymerization mechanisms leading to linear homopolymers: conventional free-radical (Table 1a), "living" anionic (Table 1b), and step growth (Table 1c).
Table 1: Basic Polymerization Mechanisms for the Synthesis of Linear Homopolymers.

The Nomenclature is as follows. In Table 1a: M = Monomer, I = chemical initiator, 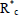 = primary initiator radical,
= primary initiator radical, 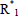 = activated monomer or free-radical of unit chain length,
= activated monomer or free-radical of unit chain length,  ,
, 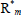 = free-radical of chain lengths n, m, Pn = dead polymer of chain length n, S, S* = solvent and solvent radical, and T, T* = chain transfer agent and corresponding radical. In Table 1b: M and I are as before,
= free-radical of chain lengths n, m, Pn = dead polymer of chain length n, S, S* = solvent and solvent radical, and T, T* = chain transfer agent and corresponding radical. In Table 1b: M and I are as before, 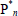 = reactive anion of chain length n, and K = deactivating (or "killing") agent. In Table 1c:
= reactive anion of chain length n, and K = deactivating (or "killing") agent. In Table 1c: 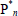 = linear polymer molecule of chain length n, with
= linear polymer molecule of chain length n, with 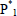 representing the bifunctional monomer as a special case, and E = condensation product (e.g.: water and methanol).
representing the bifunctional monomer as a special case, and E = condensation product (e.g.: water and methanol).
Note that while Tables 1a and 1b represent the basic schemes of chain (or monomer-growth) polymerizations, Eq. (22) of Table 1c represents the base reaction of a step (or polymer-growth) polymerization. Also, note that the anionic mechanism of Table 1b can be considered as a subset of the free-radical mechanism of Table 1a. Neglected in Table 1, are side reactions and reactions with the dead polymer. Also, all the reactions of Table 1 have been assumed simple and bimolecular (except for Eq. 8), and irreversible (except for Eq. 22). In reality, many stages of Table 1 involve complex mechanisms; e.g.: the propagation steps in a gas-solid Ziegler-Natta coordination polymerization for the synthesis of polypropylene; the ring-opening polymerization of e-caprolactam for producing Nylon 6; and the production of primary initiator radicals at low temperatures via redox initiation systems.
Consider now more detailed descriptions of the reaction mechanisms of Table 1; together with the resulting MMDs and averages when such mechanisms are carried out in isothermal and Homogeneous Batch Reactors (HBRs). Figure 2 presents the typical evolutions of the number-average chain length 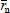 with conversion; and Figs. 3-6 present the theoretical MMDs. For a comprehensive description of theoretical MMDs produced in batch polymerizations, see Peebles (1971).
with conversion; and Figs. 3-6 present the theoretical MMDs. For a comprehensive description of theoretical MMDs produced in batch polymerizations, see Peebles (1971).
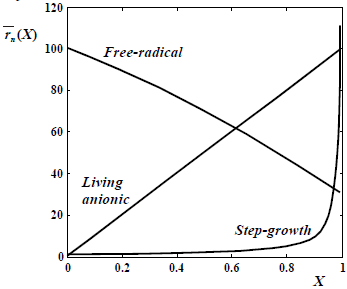
Figure 2. Typical evolutions of the number-average chain-length  with conversion X, according to the base polymerization mechanisms.
with conversion X, according to the base polymerization mechanisms.
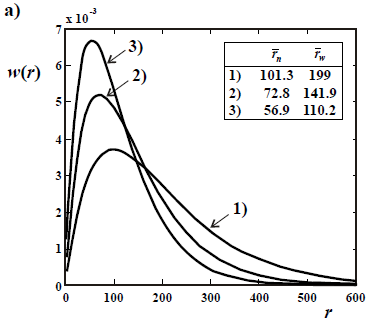
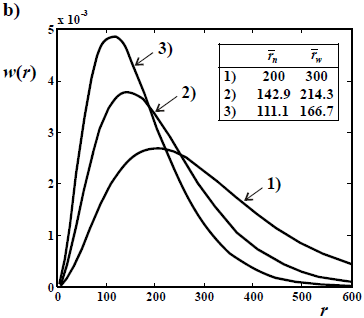
Figure 3. Theoretical WCLDs of the instantaneously-produced linear dead polymer obtained in an ideal, batch, and free-radical polymerization by disproportionation or chain transfer (a), and by recombination (b).
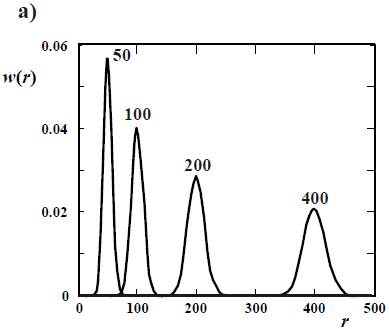
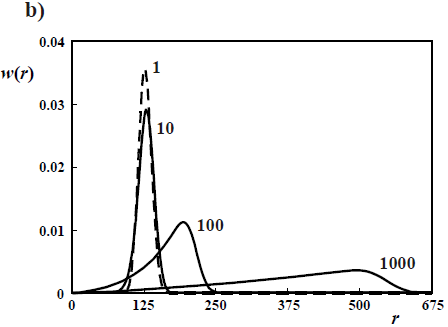
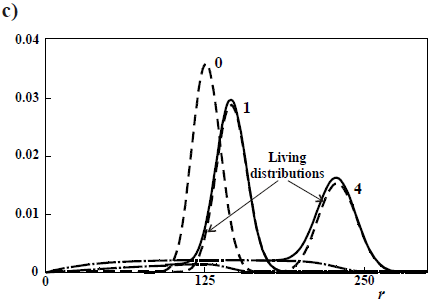
Figure 4. Theoretical WCLDs of linear polymers obtained through ideal anionic polymerizations carried out in batch reactors. a) Poisson distributions obtained with rapid initiation and no termination. b) Gold distributions of a living polymer obtained by slow initiation and no termination. c) WCLDs obtained with rapid initiation and termination by the "killing" agent K (Eq. 21).
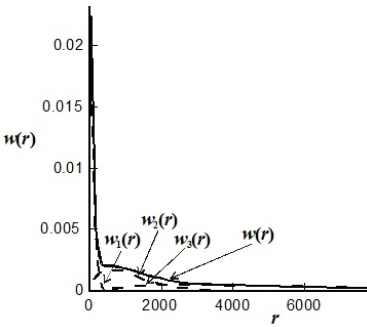
Figure 5. Weight-chain length distribution of a polyolefin made with a coordination catalyst containing three different active-site types. The total distribution (of D = 16.3) is composed of 3 Schulz-Flory distributions with 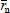 = 50, 600, and 3000, of weight fractions 0.3, 0.3, and 0.4, respectively.
= 50, 600, and 3000, of weight fractions 0.3, 0.3, and 0.4, respectively.
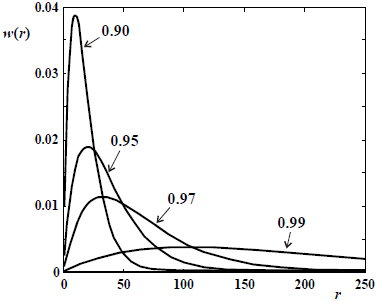
Figure 6. Schulz-Flory WCLDs of linear polymers obtained in ideal step polymerizations carried out in batch reactors. The curve parameter is the extent of reaction (X).
In Fig. 2, note that conventional free-radical polymerization enable to produce high polymers at very low monomer conversions. In contrast, in step-growth polymerizations very high extents of reaction (or conversion of the initial reactive groups) are required for obtaining a high polymer.
In conventional free-radical polymerizations (Table 1a), there is a slow but continuous generation of primary initiator radicals 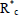 , typically via homolytic cleavage of an initiator molecule such as a peroxide (Eq. 8). Not all primary initiator radicals initiate a polymer chain, and for this reason an efficiency factor is normally introduced into the kinetics of Eq. (9). The decomposition rate of the initiator is generally slow, to ensure a permanent generation of free-radicals along the reaction. The total concentration of free-radicals is low (in the order of 10-7 M), and it results from a balance between rates of generation (Eqs 8 and 9) and rates of deactivation (Eqs 12 and 13). When termination occurs by disproportionation (Eq. 12), two dead polymer molecules are generated, with one of them containing a terminal double bond. In contrast, a single dead polymer molecule is produced by termination recombination (Eq. 13). Chain transfer reactions can occur to the monomer M (Eq. 14), to the solvent S (Eq. 15), or to a specially-added chain transfer agent T (Eq. 16); and the new activated species may or may not reinitiate a new growing chain. Transfer reactions terminate growing chains but do not reduce the total concentration of free-radicals. Their effect is to lower the average molar masses, with generally a small effect on polymerization rate.
, typically via homolytic cleavage of an initiator molecule such as a peroxide (Eq. 8). Not all primary initiator radicals initiate a polymer chain, and for this reason an efficiency factor is normally introduced into the kinetics of Eq. (9). The decomposition rate of the initiator is generally slow, to ensure a permanent generation of free-radicals along the reaction. The total concentration of free-radicals is low (in the order of 10-7 M), and it results from a balance between rates of generation (Eqs 8 and 9) and rates of deactivation (Eqs 12 and 13). When termination occurs by disproportionation (Eq. 12), two dead polymer molecules are generated, with one of them containing a terminal double bond. In contrast, a single dead polymer molecule is produced by termination recombination (Eq. 13). Chain transfer reactions can occur to the monomer M (Eq. 14), to the solvent S (Eq. 15), or to a specially-added chain transfer agent T (Eq. 16); and the new activated species may or may not reinitiate a new growing chain. Transfer reactions terminate growing chains but do not reduce the total concentration of free-radicals. Their effect is to lower the average molar masses, with generally a small effect on polymerization rate.
The lifetime of a growing radical is 1 s or less, and this period is negligible compared to the total reaction time. Chain lengths result from a competition between rate of propagation and rates of termination; noting that termination by recombination doubles the chain length of the dead polymer with respect to the growing radicals. High molar-mass polymer is generated from the start of the polymerization. Also, the average molar masses change moderately along the reaction, and are little related to monomer conversion. When monomer consumptions are faster than initiator consumptions, then the average molar masses will tend to decrease with conversion (see Fig. 2). However, such tendency may be counter-arrested by: i) formation of long chain branches and/or crosslinking; and/or ii) an increased diffusion control of macroradicals (the "gel" or Trommsdorf effect), that slows the effective rate of recombination termination with respect to propagation due to increased viscosity. Branching reactions onto the accumulated polymer are not included in Table 1, but can be produced by propagation with the accumulated polymer containing terminal double bonds and/or by intra- or intermolecular chain transfer to the polymer and subsequent chain growth. For long-branched homopolymers produced by free-radical attack onto the accumulated polymer, several mathematical models have been developed that estimate the evolution of the distributions of molar masses and branching; e.g.: Pladis and Kiparissides (1998), Iedema and Hoefsloot (2002) and Krallis and Kiparissides (2007). For a bulk free-radical homopolymerization, the Tromsdorff effect on the evolving MMD was modelled by Verros et al. (2005).
In the absence of branching, the instantaneously-produced MMD ideally exhibits: i) a Schulz-Flory distribution with D  2 for the fraction of free-radicals that terminate by disproportionation or chain transfer (Fig. 3a); and ii) a Schulz-Zimm distribution with D
2 for the fraction of free-radicals that terminate by disproportionation or chain transfer (Fig. 3a); and ii) a Schulz-Zimm distribution with D  1.5, for the fraction of free-radicals that terminate by recombination (Fig. 3b). When both termination steps are present, then the dispersity of the instantaneously-produced polymer falls between 1.5 and 2. The MMD of the total accumulated polymer is obtained by integration of the instantaneous distributions, with appropriate weighting factors. Due to the varying average molar masses, the final dispersity of the accumulated MMD is typically 3 or higher. In Fig. 3, the curves 1) represent 2 possible initial and instantaneous WCLDs (of
1.5, for the fraction of free-radicals that terminate by recombination (Fig. 3b). When both termination steps are present, then the dispersity of the instantaneously-produced polymer falls between 1.5 and 2. The MMD of the total accumulated polymer is obtained by integration of the instantaneous distributions, with appropriate weighting factors. Due to the varying average molar masses, the final dispersity of the accumulated MMD is typically 3 or higher. In Fig. 3, the curves 1) represent 2 possible initial and instantaneous WCLDs (of 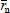 = 101 in a; and
= 101 in a; and 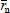 = 200 in b). Then, the average molar masses are assumed to decrease with conversion, yielding the distributions of curves 2) and 3). Note that the
= 200 in b). Then, the average molar masses are assumed to decrease with conversion, yielding the distributions of curves 2) and 3). Note that the 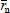 values of Fig. 3a double those of Fig. 3b.
values of Fig. 3a double those of Fig. 3b.
A Schulz-Flory WCLD is represented by (Flory, 1953):
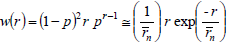 | (23) |
where p is either an extent of reaction or a reaction probability. In Eq. (23), the first equality indicates the exact solution, and the second equality indicates a limiting solution that is accurate for high values of 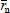 (e.g.: greater than 100). Similarly, Schulz-Zimm WCLDs are represented by (Schulz, 1939):
(e.g.: greater than 100). Similarly, Schulz-Zimm WCLDs are represented by (Schulz, 1939):
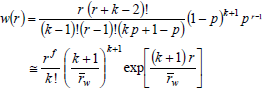 | (24) |
where k is the degree of coupling (i.e.: the number of independently growing chains required to form a single dead chain). With k = 2, D = 1.5 at high degrees of polymerization. With k = 1, the Schulz-Zimm distribution reduces to a Schulz-Flory distribution of D  2.
2.
In spite of the industrial importance of conventional free-radical polymerizations, these mechanisms do not enable an independent control of molecular weights and polymerization rate; and are incapable of producing block copolymers by sequential addition of comonomers. These limitations are at present being circumvented in the so-called "living" or controlled free-radical polymerizations (Matyjaszewski, 2005). In these novel mechanisms, termination by recombination is almost eliminated via introduction of additional reversible reactions that protect the growing free-radicals from each other. Ideally, controlled free-radical polymerizations behave as ideal "living" anionic polymerizations in the absence of termination and with fast initiation. Controlled radical polymerizations are incipiently being employed by industry for the production of specialty polymers with well defined molecular structures. Controlled free-radical polymerizations are outside the scope of this article. However, a large number of publications have been published on: a) their mathematical modelling (e.g.: Monteiro, 2005; Chaffey-Millar et al., 2005; Tobita, 2006); and b) on the production of tailor-made MMDs (e.g.: Kaminski-Lenzi et al., 2005 and Göbelt, 2006).
In living anionic polymerizations (Table 1b), bimolecular termination between living ends is avoided because anions repel each other. Typical initiators are alkyl lithium compounds. Unfortunately, anionic polymerizations require high purity conditions to avoid termination by impurities such as water and acids (Eq. 21). In addition, anionic polymerizations are restricted to relatively few vinyl monomers; and the reactions must be carried out in a solution of organic solvents (that must be recuperated after the synthesis). In the absence of termination and with fast initiation, the total moles of growing anions remain constant and equal to the initial moles of initiator. Under these conditions, 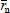 of the accumulated polymer becomes directly proportional to the monomer conversion (see Fig. 2), and its value is given by the ratio between the moles of reacted monomer and the initial moles of initiator. Furthermore, if all the living ends grow simultaneously and at the same rate, then the MMDs become the narrowest possible of synthetic polymers: the Poisson distributions of Fig. 4 a). At high molar masses, a Poisson WCLD is described by the expression:
of the accumulated polymer becomes directly proportional to the monomer conversion (see Fig. 2), and its value is given by the ratio between the moles of reacted monomer and the initial moles of initiator. Furthermore, if all the living ends grow simultaneously and at the same rate, then the MMDs become the narrowest possible of synthetic polymers: the Poisson distributions of Fig. 4 a). At high molar masses, a Poisson WCLD is described by the expression:
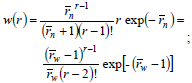 | (25) |
with 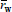 = 1 +
= 1 + 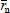 . Figure 4a presents 4 Poisson distributions, where the curve parameters are the number average chain lengths (
. Figure 4a presents 4 Poisson distributions, where the curve parameters are the number average chain lengths (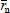 ), that increase with monomer conversion. For increasing
), that increase with monomer conversion. For increasing 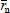 values, note that while the absolute breadth of the distributions (represented by the standard deviation sn) increases, the dispersity D decreases.
values, note that while the absolute breadth of the distributions (represented by the standard deviation sn) increases, the dispersity D decreases.
With slow initiation with respect to propagation but no killing, then the Poisson distributions turn into the Gold distributions of Fig. 4b (Gold, 1958). In Fig. 4b, the curve parameters are the ratios kp/ki (see Eqs 18-20). With kp/ki = 1, the Poisson distribution is obtained. With very slow initiation with respect to propagation (kp/ki = 1000 and higher), then the WCLD tends to a triangular shape with D  1.33, while the corresponding NCLD tends to a rectangular shape.
1.33, while the corresponding NCLD tends to a rectangular shape.
Figure 4c presents the case of a rapid initiation with respect to propagation, but with deactivation of living ends (Eq. 21). In Fig. 4c, all the distributions exhibit a common 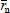 = 125, and the curve parameters are the ratios kt/kp (see Eqs 18-20), for an initial recipe [M]°/ [K]° = 500. Without termination(kt/kp = 0), a Poisson distribution is obtained. With termination, the total WCLD (in continuous trace) contains 2 fractions: a lower molar mass tail of dead polymer (in long traces) and a high molar mass peak of a living polymer (in short traces). At the limit when all the living ends are deactivated, then the dead polymer exhibits a Schulz-Flory distribution. Apart from the production of narrow homopolymers, living anionic polymerizations also enable the synthesis of 'tailor-made' structures such as block copolymers, star copolymers, and telechelic polymers. For example, an ABC triblock copolymer can be obtained by sequential addition of comonomers A, B, and C along the reaction.
= 125, and the curve parameters are the ratios kt/kp (see Eqs 18-20), for an initial recipe [M]°/ [K]° = 500. Without termination(kt/kp = 0), a Poisson distribution is obtained. With termination, the total WCLD (in continuous trace) contains 2 fractions: a lower molar mass tail of dead polymer (in long traces) and a high molar mass peak of a living polymer (in short traces). At the limit when all the living ends are deactivated, then the dead polymer exhibits a Schulz-Flory distribution. Apart from the production of narrow homopolymers, living anionic polymerizations also enable the synthesis of 'tailor-made' structures such as block copolymers, star copolymers, and telechelic polymers. For example, an ABC triblock copolymer can be obtained by sequential addition of comonomers A, B, and C along the reaction.
In coordination polymerizations involving Ziegler-Natta, Phillips, or metallocene catalysts, the catalyst influences the monomer addition during chain growth, and this affects the rates of propagation, chain transfer, and termination reactions. Ziegler-Natta and metallocene catalysts require activation by cocatalysts like alkyl aluminum or alkyl aluminoxane compounds that control the oxidation state of the transition metal. The mechanism is similar to that of living anionic polymerizations in that the growing chains exhibit relatively long lifetimes (typically, between 100 and 106 s). Each different catalyst has its own set of kinetic parameters. Polymers produced using heterogeneous Ziegler-Natta catalysts exhibit broad MWDs, with dispersities of 10 or higher, depending on the catalyst. These large dispersities are the result of chain transfer reactions combined with a multiplicity of catalyst active sites (Kissin, 1993). Under constant reaction conditions, each catalyst site produces a polymer with a Schulz-Flory distribution of different averages, and the total MMD is a weighted combination of such individual distributions (Kissin, 1985). This situation is illustrated in Fig. 5. Soares (2001) reviewed the mathematical modelling of polyolefins obtained by coordination polymerization.
In its most basic level, step polymerizations are represented by a single propagation reaction (Eq. 22 in Table 1c). For linear polymers, bifunctional monomers are required, and intramolecular reactions must be avoided. In Eq. (22), the condensation molecule E may or may not be generated. In its simplest form, the monomer molecule contains 2 types of reacting groups (e.g.: an aminoacid); and all the growing chains also exhibit the same reacting groups (an acid and an amine) at their chain ends. Alternatively, 50:50 mixtures of 2 comonomer types with identical reacting groups are employed. For example, in a reaction between a diamine and a diacid, the reaction mixture will contain 3 types of molecules: aminoacids, diamines, and diacids. In the case of reversible polycondensations, the equilibrium can be displaced toward the high molar masses by extraction of E (see Eq. 22). Unlike the case of chain reactions, the monomer is rapidly consumed in step polymerizations. Step-growth reactions are similar to living anionic in that all the molecules remain potentially reactive (or "living") while inside the reactor, and in that the average molar masses increase monotonically with conversion, but in a highly nonlinear fashion (Fig. 2). Ideal step polymerizations of bifunctional monomers produce linear polymers with Schulz-Flory MMDs. Figure 6 presents several of such distributions at different extents of reaction. Note that (unlike the case of chain reactions), the unreacted monomer remains in the product, and it is always the most abundant species from the point of view of number (see NCLD of Fig. 1a).
So far, we have have presented the theoretical MMDs produced in ideal, isothermal, and homogeneous batch polymerizations. In spite of their industrial importance, heterogeneous processes are outside the scope of the present article. In particular, the mathematical modelling of free-radical emulsion processes has been reviewed on several occasions: MacGregor et al. (1984b), Saldivar et al. (1998), Gao and Penlidis (2002) and Zhang and Feng (2010). Many other heterogeneous processes have also been investigated. For example, Karode et al. (1997) modelled a heterogeneous interfacial polycondensation for the synthesis of Nylon 6,10.
The mathematical modelling of polymerization reactors is useful for: a) quantifying the interrelationships between their numerous inputs and outputs; and b) developing open- and closed-loop control strategies for increasing reactor productivity and product quality.
For producing prespecified MMDs, several alternatives to batch isothermal polymerizations are possible. In a first level of flexibilization, nonisothermal batch reactions can be used (see, for example Crowley and Choi, 1998, for a batch free-radical solution polymerization of methyl methacrylate). In what follows, the use of semi-batch and continuous polymerization reactors will be considered.
IV. MOLAR MASS DISTRIBUTIONS in SEMI-BATCH POLYMERIZATIONS
The semi-batch addition of reagents along a polymerization considerably increases the flexibility of batch reactors for producing prespecified MMDs. For a free-radical polymerization of acrylamide in aqueous solution, Kreft and Reed (2009) developed semi-batch control strategies for producing multimodal MMDs. For emulsion polymerizations, many publications have developed semi-batch addition policies of reagents for controlling the MMD and other chemical characteristics; e.g.: Vieira et al. (2002), Arizmendi and Leiza (2002) and Srour et al. (2009). For obtaining a broad MMD polyurethane without formation of gel, Zavala et al. (2005) developed a strategy that involves the additions of a diol and a diamine along the reaction.
The ability of living anionic polymerizations for producing narrow MMDs with prespecified average molar masses, make these mechanisms ideal for controlling the MMDs of homopolymers and of block copolymers with prespecified distributions in each of the blocks. For a polystyrene homopolymer, Alassia et al. (1988) proposed a method for obtaining almost any MMD shape, by controlled deactivation of a living anionic polymerization. The strategy involves the application of 2 simultaneous flow profiles: i) a monomer feed into the reactor; and ii) a reactor outlet flow into a reception vessel where instantaneous deactivation takes place. At the end of the semi-batch operation, the reactor is empty and the reception vessel contains the required MMD (Alassia et al., 1988).
V. MOLAR MASS DISTRIBUTIONS IN CONTINUOUS POLYMERIZATIONS
Industry employs a large variety of batch, semi-batch, and continuous polymerization reactors. For continuous reactors operating in the Steady State (SS), then (for comparison reasons) it is convenient to classify them according to their residence-time distribution (RTD).
Continuous Piston-Flow Tubular Reactors (CPFTRs) exhibit the narrowest RTDs, and in the limit they are dynamically equivalent to Homogeneous Batch Reactors (HBRs), with time replaced by distance along the tube. In contrast, single Homogeneous Continuous Stirred-Tank Reactors (HCSTRs) exhibit the widest RTDs. Intermediate RTDs are obtained when a single HCSTR is replaced by a series 2 or more HSTRs of the same total volume.
Since HBRs are equivalent to SS CPFTRs, then homogeneous semi-batch reactors are equivalent to SS CPFTRs with SS addition of reagents along the tube. The articles by Asteasuain and Brandolin (2007), and Asteasuain et al. (2008) are examples of SS optimizations of tubular reactors with intermediate feeds for producing tailored MMDs. For polymerizations carried out in tubular reactors that do not verify the ideal piston-flow condition, then computational fluid dynamics (CFD) methods have been applied for simulating the radial profiles of flow velocity, temperature, and polymer molecular weights (Meszena and Johnson, 2001).
In Homogeneous Batch Reactors (HBRs), the concentration of reagents and products vary in time but not in space. In HCSTRs operated in the SS, the concentrations remain constant both in time and in space. High viscosity systems may cause segregation by inadequate mixing at a molecular level(or micromixing). Polymerizations may be segregated either due to inadequate micromixing or because the process itself is heterogeneous (e.g.: an emulsion polymerization). In an ideal Segregated Continuous Stirred-Tank Reactor (SCSTR), the fluid phase is regarded as subdivided into many small isolated compartments. Each compartment contains a large number of molecules that are permanently confined within its limits. Thus, individual compartments function as miniature batch reactors of different residence times in the flow reactor. The compartments themselves are assumed to be ideally mixed, and this leads to a macromixing, despite total segregation of molecules in the different compartments. In this case, the RTD for the set of compartments of a SCSTR coincides with the RTD of a HCSTR. A macroscopic mean taken over all the compartments in the effluent stream and in the reactor itself would show constant concentrations and temperatures both in space and in time. However, a probe capable of microscopic sampling of individual compartments would reveal concentrations that varied in a statistical manner from one compartment to another.
For the ideal mechanisms of Table 1, the first row of Table 2 summarizes the previously-discussed results for HBRs, or equivalently for CPFTRs operating in the SS. Such results are compared with the MMDs obtained in HCSTRs and SCSTRs (second and third rows of Table 2). Consider first the case of HCSTRs. According to Denbigh (1965), two opposing factors influence the MMDs obtained in a HCSTR. On the one hand, the constant concentrations of reagents and products will tend to narrow the distribution with respect to the batch. On the other hand, the broad RTD will lead to broaden the MMD. In a free-radical polymerization, a growing radical produces a dead polymer molecule in a fraction of a second, and thereafter such molecule remains inert until its reactor exit. Thus, the growing period is negligible with respect to the average residence time of an industrial HCSTR, the constant composition factor dominates, and a relatively narrow MMD is produced. This distribution coincides with the MMD instantaneously-produced in a HBR for the same concentrations of reagents and products. If however branching reactions with the accumulated polymer were admitted (not considered in Table 1), then the accumulated polymer would remain reactive while inside the reactor, and the RTD would considerably broaden the MMD with respect to the HBR. When eithe a step-growth or a living anionic polymerization is carried out in a HCSTR, then the chains continuously grow while inside the reactor, and the growth is assumed to stop at the reactor outlet. Thus, the lifetimes of the growing chains are directly affected by the RTD, and the resulting MMDs are considerably broader that in HBRs. With ideal anionic polymerizations, the MMDs vary from Poisson- or Gold- distributions in HBRs, to Schulz-Flory distributions in HCSTRs. In spite of this large increase in the distribution breadth, single HCSTRs are commercially employed for living anionic polymerizations, due to the higher efficiencies of HCSTRs with respect to HBRs, together with a reduced contamination by impurities in a more closed and controlled environment. In contrast, single HCSTRs are not employed with step polymerizations because: i) very high conversions are required for high polymers, and this would imply unacceptably high viscosities in bulk polymerizations; and ii) extremely broad MMDs are produced, and for example for 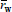 ? 1000, the dispersity is over 40!.
? 1000, the dispersity is over 40!.
Table 2: MMDs of Linear Polymers for Different Combinations of Ideal Polymerization Mechanisms and Reactor Types (after Hamielec and Tobita, 1992).
Finally, consider the SS operation of SCSTRs (last row of Table 2). Each individual compartment works as a miniature batch reactor, and the global RTD E(t) coincides with the RTD of a HCSTR, i.e.:
 | (26) |
where t is the mean residence time. In free-radical polymerizations, the effect of segregation is to broaden the MMD with respect to a HBR of total reaction time t. Thus, while HCSTRs produce the narrowest possible MMDs (in general, a Schulz-Zimm distribution with k = 1, 2, or both), such distributions become considerably broader in SCSTRs. In living anionic polymerizations, the rate of polymerization is first order with respect to the monomer, and therefore both the HCSTR and SCSTR exhibit the same average polymerization rates and conversions. Segregation inhibits total molecular mixing, whereas in a HCSTR all the molecules are distributed in time according to Eq. (23). In SCSTRs, Eq. (23) is only true with respect to the compartments, but each compartment has a large number of molecules with equal residence times. Thus, the MMDs obtained in SCSTRs with living anionic mechanisms are subject to less broadening than in HCSTRs. At very low conversions, the monomer concentration remains essentially constant, and the MMDs are almost identical in the 3 reactor types. At increased conversions, the effect of RTD diminishes. At 100% conversion, the lifetimes of the active species are shorter than the mean residence time, and therefore the MMD tends to the distribution of a HBR. At intermediate conversions, the MMDs obtained in SCSTRs with ideal living anionic mechanisms are intermediate between Schulz-Flory and Poisson. This intermediate distribution is similar to that obtained in batch anionic polymerizations with termination and rapid initiation (see Fig. 4c). Finally, consider the case of step-growth polymerizations carried out in SCSTRsoperating in theSS. Segregation reduces the amount of polymer with very high or very low molar mass, and therefore the molar mass dispersities obtained in SCSTRs are between the limiting values obtained in CPFTRs/BRs and HCSTRs.
Random copolymers are generally obtained by chain-growth copolymerization, with intermediate properties with respect to their parent homopolymers. Normally, the aim is to produce narrow Chemical Composition Distributions (CCDs); and to this effect the composition must be maintained constant along the reaction. Except for the few examples where the reactivity ratios of both comonomers are close to unity, batch reactors generally produce broad CCDs, due to varying copolymer compositions along the reaction. Several strategies have been proposed to solve this problem. For example, the comonomers mixture can be slowly added along the batch reaction to induce a starved semi-batch policy, with almost complete instantaneous conversion of both comonomers. However, a simpler solution is to carry out the copolymerization in a HCSTR. In this case, a constant copolymer composition is ensured by the constant concentrations of reagents and products.
VI. MONITORING AND CONTROL OF POLYMERIZATION REACTORS
Commercial polymerizations aim at obtaining consistent polymer properties at increasing productivities, in safe and economical operations. Polymerization processes typically consist of 3 stages: preparation, polymerization, and separation. In the preparation stage, the reagents are purified and mixed. The purification of monomer and initiator are vital operations, since small amounts of impurities can importantly affect the reaction. In the polymerization stage, the heat exchange and the system viscosity play crucial roles that affect not only the (mass, heat, and momentum) balances, but also the quality of the mixing and the RTD. In the final separation stage, the required polymer purity and state is achieved through appropriate thermal and mechanical operations that include recycling the unreacted monomer and solvent. Even though the main mechanical, physical and chemical properties of a polymer are acquired at the reaction stage, further modifications can be introduced during the separation stage and processing.
Several articles have comprehensively reviewed the field of monitoring and control of polymerization reactors; e.g.: Mac Gregor et al. (1984a), Eliçabe and Meira (1988), Richards and Congalidis (2006) and Hukkanen et al. (2007). This last section is a short introduction into such field, with emphasis on the control of molar mass averages and distributions.
Polymerization reactors are highly multivariate dynamical systems, and the complex interrelationships between their inputs and outputs are in many cases only scarcely known. For example, Fig. 7 lists the numerous variables involved in the quality control of a bulk polymerization of styrene in the presence of polybutadiene for the production of high-impact polystyrene (HIPS). The input variables (left-hand side of Fig. 7) are selectable or modifiable by the design or process engineer. The output quality variables (right-hand side of Fig. 7) have been classified into "chemical" and "physical". "Chemical" variables are closely related to the polymerization process. "Physical" variables constitute the base material specifications for its processability and end-use performance.
Figure 7. Main process variables of a bulk polymerization of styrene in the presence of polybutadiene for the production of high-impact polystyrene (HIPS). The input variables are in the left column, and the polymer quality variables are in the right column. The "chemical" quality variables (or polymer microstructure) are closely associated with the polymerization stage, while the "physical" quality variables (or macroscopic polymer characteristics) define the processability and end-use properties of the material. The quality variables may be further modified in the final article by addition of additives and loads and through processing operations such as injection molding. (Taken from Meira et al., 2007).
The need of monitoring is obvious in polymerization processes; and in particular rapid on-line monitoring is highly desirable for an effective quality control. However, most quality measurements such as composition, particle size, or melt flow index (MFI) are carried out off-line, and in a discontinuous fashion. Furthermore, many important variables such as average molar masses and degrees of branching are generally not measured at all, not even off-line.
The problems of reactor productivity and selectivity, process stability and safety, transient control, and start-up procedures should be taken into consideration at the design stage. Reactor productivity studies aim at increasing the final monomer conversion without affecting quality, and at reducing the off-spec product generated in transitions between steady-states. Reactor selectivity studies aim at improving polymer quality.
For an effective reactor design, optimization and control, the results of costly experimentation must be combined with simulation results from representative mathematical models. Mathematical models also help in quantifying the numerous interrelationships between the process inputs and outputs. Mathematical models may be derived from detailed (mass and energy) balances, or through empirical input-output (or black-box) techniques. Detailed balances for batch or HCSTRs generally consist of sets of non-linear, time-invariant, ordinary first-order differential equations combined with sets of nonlinear algebraic equations, such as:
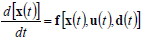 | (27) |
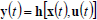 | (28) |
where x(t) is an n-vector of states, u(t ) is an m-vector of controls or manipulated variables, d(t) is a k-vector of disturbances, and y(t) is a p-vector of measured outputs. Equations (27) and (28) are known as the state and measurement equations, respectively. The state vector x(t) provides information on the time trajectories of the most important reactor variables such as concentrations of reagents, moments of the MMD, temperature, etc.
Due to the complex and highly nonlinear nature of Eqs (27) and (28), the monitoring, optimization, and control of polymerization reactors present many challenging problems. Most industrial control practice is centered on batch reactor sequencing, and on the control of global variables such as temperature and monomer conversion. To this effect, reactor energy balances are useful to infer polymer production rates and monomer conversion. In addition, many academic articles have focused on the quality control of polymerization reactors through the development of optimal operating policies for batch, semi-continuous, and continuous reactors. Since most of such control policies are open-loop, then the real plant performance becomes totally dependent on the accuracy of the employed mathematical model. In spite of the important advances in process control (in particular of nonlinear systems), there are relatively few successful industrial applications of such novel techniques. Two illustrative examples of multivariable and nonlinear control of free-radical polymerizations carried out in CSTRs are given in Prasat et al. (2002) and González and Álvarez (2008).
The periodic operation of continuous polymerization reactors has been investigated in several opportunities as a means of modifying the molecular characteristics of the obtained polymers with respect to those obtained in the SS (Silveston, 1998). For example, free-radical polymerizations carried out in HCSTRs with periodic feed flows of the monomer and the initiator in phase opposition can be used to broaden the MMD with respect to that obtained in the SS (Meira et al., 1979). In contrast, the periodic operation of the initiator and monomer feeds of a living anionic polymerizations enable to produce controlled 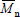 's combined with dispersities both above and below the SS value of 2 (Vega et al., 1991).
's combined with dispersities both above and below the SS value of 2 (Vega et al., 1991).
VII. CONCLUSIONS
The industrial production of synthetic polymers is among the most complex processes of the chemical industry. In addition, the molecular characterization of the obtained polymers is complex, due to the various distributions involved (of the molar masses, chemical composition, degrees of cristallinity, etc.).
In conventional free-radical polymerizations with negligible attack onto the accumulated polymer, the polymer chains grow in a short period with respect to the total polymerization time, and thereafter remain inert. For this reason, HBRs generally produce wider MMDs compared to SS HCSTRs. On the negative side, conventional free-radical polymerizations are inadequate for producing narrow MMDs, the average molar masses are difficult to modify, and block copolymers cannot be synthesized. At present, these limitations are being circumvented with the development of controlled free-radical polymerizations. The constant composition of reagents and products in HCSTRs is also helpful for producing random copolymers of narrow CCDs.
In living anionic and step polymerizations, the growing chains remain active while inside the reactor; and for this reason HBRs (or SS CPFTRs) yield the narrowest possible MMDs. These distributions are broadened when the reaction is carried out in a single HCSTR operating in the SS, due to its broad RTD. For this reason and for the extremely high conversions (and viscosities) required, bulk step polymerizations are not carried out in single HCSTRs.
MMDs of any prespecified shape can in principle be produced by appropriate addition of narrow MMDs of controlled averages. The opposite (i.e.: the narrowing a broad distribution by post-reaction operations) is technically unviable for commodity polymers. Thus, living anionic polymerizations carried out in semi-batch reactors present an unsurpassed flexibility for controlling molecular weights, but this advantage is counterarrested by the experimental difficulties associated with the extreme purities required to avoid deactivation of the living ends. In the case of polyolefins produced by Ziegler-Natta catalysis, the flexibility of living anionic polymerizations is lost, due to the multiplicity of catalyst active sites that result in very broad MMDs and CCDs. This difficulty is at present partially overcome with the development of single-site metallocenic catalysts, where MMDs dispersities as low as 2 have been produced.
Polymerization models are helpful for systematizing the interrelationships between the numerous inputs and outputs of an industrial plant. Their ultimate goal is the a priori calculation of the required recipe, reactor conditions, and control procedure for increasing productivity while simultaneously improving polymer quality. In theoretically-developed open-loop strategies, the use of feed-back control loops is helpful for compensating model errors as well as experimental unknowns such as the concentration of impurities.
ACKNOWLEDGEMENTS
The authors acknowledge the financial support received by CONICET and Univ. Nac. del Litoral (Argentina), and by CONDES-LUZ and Univ. del Zulia (Venezuela).
REFERENCES
1. Alassia, L.M., D.A. Couso and G.R. Meira, "Molecular Weight Distribution Control in a Semi-Batch 'Living' Anionic Polymerization. II. Experimental Study," J. Appl. Polym. Sci., 36, 481-494 (1988). [ Links ]
2. Arizmendi, G. and J.R. Leiza, "Molecular weight distribution (soluble and insoluble fraction) in emulsion polymerization of acrylate monomers by Montecarlo simulations," Ind. Eng. Chem. Res., 47, 5934-5947 (2002). [ Links ]
3. Asteasuain, M. and A. Brandolin, "Optimal operation of ethylene polymerization reactors for tailored molecular weight distribution," J. Appl. Polym. Sci., 105, 2621-2630 (2007). [ Links ]
4. Asteasuain, M., M. Soares, M.K. Lenzi, R.A. Hutchinson, M. Cunningham, M., A. Brandolin, J.C. Pinto, and C. Sarmoria, "Living radical polymerization in tubular reactors, 2- Process optimization for tailor-made molecular weight distributions," Macromol. React. Eng., 2, 414-421 (2008). [ Links ]
5. Asua, J.M. Ed., Polymer Reaction Engineering, Blackwell Publishing, Malaysia (2007). [ Links ]
6. Berek, D., "Size exclusion chromatography - A blessing and a curse of science and technology of synthetic polymers," J. Sep. Sci., 33, 315-335 (2010). [ Links ]
7. Carraher, C.E., Polymer Chemistry, M. Dekker Inc., N. York (2000). [ Links ]
8. Chaffey-Millar, H., M. Busch, T.P. Davis, M.H. Stenzel and Ch. Barner-Kowollik, "Advanced computational strategies for modelling the evolution of full molecular weight distributions formed during multiarmed (star) polymerizations," Macromol. Theory Simul., 14, 143-157 (2005). [ Links ]
9. Crowley, T.J. and K.Y. Choi, "Experimental studies on optimal molecular weight distribution control in a batch-free radical polymerization process," Chem. Eng. Sci., 53, 2769-2790 (1998). [ Links ]
10. Denbigh, K.G. Chemical Reactor Theory, Cambridge Univ. Press, Cambridge (1965). [ Links ]
11. Eliçabe, G.E. and G.R. Meira, "Estimation and Control in Polymerization Reactors. A Review," Polym. Eng. & Sci., 28, 121-135 (1988). [ Links ]
12. Flory, P.J., Principles of Polymer Chemistry, Cornell Univ. Press, Ithaca, New York (1953). [ Links ]
13. Gao, J. and A. Penlidis, "Mathematical modeling and computer simulation/database for emulsion polymerizations," Prog. Polym. Sci., 27, 403-535 (2002). [ Links ]
14. Gobelt, B., "Molecular weight distribution in living polymerization,"Progress in Organic Coatings, 55, 189-193(2006). [ Links ]
15. Gold, L., "Statistics of polymer molecular weight distribution for an invariant number of propagating chains," J. Chem. Phys., 28, 91-99 (1958). [ Links ]
16. González, P. and J. Álvarez, "Constructive molecular weight control of continuous homopolymer reactors," Ind. Eng. Chem. Res., 47, 9971-9982 (2008). [ Links ]
17. Hamielec, A.E. and H. Tobita, "Polymerization Processes," Ullmann's Encyclopedia of Industrial Chemistry, VCH Publishers Inc., A21, 305-428 (1992). [ Links ]
18. Hawker, C.J. and K.L. Wooley, "The convergence of synthetic organic and polymer chemistries," Science, 309, 1200-1205 (2005). [ Links ]
19. Hukkanen, E.J., J.G. VanAntwerp and R.D. Braatz, "Identification and control of polymerization reactors," Chap. 1 of Identification and Control, Sánchez-Peña, Quevedo-Casin, and Puig-Cayuela Eds., Springer, 3-41 (2007). [ Links ]
20. Iedema, P.D. and H.C.J. Hoefsloot, "Molecular weight distribution modelling of radical polymerization in batch and continuous reactors with transfer to polymer leading to gel formation," Macromol. Theory Simul., 11, 410-428 (2002). [ Links ]
21. Kaminski-Lenzi, M., M.F. Cunningham, E.L. Lima and J.C. Pinto, "Producing bimodal molecular weight distribution polymer resins using conventional free-radical polymerization," Ind. Eng. Chem. Res., 44, 2568-2578 (2005). [ Links ]
22. Karode, S.K., S.S. Kulkarni, A.K. Suresh and R.A. Mashelkar, "Molecular weight distribution in interfacial polymerization-model development and verification," Chem. Eng. Sci., 52, 3243-3255 (1997). [ Links ]
23. Kiparissides, C. "Polymerization reactor modeling: A review of recent developments and future directions," Chem. Eng. Sci., 51, 1637-59 (1996). [ Links ]
24. Kissin, Y.V., "Isospecific polymerization of olefins with heterogeneous Ziegler-Natta catalysts," Springer-Verlag Inc., New York (1985). [ Links ]
25. Kissin, Y.V., Makromol. Chem.-M. Symp, 66, 83-94 (1993). [ Links ]
26. Krallis, A. and C. Kiparissides, "Mathematical modelling of the bivariate molecular weight-long chain branching distribution of highly branched polymers. A population balance approach," Chem. Eng. Sci., 62, 5304-5311 (2007). [ Links ]
27. Kreft, T. and W.F. Reed, "Predictive control and verification of conversion kinetics and polymer molecular weight in semi-batch free radical homopolymer reactions," European Polymer Journal, 45, 2288-2303 (2009). [ Links ]
28. Lee, W., H. Lee, J. Cha, T. Chang, K.J. Hanley and T.P. Lodge, "Molecular weight distribution of polystyrene made by anionic polymerization," Macromolecules, 33, 5111-5115 (2000). [ Links ]
29. Mac Gregor, J.F., A. Penlidis and A.E. Hamielec, "Control of polymerization reactors: a review," Polym. Process Eng., 2, 179-206 (1984a). [ Links ]
30. MacGregor, J.F., A. Penlidis and A.E. Hamielec, A.E., "Dynamic modelling of emulsion polymerization reactors: a review," Proc. ACS 1984 Summer National Meeting, Philadelphia, USA (1984b). [ Links ]
31. Matyjaszewski, K., "Macromolecular engineering: from rational design through precise macromolecular synthesis and processing to targeted macroscopic material properties," Progress in Polymer Sci., 30, 858-875 (2005). [ Links ]
32. Matyjaszewski, K.; Davis, T.P., Handbook of Radical Polymerization, Wiley-Interscience, New York (2002). [ Links ]
33. Meira, G.R., M. Yossen and J. Vega, "Gel Permeation and Size Exclusion Chromatography," Chap. 26 of Ewing's Analytical Instrumentation Handbook, Third Edition, J. Cazes Ed., CRC Press, 825-867 (2005). [ Links ]
34. Meira, G.R., A.F. Johnson and J. Ramsay, Cap. 11 of Polymerization Reactors and Processes, ACS Symposium Series Vol. 104, J.N. Henderson and T.C. Bouton Eds., American Chemical Society (Washington), 253-266 (1979). [ Links ]
35. Meira, G.R., C.V. Luciani and D.A. Estenoz, "Continuous bulk process for the production of high-impact polystyrene: recent developments in modeling and control," Macromol. React. Eng., 1, 25-39 (2007). [ Links ]
36. Meszena, Z.G. and A.F. Johnson, "Prediction of the spatial distribution of the average molecular weights in living polymerisation reactors using CFD methods," Macromol. Theory Simul. 10, 123-135 (2001). [ Links ]
37. Meyer, T., J. Keurentjes, Eds., Handbook of Polymer Reaction Engineering, Wiley-VCH Verlag GmbH & Co. KGaA, Weinheim (2005). [ Links ]
38. Monteiro, M., "Modeling the molecular weight distribution of block copolymer formation in a reversible addition-fragmentation chain transfer mediated living radical polymerization," J. Polym. Sci. A, Polym. Chem., 43, 5643-5651 (2005). [ Links ]
39. Odian, G., Principles of Polymerization, 4th. Ed., J. Wiley, New York (2004). [ Links ]
40. Peebles, L.H., Molecular Weight Distributions in Polymers, Interscience Pub., New York (1971). [ Links ]
41. Pladis, P. and C. Kiparissides, "A comprehensive model for the calculation of molecular weight-long chain branching distribution in free-radical polymerization," Chem. Eng. Sci., 53, 3315-3333 (1998). [ Links ]
42. Prasat, V, M. Schley, L.P. Russo and B. Wayne Bequette, "Product property and production rate control of styrene polymerization," J. Process Control, 12, 353-372 (2002). [ Links ]
43. Ray, W.H., "On the mathematical modelling of polymerization reactors," J. Macromol. Sci., Revs. Macromol. Chem., C8(1), 1-56 (1972). [ Links ]
44. Ray, W.H., J.B.P. Soares, R.A. Hutchinson, "Polymerization reaction engineering: past, present and future," Macromolecular Symposia, 206, 1-13 (2004). [ Links ]
45. Reichert, K.H. and H.U. Moritz, "Polymer reaction engineering," Vol. 3, Chap. 24 of Comprehensive Polymer Science, G. Allen and J.C. Bevington, Eds., Pergamon Press (1989). [ Links ]
46. Richards, J.R. and J.P. Congalidis, "Measurement and control of polymerization reactors," Comp. & Chem. Eng., 30, 1447-1463 (2006). [ Links ]
47. Saldívar, E., P. Dafniotis and W. Ray, "Mathematical modeling of emulsion copolymerization reactors. I. Model formulation and application to reactors operating with micellar nucleation," J. Macromol. Sci.-Rev Macromol. Chem. Phys., C38, 207-325 (1998). [ Links ]
48. Schulz, G.V., "Uber die Kinetik der Kettenpolymerisationen. V. Der Einfluss verschiedener Reaktionssarten auf die Polymolekularitat," Z. Phisik Chem, B43, 25 (1939). [ Links ]
49. Silveston, P.L., Chap. 14 "Polymerization Reactions," Composition Modulation of Catalytic Reactors, Gordon & Breach Sci. Pub., 498-529 (1998). [ Links ]
50. Soares, J.B.P., "Mathematical modelling of the microstructure of polyolefins made by coordination polymerization: a review," Chem. Eng. Sci., 56, 4131-4153 (2001). [ Links ]
51. Srour, M.H., V.G. Gomes, I.S. Altarawneh and J.A. Romagnoli, "Online model-based control of an emulsion terpolymerisation process," Chem. Eng. Sci., 64, 2076-2087 (2009). [ Links ]
52. Tobita, H., "Molecular weight distribution of living radical polymers. 1 Fundamental distribution, and 2 Montecarlo simulation," Macromol. Theory Simul., 15, 12-22 and 23-31 (2006). [ Links ]
53. Vega, J.R., G.L. Frontini and G.R. Meira, "Optimal periodic control of a continuous 'living' anionic polymerization. III. Presence of impurities in the monomer feed," J. Appl. Polym. Sci., 42, 3181-3193 (1991). [ Links ]
54. Verros, G.D., T. Latsos, and D.S. Achilias, "Development of a unified framework for calculating molecular weight distribution in diffusiion controlled free radical bulk homo-polymerization," Polymer, 46, 539-552 (2005). [ Links ]
55. Vieira, R.A.M., C. Sayer, E.L. Lima and J.C. Pinto, "Closed-loop composition and molecular weight control of a copolymer latex using near-infrared spectroscopy," Ind. Eng. Chem. Res., 41, 2915-2930 (2002). [ Links ]
56. Villa, C., "Reactor modelling for polymerization processes," Ind. Eng. Chem. Res., 46, 5815-5823 (2007). [ Links ]
57. Yoon, W.J., Kim, Y.S., Kim, I.S. and Choi, K.Y., "Recent advances in polymer reaction engineering: modeling and control of polymer properties," Korean J. Chem. Eng., 21, 147-167 (2004). [ Links ]
58. Zavala, V.M., A. Flores-Tlacuahuac and E. Vivaldo-Lima, "Dynamic optimization of a semi-batch reactor for polyurethane production," Chem. Eng. Sci., 60, 3061-3079 (2005). [ Links ]
59. Zhang, B.; Feng, S., "Advances in the modelling and simulation of emulsion polymerization," Int. J. of Modelling, Identification & Control, 11, 262-273 (2010). [ Links ]
Received: October 16, 2010
Accepted: February 11, 2011
Recommended by subject editor: Pedro Alcântara-Pessôa













