Services on Demand
Journal
Article
Indicators
-
 Cited by SciELO
Cited by SciELO
Related links
-
 Similars in
SciELO
Similars in
SciELO
Share
Latin American applied research
Print version ISSN 0327-0793
Lat. Am. appl. res. vol.42 no.4 Bahía Blanca Oct. 2012
ARTÍCULO
Short term hydrothermal coordination problem considering environmental concerns
A. J. Rubiales, M. A. Risso, F. J. Mayorano and P. A. Lotito
PLADEMA, UNCPBA -CONICET, 7000 Tandil, Argentina {arubiale, risso, fmayoran, plotito}@exa.unicen.edu.ar
Abstract - Solving the Short Term Hydrothermal Coordination Problem considers the resolution of both the Unit Commitment and the Economic Dispatch for thermal and hydraulic units. This problem is solved for several time horizons between a day and a week with a one-hour step. The traditional short-term scheduling problem of hydrothermal units, minimizing fuel cost during a time, does not include concerns due to emission pollution coming from the operation of thermal plants. In this work, environmental constraints are considered. Focusing on avoiding post-dispatch corrections, the transmission network is modeled with a high level of detail considering an AC power fow. These facts lead to a very complex optimization problem which is solved by using a novel decomposition approach based on Generalized Benders Decomposition and traditional, well-known optimization techniques. The approach presented in this work allows the decomposition of the whole problem in a quadratic mixed integer master problem, and in a separable non-linear subproblem. The former defnes the state and the active power dispatched by each unit whereas the latter determines the reactive power to meet the electrical constraints through a modified AC optimal power fow. Diferent variations of the developed methodology were evaluated in order to consider environmental constraints. These approaches were applied to a 9-bus test case and to a 87-bus real system.
Keywords - Short Term Hydrothermal Coordination; Unit Commitment; Generalized Benders Decomposition; Environmental Constraints.
I. INTRODUCTION
Short Term Hydrothermal Coordination Problem (STHTC) considering a centralized dispatch has been used worldwide, especially in Latin-America (Sifuentes and Vargas, 2007a). Solving this problem defnes the operation state and power level of each generation unit (thermal and hydraulic) of an interconnected power system achieving the lower operative cost, satisfying technical and operative constraints of generators and transmission network, among others.
Although the use of clean generation technologies is growing nowadays, fossil fuels represent a reliable and afordable source of energy, necessary to satisfy the demand for electric energy. Economies based on fossil fuels has brought with it the potential harmful problem of the emission of gaseous and particulate products of combustion, which when reaches a prespecifed threshold, is termed pollution (Bellhouse and Whittington, 1996). Environmental concerns are becoming increasingly relevant for companies as regulations on pollutants become more stringent, therefore these concerns must be considered in scheduling models.
Conventional power generation plants causes pollution through the emission of several gases into the atmosphere. Among these gases are carbon dioxide (C02), sulfur dioxide (S02) and nitrogen oxides (N0x) which have a global environmental impact (greenhouse efect) and local efects such as acid rain and reduced visibility among others. In this work, environmental concerns are considered as a cost given by quadratic functions of thermal power generated by each unit. These functions are used to penalize the amount of emission of each gas.
The STHTC problem without considering environmental constraints has been studied considering different formulations and using diferent resolution techniques. The simpler ones, which consider basic models which do not represent real characteristics of electric systems, are the starting point of this research feld. Among the more basic formulations is the one presented in Wood and Wollenberg (1984), which is an academic approach that only considers thermal units and is solved using a merit order list. This means that the units are dispatched in increasing cost order by Megawatt produced. This procedure is quite diferent from the one used in real systems as it does not take into account inter-temporal constraints (such as minimum periods of operation of thermal units or the consideration of start-up costs); or the fact that not always the thermal generation units operate at a constant power level. 0ther techniques, ranging from classical optimization methods, such as dynamic programming, Lagrangean relaxation and methods based on Benders decomposition, to fully heuristic approaches, are presented in literature.
The use of dynamic programming to solve the STHTC problem was also mentioned in Wood and Wollenberg (1984). It provides the possibility of modeling complex objective functions and constraints, and it is both easy to understand and to implement as well as to integrate and to combine with other optimization methods. Although dynamic programming allows modeling non-linear and non-convex problems, because of its combinatorial characteristic (Hillier et al., 1990), to have reasonable calculation times only a small number of thermal units can be considered. This fact makes it impractical for large problems, as is the case of STHTC. In Rubiales et al. (2007), this approach is applied to a hydrothermal system with pumpedstorage units. This article mentions the problem of dimensionality and the approach presented in Lemaréchal and Sagastizábal (1997), is suggested for its resolution.
While the application of Lagrangian relaxation to Economic Dispatch (ED) problems has been done since the mid-nineties, approaches considering network issues can be seen only in the last ten years. For example, 0ngsakul and Petcharaks, shows the numerical solution of the ED and Unit Commitments (UC) problems addressed by a Lagrangian relaxation variation called ILR by Improved Lagrangian Relaxation. It was applied to the IEEE 24-bus test case only considering thermal units and DC network constraints.
Lagrangian relaxation and Benders method are applied in Lu and Shahidehpour (2005), to solve the problem of UC on a set of thermal units considering a detailed network. This algorithm was applied to a case of 118 buses network with a planning horizon of 24 hours. Among more recent works that consider hydroelectric units is Finardi et al. (2005), which combines the use of Lagrangean relaxation with sequential quadratic programming. Although in Finardi et al. (2005), the authors defne a detailed model of hydroelectric plants, network constraints are not considered.
Another approach which uses a combination of augmented Lagrangian relaxation and dynamic programming is presented in Wang et al. (1995). In this work, the decomposition and coordination technique is used for generation scheduling with transmission and environmental constraints. Even though numerical results indicate that the proposed approach is fast and efficient in dealing with numerous system constraints, the network model used does not accurately represent real power networks. Therefore, post-dispatch corrections are necessary.
In recent years, due to the advantages that generalized Benders decomposition (GBD) have shown for the resolution of large scale problems, several papers that address the short-term study using GBD (Geofrion, 1972) have been presented. An algorithm based on this technique is presented in Murillo-Sanchez and Thomas (1998). It considers AC power fows but only thermal power generation. A method based on Benders decomposition to solve the problem of multistage hydrothermal coordination is presented in Diniz et al. (2006). In this representation, the hydroelectric sector is modeled with a high level of detail but applies a linear DC losses model of transmission lines. 0ne of the frst studies that considers the application of GBD to the problem of STHTC considering AC power fows network constraints is Sifuentes and Vargas (2007b). 0ne of the drawbacks mentioned in this work is the slow convergence of the algorithm due to the well known tailing-of efect presented by this resolution scheme.
The approach presented in Catalão et al. (2008), allows short-term scheduling of thermal units, designed to simultaneously address the economic issue of the fuel cost incurred on the commitment of the units and the environmental consideration due to emission allowance trading. In Catalão et al. (2008), the STHTC considering emission constraints is modeled by a multiobjective optimization problem, which is solved by a combination of the weighted sum method with the e-constraining method. However, in Catalão et al. (2008), the authors do not consider network which are necessary to avoid post-dispatch corrections.
Among fully heuristic approaches there are several works that should be mentioned. 0ne of the earliest applications of Genetic Algorithms (GA) to solve the STHTC problem was presented in Chen and Chang (1996). The GA was used to solve the hydro subproblem considering the efects of net head and water travel time delays with a 24 hours planning horizon. A realistic system was employed to test the method and compare its performance to a dynamic programming approach with good results. An overview on GA methods was presented in 0rero and Irving (1998) and applied to determine the optimal short-term scheduling of hydrothermal systems. 0ne of latest application of GA to STHTC was presented in Troncoso et al. (2008) where the on/of status of the thermal and hydro units was computed. The GA was compared to an interior-point method approach and as expected, the GA gave better feasible minima while the interior-point method showed better convergence properties.
Meta-heuristic search algorithms like particle swarm optimization (PS0) are applied to STHTC were presented in Sinha and Lai (2006) and compared to other metaheuristic search algorithms. Comparison revealed that PS0 approach was superior as it proved better convergence characteristics and less solution time. In Yu et al. (2007), diferent PS0 versions were presented, applied to solve STHTC problem and compared to each other. In this work there were four versions of PS0 based on the size of the neighborhood and the formulation of velocity updating. The algorithms were applied to a test system consisting of a number of hydro units and an equivalent thermal unit. Compared to other evolutionary approaches, the different PS0 algorithms showed better performance and in particular, the local versions of the PS0 were found best as they could maintain the diversity of population. A deeper review of heuristic approach applied to STHTC problem is presented in Farhat and ElHawary (2009).
The main contribution in this paper is a method for the solution of a sophisticated version of STHTC that includes enviromental constraints. This version covers both the unit commitment of the units (thermal and hydropower), and the economic dispatch of them. To apply this algorithm to Latin American countries, where systems consist of weakly meshed networks and overloaded lines with power plants located far from major demand points, an AC network modeling is considered. Environmental constraints are included to consider concerns due to emission pollution coming from the operation of thermal plants. 0ther advantages of the present method are that no postdispacth corrections are needed and as it is a non heuristic method a good stopping criterium is available.
II. PROBLEM DEFINITION
In this section the STHTC problem applied to centralized electricity markets based on audited costs is defned. The minimization problem objective function is given by (1). If environmental constraints are not considered, it corresponds to the cost related to produce the electricity needed to meet a fixed demand, which is estimated for each period. Emission control may be included as an extra cost of generation (Ramanathan, 1994) or as an extra constraint which limits the total emission generated by each thermal unit during the planning horizon. In this approach the former methodology is chosen and diferent types of emissions (C02, S02, N0x, etc.) are considered. Like fuel cost curves, the C02, S02 and N0x emission functions can be expressed as quadratic costs for each emission type. The total cost function o summarize costs associated with fuel consumption and start-up of thermal units and penalties related with diferent types of emissions. This function is defned as follows:
 | (1) |
 | (2) |
 | (3) |
Hence, power generation cost Pt,i and pollution generated Eq,t,i for each unit are defned as a quadratic curve. The coefficients Xq,i, Yq,i and Zq,i are generally obtained by curve ftting. The number of terms and segments in the emission curve depends upon the characteristic of the unit (Ramanathan, 1994). It should be mentioned that hydrothermal units does not have costs associated to environmental concerns and to power generation. Environmental costs of hydroelectric units are not present in o because only emission costs are considered. The electricity generated by these units is derived from the force or energy of falling water which is accumulated in unit reservoir and they do not consume any kind of fuel. However, the use of water to generate power hydroelectrically in a given time comprise the use of water for future generation and viceversa. The main issue is to know the total volume of water to be spent in the planning horizon. In the literature, there are two methods for dealing with this issue Wood and Wollenberg (1984). The frst one considers that the total amount of water in the reservoir is available in the short term, but a value to the amount of water that is not spent is assigned to motivate hydroelectric plants to keep water beyond the horizon of analysis. The second approach considers that a known fixed volume of water is available to be used in the planning horizon (obviously, less than the total volume of water in the reservoir) as a result of longterm programming that takes into account other modeling aspects (uncertainty in weather, demand, etc.). In this work, the second approach is adopted, avoiding the need to assign the value of water. This fixed volume of water available during the horizon of analysis is considered in the defnition of the initial and fnal volume for each reservoir.
The constraints were divided into fve groups, which are detailed below.
A. Constraints associated with thermal units only
Equation (4) represents box constraints associated with the active power of each thermal unit:
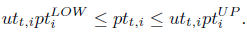 | (4) |
Thus, given the discontinuity the power of a thermal unit has, it is necessary to introduce binaries variables to properly address possible states of operation.
Equation (5) represents box constraints associated with the reactive power of each thermal unit:
 | (5) |
As for active power, binary variables to represent the possible states of operation should be introduced.
In order to determine when a unit is poweredon or powered-off, in (6) a binary stt,i and a continuous ett,i variable (between 0 and 1) are defned. 0nly at this time, they take the value 1 if it corresponds, for any other condition these value is 0. More precisely, stt,i takes the value 1 if the unit i is turned on on period t (0 for other cases). 0n the other hand, ett,i takes the value 1 if the unit i is turned of on period t.
These variables were introduced not only to consider the starting cost of a thermal unit but also to model minimum on and of time of each unit.
 | (6) |
Constraints modeling minimum on and of time of each unit are shown in (7) and (8).
 | (7) |
 | (8) |
Equation (9) defnes ramping constraints for thermal units.
 | (9) |
The maximum amount of fuel available for a thermal unit during planning horizon is considered in (10). In some papers this constraint groups a set of units within a plant.
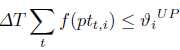 | (10) |
B. Constraints associated with hydro power units only
Equations (11) and (12) represent minimum and maximum active and reactive power output of hydraulic unit generation:
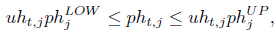 | (11) |
 | (12) |
In order to avoid losing generality, discontinuities in hydraulic units are also considered.
Equation (13) represents the linear relationship between water fow across turbine and the power generated by each hydraulic unit:
 | (13) |
There are several approaches to model this relationship. In those applied to systems mainly served by hydropower, such as Brazil, great importance is given to the accuracy of this relationship (Diniz and Maceira, 2008). In other works, because of the linear nature of the production function for the case of plants with a great fall, the fow variable is eliminated leaving everything in terms of generated power. However, it is preferred to explicitly maintain the variable representing the fow; sometimes these variables are eliminated to make the problem more compact.
C. Constraints associated with both types of generation
Constraint (14) represents the spinning reserve of the whole system for each period:
 | (14) |
Nodal balance of active power for each period is defned in Eq. (15), where Pt,b,b' (16) represents the real part of power fow (active) presented in the line between bus b and b'. The set cb(b) on which the sum is applied, corresponds to the buses directly connected to the bus b.
 | (15) |
where
 | (16) |
Equation (17) defnes the nodal balance of reactive power for each period. Qt,b,b' (18) represents the complex part of power fow (reactive) presented in the line between bus b and b'
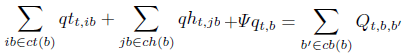 | (17) |
 | (18) |
A deeper explanation about how equations (1518) are obtained goes beyond the scope of this work and is presented in classical books such as (Wood and Wollenberg, 1984) and (Grainger and Stevenson, 1994).
D. Hydraulic related constraints
Reservoir water balance is represented in (19):
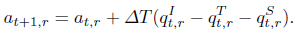 | (19) |
Although only one unit per reservoir is considered, it should be easily extended to several units for the same reservoir. The initial and fnal volume of water of each reservoir is fixed because the total amount of water to consume during the planning horizon is a result of longterm programming, as it was mentioned in the previous section.
Equation (20) represents box constraints to reservoir water volume.
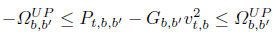 | (20) |
E. Network related constraints
Constraints associated with transmission lines and transformers capacity are defned in (21), while allowed voltage levels for each bus are considered in (22).
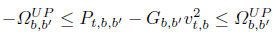 | (21) |
 | (22) |
F. Maintenance of system components
In order to address constraints associated with system elements which are temporarily out of service, or conversely, whose operation is forced for some other reason, the above constraints should be modified. For instance, the availability of thermal or hydraulic units for a given period can be previously defned forcing binaries variables utt,i or uht,j.
III. SOLUTION METHODOLOGY
To simplify the resolution of the problem avoiding falling into infeasible solutions, penalties for being unable to provide active or reactive power to the system are include into the problem formulation. They are represented by variables  ,
,  and
and  .
.
They allows closing the nodal balance (active and/or reactive) for any condition, preventing the occurrence of infeasibility in the optimization problem. If these variables are diferent from zero at the fnal solution then the proposed generating schedule cannot satisfy the active and/or reactive power demand in any bus. Following these considerations, Eqs. (15) and (17) are redefned as (23) and (24) respectively.
 | (23) |
 | (24) |
And the objetive function (1) including deficits and excesses penalizations is redefned as follows:
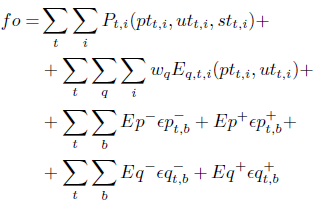 | (25) |
When applied to real cases the scale of the resulting problem formulation is usually large. Therefore, many authors have considered decomposition methods (Baptistella and Geromel, 1980; Pereira and Pinto, 1983; Habibollahzadeh and Bubenko, 1986; Carneiro et al., 1990; Conejo and Medina, 1994; Bai and Shahidehpour, 1996; Demartini et al., 1997; Enamorado et al., 2000; Alguacil and Conejo, 2000; Finardi and da Silva, 2006; Sifuentes and Vargas, 2007b; Norbiato dos Santos and Diniz, 2009; Takigawa et al., 2010).
Among the most utilized decomposition methods there is the Benders method, introduced in 1967 in (Benders, 1962) and generalized in 1972 by Geofrion (7). As any variable partitioning method, this method applies when the problem can be formulated in the form
 | (26) |
and fixing the value of x the resulting problem is an easier solved problem.
Calling f(x) the optimal value of the subproblem
 | (27) |
the original problem can be written in the following form
 | (28) |
where we have considered that f(x) = +8 in the case that there is no y ∈ Y such that g(x, y) ≤ 0.
In most of the practical cases, the optimal value function f is convex and it is easy to compute one subgradient using the Lagrange multipliers associated to the constraints in (27). In those cases it is possible to approximate the function f by a cutting plane model
 | (29) |
where i and ξi are the function value and a subgradients of f for some points xi in X.
In fact, it can be shown that under some hypothesis the function f is equivalent to
 |
Now, the defnition in (29) can be seen as fnite evaluation approximation of this formula, made upon cutting planes that in the convex case are support planes, see Fig. 1 for a graphical example. The interest of this formulation is that subgradients of f are automatically obtained at each evaluation of f; through formula 27.

Figure 1: Evolution of the cutting plane algorithm.
It may happen that the subproblem for some value of x is unfeasible and there are no multipliers to build a cutting plane. In those cases it is possible to include
feasibility cuts, as it is shown in (Bonnans et al. , 2006), however, we will not need these cuts because in our case the subproblem is always feasible.
The Benders method starts with an initial solution x00 ∈ X and obtains the actual value f(x0) solving the subproblem (27). After computing the first k - 1 iterations there is a point xk-1 and a cutting plane approximation fk-1. Then it solves the master problem
 | (30) |
that, considering the formula (29), can be reformulated as
 | (31) |
Calling xk the solution to the master problem, the algorithm keeps iterating until the gap between upper and lower bounds is small enough. The lower bound is given by the solution of the master problem and the upper bound is given by the solution to the subproblem.
B. Decomposed problem
The optimization problem of minimizing the function (1) constrained to (4-22) is written under the following form
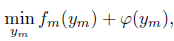 | (32) |
where ym represents the variable of the master problem. The function f is the objective function of the subproblem, the variable of the subproblem is called ysp and fsp(ym, ysp) is the objective function of the subproblem. Now, the constraints must be included in each one of the problems. Different choices will correspond to a different behavior of the Benders algorithm. In this case all the binary variables and the active power variables are considered for the master problem letting all the others variables belong to the subproblem. We have then
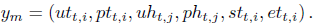 | (33) |
For the masterproblem objective function, we considered the start-up costs of the thermal units toghether with the quadratic terms of the thermal generation costs. Thus, we obtain
 | (34) |
The constraints considered for the master problems are all those that not contain the variables of the subproblem: (4), (611), (13), (14), (19), (20).
Now the subproblem objective function becomes
 | (35) |
Toghether with the variables that appear in this function, the subproblem has also the reactive power variables qtt,i , qht,j the corresponding slack variables 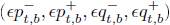 , the angles ?t,b and the voltages ?t,b. The remaining constraints (5), (12), (15), (17), (21), (22) are considered in the subproblem with the values of master variables fixed by the master problem.
, the angles ?t,b and the voltages ?t,b. The remaining constraints (5), (12), (15), (17), (21), (22) are considered in the subproblem with the values of master variables fixed by the master problem.
With the proposed decomposition the resulting master problem is numerically more complex than the subproblem. Indeed, it is a quadractic mixed integer problem. The subproblem has a linear objective function and non linear constrains, but the non linearity of the constraints is non harmful in practice and the solvers used can deal well with them.
It is worth mentioning also that the subproblem becomes temporally uncoupled obtaining several optimal fow problems where the values of the start-up variables utt,i, uht,j and the active power generation ptt,i, pht,j are given by the master problem solution at each iteration. In order to simplify the introduction of cutting plane equations some dummy equations were added:
 | (36) |
where uht,j , pht,j , utt,i y ptt,i are now subproblem variables,  ,
,  y
y  y
y  are given by the master problem at the k iteration and
are given by the master problem at the k iteration and  ,
,  ,
,  ,
,  are the corresponding multipliers.
are the corresponding multipliers.
The addition of cutting planes to the master problem is made in the same way that in (30) and (31). The master objective function has the term Σt zt which corresponds with f(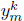 ), and the cutting planes are:
), and the cutting planes are:
 |
IV. RESULTS
In this section the main results obtained by applying the proposed approach are presented. The application of the previously detailed algorithm are performed on systems of different sizes. Initially, a fctional nine buses system presented in (Sifuentes and Vargas, 2007a) is considered. Result details which are diffcult to observe in larger systems can be considered in this small example. Additionally, an application of the proposed methodology to a larger real power system is presented. 0ne of the features which should be observed in this section is the ability of the algorithm to consider the reactive power fow and see how this fact impacts in the result. This is an important feature appreciated by system operators because no post dispatch correction should be necessary. Voltage values at each bus are compared with results obtained from PowerWorld Simulator (0verbye et al., 1995; 0verbye and Weber, 2000), which is a standard within the electrical industry. Because this commercial software does not have the ability of solving the hydrothermal coordination problem, power levels for each unit are fixed with algorithm results, and voltage levels in each bus are compared with PowerWorld Simulator values verifying its correctness.
For the sake of clarity, all the technical details of the example networks are given after the bibliography.
A. Nine buses test case
This system is based on a transmission network of 9 buses with 9 lines. The generating equipment consists of three thermal units and an hydroelectric one. The objectives of the tests performed on this system are:
- Analyze the impact of considering environmental constraints.
- Compare bus voltage values with PowerWorld Simulator results.
- Analyze algorithm convergence issues.
In Fig. 2 an one-line diagram of the 9-bus power system is presented. The Table 1, placed after the bibliography, details parameters like resistance (R), reactance (X) and capacity.

Figure 2: 9-bus system one-line diagram.
Table 1: Power lines Characteristics 
Costs, minimum and maximum power generation, maximum active power difference for two consecutive periods and environmental coefficients for each unit are described in Tables 2, 3 and 4.
Table 2: Thermal units power parameters 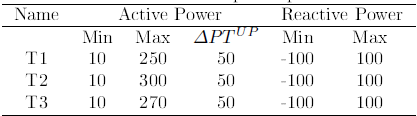
Table 3: Thermal unit costs 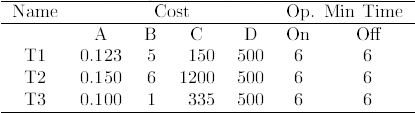
Table 4: Environmental Constraint Coeficients Name X Y Z 
Hydrothermal unit (H1) and its reservoir characteristics are enumerated in table 5 and 6 respectively. For the sake of simplicity, the relation between power generated and water fow rate is modeled by a linear factor βj = 3.846 MW / m3 / s.
Table 5: Hydroelectric Unit Power characteristic Name Act Power [MWh] React Power [MWh] 
Table 6: Reservoir Characteristics 
Table 7 describes the system demand and Spinning Reserve (ζt ) during the whole day. It should be mentioned that the spinning reserve is calculated as 15% of the total demand in each period.
Table 7: Active and Reactive power demand 
Penalty coefficient Ep- , Ep+ , Eq- and Eq+ are defned as 1e6 for this example. It should be mentioned that because in this example there are not fuel consumption constraints, Eq. (10) is not considered.
A.l. Convergence Analysis
In this section a brief analysis of the algorithm convergence considering and without considering environmental constraints is done. In Fig. 3 convergence of both approaches are compared. The gray lines correspond to lower and upper bounds of the algorithm only considering costs. 0n the other hand, the black lines show lower and upper bounds of the algorithm considering environmental concerns.
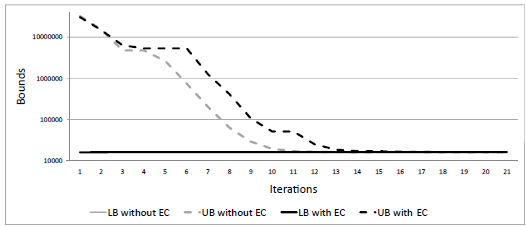
Figure 3: Convergence Analysis
Numerical experiments were performed on a PC AMD Athlon 2.96 GHz X3 435 with 4 GB of RAM. GAMS version used is 23.6 and the solvers used are CPLEX and C0N0PT. Both solvers, interfaced with GAMS, are well known standards and used for many researchers (see Dondo and Cerdá (2006) and Mussati et al. (2006)).
The resolution time for the NonEnvironmental case is 27 seconds and 17 iterations while the Environmental one is 64 seconds and 25 iterations with a relative tolerance of 1e-5. The size of the master model solved consists of 385 variables (and 144 discrete variables). The number of equations starts at 1064 growing to 1640 on iteration number 25. This size growth corresponds to the Benders cuts added in each iteration. 0ne cut is added for each time. The subproblem is decomposed in 24 problems (each one corresponds to a given time interval), with 66 variables and 88 equations each one. It should be mentioned, that for minor relative tolerance values the same solution is reached. Furthermore, values concerning deficits or surpluses of active or reactive power are less than 1e-3 MW, which are negligible in electric power systems. Remarkably, over different runs, these values dramatically impacts on method convergence. Because they are heavily penalized (for the algorithm to avoid network misconfgurations) small changes in these greatly infuence the objective function. These changes do not impact in thermal or hydro power schedule. Therefore, one possible implementation of the stopping criterion, it should be consider a greater tolerance for the difference between upper and lower bounds (1e-1) considering that values of excesses and deficits in each bus are less than a given value. The number of iterations applying this stopping criterion where 17 for the Environmental case and 12 for the other one, drastically reducing the 25 and 17 previously obtained. The solution obtained using the new approach is feasible and the difference in cost between both approaches is less than 0.05%.
A.2. Voltage values comparison with PowerWorld Simulator results
This section was developed in order to verify the correctness of voltage values results. In table 8 bus voltages obtained by applying the proposed algorithm and those calculated by PowerWorld Simulator are displayed. As it was mentioned, this application does not have the option of solving hydrothermal coordination problem considering AC power fow. To compare voltage results for a given time, demand profles and power generated for each unit are fixed with algorithm results.
Table 8: Differences beetween the proposed algorithm and Powerworld Simulator for time=24 
By comparing the values obtained using both approaches the error is never greater than 1 %. In Table 8 bus voltages obtained for t = 24 are displayed.
A.3. Impact of considering environmental constraints
Figure 4 shows thermal and hydraulic units dispatch without considering environmental constraints. Unit T3 and T1 are the units selected by the algorithm to satisfy system demand during the whole horizon. As it can be seen in Table 3, Unit T3 is the cheapest one while Unit T2 is the most expensive one considering operative cost. Conversely, Unit T2 is is the more effcient one considering environmental aspects and T3 is the more pollutant thermal unit. Figure 5 shows thermal and hydraulic units dispatch considering environmental concerns. Although in real cases there is no such a big difference in the dispatch strategy considering environmental aspects, in this case, a high value of wq = 1.2 is selected in order to emphasize differences between both approaches. When environmental concerns are considered Unit T2 is turned on during the whole horizon as shown in Fig. 5.

Figure 4: Power Generation without considering Environmental concerns

Figure 5: Power Generation considering Environmental concerns
B. Midsize real power system
The proposed algorithm was also applied to a section of the Argentinean National Interconnected System which is operated by Transcomahue. This network is located in the Upper Valley zone and includes the provinces of Neuquen and Rio Negro. The extension of this power network is considered of medium size and has thermal and hydraulic generation. The network modeled considers the 132 kV voltage level areas and lower voltage buses and lines that reach the generators. The system demands are considered as bus connections which consumes power at 132 kV.
This system has 87 buses, 23 thermal and 6 hydraulic units. The one-line diagram is presented in Fig. 6, in order to have an idea of the network topology.

Figure 6: Midsize real power network
Table 10: Thermal Units Power Characteristics 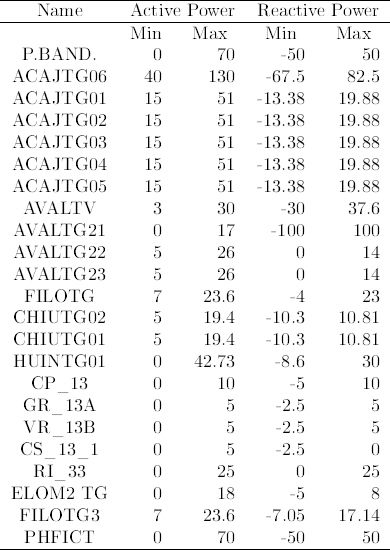
Hydraulic units characteristics are shown in table 9.
Table 9: Hydraulic Units Power Characteristics 
As cost coefficients, data from the reservoirs were not provided; consequently, fictitious values are considered. For the sake of simplicity, characteristics of is located in the Upper Valley zone and includes the lines, thermal costs and environmental concerns are not shown.
As with previous case, numerical experiments were performed on a PC AMD Athlon 2.96 GHz X3 435 with 4 GB of RAM. GAMS version used is 23.6 and the solver used for solving the problem are CPLEX and CONOPT. The resolution time for the Non-Environmental case is 544 seconds and 51 iterations while the Environmental one is 465 seconds and 44 iterations with a relative tolerance of 1e-3. For this case, the size of the master model solved consist of 2665 variables (and 1104 discrete variables). The number of equations start at 7789 growing to 8821 on iteration number 44. This size growth corresponds to the Benders cuts added in each iteration. One cut is added for each time. The subproblem is decomposed in 24 problems (each one corresponds to a given time interval), with 601 variables and 815 equations each one.
V. Conclusion
In this work, an AC detailed version of the STHTC considering environmental concerns was mathematically formulated. The solution of this problem defnes the unitcommitment and economical dispatch of thermal and hydraulic unit avoiding post-dispatch corrections. This formulation of the AC transmission network makes the optimization problem to be solved a mixed-integer nonconvex and large scale optimization problem.
The model was formulated in such a way that the results can be applied to systems with large and weakly meshed networks, typical of underdeveloped or developing countries with large territories, such as those in Latin America. This formulation integrates the hydrothermal coordination problem with the resolution of optimal power fow for each period.
The approach applied in this work consist in splitting the original problem in a non-linear master problem with mixed integer binary variables and a non-linear subproblem with continuous variables. The mechanism applied to separate it is the most appropriated one for the type of systems in which the methodology was tested. For the resolution, an approach based on Benders algorithm was applied.
The originality in this work relies in the addition of environmental constraints in the form of penalizing costs. It was shown that the most recent numerical approaches to the solution of the STHTC problem can be modified to include them. It was also shown that the introduction of these constraints can modify substantially the solution.
The results were tested on an academic example already treated by other authors for the sake of comparison, and on a real mid sized network, obtaining in both cases very good numerical performances. It is also noted that the numerical performance can be even improved considering strategies that palliate the tailing of efect of methods based on the cutting plane methodology.
NOMENCLATURE
Sets
| t ∈ T | time periods associated with the planning horizon |
| i ∈ I | thermal units. |
| j ∈ J | thermal units. |
| b, b' ∈ ? | system buses. |
| Ct(b) | thermal units directly connected to bus b. |
| Ch(b) | hydroelectric units directly connected to bus b. |
| Cb(b) | buses directly connected to bus b. |
| r ∈ R ) | reservoirs or dams. |
| q ∈ Q ) | emission types.b. |
Variables
| ptt,i, pht,i | active power generated by thermal (hydroelectric) unit i for period t. |
| utt,i | binary variable indicating the state of the thermal unit i for period t. |
| stt,i | binary variable indicating that the thermal unit i has started for period t. |
| ett,i | continuous variable that is used for the purpose of checking that the minimum and maximum time of operation of each thermal unit is accomplished. |
| qtt,i, qht,i | reactive power generated by thermal (hydroelectric) unit i for period t. |
 , ,  | active power deficit and excess on bus b for period t. |
 , ,  | reactive power deficit and excess on bus b for period t. |
| at,r | water volume of the reservoir r for period t. |
 | across-turbine outfow of the reservoir r for period t. |
 | spilled outfow of reservoir r for period t. |
| ?t,b | voltage on bus b for period t. |
| ?t,b | voltage angle for period t on bus b. |
| t,bb' | real part of power fow (active) presented in the line between bus b and b'. |
| Pt,bb' | real part of power fow (active) presented in the line between bus b and b'. |
| Qt,bb' | complex part of power fow (reactive) presented in the line between bus b and b'. |
Parameters
| Ai, Bi, Ci | quadratic, linear and free cost coefficient of thermal unit i. |
| Di | start-up cost coefficient of thermal unit i. |
| Xq,i, Yq,i, Zq,i | quadratic, linear and free coefficient of the emission curve of thermal unit i for emission type q. |
| Ep-, Ep+ | penalty coefficient due to active power deficit and excess. |
| Eq-, Eq+ | penalty coefficient due to active power deficit and excess. |
 , ,  | minimum and maximum active power output of thermal unit i. |
 , ,  | minimum and maximum reactive power output of thermal unit i. |
 , ,  | minimum and maximum active power output of hydroelectric unit j. |
 , , 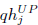 | minimum and maximum reactive power output of hydroelectric unit j. |
 , , | minimum ontime of thermal unit i. |
 , , | minimum off-time of thermal unit i. |
 , , | maximum active power diference for two consecutive periods of unit i. |
 , , | maximum fuel for unit i for whole planning horizon. |
| ζt | spinning reserve required for period t. |
| Ψpt,b, Ψqt,b | active and reactive power load for period t on bus b. |
| Gb,b' , Bb,b' | real and complex components of the admittance matrix for the line b → b'. |
 , ,  | minimum and maximum volume limits of reservoir r. |
 , , | infow of reservoir r for period t. |
 , , 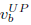 | minimum and maximum voltage limits of bus b. |
 , , | power fow limit between buses b and b'. |
| Oq | emission to cost conversion factor for emission type q. |
| βj | linear coefficient of the relationship between water fow across turbine and the power generated by each hydraulic unit j. |
For the sake of clarity we omitted to mention the domain of the indexes in formulas and equations. If not stated otherwise, they should be considered for each possible value of each index in the corresponding domain set.
References
1. Alguacil, N. and A.J. Conejo, "Multiperiod optimal power fow using benders decomposition," IEEE Transactions on Power Systems, 15, 196-201 (2000). [ Links ]
2. Bai, X. and S.M. Shahidehpour, "Hydrothermal, scheduling by tabu search and decomposition method," IEEE Transactions on Power Systems, 11, 968-974 (1996). [ Links ]
3. Baptistella, L.F.B. and J.C. Geromel, "Decomposition approach to problem of unit commitment schedule for hydrothermal systems," IEE Proceedings D Control Theory and Applications, 127, 250-258 (1980). [ Links ]
4. Bellhouse, G.M. and H.W. Whittington, "Simulation of gaseous emissions from electricity generating plant," International Journal of Electrical Power f Energy Systems, 18, 501-507 (1996). [ Links ]
5. Benders, J. "Partitioning procedures for solving mixedvariables programming problems," Numerische Mathematik, 4, 238-252 (1962). [ Links ]
6. Bonnans, J.F., J.C. Gilbert, C. Lemaréchal and C.A. Sagastizábal, Numerical Optimization: Theoretical and Practical Aspects, Springer-Verlag, Berlin, Germany (2006). [ Links ]
7. Carneiro, A.A.F.M., S. Soares and P.S. Bond, "A large scale of an optimal deterministic hydrothermal scheduling algorithm," IEEE Transactions on Power Systems, 5, 204-211 (1990). [ Links ]
8. Catalão, J., S. Mariano, V. Mendes and L. Ferreira, "Shortterm scheduling of thermal units: emission constraints and tradeof curves," European Transactions on Electrical Power, 18, 1-14 (2008). [ Links ]
9. Chen, P. and H. Chang, "Genetic aided scheduling of hydraulically coupled plants in hydrothermal coordination," IEEE Transactions on Power Systems, 11, 975-981 (1996). [ Links ]
10. Conejo, A. and J. Medina, "Longterm hydrothermal coordination via hydro and thermal subsystem decomposition," Proc. th Mediterranean Electrotechnical Conf., 921-924 (1994). [ Links ]
11. Demartini, G., T.R. De Simone, G.P. Granelli, M. Montagna and K. Robo, "Dual programming methods for largescale thermal generation scheduling," Proc. 20th Int Power Industry Computer Applications. Conf. (1997). [ Links ]
12. Diniz, A.L. and M.E.P. Maceira, "A fourdimensional model of hydro generation for the short-term hydrothermal dispatch problem considering head and spillage efects," IEEE Transactions on Power Systems, 23, 1298-1308 (2008). [ Links ]
13. Diniz, A.L., T.N. Santos and M.E.P. Maceira, "Short term security constrained hydrothermal scheduling considering transmission losses," Proc. IEEE/PES Transmission f Distribution Conf. and Exposition: Latin America TDC '06, 1-6 (2006). doi:10.1109/ TDCLA.2006.311437. [ Links ]
14. Dondo, R. and J. Cerdá, "An MILP framework for dynamic vehicle routing problems with time windows," Latin American applied research, 36, 255-261 (2006). [ Links ]
15. Enamorado, J.C., A. Ramos and T. Gomez, "Multiarea decentralized optimal hydrothermal coordination by the dantzigwolfe decomposition method," Proc. IEEE Power Engineering Society Summer Meeting, 4, 2027-2032 (2000). [ Links ]
16. Farhat I. and ElHawary M. 0ptimization methods applied for solving the short-term hydrothermal coordination problem. Electric Power Systems Research, 79 (9):1308-1320, 2009. [ Links ]
17. Finardi, E., E. da Silva and C. Sagastizábal, "Solving the unit commitment problem of hydropower plants via Lagrangian Relaxation and Sequential Quadratic Programming," Computational & applied mathematics, 24, 317-342 (2005). [ Links ]
18. Finardi, E.C. and E.L. da Silva, "Solving the hydro unit commitment problem via dual decomposition and sequential quadratic programming," IEEE Transactions on Power Systems, 21, 835-844 (2006). [ Links ]
19. Geofrion, A., "Generalized benders decomposition," Journal of optimization theory and applications, 10, 237-260 (1972). [ Links ]
20. Grainger, J. and W. Stevenson, Power system analysis, 152, McGrawHill New York (1994). [ Links ]
21. Habibollahzadeh, H. and J.A. Bubenko, "Application of decomposition techniques to short-term operation planning of hydrothermal power system," IEEE Power Eng. Rev., 6, 28-29 (1986). [ Links ]
22. Hillier, F., G. Lieberman and G. Liberman, Introduction to operations research. McGrawHill New York (1990). [ Links ]
23. Lemaréchal, C. and C. Sagastizábal, "Variable metric bundle methods: from conceptual to implementable forms," Mathematical Programming, 76, 393-410 (1997). [ Links ]
24. Lu, B. and M. Shahidehpour, "Unit commitment with fexible generating units," IEEE Transactions on Power Systems, 20, 1022-1034 (2005). [ Links ]
25. Murillo Sanchez, C. and R. Thomas, "Thermal unit commitment including optimal AC power fow constraints," Proceedings of the Hawaii International Conference on System Sciences, IEEE Institute of Electrical and Electronics, 31, 81-88 (1998). [ Links ]
26. Mussati, S.F., P.A. Aguirre and N.J. Scenna, "Thermodynamic approach for optimal design of heat and power plants: Relationships between thermodynamic and economics solutions," Latin American applied research, 36, 329-335 (2006). [ Links ]
27. Norbiato dos Santos, T. and A.L. Diniz, "A new multiperiod stage defnition for the multistage benders decomposition approach applied to hydrothermal scheduling," IEEE Transactions on Power Systems, 24, 1383-1392 (2009). [ Links ]
28. 0ngsakul, W. and N. Petcharaks, "Transmission constrained generation scheduling in a centralized electricity market by improved Lagrangian relaxation," IEEE Power Engineering Society General Meeting, 1156-1163 (2005). [ Links ]
29. 0rero, S. and M. Irving, "A genetic algorithm modelling framework and solution technique for short term optimal hydrothermal scheduling," IEEE Transactions on Power Systems, 13, 501-518 (1998). [ Links ]
30. 0verbye, T., P. Sauer, C. Marzinzik and G. Gross, "A userfriendly simulation program for teaching power system operations," IEEE Transactions on Power Systems, 10, 1725-1733 (1995). [ Links ]
31. Overbye, T. and J. Weber, "Visualization of power system data," Proceedings of the 33rd Annual Hawaii International Conference on System Sciences (2000). [ Links ]
32. Pereira, M.V.F. and L.M.V.G. Pinto, "Application of decomposition techniques to the mid and short term scheduling of hydrothermal systems," IEEE Trans. Power App. Syst., 102, 3611-3618 (1983). [ Links ]
33. Ramanathan, R., "Emission constrained economic dispatch," IEEE Transactions on Power Systems, 9, 1994-2000 (1994). [ Links ]
34. Rubiales, A., F. Mayorano and P. Lotito, "0ptimización aplicada a la coordinación hidrotérmica del mercado eléctrico argentino," Mecánica Computacional, 26, 1906-1920 (2007). [ Links ]
35. Sifuentes, W. and A. Vargas, "Shortterm hydrothermal coordination considering an ac network modeling," International Journal of Electrical Power f Energy Systems, 29, 488-496 (2007a). [ Links ]
36. Sifuentes, W.S. and A. Vargas, "Hydrothermal scheduling using benders decomposition: Accelerating techniques," IEEE Transactions on Power Systems, 22, 1351-1359 (2007b). [ Links ]
37. Sinha, N. and L. Lai, "Meta heuristic search algorithms for short-term hydrothermal scheduling," International Conference on Machine Learning and Cybernetics, 4050-4056 (2006). [ Links ]
38. Takigawa, F.Y.K., E.C. Finardi and E.L. da Silva, "A decomposition strategy to solve the short-term hydrothermal scheduling based on lagrangian relaxation," Proc. IEEE/PES Transmission and Distribution Conf. and Exposition: Latin America (TfD-LA), 681-688 (2010). [ Links ]
39. Troncoso, A., J. Riquelme, J. Aguilar-Ruiz and J. Riquelme Santos, "Evolutionary techniques applied to the optimal short-term scheduling of the electrical energy production," European Journal of Operational Research, 185, 1114-1127 (2008). [ Links ]
40. Wang, S.J., S.M. Shahidehpour, D.S. Kirschen, S. Mokhtari and G.D. Irisarri, "Shortterm generation scheduling with transmission and environmental constraints using an augmented lagrangian relaxation," IEEE Transactions on Power Systems, 10, 1294-1301 (1995). [ Links ]
41. Wood, A. and B. Wollenberg, Power generation, operation, and control, Wiley New York (1984). [ Links ]
42. Yu, B., X. Yuan and J. Wang, "Shortterm hydrothermal scheduling using particle swarm optimization method," Energy Conversion and Management, 48, 1902-1908 (2007). [ Links ]
Received: September 20, 2011
Accepted: March 14, 2012
Recommended by Subject Editor: Mariano Martín Martín














